Савина Н.В. Применение теории вероятности и методов оптимизации в системах электроснабжения
Подождите немного. Документ загружается.

91
возможных значений величины относительно среднего, степень асимметрии,
степень плосковершинности или крутости плотности распределения.
Такие характеристики, назначение которых выразить в сжатой форме
наиболее существенные особенности распределения случайной величины,
называются ее числовыми характеристиками. Таким образом, к числовым
характеристикам относятся: математическое ожидание (среднее значение),
дисперсия, среднеквадратическое отклонение и моменты более высоких
порядков.
Случайная величина может принимать различные значения, поэтому
важно знать её среднее значение. Начальный момент первого порядка – это
среднее значение случайной величины или её математическое ожидание, т.к.
можно ожидать, что вокруг него будут группироваться возможные значения
случайной величины. Операцию осреднения обозначают: М
[
]
х
, или чертой над
обозначением случайной величины
x
, или
c
x .
Рассмотрим, как определяется математическое ожидание для разных
типов случайной величины.
1) Дискретная случайная величина.
Пусть случайная величина Х имеет возможные значения
n
xxxx ...,,
321
с
вероятностями
n
ppp ...,
21
, тогда:
∑
∑
=
=
=
+++
+++
=
n
i
i
n
i
ii
n
nn
p
px
ppp
pxpxpx
xM
1
1
21
2211
...
...
][ . (47)
Учитывая, что
1
1
n
i
i
p
=
=
∑
, получим:
∑
=
=
n
i
ii
pxxM
1
][ . (48)
Таким образом, математическим ожиданием дискретной случайной
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

92
величины называется сумма произведений всех возможных ее значений на
вероятности этих значений.
Пример. Для схемы, приведенной на рис. 45, определить математическое
ожидание дефицита мощности.
Рис. 45
Под дефицитом мощности понимают разность между требуемой
мощностью и пропускной способностью схемы.
Рассмотрим возможные дефициты мощности.
При отключении одного из элементов I группы дефицит мощности
составит 40 МВт, одного из элементов II группы – 20 МВт, при полном
перерыве электроснабжения – 100 МВт. Таким образом, возможные значения
случайной величины дефицита мощности соответственно равны 20; 40; 100
МВт.
Определим вероятности их появления с помощью теорем вероятностей
сложных событий:
(
)
( )
( )
22
122122
2
11222
22
12
2022;
402(2);
100.
деф
деф
деф
ррррq ррq
рррqррq
рр qq
==⋅=
==+
==+
Тогда математическое ожидание дефицита мощности в рассматриваемой
схеме будет равно
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

93
( )
( ) ( ) ( )
( ) ( )
1
2222
1221122212
20204040100100
40802100.
n
деф ii дефдефдеф
i
Мр Ppppррррр
ррq рq ррqqq
=
===+=+==
=++++
∑
2) Непрерывная случайная величина
[]
() ()
Мххfхdx хF х dx
+∞+∞
−∞−∞
==
∫∫
. (49)
3) Смешанная случайная величина
1
[]()
n
n
ii
i
х
Mxxpxfxdx
∞
=
=+
∑
∫
. (50)
Здесь первое слагаемое распространяется на дискретные значения
случайной величины, второе – на непрерывные.
Свойства математического ожидания
1) Математическое ожидание постоянной величины С равно этой
величине С:
CCM
=
][ .
2) Математическое ожидание произведения случайной величины на
постоянную С равно произведению постоянной С на математическое ожидание
случайной величин:
][][ xCMCXM
=
.
3) Математическое ожидание суммы случайной величины равно сумме
математических ожиданий каждой из них:
][][][ bMaMbaM
+
=
+
.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

94
4) Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий:
][][][ bMaMabM
=
.
Математическое ожидание случайной величины характеризует
действительное ее среднее значение, однако этого недостаточно для её полной
характеристики. Необходимо знать насколько отклоняется случайная величина
от своего математического ожидания.
Если эти отклонения невелики, то математическое ожидание достаточно
хорошо представляет случайную величину. Если же отклонения велики, то есть
разброс значений случайной величины (или рассеяние) велико, то одно
математическое ожидание уже не характеризует случайную величину
существенным образом. Для этого вводится вторая числовая характеристика –
дисперсия.
Дисперсия случайной величины характеризует разброс ее значений
относительно математического ожидания.
Нельзя определить степень отклонения случайной величины от её
математического ожидания по среднему значению отклонения, т.к. эта
величина равна 0:
[[]][][]0
MXMXMXMX
−=−=
,
т.к. функция ][XM постоянна. Это объясняется тем, что математическое
ожидание является как бы центром всех значений случайной величины, и
отклонения одного знака компенсируют отклонения другого знака. Поэтому в
качестве меры отклонений случайной величины от её математического
ожидания принимают величину, равную математическому ожиданию квадрата
отклонения случайной величины от её математического отклонения -
дисперсию случайной величины ][xD :
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

95
2
]][[][ XMXMxD −= , (51)
Дисперсия - это центральный момент второго порядка – квадрат
эффективного или среднеквадратического значения отклонения случайной
величины от ее математического ожидания.
Посмотрим как определяется дисперсия для случайной величины разных
типов
1) Дискретная случайная величина:
∑
−=
n
nn
pxMxxD
2
)]([][
, (52)
где суммирование распространяется на все значения случайной величины
n
x ,
имеющие соответствующие вероятности
n
p
.
Дисперсия дискретной случайной величины равна сумме произведений
квадратов отклонений случайной величины от математического ожидания на
их вероятности.
2) Непрерывная случайная величина:
2222
[]()()[[]]()[][]
c
DXxxfxdxXMXfxdxMxMX
+∞+∞
−∞−∞
=−=−=−
∫∫
. (53)
3) Смешанная случайная величина:
22
1
[]()()()
n
n
cic
i
х
DXxxpxxfxdx
+∞
=
=−+−
∑
∫
. (54)
Свойства дисперсии
1) Дисперсия постоянной величины С равна 0:
[]0
D
С
=
.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
96
2) Дисперсия произведения постоянной величины С на случайную
величину Х равна произведению квадрата постоянной величины на дисперсию
случайной:
][][
2
XDCCXD = . (55)
3) Дисперсия суммы независимых случайных величин
a
и
b
равна сумме
дисперсий этих величин:
][][][ bDaDbaD
+
=
+
. (56)
4) Дисперсия суммы постоянной и случайной величины равна дисперсии
случайной величины:
[][]
DcxD
х
+=
. (57)
5) Дисперсия среднеарифметического от ряда
n
случайных величин с
одинаковой дисперсией в
n
раз меньше дисперсии каждой из этих величин в
отдельности:
[ ]
12
12
2
()
...1
()()...()
j
n
n
D
DDDD
nnn
η
ηηη
ηηη
+++
=+++=
. (58)
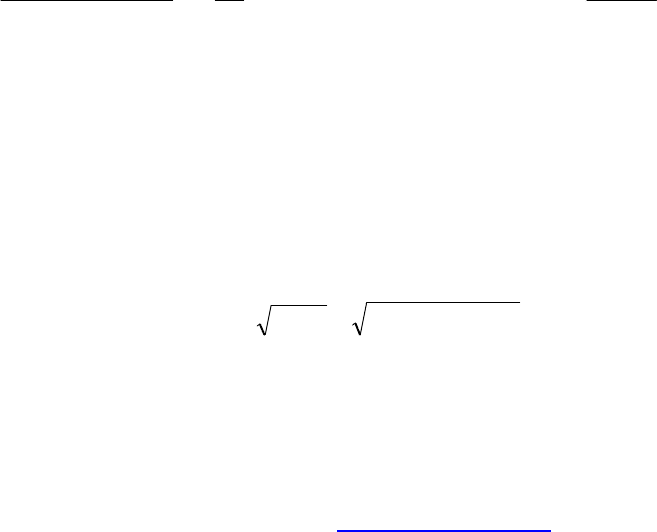
Размерность дисперсии - квадрат случайной величины. В практических
задачах это неудобно. Поэтому ввели понятие среднеквадратического или
стандартного отклонения случайной величины:
2
]][[][)( XMXMXDX −==σ . (59)
Одной из важнейших характеристик является коэффициент вариации –
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

97
это безразмерная величина, использующаяся для сравнения степени изменения
случайной величины относительно математического ожидания:
[]
[]
M
ση
γ
η
=
. (60)
Итак, мы рассмотрели математическое ожидание, дисперсию. Эти
характеристики являются важнейшими и при известном законе распределения
полностью характеризуют случайную величину.
Однако на практике часто приходится встречаться с другими
характеристиками случайных величин. Рассмотрим их.
Моментом
n
-го порядка случайной величины называется математическое
ожидание
n
-ой степени её отклонения от некоторой постоянной
C
, т.е.
[]
n
n
MMC
η=−. (61)
Если
0
=
C
, то момент называется начальным, если
[]
С M
η
=
то момент
называется центральным.
Случайные величины, получаемые вычитанием из текущих значений
x
их среднего значения )(
c
xx − , называются центрированными. Вот они и
характеризуются центральными моментами.
Мы рассмотрели начальный момент первого порядка - математическое
ожидание, центральный момент второго порядка - дисперсию.
Действительно,
)()0()(
1
ηηη MMM =−= ;
2
)]([)( ηηη MDD −= .
Кроме этих моментов, практический интерес представляют центральные
моменты 3 и 4 порядков.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
98
Центральный момент 3 порядка равен
3
3
)]([ ηη MMM −= . (62)
Он имеет размерность куба размерности случайной величины. Чтобы
получить безразмерную величину, его делят на )(
3
ησ . Эта величина называется
коэффициентом асимметрии или асимметрией:
3
3
33
[()]
[][]
к
MMM
S
ηη
σηση
−
== . (63)
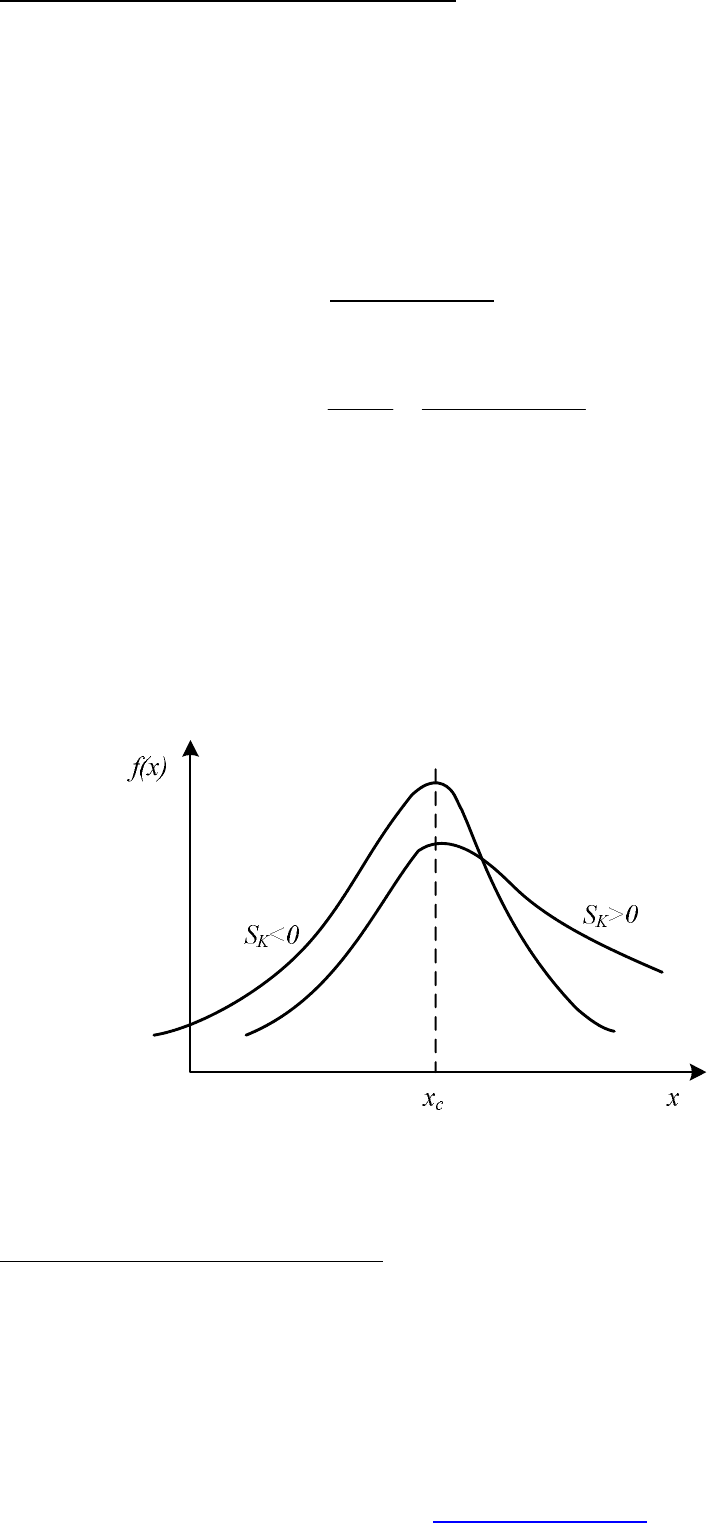
Если кривая плотности распределения вероятностей симметрична
относительно математического ожидания, то
3
M и
0
к
S
=
. Если кривая смещена
влево от математического ожидания, то
0
k
S
<
, если вправо - 0>
k
S .
Рис. 46
Центральный момент 4 порядка – служит для характеристики «крутости»,
т.е. островершинности или плосковершинности плотности распределения
вероятностей по сравнению с кривой нормального распределения. Крутость
характеризуется так называемым эксцессом.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
99
Эксцесс – коэффициент, характеризующий остро- и плосковершинность
кривой плотности распределения вероятностей.
Он равен:
3
)(
)]([
3
)(
4
4
4
4
−
−
=−=
ησ
ηη
ησ
MM
M
E
x
. (64)
Здесь 3 вычитается из отношений
4
M
к
4
σ , чтобы сравнить эксцесс
рассматриваемой плотности распределения с кривой плотности распределения
нормального закона, для которого 3
4
4
=
σ
M
.
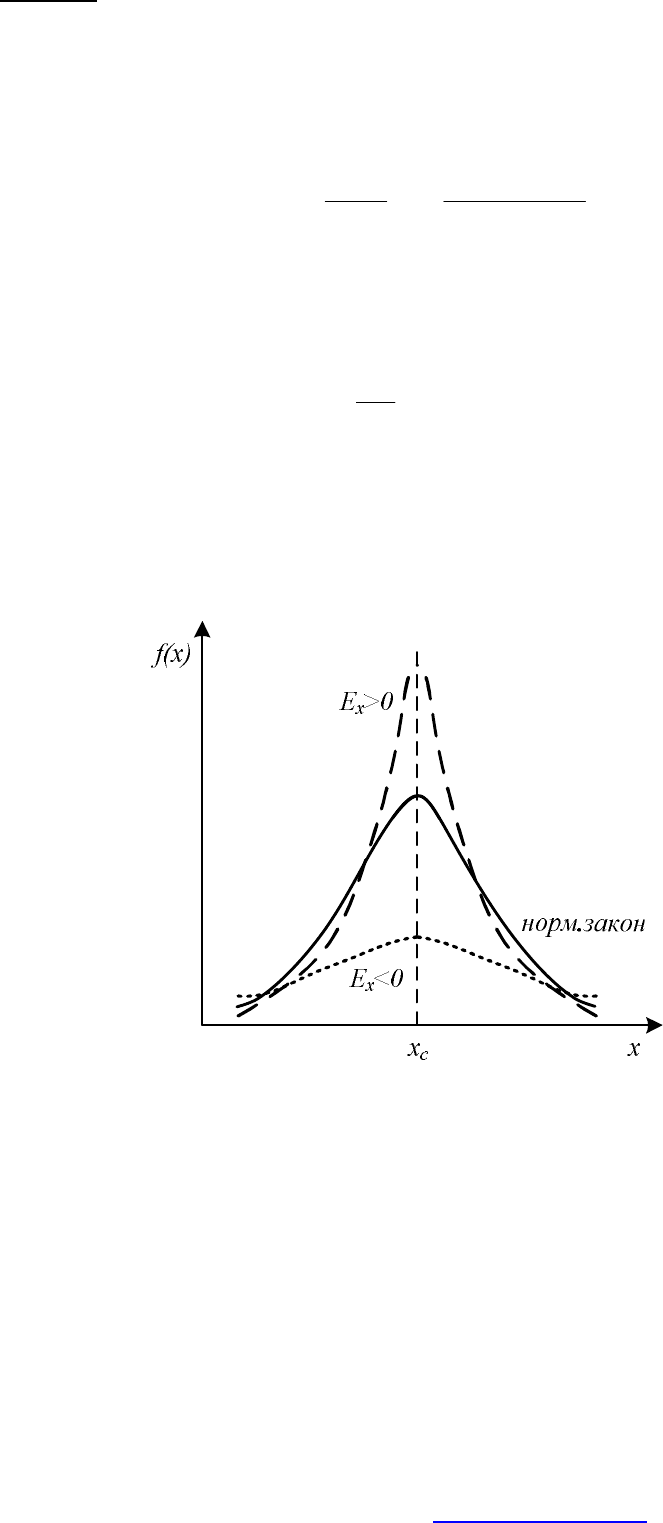
Если 0<
x
E , то распределение имеет более плоскую вершину, чем
нормальный закон и наоборот:
Рис. 47
Таким образом, мы рассмотрели наиболее важные числовые
характеристики для систем электроснабжения.
Теперь, имея представление о них, подробнее рассмотрим виды
плотностей распределения вероятностей случайных величин.
В электроэнергетике рассматриваются случайные величины, которые
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

100
имеют следующие законы распределения: равномерное, простейшее
нормальное, общее нормальное, экспоненциальное, статистический А-ряд
Шарлье – для непрерывных случайных величин и биноминальное, Пуассона –
для дискретных случайных величин.
2.4. Законы распределения вероятностей случайных величин
Равномерное распределение
Величина, имеющая неизменную плотность вероятности, называется
равномерно распределённой непрерывной случайной величиной.
Погрешности измерения параметров режима, погрешности
технологических параметров оборудования, фазы высших гармоник тока и
напряжения, показатели качества электроэнергии и др. могут описываться
равномерным распределением.
Равномерным называется распределение вероятностей случайной
величины Х, если на интервале
(
)
,
ab
, которому принадлежат все возможные
значения
X
, дифференциальная функция постоянна:
constxf
=
)( .
Вне этого интервала 0)(
=
xf
Если непрерывная случайная величина равномерно распределена только в
интервале
(
)
,
ab
, то вероятность попадания в этот интервал равна 1:
()1
в
а
fxdx
=
∫
. (65)
Т.к. constxf
=
)( , то
()1
в
а
fxdx
=
∫
или 1)( =
b
a
xxf , или 1))((
=
−
abxf . Откуда
a
b
xf
−
=
1
)( .
Функция распределения
1
()()
хх
xa
Fxfxdxdx
baba
−∞−∞
−
===
−−
∫∫
.
Таким образом функция распределения равномерного закона равна:
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
