Сапожников С.З. Китанин Э.Л. Техническая термодинамика и теплопередача

Подождите немного. Документ загружается.

Одна из распространенных формулировок первого начала

термодинамики такова: невозможно создать двигатель, который

мог бы бесконечно совершать работу без подвода энергии извне

(такую машину принято называть вечным двигателем первого

рода (perpetuum mobile (ppm-1))). Двигатель, который мог бы всю

теплоту, полученную рабочим телом от горячей среды,

преобразовать в работу, не отдавая сколько-нибудь теплоты

холодной среде, принято называть вечным двигателем второго

рода (ppm-2). Введение этих терминов позволяет свести воедино

формулировки первого и второго начал: невозможно создать

вечный двигатель ни первого, ни второго рода.

Кроме приведенных формулировок, в разделе 1.5.5 мы

рассмотрим и другие, а теперь обратимся к циклу, занимающему

особое место в термодинамике, — к циклу Карно.

1.5.4. Цикл Карно. Теорема Карно

В 1824г. С. Карно предложил цикл, который состоит из двух

изотермических и двух адиабатных процессов (рис. 30). Этот цикл

имеет огромное значение для оценки эффективности

преобразования энергии в реальных (и сколь угодно сложных)

циклах тепловых двигателей и холодильных машин. В знак

признания заслуг С. Карно и значения его работ для современной

термодинамики предложенный им цикл назван циклом Карно.

Рассмотрим цикл Карно подробнее. Для осуществления

процесса Т = const нужна среда с постоянной температурой, которая

не менялась бы при отводе или подводе теплоты (такая среда

должна иметь бесконечно большую теплоемкость). В цикле Карно

действуют горячая изотермическая среда с температурой T

холодная изотермическая среда с температурой Т

(от англ. hot —

горячий, cold — холодный).

Рис. 30.

Рабочее тело получает теплоту от горячей среды и

изотермически расширяется (процесс 1–2). Затем тепловой контакт

с горячей средой нарушается, и рабочее тело совершает адиабатное

расширение 2–3, которое заканчивается, когда температура

рабочего тела приближается к Т

. При соприкосновении с холодной

средой рабочее тело совершает изотермическое сжатие 3–4, после

чего вновь “отрывается” от изотермы и совершает адиабатное

сжатие 4–1, возвращаясь в начальное состояние 1. Если

температура рабочего тела в процессе 1–2 с точностью до

бесконечно малой величины dT

равна температуре горячей среды

(Т

= T

– dT

), а в процессе 3–4 температура Т

= Т

+ dT

, причем

все процессы являются равновесными, то цикл Карно обратим. На

участке 1–2 подводится теплота q

, на участке 3–4 отводится

теплота q

(на рис. 30 показано стрелками).

Если провести рассматриваемый цикл в обратном

направлении, то от холодной среды будет отведено столько же

теплоты, сколько подведено было в прямом цикле, а к горячей

среде подведено столько же, сколько было отведено от нее в

прямом цикле (с точностью до бесконечно малых). Работа,

необходимая для проведения обратного цикла с той же точностью,

равна работе, получаемой в прямом цикле, т. е. дополнительных

затрат энергии на возврат рабочего тела в исходную точку не

потребуется.

Если перепады температур ∆Т

= T

–T

, ∆Т

= T

– Т

имеют

конечное значение, либо часть процессов неравновесна, то цикл

Карно становится необратимым, и работа, необходимая на

проведение обратного цикла, больше работы, полученной в прямом

цикле.

Вычислим КПД обратимого цикла Карно, в котором рабочим

телом является идеальный газ. Для этого удобно использовать

формулу (1.50). Вычислим q

и q

;ln;ln

RTq

RTq ==

подставим эти значения в формулу (1.75); получим

)(ln

)(ln)(ln

121

433121

vvT

vvTvvT

−

=η

(1.76)

Рассмотрим теперь адиабатные процессы 2–3, 3–4, используя

связь между объемом и температурой:

.)(и)(

1441

2332

−−

vvTTvvTT

(1.77)

Поскольку T

= Т

, а T

= T

, в выражениях (1.77) левые части

равны, следовательно равны и правые их части:

.;)()(

1243

vvvvvvvv

−−

Это позволяет определить термический КПД цикла Карно:

−

=η

Поскольку цикл обратим (Т

= T

– dT

; Т

= Т

+ dT

) то с

точностью до бесконечно малых

−

=η

(1.78)

Формула (1.78) выведена для рабочего тела, являющегося

идеальным газом. С. Карно доказал теорему, которая утверждает,

что КПД цикла Карно не зависит от рода рабочего тела (т. е.

формула (1.78) справедлива для любых рабочих тел).

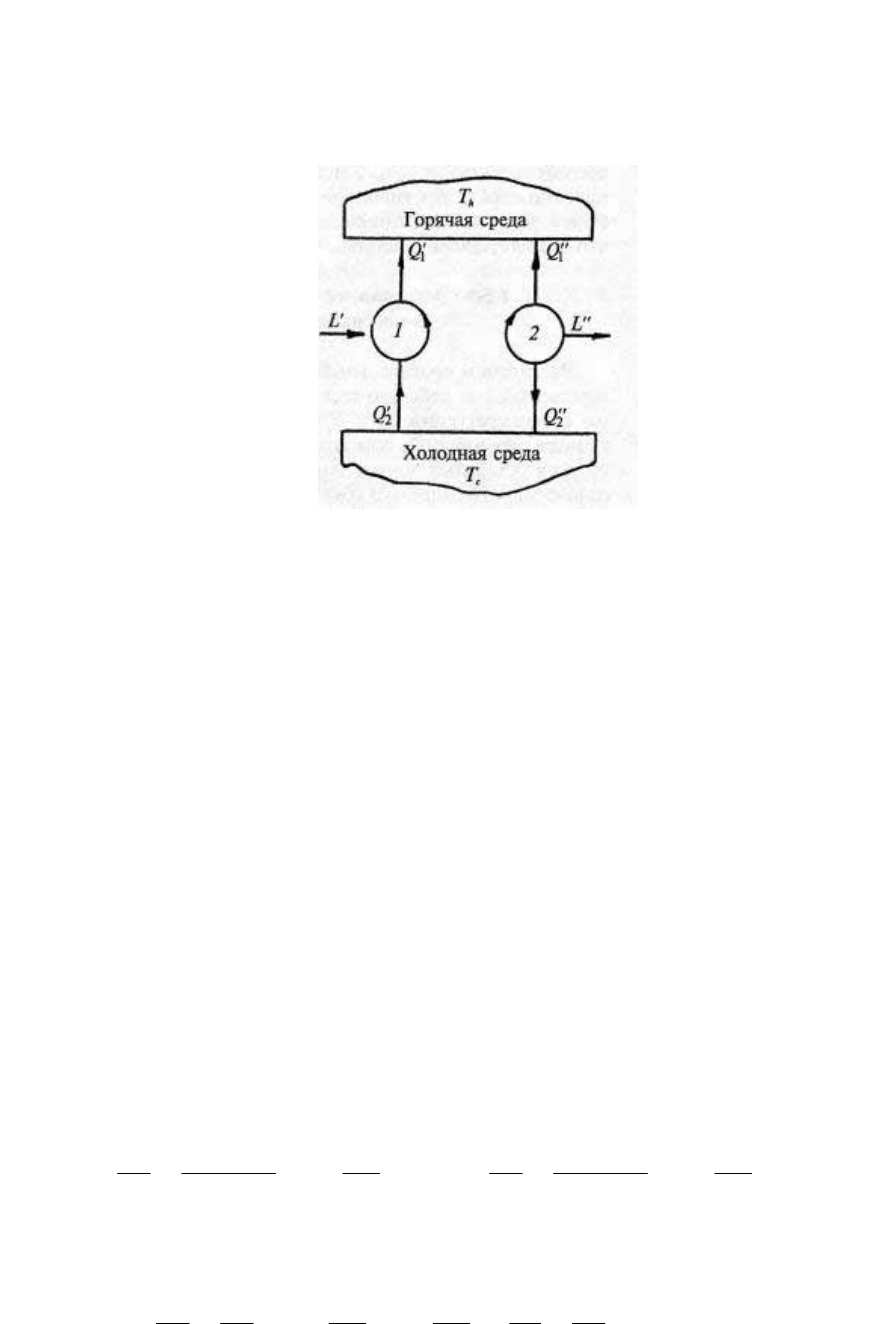
Доказать теорему Карно можно так. Пусть две тепловые

машины работают по обратимому циклу Карно при одних и тех же

температурах T

и Т

, причем рабочие тела в этих машинах

различны (рис. 31).

Рис. 31.

Допустим, что и КПД обоих циклов различны, например, η

. Процессы в циклах обратимы, поэтому, если первую машину

заставить работать по обратному циклу, то теплота и работа

изменят лишь знак, а не величину.

Допустим, что машина 1 работает по обратному циклу; его

параметры Q' и L'. Машина 2 работает по прямому циклу, его

параметры Q" и L". Количество рабочего тела в циклах не влияет на

КПД. Воспользуемся этим и подберем количество рабочего тела в

цикле 1 таким образом, чтобы теплота, отдаваемая им горячей

среде, равнялась теплоте, которая отводится от той же горячей

среды в цикле 2:

′

(1.79)

Поскольку

,1;1

′′

−=

′′

′

−

′

′′

′

=η

′

−=

′

−

′

=η

условие η

> η

принимает вид

.1;11;

′

−>

′′

′

−

′

′′

Отсюда следует, что L" > L', т. е. машина 2 совершает работу

большую, чем требуется на привод машины 1, в результате чего

образуется разность работ ∆L = L" – L'>0.

Одновременно необходимо признать, что Q

' > Q

", т. е.

машина 1 забирает от холодной среды больше теплоты, чем

машина 2 той же среде отдает. Образуется избыток теплоты ∆Q =

' – Q

" >0. Итак, мы получили работу ∆L, используя теплоту

одной только горячей среды ∆Q, что противоречит второму началу

в формулировке М. Планка. Следовательно, допущение, что η

неверно. Аналогично доказывается невозможность

противоположного неравенства η

< η

, пoэтому единственно

приемлемым остается условие η

= η

, что и требовалось доказать.

1.5.5. Энтропия, ее изменение в обратимых и необратимых

процессах

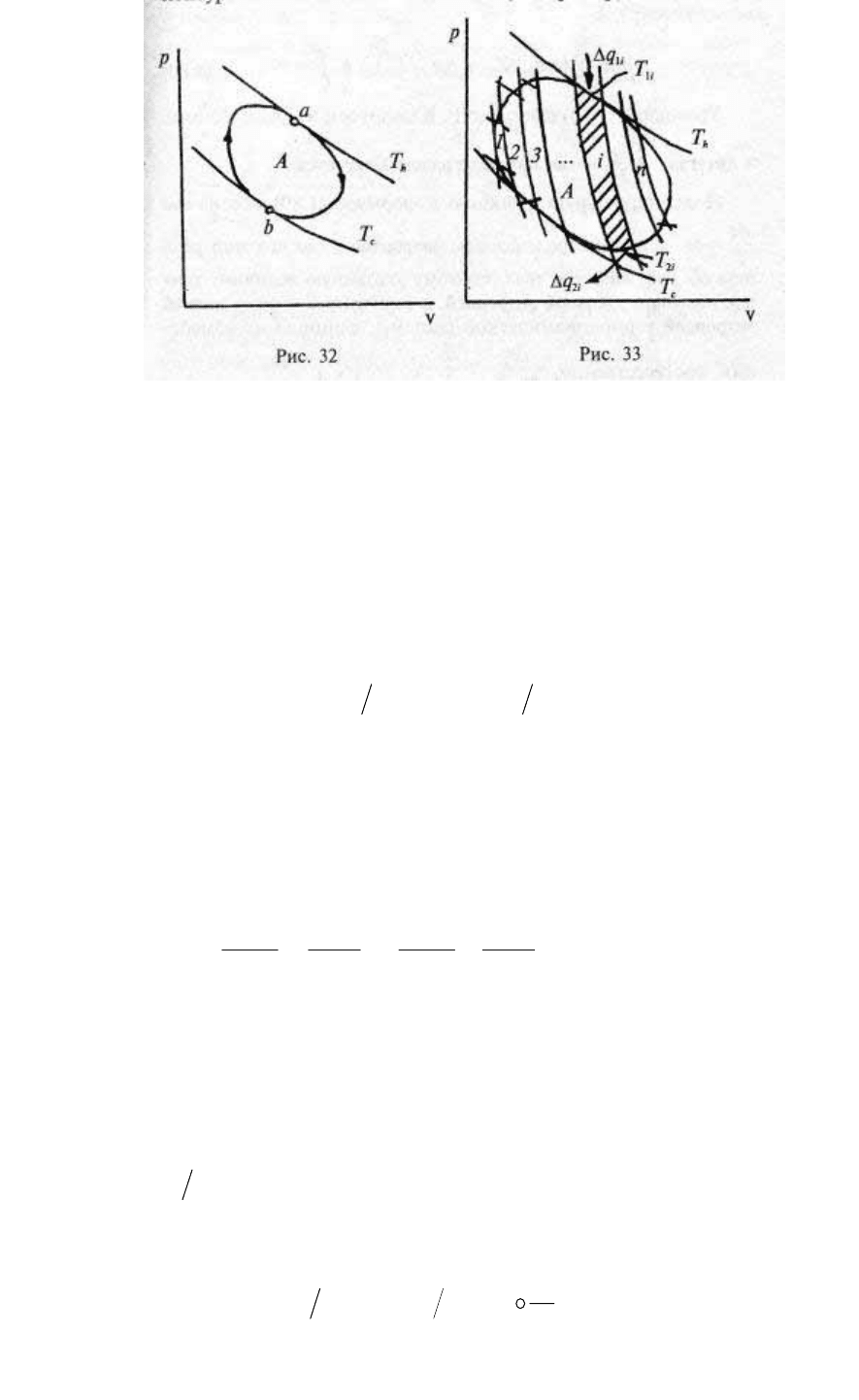
Рассмотрим произвольный круговой процесс А (рис. 32),

совершаемый 1 кг рабочего тела между горячей и холодной

средами с температурами T

и Т

соответственно. В точках а и b

температура рабочего тела совпадает с температурой этих сред, во

всех остальных точках цикла А температура рабочего тела

отличается от температур сред на конечную величину. Если даже

процессы расширения и сжатия пройдут бесконечно медленно, то

процесс теплообмена рабочего тела с горячей и холодной средами

будет необратим всюду, кроме точек а и b. Следовательно, будет

необратим и весь цикл А. Значит, для того, чтобы произвольный

цикл А стал обратимым, двух изотермических сред недостаточно.

Сколько же таких сред нужно?

Для ответа на этот вопрос проведем через цикл А ряд адиабат

(рис. 33), а через точки их пересечения с контуром цикла проведем

изотермы. Получившаяся фигура вписана внутрь контура А и

состоит из нескольких, например, из n циклов Карно.

Рис. 32. Рис. 33.

Для реализации элементарного обратимого цикла Карно

необходимы две изотермические среды с разной температурой, а

для того, чтобы обратимо провести приближенную модель

исходного цикла А, необходимо 2n изотермических сред (n горячих

и n холодных), причем их температуры должны находиться в

интервале от T

до Т

. Для каждого i-го цикла Карно

,11

1212 iiiiti

TTqq

−

∆

∆−=η

где

, ∆∆ — отведенная и подведенная в i-м цикле теплота; Т

и T

— температуры горячей и холодной сред, соответственно, в i-

м цикле.

Если учесть, что 0

∆

q , то

.0;

∆

−

В адиабатных процессах теплота не передается, поэтому

совокупность n циклов Карно близка по эффективности к

исходному циклу А (имеет тот же термический КПД). Суммируя

величины Tq

∆ отдельно по участкам подвода и отвода теплоты,

перейдем к пределу и вычислим интеграл по всему контуру А:

()

.0lim

1122

==∆+∆

∫

∑

∞→

iiii

TqTq

(1.80)

Уравнение (1.80) выведено Р. Клаузиусом и носит его имя, а

интеграл

∫

называют интегралом Клаузиуса.

Подынтегральную функцию в формуле (1.80) обозначим

∫

, а ее интеграл назовем энтропией s (до сих пор речь шла

об 1 кг рабочего тела, поэтому указанную величину точнее

называть удельной энтропией, а величину S = ms — полной

энтропией термодинамической системы; единицы их измерения,

соответственно,

кг

Дж

Ккг

Дж

⋅

Из формулы (1.80) следует, что интеграл Клаузиуса для

произвольного обратимого цикла равен нулю. Дифференциал

энтропии ds — полный дифференциал, поскольку сама энтропия

определяется только состоянием термодинамической системы. Для

энтропии справедливы и остальные требования к функциям

состояния; их, кроме полученного соотношения (1.80), выражают

равенства:

ddd

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

(1.81)

∑

(1.82)

Значения s считают известными с точностью до постоянной,

поскольку в расчеты входит разность ∆s = s

– s

Все изложенное роднит энтропию с такими функциями

состояния, как внутренняя энергия и энтальпия, но физический

смысл энтропии гораздо сложнее и глубже.

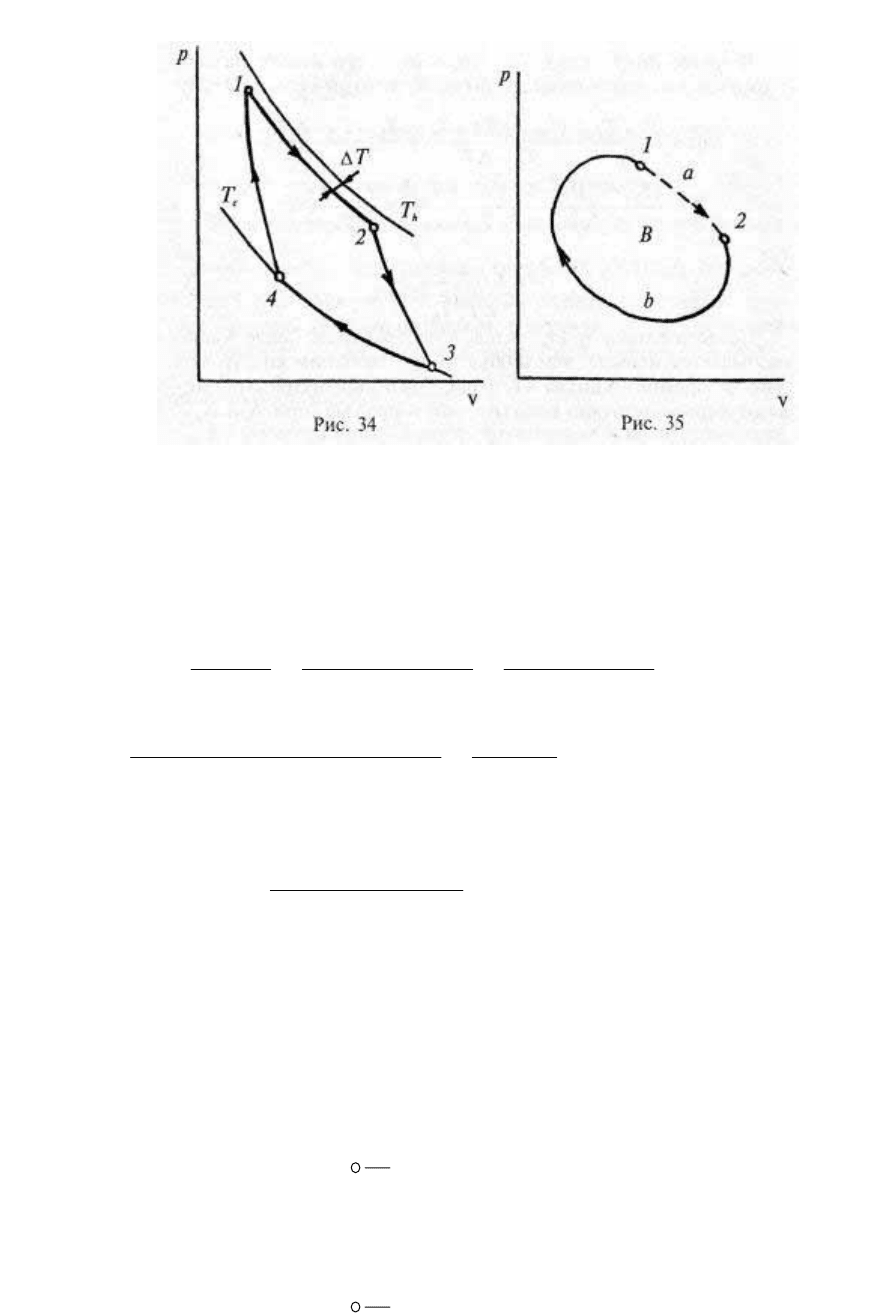
Исследуем понятие энтропии, используя представление о

КПД необратимого цикла. Начнем с цикла Карно, в котором на

участке подвода теплоты сохраняется конечная разность

температур ∆T (рис. 34).

Рис. 34 Рис. 35

В таком цикле КПД (строго говоря, его нельзя назвать

термическим, ведь в цикл входит необратимый процесс 1–2!):

[]

)/(1

где

)/1(

)/(1)(

)(

∆−

−∆−

−

∆−

−∆−−

∆−

∆

−

∆−

−

∆

−

=η

∗

chch

chc

TTT

TTTTT

TTT

Следовательно,

η<η

∗

: КПД в необратимом цикле Карно

оказывается меньше, чем в обратимом. Заполним контур любого

необратимого цикла А (см. рис. 33) n элементарными циклами

Карно; нетрудно показать, что в пределе, при n → ∞,

∫

(1.83)

Объединив формулы (1.83) и (1.80), получим

≤

∫

(1.84)

Другими словами — интеграл Клаузиуса не превышает

нуля ни для обратимых, ни для необратимых циклов любой

конфигурации.

Заметим, что определенную таким образом функцию s

можно использовать для описания любых процессов, а не только

термодинамических циклов.

Понятие дифференциала энтропии ds как величины, эк-

вивалентной подынтегральной функции интеграла Клаузиуса,

введено пока только для обратимого процесса. Рассмотрим теперь,

как меняется энтропия в процессе необратимом (рис. 35).

Допустим, что на отрезке 1а2 цикла В протекает необратимый

процесс (строго говоря, необратимые, а следовательно,

неравновесные процессы изображать в равновесной диаграмме

состояний нельзя, поэтому участок 1а2 показан на рис. 35

штриховой линией). К циклу В применимо соотношение (1.84).

Разобьем интеграл по замкнутому контуру В на два криволинейных

интеграла

<+=

∫∫∫

Второе слагаемое в левой части неравенства — интеграл по

равновесной части цикла, поэтому подынтегральное выражение

можно заменить на ds:

1212

sss

−==

∫∫

отсюда следует, что

()

,;0

122121

∫∫

>−=∆<−+

−

sssss

т. е. изменение энтропии в необратимом процессе больше,

чем интеграл Клаузиуса в этом же процессе.

Для элементарного необратимого процесса

d > . Если

вспомнить, что в обратимом процессе

d = , то можно записать

единую формулу

s ≥

(1.85)

справедливую как для обратимых, так и для необратимых

процессов. Знак равенства относится к обратимым процессам, а

знак неравенства — к необратимым.

Для теплоизолированных (адиабатных) систем, где q = 0,

равенство (1.85) принимает форму

≥

, причем и в этом случае

знак равенства относится к обратимым, а неравенства — к

необратимым процессам. Следовательно, при протекании любых

процессов энтропия теплоизолированной системы убывать не

может: она остается постоянной, если процессы обратимы, или

возрастает, если они необратимы.

Этот вывод является по существу еще одной формулировкой

второго начала: энтропия — мера необратимости процессов в

изолированной системе.

В изучении физического смысла энтропии выдающаяся роль

принадлежит Л. Больцману, который связал энтропию

термодинамической системы в некотором состоянии с термо-

динамической вероятностью этого состояния.

Термодинамическая вероятность коренным образом

отличается от вероятности математической. Поясним это на

примере. Пусть 1 кг газа в некотором состоянии имеет температуру

700 К. Известно, что температура — статистическая

характеристика, пропорциональная среднеквадратичной скорости

молекул газа. Среднюю температуру 700 К можно поддерживать,

когда половина частиц газа имеет скорость, соответствующую

температуре 800 К, а половина — скорость, соответствующую

600 К (первое макросостояние), или же одна треть частиц имеет

скорость, соответствующую 600 К, одна треть — 700 К и одна

треть — 800 К (второе макросостояние) и т. д. Ясно, что таких

макросостояний множество, поэтому термодинамическая

вероятность состояния выражается большим целым числом

(тогда как математическая вероятность всегда меньше или равна 1);

она определяет число микросостояний, реализующих

макросостояние термодинамической системы.