Сапожников С.З. Китанин Э.Л. Техническая термодинамика и теплопередача

Подождите немного. Документ загружается.

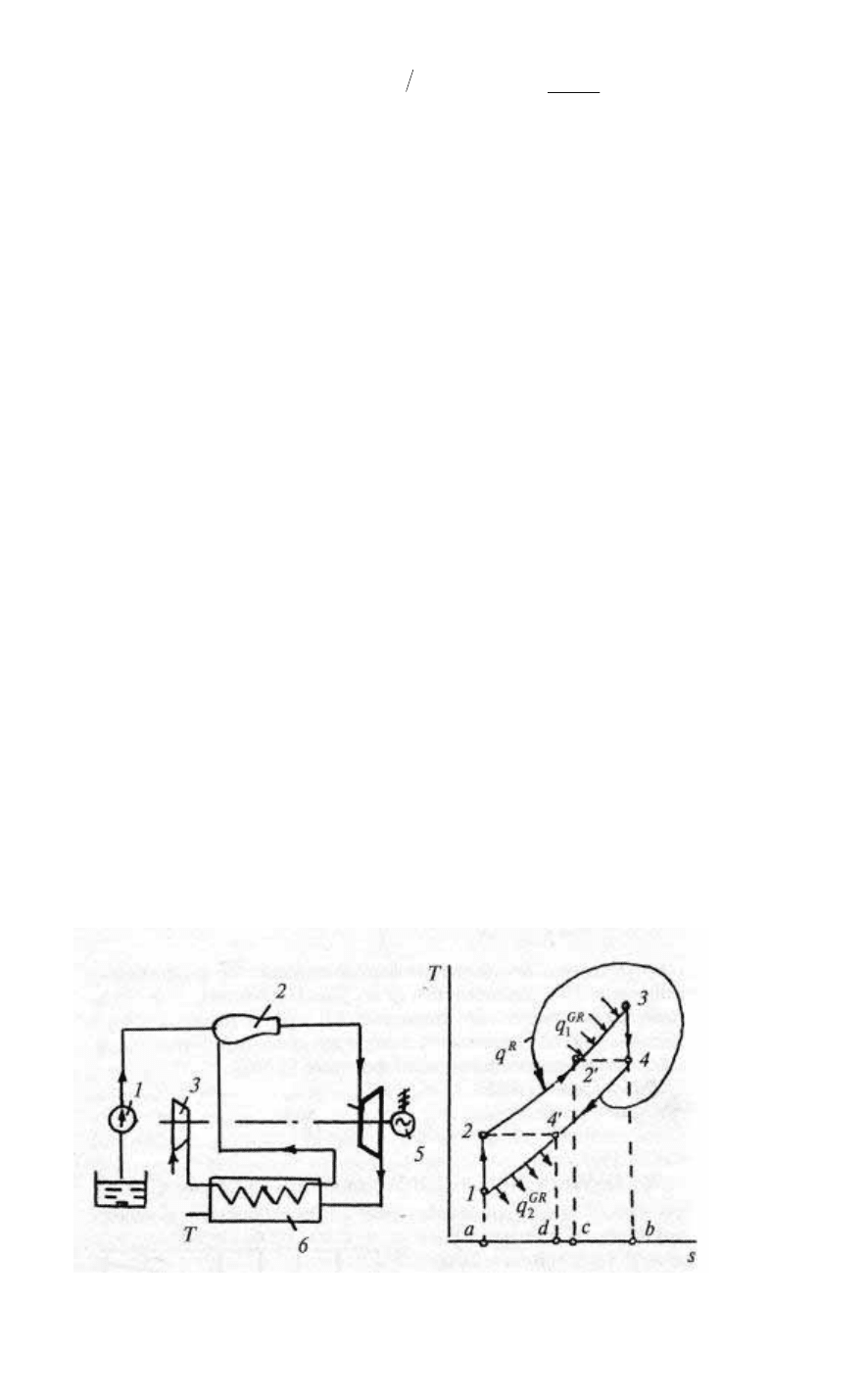
Работа цикла ГТУ

()

⎟

⎠

⎞

⎜

⎝

⎛

−−ρβ=η=

−

Tcql

(1.103

Из формул (1.102) и (1.103) видно, что значения

lиη тем

выше, чем больше значение k. Это приводит к мысли использовать

в качестве рабочего тела одноатомные гелий или аргон. Такой цикл

обязательно будет замкнутым, поэтому давление р

= р

можно

поднять значительно выше атмосферного; это сделает ГТУ гораздо

компактнее, что для транспортных систем немаловажно. Однако

замена рабочего тела потребует установить теплообменники как

для подвода теплоты q

, так и для отвода теплоты q

что неизбежно

усложнит конструкцию ГТУ.

1.7.3. Регенеративный цикл ГТУ

На лопатках турбины ГТУ газ расширяется полнее, чем в

цилиндре поршневого ДВС, однако его температура на выходе из

турбины Т

все еще заметно превышает температуру Т

окружающей среды (см. рис. 53). Если поток продуктов сгорания

привести в соприкосновение (без смешения) с потоком воздуха,

сжатого в компрессоре, то эффективность ГТУ повысится; такой

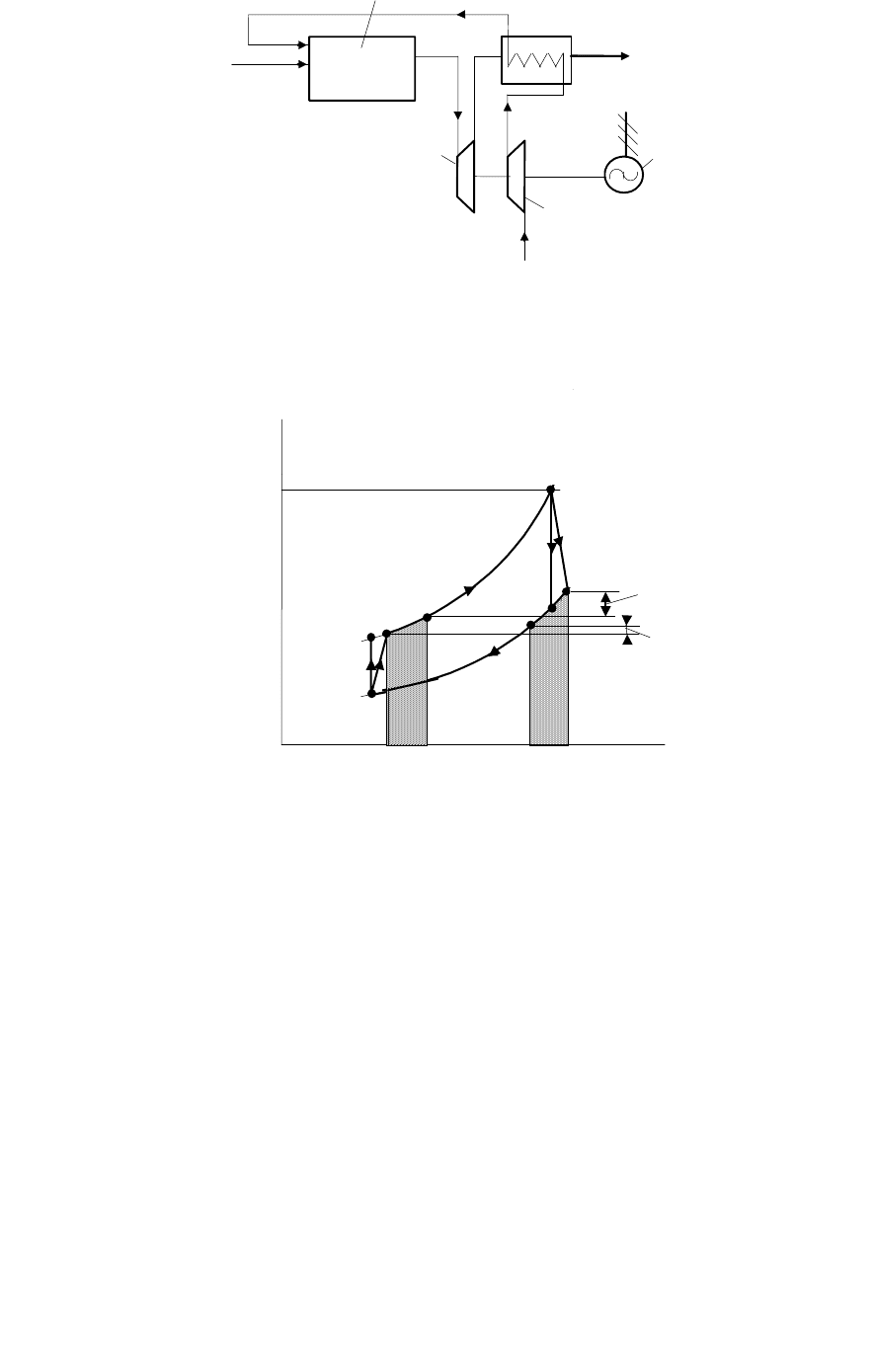
цикл ГТУ называют регенеративным. Схема ГТУ с регенерацией

теплоты (рис. 55) включает теплообменник

Рис. 55 Рис. 56

(регенератор) 6, в котором продукты сгорания отдают

теплоту

q сжатому воздуху (все прочие обозначения

соответствуют рис. 52).

Рассмотрим регенеративный цикл ГТУ, считая, что теплота

выхлопных газов полностью передается сжатому воздуху (рис. 56).

Без регенерации подведенная теплота

определялась бы

площадью под кривой 2–3 (пл. а23б), а отведенная q

— площадью

под кривой 2–3 (пл. а14б). В регенеративном цикле газ после

компрессора нагревается от температуры Т

до

′

= Т

. Выхлопные

газы из турбины, отдавая теплоту сжатому воздуху, охлаждаются,

но при этом, в соответствии со вторым началом, их температура не

может опуститься ниже

′

= Т

. В регенеративном цикле для

камера сгорания

топливо

воздух

компрессор

турбина

эл.генератор

выхлоп

2д

4д

-Т

-T

2д

подогрева газа до температуры Т

потребуется подвести теплоту

, эквивалентную пл. с2'Зб, которая, конечно, меньше, чем

теплота

q в цикле без регенерации. Меньше теплоты отдается и в

окружающую среду: эта величина

эквивалентна пл. а14'd и

ниже, чем q

Термический КПД регенеративного цикла ГТУ

(

)

()

.111

TTc

′

−

′

−=

′

−

′

−=−=η

(1.104)

В случае полной регенерации теплоты

′

= Т

′

= Т

Подставим в уравнение (1.104) значения температур Т

и Т

вычисленные по формулам, указанным в разд. 1.7.2; получим

(

)

()

−

⋅=

−

−=η

Но в адиабатных процессах 1–2 и 3–4

−

β=

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

а в изобарных процессах 2–3 и 4–1 р

=р

, p

, поэтому Т

/Т

, и

max

−

βγ

−=

⋅

−=−=−=η

(1.105)

где 1

14max

>=γ TT — степень подогрева воздуха за счет

регенерации (индекс “mах” означает, что теплота продуктов

сгорания используется полностью).

Сравнение формул (1.105) и (1.102) показывает, что

регенерация повышает термический КПД ГТУ:

η>η

что вполне объяснимо: при регенерации среднеинтегральная

температура подвода теплоты повышается, среднеинтегральная

температура отвода понижается, поэтому эквивалентный цикл

Карно совершается в большем интервале температур.

При анализе мы предполагали, что теплота выхлопных газов

полностью возвращается в цикл, а сжатый воздух может быть

нагрет до температуры газов, выходящих из турбины. В

действительности нагреть воздух до максимальной температуры

выхлопных газов не удается. Это несколько снижает прирост

термического КПД; тем не менее, регенерация теплоты в цикле

Брайтона заметно повышает эффективность ГТУ.

1.7.4. Эффективность реальных циклов

Эффективность реальных циклов поршневых ДВС и ГТУ

существенно меньше, чем определенная через их термические КПД,

поскольку циклы состоят из реальных, а значит, необратимых

процессов.

Причиной необратимости может быть рассеяние энергии за

счет трения при течении рабочего тела в межлопаточных каналах

ГТУ, в коллекторах, клапанах и цилиндрах ДВС, в подшипниках,

трансмиссии и т. д. В КПД таких циклов правильнее вводить не

физическую работу l, а действительную

(от англ. rеаl —

действительная). Вычисленный таким образом КПД называют

внутренним КПД цикла

η (от англ. intеrnal):

=η

Однако если, например, 4,0

, то невозможно сказать,

“хороший” это цикл или “плохой”: неясно ведь, в какой мере

связана величина

η с необратимыми потерями в цикле, а в

какой — с уровнем температур горячей и холодной сред.

Представим величину

, по-другому:

toit

ηη=η==η

(1.106)

Здесь

=η — внутренний относительный КПД, он

характеризует влияние необратимости процессов на эффективность

преобразования теплоты в работу и численно равен отношению

действительной работы цикла к теоретически возможной.

Поскольку в любом цикле, согласно первому началу,

,dd

lpvvpl =−==

∫

(1.107)

значение

η можно определить как через физическую работу l, так

и через работу техническую l

. Выбор определяется только

удобством расчетов: для циклов ГТУ удобнее использовать l

, а для

циклов ДВС — l.

Ясно, что в цикле ГТУ (см. рис. 53) действительная

техническая работа

2-т14-т3т

rrr

lll −=

(1.108)

где

2-т14-т3

, — действительная техническая работа турбины и

компрессора, соответственно.

Поскольку 0,0

2-т14-т3

ll , равенство (1.108) следовало бы

представить в форме

;

2-т14-т3т

rrr

lll −=

знак модуля далее опускаем исключительно в силу традиции.

Величины

2-т14-т3

и свяжем с технической работой обратимых

процессов расширения и сжатия

2-т14-т3

и ll

(

)

;

43430

4-т3

4304-т3

hhll

−η=⋅η=

−−

(1.109)

210

2-т1

−−

−

(1.110)

где

210430

−

ηη

— относительные внутренние КПД турбины и

компрессора, соответственно.

Значения

210430

−

ηη

определяют теоретически или

экспериментально; оба способа сложны и выходят за пределы

нашего курса. Далее полагаем, что эти величины заранее заданы.

Поскольку в любом случае 1,1

210430

−

из формул

(1.109) и (1.110) следует, что

2-т1

4-т3

llll

необратимость

уменьшает техническую работу расширения и увеличивает

техническую работу сжатия.

Вычислим теперь

η , для всего цикла ГТУ, используя

равенства (1.108)-(1.110):

()

()()

()

()()

1243

210

43430

1243

210

43430

TTTT

hhhh

−−−

−

−−η

−−−

−

−−η

=η

−

(1.111)

Для современных турбин и компрессоров

90,0...86,0,92,0...88,0

210430

η=η

−− ii

. Положим

9,0

210430

≈η=η

−− ii

и рассчитаем значение

η . Для цикла со

степенью повышения давления β = 8. По формуле (1.102) найдем,

что 448,0

=η

, а расчет по формуле (1.111) даст 665,0

=η

поэтому .298,0665,0448,0 =⋅=η

Однако значение

η не учитывает потерь энергии на трение в

подшипниках, элементах трансмиссии и т. д. Если каждый из n

элементов ГТУ имеет КПД

то эффективный КПД установки

∏∏

ηη=ηηη=η

(1.112)

(символ

∏

j 1

означает произведение всех

от j = 1 до j =n).

Полученному выше значению

η и реальным

соответствует 27,0=η

т. е. только 27 % теплоты сгорания

топлива преобразуется в полезную работу ГТУ.

Аналогично рассчитывают значение

для циклов ДВС. Так,

например, для ДВС, работающего по циклу Отто (см. рис. 44),

()

()()

()

()()

1243

210

43430

1243

210

43430

TTTT

eeee

−−−

−

−−η

−−−

−

−−η

=η

−

(1.113)

где

210430

−

ηη

— относительные внутренние КПД процессов

расширения и сжатия рабочего тела в цилиндре, соответственно.

Методика расчета не меняется. Для ДВС со степенью сжатия ε

= 8 при

85,0

210430

≈η≈η

−− ii

получаем 62,0

=η

, 565,0=η

откуда 35,0=η

. Эффективный КПД будет еще ниже:

.31,0...28,0=η

Эффективный КПД цикла Дизеля определяют по сходной,

хотя и более громоздкой формуле; при ε = 14 получаем

.34,0...30,0≈η

Необратимость меняет ход процессов расширения и сжатия на

диаграммах состояний (как уже отмечалось, необратимые процессы

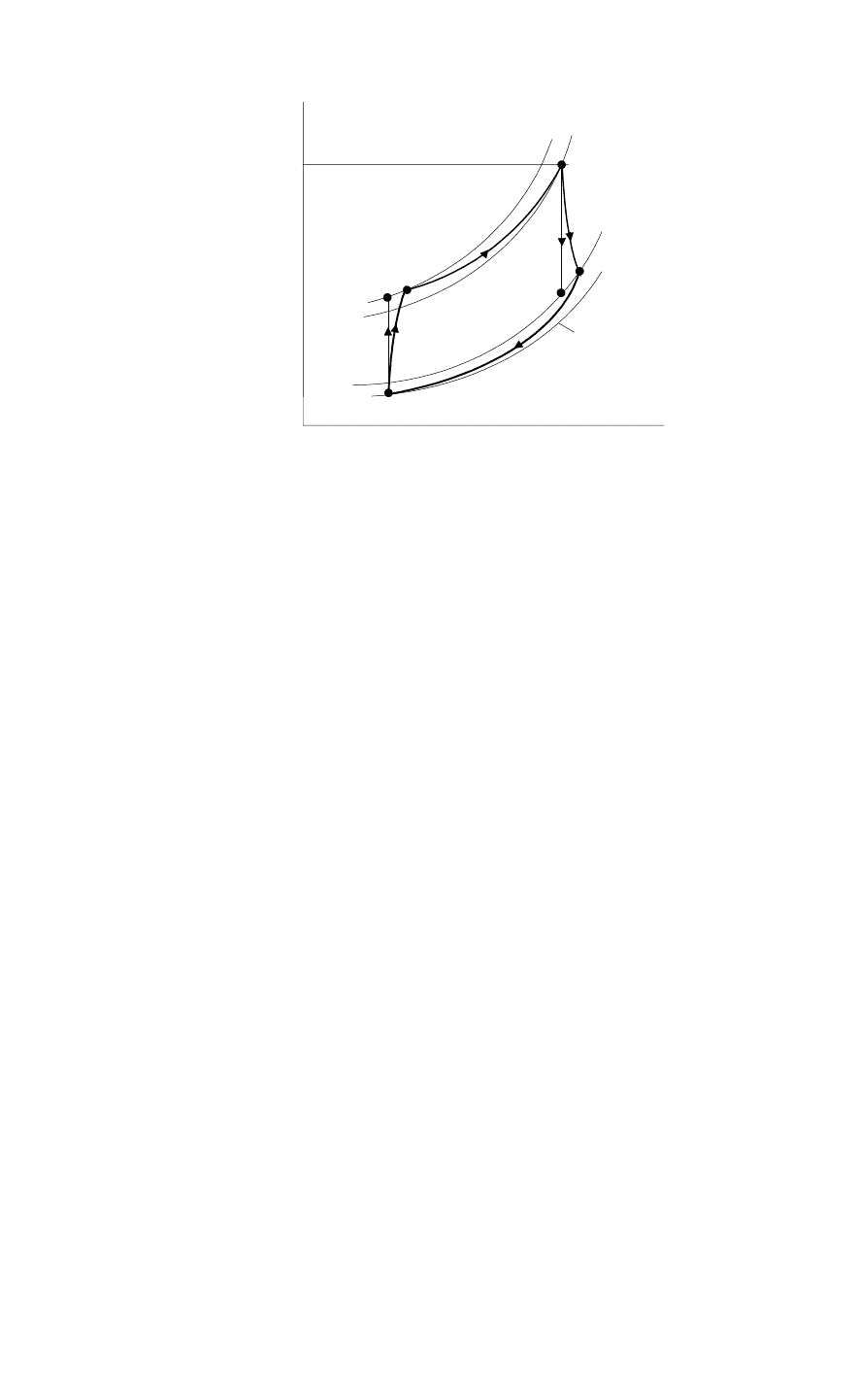
можно изображать на этих диаграммах только условно). На рис. 57

показаны циклы ГТУ: обратимый 12341 и необратимый (реальный)

1. В реальном цикле кривые расширения и сжатия

отклоняются от изоэнтропийных вертикалей: в соответствии со

вторым началом, энтропия в необратимых адиабатных процессах 1–

и 3–4

возрастает. Площади криволинейных трапеций пл. a13

b и

пл. c34

d эквивалентны потерям теплоты на трение. Поскольку

процессы1–2

и 3–4

адиабатны, теплота трения в окружающую

среду не отводится, а целиком возвращается в поток рабочего тела.

Аналогично “деформируются” необратимые циклы ДВС: адиабаты

расширения и сжатия отклоняются от линий s = const.

Рис. 57.

Полученные выше зависимости носят универсальный

характер и могут быть, в частности, использованы для оценки

эффективности циклов паросиловых установок (см. разд. 1.9). При

этом, правда, в формулах вида (1.111) и (1.113) должны стоять

только значения энтальпии и внутренней энергии: замена

TceTch

∆=∆∆=∆ , справедлива лишь для совершенного газа.

1.8. ТЕРМОДИНАМИКА РЕАЛЬНЫХ РАБОЧИХ ТЕЛ

1.8.1. Уравнение состояния реальных газов

При относительно невысоких давлениях и не слишком низких

температурах уравнение Клапейрона-Менделеева удовлетвори-

тельно описывает состояние большинства газов. Однако с

повышением давления или при снижении температуры расчет по

уравнению (1.5) дает существенные отклонения от действительных

термических параметров. Жидкое и парообразное состояние

вещества вообще не может быть описано уравнением этого типа.

В 1873 году голландский физик И. Ван-дер-Ваальс предложил

термическое уравнение состояния, в котором попытался учесть

отличия реальных газов от модели, заложенной в уравнение

Клапейрона-Менделеева:

()

RTbv

p =−

⎟

⎠

⎞

⎜

⎝

⎛

(1.114)

Здесь поправка b учитывает, что молекулы имеют

собственный объем, а сжатие или расширение газа может идти

только за счет изменения межмолекулярных расстояний. Величина

a/v

учитывает дальние взаимодействия молекул, т. е. некоторое

“внутреннее” давление в термодинамической системе.

Коэффициенты а и b для каждого вещества Ван-дер-Ваальс считал

постоянным.

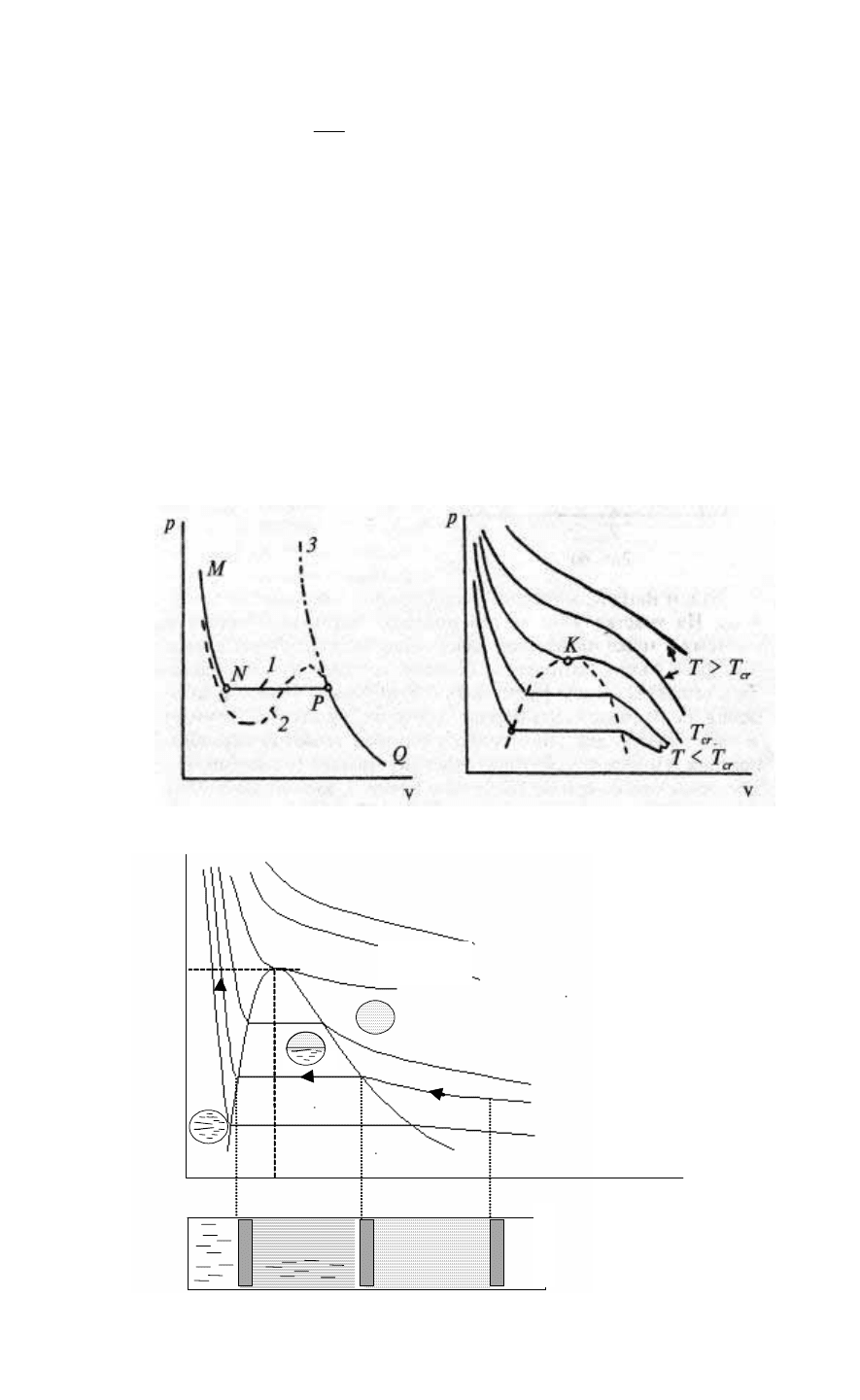
Рис. 58 Рис. 59

кр

t<t

кр

t=t

кр

t>t

кр

100

Сравним изотермы, рассчитанные по уравнениям (1.5) и

(1.114), с изотермами одного из реальных веществ, например, воды

(рис. 58). Изотерма идеального газа 3 совпадает с

экспериментальной кривой MNPQ только при больших значениях v

и малых р. Изотерма Ван-дер-Ваальса 2 дает лучшее совпадение, но

на среднем участке имеет “волну”, не подтверждаемую

экспериментом. Отметим, что отрезок MN реального

изотермического процесса 1 находится в области жидкого

состояния вещества, отрезок Р–Q — парообразного, а отрезок

NP — в области, где одновременно присутствуют как жидкость, так

и пар.

Уравнение Ван-дер-Ваальса для точных оценок непригодно,

но, в отличие от уравнения Клапейрона–Менделеева,

может описать поведение веществ, находящихся в жидком

или парообразном состоянии. Существуют и другие уравнения

состояния (Бертло, Дитеричи, Камерлинг–Оннеса, Боголюбова и

Майера, Вукаловича и Новикова), однако ни одно из них не

является “всеобщим”. Диаграммы состояний и расчетные таблицы

строят по экспериментальным данным и уравнениям состояния для

реальных веществ.

Для большинства реальных рабочих тел диаграмма состояний

р–v имеет вид, представленный на рис. 59. На ней выделяется точка

К, в которой изотерма имеет перегиб. Точку К впервые обнаружил

Д.И. Менделеев, сейчас ее называют критической точкой, а

Рис.9.3

кр

T>T

кр