Сапожников С.З. Китанин Э.Л. Техническая термодинамика и теплопередача

Подождите немного. Документ загружается.

поскольку она также является функцией процесса). Иначе обстоит

дело с внутренней энергией, которая является функцией состояния:

каким бы путем ни переходила термодинамическая система из

состояния 1 в состояние 2, изменение внутренней энергии будет

одним и тем же. Уравнения (1.22) и (1.23) примут вид

;

212121

∫

−−−

+∆=

leq

(1.26)

peq

(1.27)

В этой форме их используют для расчета процессов в любых

термодинамических системах.

1.3.2. Внутренняя энергия как функция состояния

Мы установили, что состояния однородной

термодинамической системы задают любые два термических

параметра, например, v и Т. Именно эту пару удобнее использовать

в качестве аргументов функции е = е (v, Т). Такое соотношение

называют калорическим уравнением состояния (от англ.

caloric — тепловой), а внутреннюю энергию е считают одной из

калорических функций состояния.

Подобно термическому уравнению состояния, для

калорического уравнения необходимы дополнительные сведения о

рабочем теле — экспериментальные или расчетные. Зависимость

внутренней энергии различных веществ от термических параметров

v и Т приведена в справочных таблицах.

Значение ∆е не зависит от вида процесса или, что то же, от

пути интегрирования. Такие функции называют аналитическими,

некоторые их свойства используем в дальнейших рассуждениях.

Применительно к внутренней энергии е эти свойства таковы.

1. Дифференциал функции состояния е является полным

дифференциалом:

.ddd T

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

(1.28)

(индекс около частных производных показывает, какой параметр

состояния остается неизменным).

2. Интеграл по замкнутому контуру от функции состояния е

равен нулю:

∫

= .0de

(1.29)

Физически это означает, что в круговом процессе (цикле), где

начальное и конечное состояния совпадают, e

= е

, de = 0.

3. Все функции состояния являются аддитивными: если

термодинамическая система состоит из n “подсистем” с

внутренними энергиями е

, то внутренняя энергия всей системы

∑

(1.30)

Внутреннюю энергию принято задавать с точностью до

постоянной. Сама эта постоянная для термодинамики значения не

имеет, поскольку в расчеты входит изменение энергии: разность

внутренних энергий термодинамической системы в двух точках

процесса.

Подставим значение de из уравнения (1.28) в

дифференциальную форму уравнения первого начала (1.27),

получим соотношение

,ddd vp

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

(1.27а)

которое является общим уравнением первого начала для любых

термодинамических систем, совершающих работу расширения.

1.3.3. Энтальпия и ее свойства

Внутренняя энергия — не единственная калорическая

функция состояния. Представим, что рабочее тело с удельным

объемом v надо ввести в среду с давлением р. Для этого

необходимо совершить работу pv, в чем легко убедиться,

рассматривая, например, тело в форме цилиндра объемом v = f∆

(f — площадь основания, ∆ — высота):

,)(

∆

pfl

где

l — работа “проталкивания” тела; pf — усилие

“проталкивания”; ∆ — перемещение тела.

Если сложить работу pv с внутренней энергией е, то получим

калорическую функцию состояния h = е + pv, которую называют

удельной энтальпией (очевидно, полной энтальпией следует

называть функцию Н= Е + рV). В дифференциальной форме

),d(

pveh

поэтому уравнение (1.27) примет вид

)d(

ppvhq

−

−=

(1.31)

Величины е, р и v однозначно определяют состояние

термодинамической системы, поэтому величина h, как и е, является

функцией состояния и, следовательно, аналитической функцией.

Ее удобно задавать в виде h = h(p, Т). Полный дифференциал

энтальпии

;ddd T

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

(1.32)

изменение энтальпии в цикле

∫

= ;0dh

(1.33)

энтальпия — аддитивная функция:

∑

(1.34)

значения энтальпии всегда известны с точностью до постоянной,

они сведены в таблицы, где заданы как функции давления и

температуры.

Уравнения первого начала (1.27а) теперь можно записать в

виде

.ddd pv

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

(1.27б)

Выбор той или иной формы первого начала диктуется только

удобством расчетов и в принципе совершенно произволен. Можно,

в частности, ввести в запись теплоемкость с

и с

. В изохорном

процессе (v = const, dv = 0)

поэтому на основании уравнения (1.27а)

;

⎟

⎠

⎞

⎜

⎝

⎛

аналогично в изобарном процессе (р = const, dp = 0) в соответствии

с уравнением (1.27б)

⎟

⎠

⎞

⎜

⎝

⎛

Отсюда

.ddd

;ddd

Tcq

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∂

(1.35)

В таком виде уравнения первого начала можно использовать

для исследования процессов с различными рабочими телами,

однако для этого необходимо знать производные (de/dv)

или

(dh/dp)

1.3.4. Уравнение первого начала для идеального газа

Значение частных производных

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

и наиболее

просто определить для идеального газа.

Гей-Люссак, а позже Джоуль поставили опыт, позволивший

ответить на вопрос, как зависит внутренняя энергия идеального газа

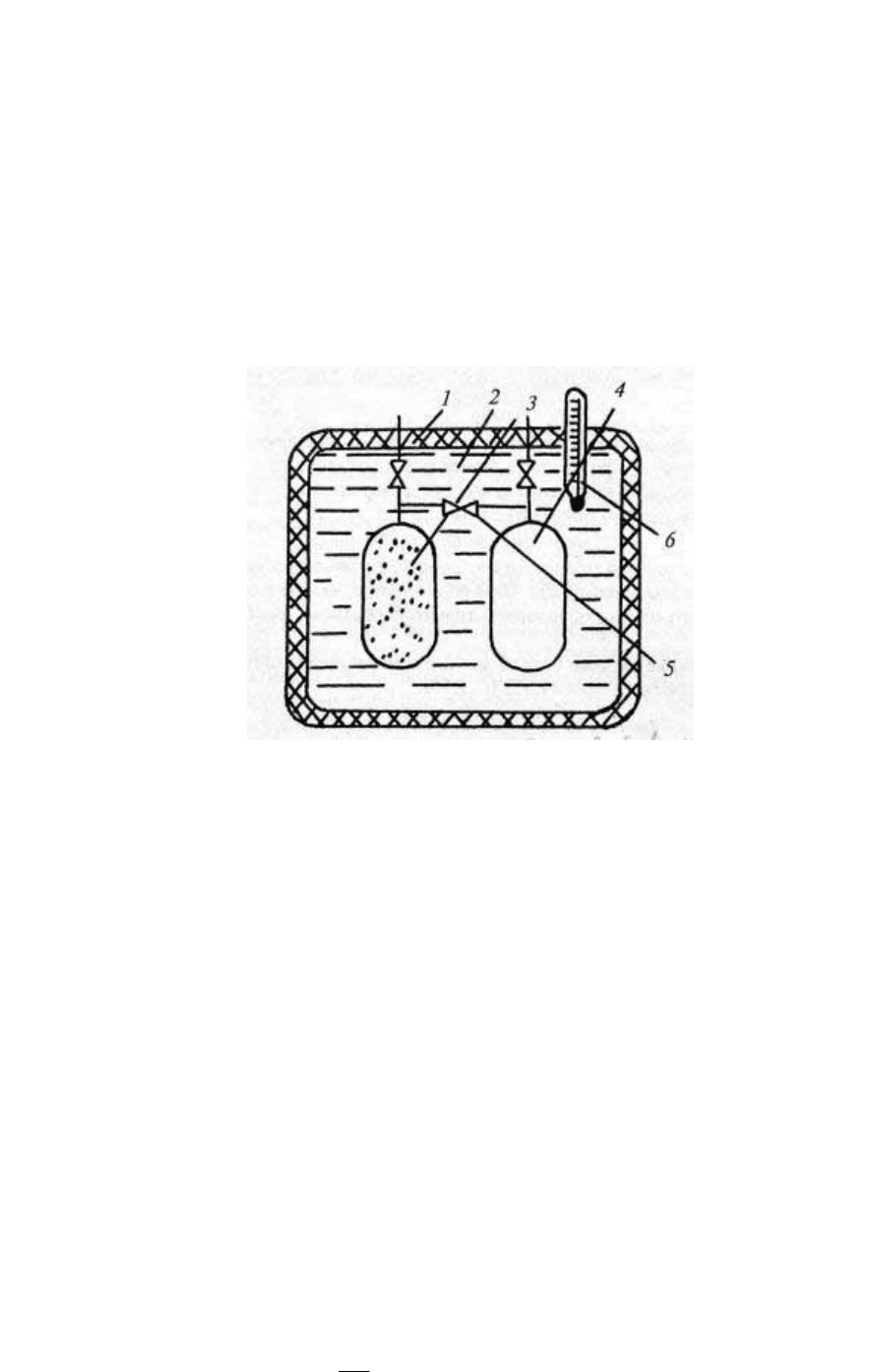
от объема, а энтальпия от давления. В термостат 1 (рис. 7),

наполненный водой 2, помещали два одинаковых сосуда 3 и 4,

разделенные закрытым вентилем 5. В сосуде 1 находился воздух

под давлением, близким к атмосферному (почти идеально-газовое

состояние), сосуд 4 был хорошо вакуумирован. После замера

температуры воды термометром 6 открывали вентиль 5, и газ

частично перетекал в сосуд 4, увеличивая свой объем вдвое, после

чего снова измеряли температуру. Если при расширении

температура несколько изменялась, то через некоторое время она

возвращалась к первоначальному значению.

Рис. 7.

Работа, совершаемая газом в процессе расширения, равна

нулю. Действительно, расширение носит неравновесный характер,

и значит, для расчета необходимо воспользоваться формулой (1.24),

в которую входит р

(внешнее давление). Внешним давлением в

данном случае является давление в вакуумированном сосуде, т. е. р

= 0. Теплоты воздух также не отдал и не получил (теплоизоляция

сосуда была почти идеальной), а поскольку температура воды в

сосуде не изменилась, то не изменилась и внутренняя энергия

воздуха: ∆е = 0.

Итак, при постоянной температуре объем воздуха возрос, а

внутренняя энергия не изменилась:

⎟

⎠

⎞

⎜

⎝

⎛

(1.36)

значит, внутренняя энергия идеального газа не зависит от

объема. Зная это, легко показать, что в опыте Гей-Люссака–Джоуля

соблюдается также условие

⎟

⎠

⎞

⎜

⎝

⎛

(1.37)

т. е. энтальпия идеального газа не зависит от давления.

Полученные результаты приводят к выводу, что полные

дифференциалы внутренней энергии и энтальпии для идеальных

газов равны соответственно

.ddиdd TchTce

(1.38)

Эти равенства представляют собой калорические уравнения

состояния идеального газа. Они равноценны, выбор для расчетов

любого из них обусловлен только удобством преобразований.

Уравнение первого начала для идеального газа запишем,

используя соотношения (1.35) и (1.38):

.ddd

;ddd

pvTcq

vpTcq

−=

(1.39)

(1.40)

Отсюда следует, что

)d(

=−

С другой стороны, по уравнению Клапейрона–Meнделеева

)d(

поэтому

.Rcc

−

(1.41)

Выражение (1.41) называют формулой Майера: из него

следует, что удельная изобарная теплоемкость газа больше его

удельной изохорной теплоемкости на величину газовой

постоянной.

Умножая обе части формулы (1.41) на молярную массу µ,

получаем уравнение

uvp

Rcc

−

µµ

(1.42)

из которого следует, что мольные теплоемкости

µp

µv

всех

идеальных газов отличаются на величину универсальной газовой

постоянной R

Пользуясь формулами (1.39)–(1.42), важно помнить, что они

справедливы только для идеального газа, а для других рабочих тел

либо соблюдаются приближенно, либо просто неприменимы.

1.4. АНАЛИЗ ПРОЦЕССОВ С ИДЕАЛЬНЫМ ГАЗОМ

В задачу такого анализа входят определение теплоты и

работы, изменения энтальпии и внутренней энергии в процессах

идеального газа при условии х = const, где х — один из термических

или калорических параметров состояния. Начнем с традиционных

процессов р = const, v = const и Т= const.

1.4.1. Изобарный процесс

Процессы, протекающие в камерах сгорания газотурбинных

двигателей и в теплообменниках, сгорание топлива в двигателях

Дизеля и т. д. сопровождаются расширением или сжатием газа (с

подводом или отводом теплоты) при постоянном давлении. Эти

процессы называют изобарными (р = const). Связь термических

параметров газа в любых двух точках 1 и 2 такого процесса

задается законом Гей-Люссака:

В рабочей диаграмме состояний изобарные процессы

изображают горизонтальными линиями (рис. 8). Теплота,

подведенная к идеальному газу в процессе р = const, расходуется на

изменение энтальпии. Действительно, из формулы (1.40) при dp = 0

Рис. 8.

следует, что

;dd Tch

если теплоемкость с

табулирована, то в изобарном процессе

передается теплота

.)(d

1221

122

tctcttcTcq

−=−=

∫

−

(1.43)

При малых изменениях температуры, а значит, и изобарой

теплоемкости с

, можно считать, что ).(

1221

TTcq

−

≅

−

Легко

рассчитать и работу изобарного процесса. Исходя из общего

определения работы расширения рабочего тела, получим

);(d

1221

vvpvpl

−==

∫

−

(1.44)

численно работа

21−p

l равна площади прямоугольника а12b (см.

рис. 8).

1.4.2. Изохорный процесс

Изохорные процессы обычно связаны с подводом теплоты к

газу, заключенному в жесткий (недеформируемый) замкнутый

объем. Происходят они также в камерах сгорания карбюраторных

двигателей, некоторых газотурбинных установок и т. д. В р–v-

диаграмме эти процессы изображаются семейством вертикальных

линий (рис. 9).

Рис. 9.

Термические параметры изохорного процесса 1–2

определяются законом Шарля:

Работа газа в изохорном процессе равна нулю, поскольку dv =

−

(1.45)

Теплоту процесса рассчитаем, положив в формуле (1.39) dv =

0; тогда

Tcq

.)(d

1221

122

tctcttcTcq

−=−=

∫

−

(1.46)

Из равенств (1.45) и (1.46) следует, что в изохорном процессе

вся подведенная к термодинамической системе теплота идет на

изменение внутренней энергии.

Если теплоемкость c

слабо зависит от температуры, то можно

считать, что

).(

1221

TTcq

−

≅

−

1.4.3. Изотермический процесс

В энергетических установках, рабочее тело которых по

свойствам близко к идеальному газу, изотермические процессы

практически отсутствуют. Однако даже приближенная их

реализация позволяет значительно повысить эффективность многих

энергомашин, поэтому расчет процессов Т = const представляет

интерес хотя бы как предельно достижимый.

Уравнение изотермического процесса Т = const определяется

законом Бойля–Мариотта

2211

vpvp

где индексы 1 и 2 относятся к двум точкам на кривой

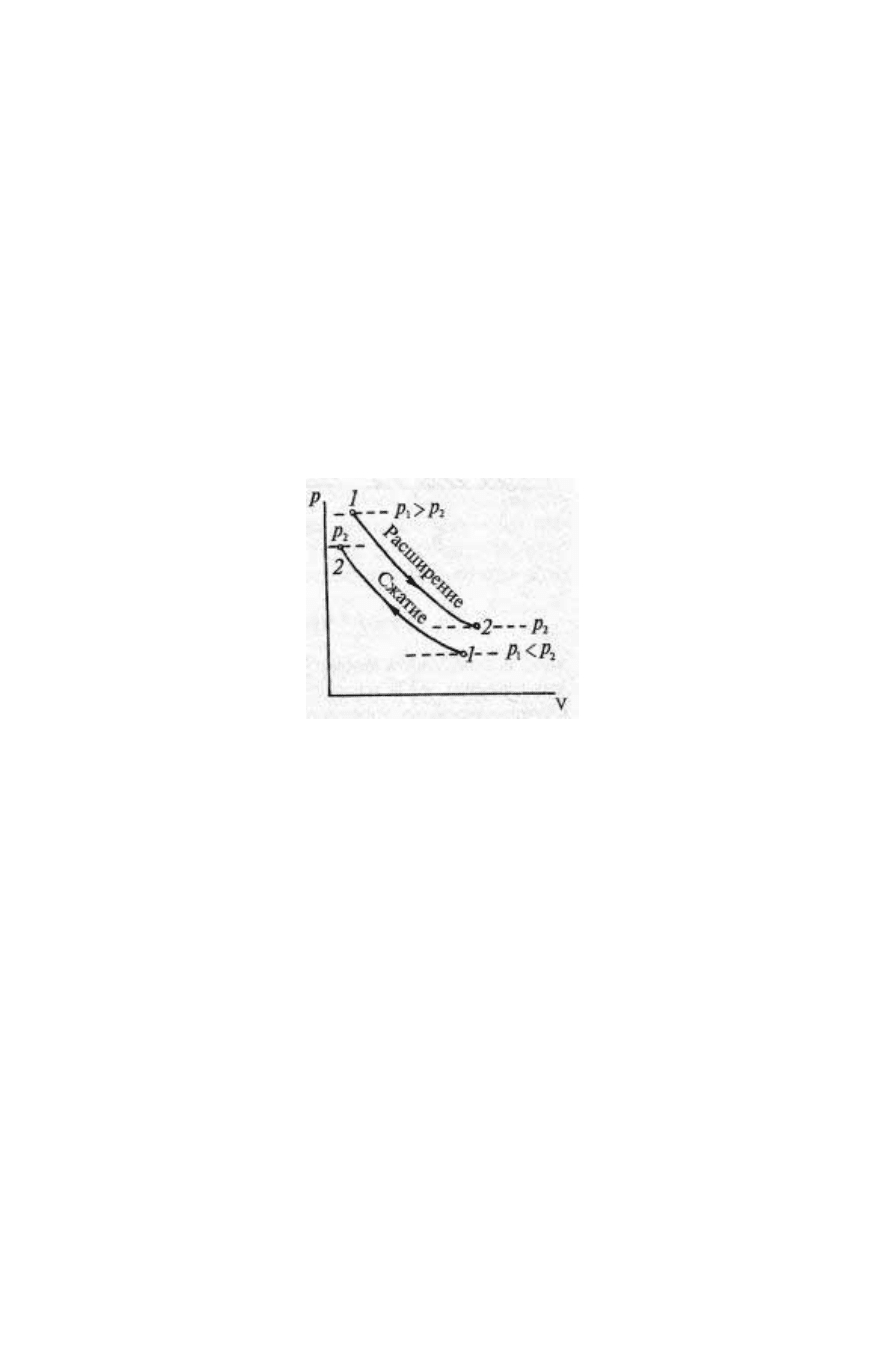
изотермического процесса. В рабочей диаграмме состояний

изотермы Т = const образуют семейство гипербол (рис. 10).

Рис. 10.

Ранее мы установили, что внутренняя энергия идеального газа

зависит только от температуры, а так как в рассматриваемом случае

Т = const, то е = const и de = 0. Из уравнения (1.27) следует, что при

этом

,dd lq

(1.47)

т. е. в изотермическом процессе идеального газа подведенная

теплота расходуется на совершение работы, и наоборот. В

интегральной форме уравнение (1.47) имеет вид

2121

−

(1.48)

Вычислим работу расширения идеального газа в

изотермическом процессе: