Сапожников С.З. Китанин Э.Л. Техническая термодинамика и теплопередача

Подождите немного. Документ загружается.

()

∫∫

−

.ln

1221

vpl

(1.49)

Выражение (1.49) можно записать по-другому, используя

уравнения Клапейрона–Менделеева и Бойля–Мариотта:

()

(

)

(

)

.lnlnln

122122121121

vvRTppvpvvvpl

−

(1.50)

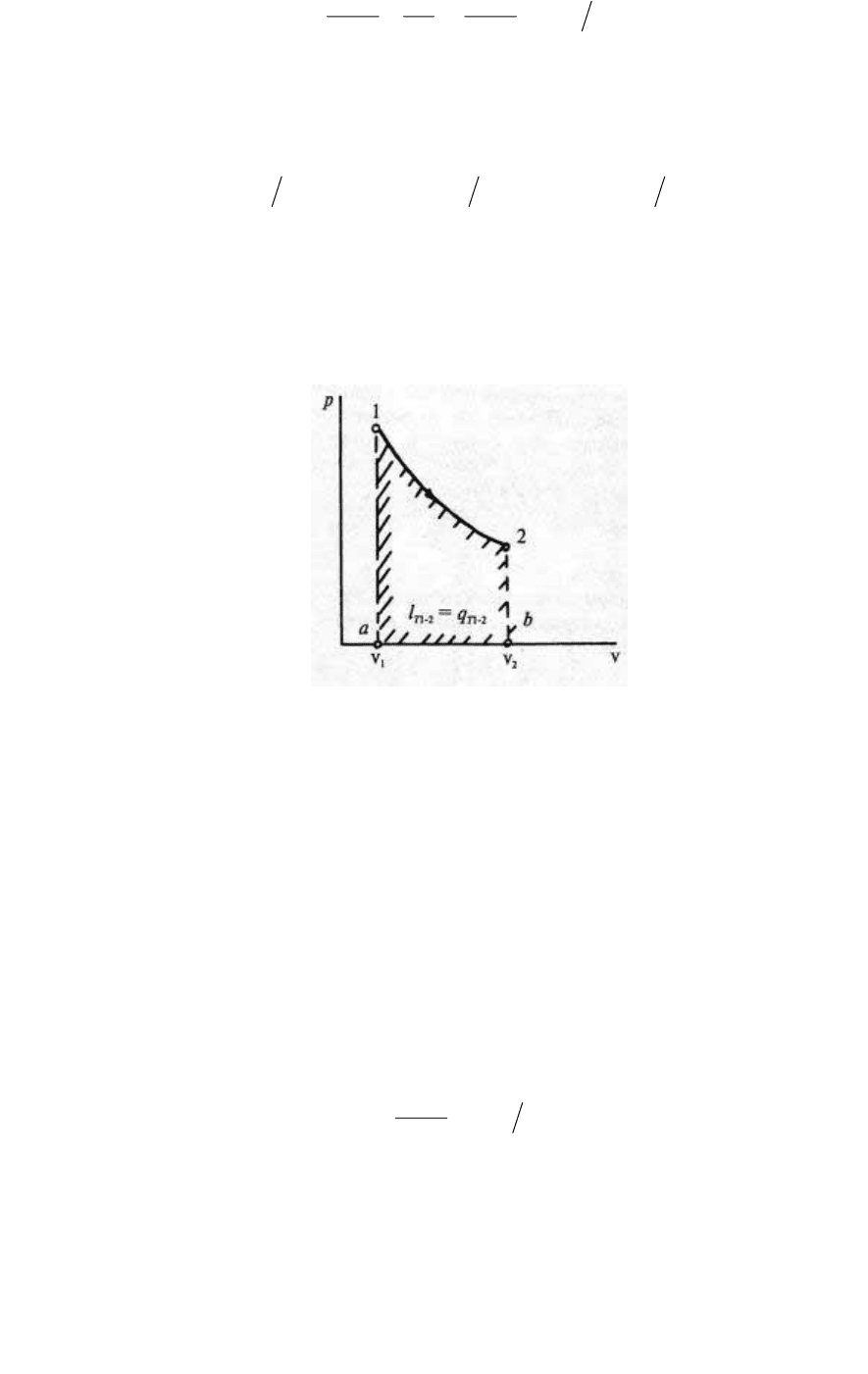
Работа, получаемая при изотермическом расширении от

начального объема v

, до конечного v

, в р–v-диаграмме

характеризуется площадью а12b (рис. 11).

Рис. 11.

В изотермическом процессе dT = 0, поэтому подвод любой

теплоты q

не меняет температуру системы. Формально это

означает, что теплоемкость в изотермическом процессе равна плюс-

минус бесконечности (с

= ±∞), поэтому расчет по формуле

)(

1221

TTcq

−=

−

связан с раскрытием неопределенности вида 0·∞.

Однако соотношение (1.48) позволяет рассчитать теплоту через

эквивалентную ей работу расширения:

()

;ln

122121

−−

либо использовать любую удобную форму записи (1.50). Ясно, что

площадь а12b на рис. 11 характеризует не только работу

изотермического процесса, но и его теплоту.

1.4.4. Адиабатный процесс

Адиабатным называют процесс, протекающий без подвода

или отвода теплоты. На практике “абсолютно адиабатных”

процессов не наблюдается, но процессы, достаточно близкие к

адиабатным, распространены чрезвычайно широко: газы,

обладающие свойствами идеальных, сжимаются в поршневых

двигателях и компрессорах, расширяются в турбинах почти

адиабатно.

При отсутствии теплоподвода и теплоотвода, т. е. при dq = 0 и

1–2

= 0, уравнение первого начала принимает вид

;

−

(1.51)

работа в адиабатном процессе совершается за счет изменения

внутренней энергии.

Рассмотрим связь между термическими параметрами в

адиабатном процессе. Для этого кроме уравнения (1.51) используем

уравнение первого начала (1.31), в котором положим dq = 0.

Получим dh = vdp.

Для идеального газа dh = c

dT, поэтому

.ddT pvc

(1.52)

Аналогично выглядят формулы, включающие внутреннюю

энергию е и теплоемкость c

.ddT,dd vpcvpe

−

−=

(1.53)

Из равенств (1.52) и (1.53) следует, что

const.

=−=

(1.54)

Для идеального газа величина

kcc

постоянна и носит

название коэффициента Пуассона, или показателя адиабаты.

Идеальный газ, у которого с

= const, c

= const, называют

совершенным, для него величина k зависит только от строения

молекул:

k= 1,66 для одноатомных газов;

k= 1,40 для двухатомных;

k = 1,33 для трех- и более атомных.

Для большинства технических газов в той области, где они

подчиняются уравнению Клапейрона–Менделеева, теплоемкости с

и c

заметно меняются с температурой, но величина

cck = от

температуры почти не зависит.

Последовательно преобразуя формулу (1.54), получим

const.

const;lnln;

;

+−=−=

−=⋅−=

∫∫

pvk

(1.55)

Уравнение (1.55) называют уравнением адиабаты Пуассона.

С помощью уравнения Клапейрона–Менделеева и уравнения

адиабаты Пуассона можно найти связь между любой парой

термических параметров. Подставим в уравнение (1.55)

значение

= и перенесем в правую часть все постоянные

величины; получим

const.

−k

(1.56)

Аналогично можно найти связь между р и Т:

const.

−

(1.57)

Построим кривую q = 0 в рабочей диаграмме состояний. Из

уравнения (1.55) следует, что р = const/v

, а поскольку k > 1, кривая

адиабатного процесса в р–v-диаграмме пройдет круче изотермы. На

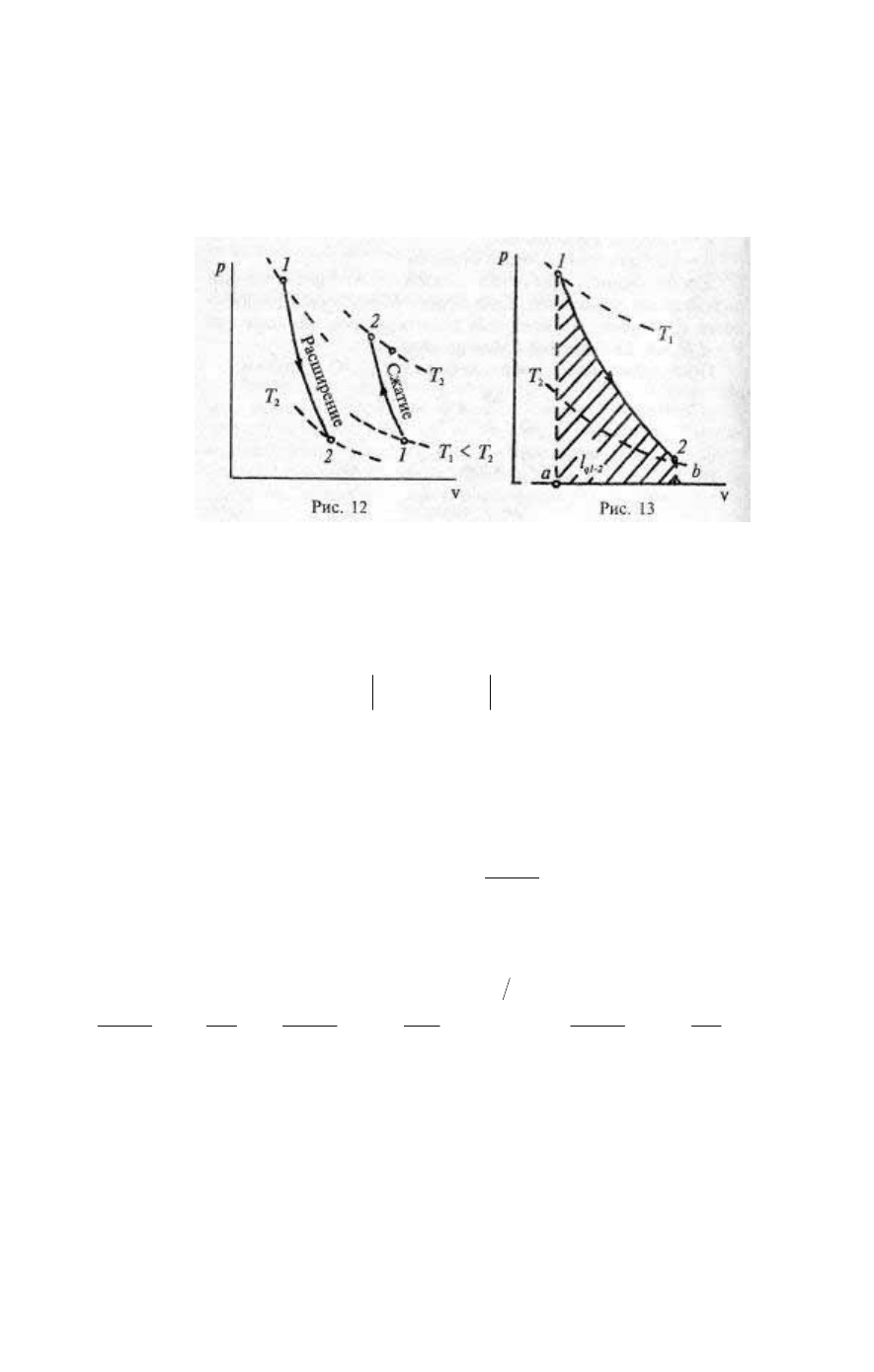
рис. 12 показаны две адиабаты: 1–2 и 3–4. В процессе 1–2 газ

расширяется, при этом его температура снижается; в процессе 3–4

газ сжимается и температура его повышается.

Теплота в адиабатном процессе равна нулю по самому

определению процесса. Таким образом, осталось найти лишь один

параметр взаимодействия газа с окружающей средой — работу.

Уравнения (1.27) и (1.38) показывают, что при dq = 0 dl =–

dT, откуда

∫

−=

−

Tcl

(1.58)

Рис. 12. Рис. 13

или, через среднюю теплоемкость,

tctcl

vmq

−=

−

(1.59)

Если газ совершенный (c

= const), то

).(

1221

TTcl

−

С учетом формулы Майера ,

−

поэтому

(

)

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

kkk

(1.60

)

Тот же результат можно получить, интегрируя выражение

(1.25) с подстановкой р = const/v

. Работа адиабатного процесса 1–2

численно равна площади а12b (рис. 13).

1.4.5. Политропные процессы

Политропные процессы — процессы идеального газа,

идущие при постоянной теплоемкости — названы по сочетанию

греческих слов гаоАл — много и трота — превращение. Все

рассмотренные ранее процессы — частные случаи политропных

(если, конечно, считать, что в них соблюдаются условия с

= const).

В политропных процессах, как и во всех остальных, соблюдается

первое начало термодинамики:

,ddd vpTcTc

где, с

— теплоемкость политропного процесса (политропная

теплоемкость).

Кроме того, при c

= const

const,

===

или в интегральной форме для процесса 1–2

const,1

const,

∆

−=

∆

−

(1.61)

(1.62)

т. е. в политропных процессах доля теплоты, переходящая в

работу, постоянна.

Получим уравнение политропы. Если в формулы (1.39) и

(1.40) подставить значение q = c

dT, то они примут вид

,ddd

pvTcTc

vpTcTc

−=

откуда следует, что

,d)d(

;d)d(

pvTcc

vpTcc

−=−

−

После почленного деления получим

)(

−=⋅

−

Величину

−

называют показателем политропы.

Дифференциальное уравнение политропы

−=

после интегрирования примет окончательную форму

const.=

(1.63)

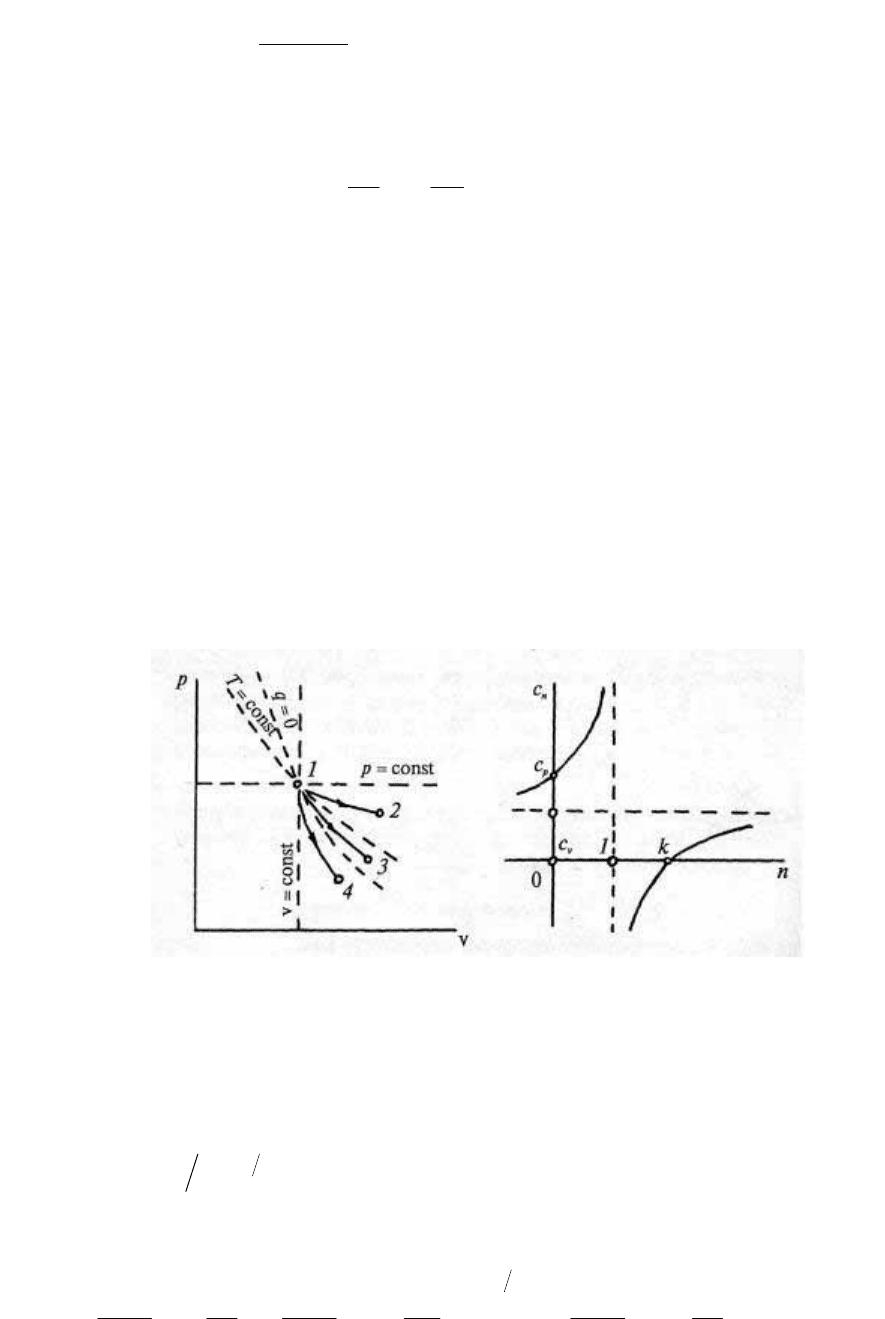
Политропные процессы могут не только совпадать с

рассмотренными процессами р = const, v = const, T= const, но и

проходить в р–v-диаграмме между ними (рис. 14). Процессу р =

const соответствует значение n = 0, v = const — n = ±∞, Т= const — n

= 1, a q = const — n = k, поэтому для процесса 1–2 0 < n < 1, для

процесса 1–3 1 < n < k, а для процесса 1–4 k<n<∞.

Рис. 14. Рис. 15.

Формально уравнение политропы (1.63) совпадает с

уравнением адиабаты Пуассона (1.55) при замене n на k, поэтому

его можно записать в виде

const,илиconst

−

TvpT

а работу политропного процесса определить как

(

)

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

nnn

(1.64

)

Теплоту, сообщаемую газу в политропном процессе, проще

всего определить по общей формуле

∫

−

Tcq

Если подставить в нее значение

−

, то получим

).(

1221

−

∫

−

(1.65)

Величина и знак с

зависят как от свойств газа (c

и k), так и от

характера процесса (т. е. от показателя политропы n). При n < 1 и n

> k с

> 0 (рис. 15). При n = 1 с

= ±∞ и функция с(n) терпит разрыв.

Мы уже обсуждали причины, по которым теплоемкость процесса Т

= const следует считать бесконечной. Если 1 < n < k, то с

< 0; это

означает, что при подводе теплоты температура газа понижается, и

наоборот.

Такое явление вполне объяснимо: ведь кроме подвода

теплоты существует еще одна форма взаимодействия —

совершение работы. Понижение температуры газа при подводе

теплоты означает, что одновременно газ совершает работу, причем

с работой энергии отводится больше, чем подводится с теплотой. В

результате внутренняя энергия газа уменьшается, что и приводит к

понижению температуры. Подобным образом объясняется и

повышение температуры при отводе теплоты: здесь прирост

энергии за счет совершения над газом работы сжатия превышает

потерю энергии за счет отвода теплоты.

Рис. 16. Рис. 17.

Для расчета произвольного политропного процесса по

уравнению (1.63) необходимо определить значение n. На кривой

процесса, полученной опытным путем, намечают две точки, в

которых известны термические параметры состояния (рис. 16).

Если считать процесс политропным, то из уравнения

const=

pv следует, что

vpvp

2211

= . Прологарифмируем это

равенство и получим показатель политропы:

.lnln

n =

(1.66)

Естественно, что рассчитать значение п ничуть не труднее,

если в точках 1 и 2 известны давление и температура или удельный

объем и температура газа.

Если зависимость р(v) носит сложный характер (рис. 17), то

весь процесс разбивают на участки, на каждом из которых можно

рассчитать свой показатель политропы. Эти показатели находят по

формулам, аналогичным равенству (1.66), для каждого участка 1–2,

2–3, 3–4. По найденным показателям n

, n

на отдельных

участках процесса рассчитывают теплоту и работу, а затем

суммируют их значения для всего процесса 1–2–3–4.

Описанный метод расчета (метод политроп) находит широкое

применение при анализе процессов в двигателях внутреннего

сгорания, компрессорах, газовых турбинах и т. д. В качестве

примера рассмотрим процесс сжатия газа, по свойствам близкого к

совершенному, в поршневом компрессоре.

1.4.6. Сжатие газа в поршневом компрессоре

Компрессором называют машину для сжатия газов и паров.

При сжатии газа в компрессоре обычно преследуют следующие

цели:

создать запас энергии для последующего совершения работы

(пневматические тормоза автомобилей, устройства для

передвижения под водой и т.д.);

повысить температуру газа для последующей отдачи теплоты

(холодильные установки);

обеспечить компактное хранение газа (газобаллонные

станции).

Типы и конструкции компрессоров разнообразны, но

термодинамические процессы в них достаточно сходны.

Рассмотрим работу поршневого компрессора (рис. 18), в

цилиндре 1 которого возвратно-поступательно движется поршень 2.

При движении поршня 2 вниз клапан 3 открывается, и газ

низкого давления поступает в цилиндр. После того, как поршень 2

дойдет до нижней мертвой точки, он начинает сжимать газ, причем

оба клапана 3 и 4 закрыты вплоть до момента, пока давление в

Рис. 18.

цилиндре 1 не достигнет заданного уровня. Затем открывается

клапан 4, и газ нагнетается в магистраль под действием

движущегося вверх поршня 2. В верхней мертвой точке нагнетание

заканчивается, клапан 4 закрывается, а клапан 3 открывается,

происходит новое всасывание и т. д.

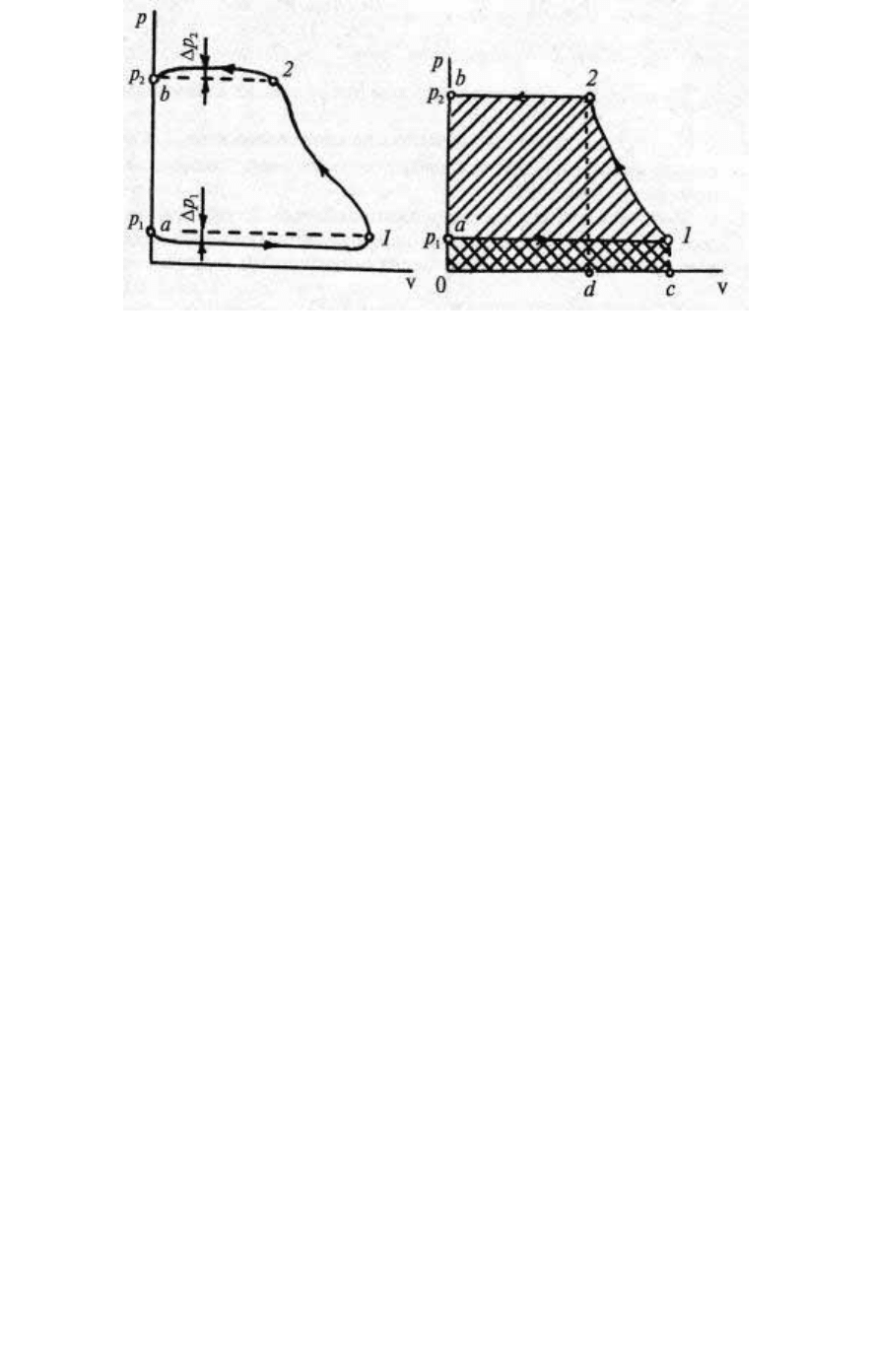
Рис. 19. Рис. 20.

Проследим за давлением газа в цилиндре в зависимости от

перемещения поршня (а значит, и от объема газа) и построим

диаграмму, которая носит название индикаторной. Если поршень

начинает движение от верхней мертвой точки, т. е. начальный

объем газа почти равен нулю, то индикаторная диаграмма примет

вид, представленный на рис. 19. Внешне она совпадает с обычной

р–v-диаграммой, но процессы всасывания а–1 и нагнетания 2–b

идут с переменной массой газа. Разрежение во впускном клапане

∆p

и избыточное давление перед выпускным ∆p

невелики по

сравнению с давлением внутри цилиндра; для термодинамического

анализа их вклад малозаметен. Рассмотрим идеализированный

процесс (рис. 20), происходящий при сжатии 1 кг газа от давления

до давления р

. Вначале рассчитаем работу процессов а–1, 1–2 и

2–b. Работа изобарного процесса а–1

;)0(d

1111

vpvpvpl

=−==

∫

−

(1.67)

аналогично выражается и работа процесса 2–b:

.)0(d

2222

vpvpvpl

−=−==

∫

−

(1.68)

Работа в процессе сжатия 1–2, характер которого пока

неизвестен,