Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking
Подождите немного. Документ загружается.


204
A.
SPERANZA
12
I I I
I I
10
-
-
-
8-
-
z-
6
-
-
a
v
4-
2-
0
4
-
I
&
01-
2
00-
5
-01-
-
-
-03
'
'
A
'
-01
00
01 02
03
OL
-01
00
01
02
03
04
-01
00
0.1
0.2
03
04
V
W
V
'
-0.2j
d
I
-031
'
!
'
'
-0.1
0.0
0.1
0.2
0.3
0.L
V
0.1
0.0
0.1
0.2
0.3
0.4
U
FIG.
2.
The
CDV
model
potential
V(U),
for
h,/H
=
0.05
as
a
function
of
the
zonal forcing
L'*.
(a)
If*
=
0.12:(b)
GI*
=
0.14:(c)
Lr*
=
0.18:(d)
U*
=
0.20;(e)
U*
=
0.24.
(FromBenzi
el
al.
1984a.)

PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
205
the potential barriers to be overcome in order to escape from the blocked and
zonal potential wells.
Barrier heights and exit times are shown in Table I. It is clear that dramatic
changes take place when the external forcing
U*
changes. The structural
dependence on
U*
can be stabilized if we include red noise of amplitude
E,
and decorrelation time
l/Au
in the zonal momentum equation. The effect
of the inclusion of red noise is in general to stabilize the unstable state. The
corresponding probability distribution can be proved to be
-
1
4
Am
R2
+
g2(
U)
(7
R2
+
g2(
U)
P(U)
=
where
R
=
2
Aoe/E,
and and
g
are functions of Udefined in Benzi
et
al.
(1
984).
In this case, the probability distributions take the form shown in Fig.
4.
It
can be seen that the inclusion of red noise reduces the occupation of the
zonal state, while leaving the probability of the blocked state relatively un-
changed. This behavior is due to the presence of a minimum of the function
g(
U)
at the resonant value of the zonal wind and to the fact that the reso-
nance value
is
located between the zonal and the blocked ones.
The general impression at this point is that we are dealing with a mecha-
nism of zonal-flow evolution which is basically unrealistic. The wave equa-
tion, on the other hand, seems to be, within the limits of a minimal theory,
TABLE
I.
BARRIER HEIGHTS
AND
EXIT TIMES
FOR
THE
CDV MODEL
AS
A
FUNCTION
OF
THE
ZONAL
FORCING
U*'
U*
V(1)
-
V(2)
V(2)
-
V(3) r(b1ock) r(zona1)
(N.D.)
(X (X
(days) (days)
0.10 2.17
0.004 76.6 180.1
0.12
1.76 0.6
1
18.1 43.6
0.14
I
.48
1.79 10.8 49.8
0.16 1.24
3.43 7.6 79.2
0.18
1.05
5.5
1
5.8
159.5
0.20
0.88
8.02 4.6 395.6
0.22
0.73 11.00
3.9
1.2~
103
0.24
0.6 1 14.30
3.4 4.3
x
103
0.26
0.49 18.10
3.0 1.8
X
lo4
0.28 0.40 22.20
2.8 9.6X
lo4
0.30 0.3
I
26.80 2.7
5.8
X
lo5
a
The nondimensional (N.D.) height of topography is
h,/
H
=
0.05.
The indices 1, 2, and 3 refer to blocked, zonal, and
intermediate states;
block)
and r(zona1) are times for the
blocking-to-zonal and zonal-to-blocking transitions, respec-
tively. (From Benzi
et
al.,
1984a.)
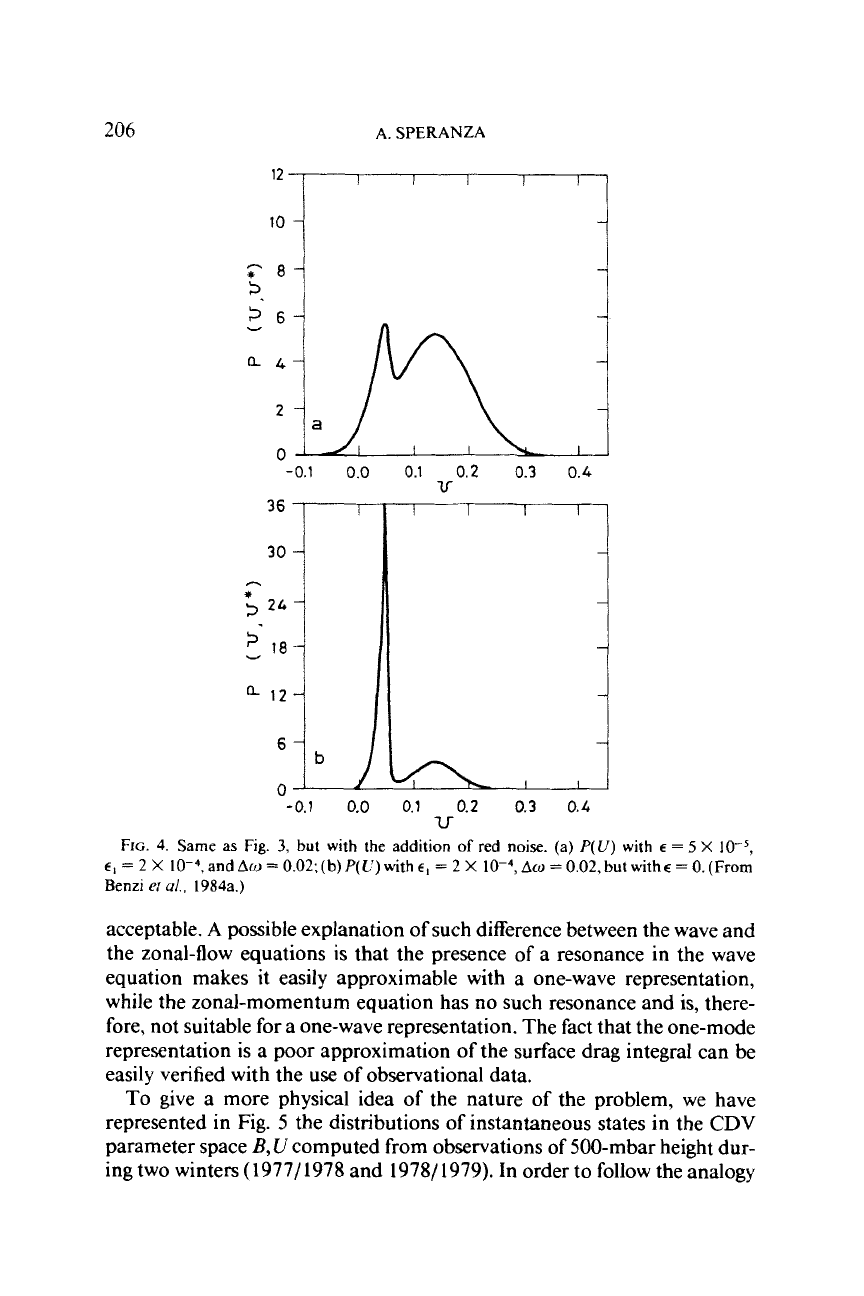
206
A.
SPERANZA
-0.1
0.0
0.1
0.2
0.3
0.4
U
36
0
-0.1
0.0
0.1
0.2
0.3
0.4
U
FIG.
4.
Same
as
Fig.
3,
but
with the addition
of
red
noise. (a)
P(U)
with
E
=
5
X
E,
=
2
X
10-4,andA~=0.02:(b)P(C')with~,
=2X
10-4,A~=0.02,butwith~=0.(From
Benzi
er
u/.,
1984a.)
acceptable. A possible explanation of such difference between the wave and
the zonal-flow equations
is
that the presence
of
a resonance in the wave
equation makes it easily approximable with a one-wave representation,
while the zonal-momentum equation has
no
such resonance and
is,
there-
fore, not suitable for a one-wave representation. The fact that the one-mode
representation is a poor approximation of the surface drag integral can be
easily verified with the
use
of observational data.
To
give a more physical idea of the nature of the problem, we have
represented in Fig.
5
the distributions of instantaneous states in the
CDV
parameter space
B,U
computed from observations
of
500-mbar height dur-
ing two winters
(1977/1978
and
1978/1979).
In order to follow the analogy

PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
207
FIG.
5.
Plot of the linear resonance of the CDV model and the form-drag law for different
values
of
U*. The circles represent the amplitude of wavenumber
3,
computed from observed
data of winters 1977/1978 and 1978/1979.
with the quasi-unidimensional model, the variables are integrated between
30”N
and
70”N.
The distribution
of
observed values
of
zonal wind ap-
pears much less dispersed than in
CDV.
No
similar disagreement with the
range
of
observed variability can be noticed in the wave amplitude.
It is clear that,
if
we accept the observed zonal-momentum distribution as
a phenomenological law and still insist on the idea
of
multiple equilibria, we
need a mechanism capable
of
equilibrating finite amplitude
of
the wave in a
limited range
of
zonal wind values.
This
is not possible in
CDV
because of the linear structure of the wave
equation, which does not allow the existence
of
different wave amplitudes
for the same zonal wind
U.
However, insertion
of
nonlinearity in the wave
equation can easily “bend” the resonance. The easiestZ way
of
producing
resonance bending consists of introducing weak nonlinearity into the solu-
More complex forms
of
nonlinearity can produce quite realistic “localized” stationary
flows,
as
shown by Malanotte Rizzoli and Malguzzi
(
1984)
and Pierrehumbert and Malguzzi
(I
984). The theory we
discuss
here is, however, essentially ‘‘global.’’
208
A.
SPERANZA
tions of the stationary, inviscid equation (the MS model: Malguzzi and
Speranza, 198
1
).
It
is
not difficult to prove that in the quasi-unidimensional limit, assuming
a cubic functional
q(v/),
we
obtain an equation
of
the
form
dxN
+
PY
+
(fo/H)h
=
-(P/WV
-
by3
(10)
Assuming, however, topography and nonlinearity to
be
both small and ofthe
same order, we can stabilize at finite amplitude the zero-order (linear, free
wave) solution of Eq.
(10):
(1
1)
v/(O)
=
A
exp(i
WUX)
+
(*)
-
UY
obtaining for the slowly varying
(X
=
EX),
slightly detuned (with respect to
resonant wavenumber
AK
=
Km
-
WU)
amplitude
A(X
Y)
=
YdY)
exPo
AKX)
+
(*)
(12)
a cubic equation
0
10
20
30
40
50
U
(mlsec)
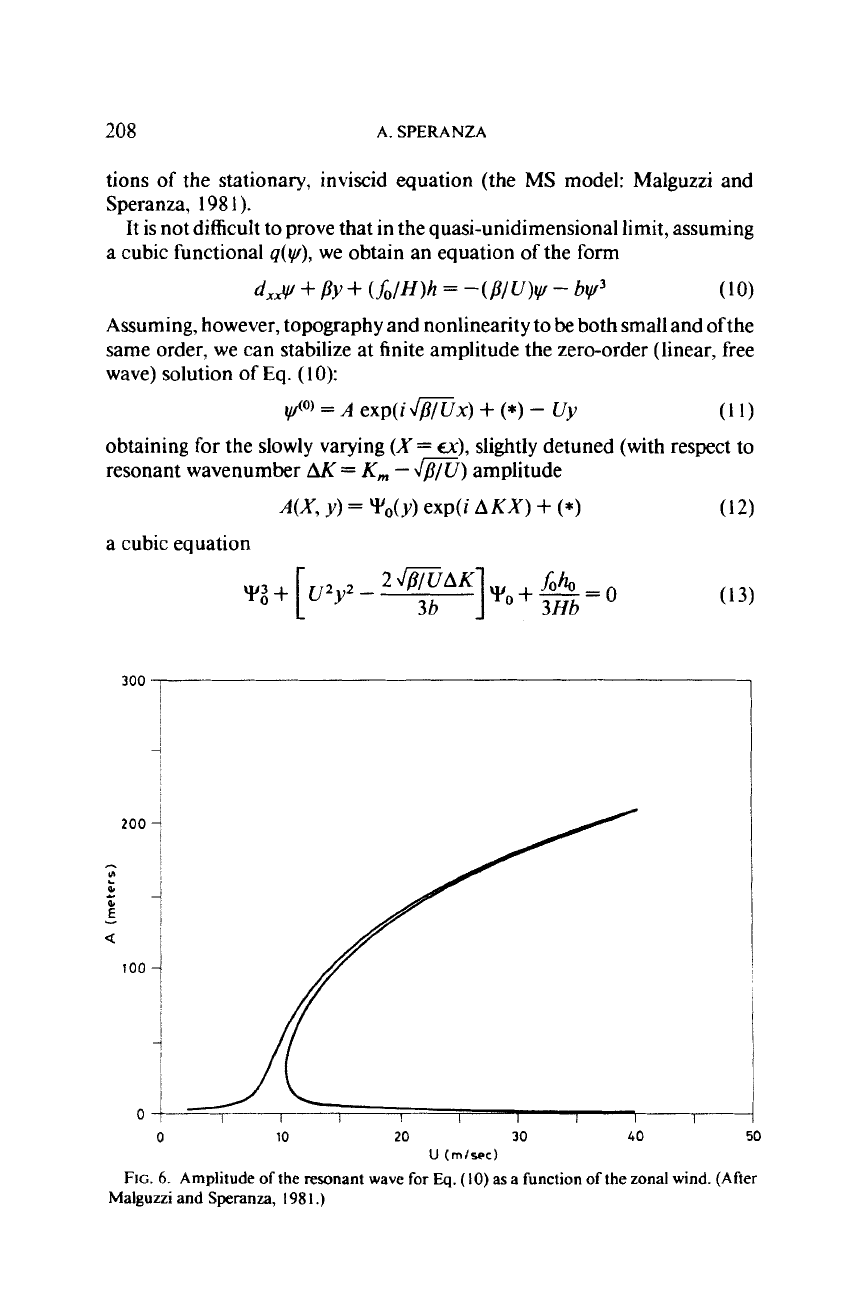
FIG. 6.
Amplitude of the resonant wave for
Eiq.
(10)
as
a function of the zonal wind. (After
Malguzzi and
Speranza,
198
I
.)

PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
209
which can easily be solved by giving the type of bending shown in Fig.
6.
The
MS
model, however, is inadequate for direct incorporation into the
CDV
scheme since it is essentially inviscid. In this
case,
in fact, the wave
component out of phase with respect to topography is identically zero. The
form-drag relationship
Eq.
(4) for zonal wind has consequently no projec-
tion on the parameter space shown in Fig.
6.
In the next section, we shall see how we can produce
a
theory which
incorporates the realistic features of both
CDV
and
MS
and produces the
right statistics in the theoretical framework of Benzi
et
al.
(
1984a).
3.
MODIFICATION
OF
THE
CDV
WAVE EQUATION
Before proceeding with the necessary modification of
CDV,
it is useful to
consider briefly the nature of the different nonlinearities appearing in the
quasi-geostrophic equations.
As
we have seen, the
CDV
nonlinearity, characterizing the feedback on
zonal momentum of mountain waves, produces a folding of the surface of
equilibrium wave amplitude in the
U*
direction in parameter space, but not,
as required by observed data, along the
U
axis. The nonlinearity of the
functional in the inviscid barotropic equation, discussed in the previous
section, produces folding in
U,
but only of the wave component in phase
with respect to topography.
Nonlinearity of the Jacobian operator has two distinct parts: wave
-
wave
interaction and wave -zonal flow interaction. The latter has very frequently
been considered in theoretical studies (see, for example, Pedlosky, I98 I),
while the former has usually been neglected. This
is
because, in the usual
one-wave representation of the wave field near neutral stability
as
an eigen-
function of the Laplace equation, direct wave self-interaction vanishes. In
the following theoretical treatment of equilibrium solutions of the baro-
tropic equation (Benzi
et
al.,
1984b), however, we prefer to consider
as
basic
nonlinearity (that bends the resonance in the
B,
Uplane) the self-interaction
of waves. Here again, ofcrucial importance is the choice of the eigenfunction
in terms of which the streamfunction field is written: our choice is that of
separated modes of the form
A(x,
t)g(y)
with a latitudinal structure such as
to guarantee wave self-interaction. In mathematical terms, we expand the
barotropic wave equation with dissipation in terms of functions of the form

2
10
A.
SPERANZA
6
=
(Sl
glyglyv)
The nature
of
the coefficients defined in
Eq.
(
16)
clarifies the meaning of the
preceding remarks concerning nonlinearity in our model. This nonlinearity
depends on the latitudinal structure of the modes: it would vanish for an
eigenfunction
of
Laplace operator of the kind considered by Pedlosky
(1
98
1)
and many others. It can
be
proved (Speranza
el
al.,
1985) that inclusion
of
local- topography, for example, is able to produce, in the quasi-neutral
modes, the latitudinal structure needed to produce self-interaction. The
ordering of parameters that turns out to be necessary
for
bending the reso-
nance in
CDV
parameter space is
(E
is a small parameter)
h=O(E);
6-€8
ho
=
O(d);
ho
-
ho€2
(17)
1'
=
O(E2);
v
-
VIE2
which, in physical terms, means that Jacobian interaction is stronger than
topographic action and frictional dissipation.
Introducing long time and space scales
T
=
E2t;
X
=
e2t
(18)
(19)
and assuming the amplitude of the wave mode is
of
the
form
A,@,
x,
t,
T)
=
A'O)(x,
x,
T)
+
€A(')
we obtain3, from
Eq.
(14),
at
zero
order in
E
(U,
4-
+
UAg
=
0
The solution of Eq. (19) is
'
Notice that we substitute here
6
-
&,
h,
-+
h&2,
and
v
-
vd
according
to
Eq.
(I
7).

PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
21
1
where
K,Z
=
(Ua
+
p)/U
that is a modified wavenumber of the stationary Rossby wave [Eq. (20)].
At first order in
E,
we obtain
(p
+
Ua)A$)
+
UAE
+
A?)
=
0
(23)
A
particular solution of Eq. (22) is
SIB(2
6(Bf
exp(i2KSx)
A(')
=
--
-
p
+
aU
2[(p
+
Ua)
-
KfU]
At the second order in
E,
secular terms appear and the consequent solution
condition reads:
=
-~(d
-
Kf)B
(25)
The introduction of slight detuning
A
K
=
K,,,
-
K,
allows us to write
h(X)
=
ho
exp(i
AKX)
+
(*)
(26)
which, introduced into Eq.
(24),
gives the stabilization equation
=
-
v(a2
-
Kf)B
(27)
The stationary version of this equation
is
a cubic condition, similar to that
of Eq.
(
13) of the preceding section, which produces resonance bending in
the
CDV
parameter space (as shown in Fig.
7).
Although the expansion
outlined above is based on
ad
hoc
assumptions, the phenomenology of
resonance bending it describes is very robust and can easily be observed in
many physical systems. Moreover, with particular reference to the baro-
tropic equation, such phenomenology is confirmed by numerical experi-
ments with both finite-difference (Rambaldi and
Mo,
1984)
and spectral
(Legras and Ghil,
1983)
models
of
very high spatial resolution. Figure
8
shows, for example, the shape of a nonlinear resonance appearing in the
stationary solutions obtained by Legras. Since Legras resonance
is
in the
wave energy-zonal energy space, it must
be
compared to our resonance in
an analogous parameter space (Fig. 8b). The similarity
is
obvious. Also,
Rambaldi's results for barotropic flow in a channel confirm the fact that the
solutions identified by means of perturbation techniques are good approxi-
mations or real solutions to the full field equations.
A
thorough analysis
212
A. SPERANZA
300
I
0
10 20
30
40
50
U
(rnlsecf
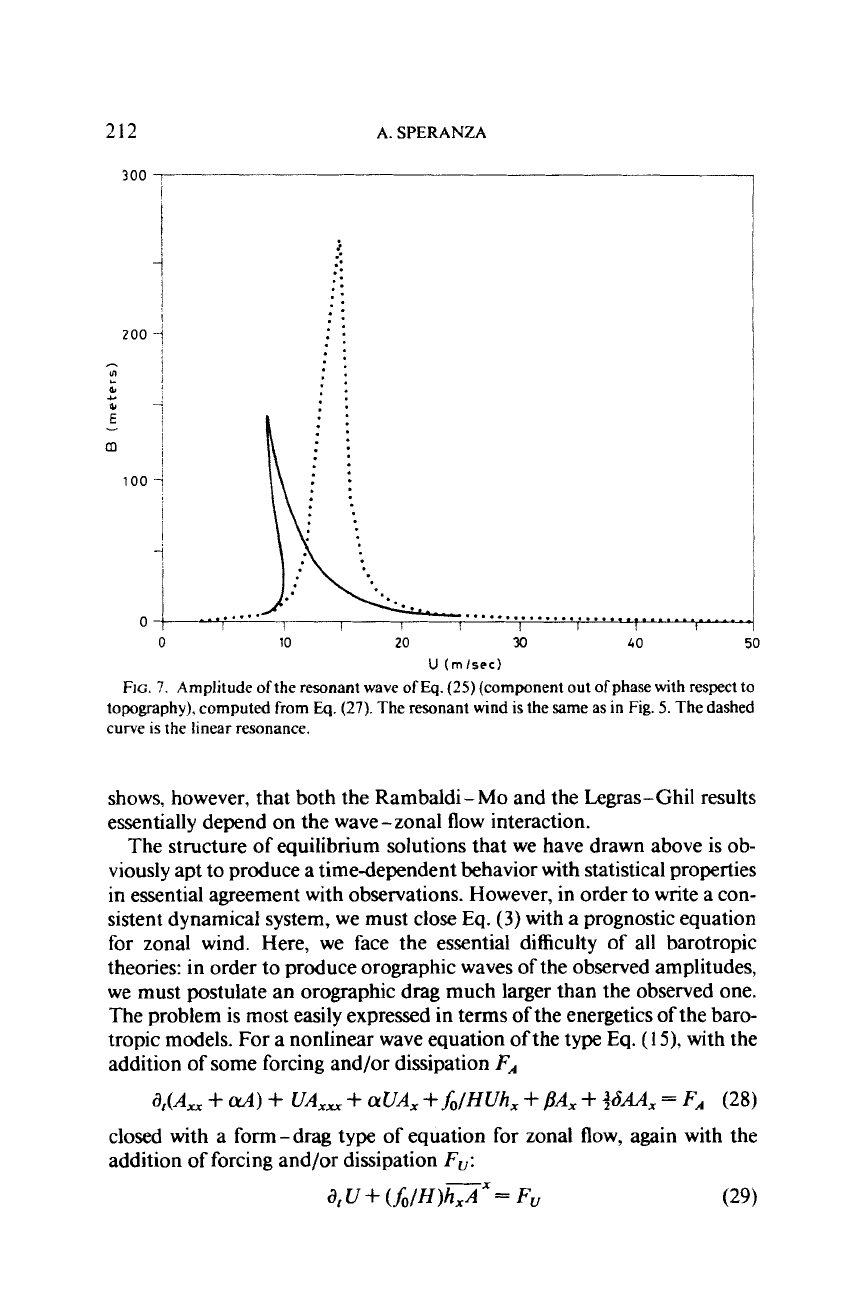
FIG.
7.
Amplitude
of
the resonant wave
of
Eq.
(25)
(component out ofphase with respect
to
topography), computed
from
Eq.
(27).
The resonant wind
is
the same as
in
Fig.
5.
The dashed
curve
is
the linear resonance.
shows, however, that both the Rambaldi
-
Mo
and the Legras-Ghil results
essentially depend on the wave
-
zonal flow interaction.
The structure
of
equilibrium solutions that we have drawn above is ob-
viously apt to produce a time-dependent behavior with statistical properties
in essential agreement with observations. However, in order to write a con-
sistent dynamicat system, we must close
Eq.
(3)
with a prognostic equation
for
zonal wind. Here, we face the essential difficulty
of
all barotropic
theories: in order to produce orographic waves
of
the observed amplitudes,
we must postulate an orographic drag much larger than the observed one.
The problem is most easily expressed in terms of the energetics
of
the baro-
tropic models.
For
a nonlinear wave equation
of
the type Eq.
(1
5),
with the
addition
of
some forcing and/or dissipation
FA
a,(A,
+
aul)
+
UA,
+
~UA,
+&/Hu~,
+PA,
+
+sax
=
F”
(28)
closed with a form-drag type
of
equation
for
zonal flow, again with the
addition of forcing and/or dissipation
F,:
a,
U
+
(&/H)hTX
=
Fu
(29)

PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
213
we obtain the energy equations
CI
0
0.04
(
0.03(
p
0.02(
0.01(
0
00
O
0
O0
oo
0
oo
0
oo
ooo
O
I
I
I
1
I
I
I
I I
I
t
0.004
0.008
0.012
0.016
0.020
I
I
I
I
I
t
f
.
.
.
.
.
.
.
.
.
.
0
0
0
0
0
0
0
0
0
.
.
.
FIG.
8.
(a) Equilibrium solutions ofthe barotropic model on the sphere of
Legras;
the energy
of the states is plotted against a nondimensional measure of zonal forcing (from
Legras
and
Ghil,
1983).
(b)
Total amplitude of the resonant wave of
Eq.
(25)
as a function of zonal wind.
