Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking
Подождите немного. Документ загружается.

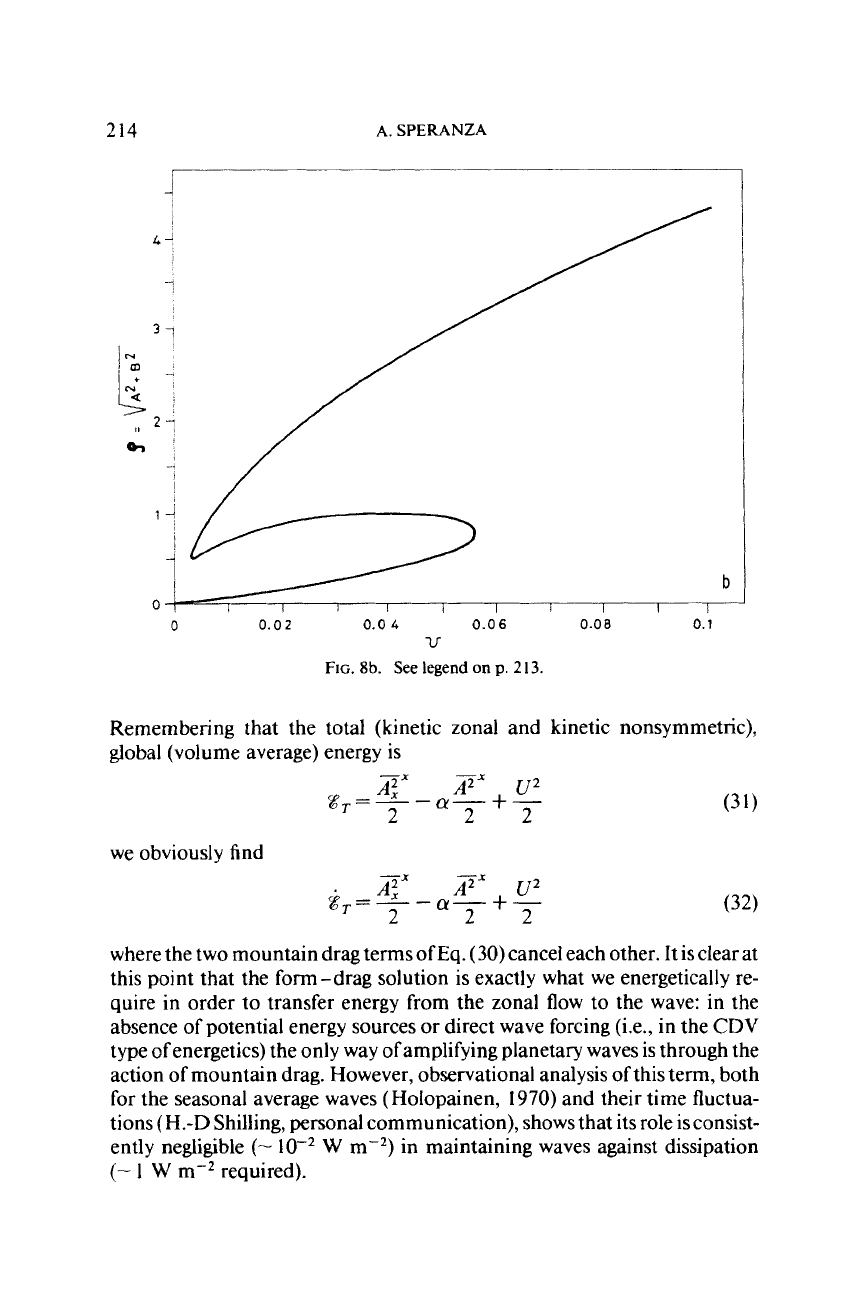
214
A.
SPERANZA
b
I
I
I
I
I
I
I
0
0.02
0.0
4
0.06
0.08
0.1
U
FIG.
8b.
See
legend
on
p.
213.
Remembering that the total (kinetic zonal and kinetic nonsymmetnc),
global (volume average) energy
is
-
-
AZx A2*
U2
8
=--a-+-
T2 22
we obviously find
where the two mountain drag terms ofEq.
(30)
cancel each other. It is clear at
this point that the form-drag solution is exactly what we energetically re-
quire in order to transfer energy from the zonal flow to the wave: in the
absence of potential energy sources
or
direct wave forcing (i.e., in the
CDV
type
of
energetics) the only way
of
amplifying planetary waves
is
through the
action of mountain drag. However, observational analysis of this term, both
for the seasonal average waves (Holopainen,
1970)
and their time fluctua-
tions (H.-D Shilling, personal communication), shows that its role is consist-
ently negligible
(-
W
m-2) in maintaining waves against dissipation
(-
1
W
m-2
required).

PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
215
More recent analysis
of
winter data in general by Chen
(1982)
and Chen
and Marshall
(
I984),
and, more specifically, of blocking versus nonblocking
cases by
A.
Hansen and H.-D. Shilling (both of which see in this volume)
confirm the above results, together with the general observation that the
source of energy for low-frequency variations
(
10
to
40
days) of the ultralong
waves is available potential.
However, the conclusion must not be drawn here that the mountain drag
term does not play an important role in the real atmosphere.
As
we shall see
in the next section, form -drag can operate as an essential catalyst for baro-
clinic conversion, although it directly forces only irrelevant amounts of
energy in the ultralong waves.
4.
BAROCLINIC ENERGETICS
The barotropic model has served well the purpose
of
isolating the mecha-
nism of nonlinear stabilization required to produce theoretical multiple-
equilibrium states in the observed variability range of Northern Hemisphere
circulation. However, as we have seen, the energetics of the observed varia-
bility is dominated by baroclinic conversion. We shall now attempt to out-
line here how to extend the concepts concerning nonlinear stabilization to a
baroclinic model atmosphere. For mathematical convenience we make use
of
the quasi-geostrophic, two-level model in the standard formulation (Ped-
losky,
1964):
where
F,
and
F2
represent any kind
of
forcing and/or dissipation and we have
assumed
F,
=
F2
=
F.
It is useful to write Eq.
(33)
in terms ofthe barotropic
[$
=
(ty,
+
ty2)/2]
and the baroclinic
[$
=
(w,
-
y2)/2]
flow components
where
F+
=
(F,
+
F2)/2
and
Fo
=
(Fl
-
F2)/2
obviously represent forcing
and/or dissipation in the barotropic and the baroclinic flow component.

216
A.
SPERANZA
Here, again, we consider a one-wave solution
of
the form
(35)
4
=
-
UY
+
A(x,
MY)
0
=
-
my
+
B(x, t)g( y)
for flow over a mountain
h
=
h(x)g(y).
wave equation
After substitution into
Eq.
(34) and projection on
g(y),
we obtain for the
a
{
$
+
U$}
[B,,
+
(a
+
2F)B]+
PB,
+
m-(Axx
+
wl)
+
2rnFA,
dX
It
is
clear that, besides the usual linear terms of dispersion and topographic
drag, we have now nonlinear self- and mutual interaction of the barotropic
and baroclinic
flow
components. The interesting point is that such terms in
turn permit us
to
fit the observed baroclinic energetics.
To
demonstrate this,
we need to close energetically the system Eq. (36) by adding equations for the
evolution of
U
and
m.
These are, respectively, the two-level version of
the momentum equation, Eq. (4), and the equation for the time evolution
of
the average baroclinicity
dU/dt
=
-(A
-
B)hXx
+
vU*
-
VU
(37)
(1
+
2F(y2))(dm/dt)
=
(A
-
B)hxx
+
2FATX
+
vm*
-
VWI
(38)
where we have assumed that linear friction and forcing are operating on the
zonal flow components. It is now interesting to compute specifically the total
energy
of
the system Eqs. (37) and
(38).
The total energy density can be
written in terms of the barotropic and baroclinic flow components,
(39)
e(x, y)
=
t(4f
+
4;
+
0:
+
0;)
+
2F02
which, once expressed in terms of the one-wave solution Eq. (35) and inte-
grated over latitude, becomes
1
U2
1
+
2F(y2)m2
2
a(x)
=
e(x,
y)
dy
=
-(A:
+
B:)
+
-
+
I
2 2
a
-
-(A2
+
B2)
+
FB2
(40)
2

PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
217
The global energy is the integral in longitude of
(x):
-
A;+
BiX
UZx
+
1
-I-
2F(y2)X
m2
2
+2
2
E=
8(x)dx=
I
The time derivative ofthis quantity can
be
recovered from Eqs.
(32)
and
(33)
by multiplying respectively by
A,
B,
U,
and
M
and integrating over longi-
tude:
-I-
2mFA3'
=
(F,g)Bx
--=-
dU2X
U(A
-
B)hxx
+
vU*U
-
vU2
2
dt
I
-I-
2F(y2)
--
dm2
-
m(A
-
B)hx"
-
2FmATx
+
vm*m
-
vm2
2 dt
where contributions from nonlinear terms have obviously disappeared. By
adding Eq.
(42),
the conservation
of
Eq.
(4
I)
for unforced inviscid flow can
be checked.
Since the contributions from nonlinear terms do not appear in the global
energetics, we can discuss our problem in terms of linear orographic waves.
Assuming that dissipation is of Laplacian
form
(vs
and
vD
are respectively the
dissipation coefficients of the barotropic and baroclinic part), for the ener-
getic balance of the stationary-wave solutions of Eq.
(36),
we obtain
(U
-
rn)
h.
(A
-
B)
+
2Fmax
-
vs(AZx
-
dx)
1
2RoH2
2
where the
first
term represents orographic conversion from kinetic energy of
the zonal flow, the second term is the divergence of the latitudinal heat
flux
and is associated with the conversion of available energy of the zonal flow,
and the last two terms represent dissipation of the wave flow component.
The linearized, stationary Eq.
(36),
with the simplifying assumption
a
=
0

218
A.
SPERANZA
reads
-
2Fm.4,
=
-
v,,Bxx
If topography is sinusoidal
h(x)
=
hoeiKmx
+
(*),
wave solutions of the form
A(x)
=
A,
eiKmx
+
(*)
B(x)
=
B,eiKmX
+
(*)
(45)
have complex amplitudes:
A,
=
{h,(U
-
m)[(P
-
UK$)
+
2FU
+
iKmvD]
+
K$m)/4RoH2A
B,
=
{ho(
U
-
m)(K$+ 2F)m
-
[(p
-
KLU)
+
iKmvs])/4RoH,A
(46)
where
A
is the determinant
of
the homogeneous linear system. The corre-
sponding heat flux divergence,
-
4=A
B
='
x
[Km(AoBo*
-
A,*B,)
is essentially determined by
A.
-
/?
-
UKL
+
2FU
+
K&m
+
iK,v,
B,
(K$
+
2F)m
-
p+
KLU
+
iK,,,v,
-_
and goes to zero
as
-
-
-[P-(u-m)K$+2FU]Km~,+K,~D[-P+((i+m)K~+2Fm]
[-p
+
(U
+
m)K$
+
2FmI2
-
(KmQ2
(49)
which is clearly independent
of
h.
In fact, the conversion term
Eq.
(47)
only
depends on the dissipation
v~,~.
It
is therefore clear that regimes are possible
in the baroclinic atmosphere in which topography only fixes the structure
and the phase
of
the wave, while the maintenance against dissipation is
guaranteed by baroclinic conversion. In fact, such regimes are found in

PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
219
models that are linear in the wave field (see Charney and Straus,
1980,
p.
1
170,
for an explicit comment on this property).
5.
RESONANCE BENDING
IN
A
BAROCLINIC MODEL
ATMOSPHERE
At this stage, one may be tempted to conclude that the nonlinear bending
due to self-interaction of the wave field is not needed in the baroclinic
dynamics since the energetic problems
of
CDV
can be solved quite naturally
in the linear wave theory. Here, however, other properties come into play.
If we insist in postulating a linear wave dynamics, we deduce from stability
analysis of the solutions of the stationary problem Eq.
(44),
that the solutions
located on the subresonant side in the plane
U
-
m
are stable, while the ones
on the superresonant side are unstable (see Buzzi
et
al.,
1984,
for a discussion
of the general stability properties of linear stationary solutions). Multiple
solutions come in sets which are distributed on different sides of the reso-
nance, with the large wave amplitude ("blocked") solution always on the
subresonant side. The attracting character resulting from the stability of
subresonant states causes all trajectories in phase space to end eventually in
the blocked state (Yoden,
1983).
Again, as in the barotropic case, we are in
the situation of needing resonance bending in order to be able to locate
different equilibria on the same side of the resonance.
The extension of the ideas concerning wave self-interaction and resonance
bending to the baroclinic case is relatively straightforward, although requir-
ing a considerable amount of algebra. The full problem is discussed in detail
in a paper by Benzi
et
al.
(1985).
Here we want only to prove with a specific
example that wave nonlinearity can produce two stable states, differing very
little in zonal flow and average baroclinicity, both stable with respect to
orographic baroclinic instability.
For this purpose it is convenient to consider the baroclinic Eqs.
(36)
-(38)
in the layer version,
4L41XX
+
F(A2
-
A,)]
+
UlAkXx
+
PAlx
+
F(UlA2x
-
WIX)
at[ALrx
+
F(A1
-
A2)I
+
U2A,
+
PA2x
+
F(UzA,x
-
UIA2x)
-
dAIAk=
-VA,,
-
6A2Ah
+
Uzh,=
-vA,
(50)
-
d,U=-Azhxx-
v(U-
U*)
--
cdfm
=
~FA,A,,~
+
~~h~~
-
v(m
-
m*)
where we have introduced a Laplacian friction with equal relaxation time
I/v
in all the processes and defined the constant
C
=
1
+
2F(
Y2).

220
A.
SPERANZA
Since we want to produce solutions that are characterized by small inter-
action with topography, we shall assume that the topographic term
U,h,
is
small. In analogy with the barotropic case we will also assume the nonlinear
and frictional terms to be small. Since we are dealing with small fluctuations
around equilibrium we assume also time derivatives to
be
small. We will also
introduce a slow space modulation in order to balance secularities in the
expansion.
The exact ordering
of
the perturbative terms that produces the balance we
are interested in comes out
to
be
as follows:
First-order small quantities: nonlinearity
s=O(E)
6-SE
Second-order small quantities: dissipation, flow in the lower layer,
slow
space modulation. slow time modulation
v
=
0(€2)
c:
=
qE2)
x2
=
€2x
7
=
E2t
v
-
VE2
u2
-
U2E2
A
zero order in the small quantities we obtain:
This is the equation
for
a stationary, free Rossby wave confined in the upper
layer that we will assume
of
the form
A\')
=
a(~,
t)eifi
+
(*)
(52)
where
X
is
the slow space scale and
K,
=
number.
is the "resonant" wave-
At first-order, nonlinearity affects the structure
of
the Rossby wave:
exactly as in the barotropic
case
[see
Eqs.
(23)-(24)].
dissipation, and flows in the lower layer) enter the picture:
At the second order, the other terms (time and slow space modulation,
dZ(A$zx
-
FA\")
+
ugA\o?,
+
/?A\:
+
3UlA\?xx
+
+
F(
u1&)
-
u
A@))
-
6A\')A\?
-
&4(O)A(')
=
2
Ix
I
Ix
-vA,x,
(54)
Fi,A\')
+
BA$?J
+
F(U2AG
-
UIA$)
+
U,hx
=
0

PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
22
I
Remembering that we are dealing with sinusoidal topography
h= ho
&K,,,x
+
(*)
and defining a deturning parameter
A
K
=
K,
-
K,,
we obtain
from the conditions of solvability of Eq.
(54)
the following form
of
the
equation for the modulation
a(X,
t)
of the quasi-stationary wave Eq.
(52)
[the wave amplitude in the lower layer can be computed explicitly from that
in the upper layer by means of the second equation of Eq.
(54)]:
The stationary version of Eq.
(55)
is a cubic that gives three solutions in
certain parameter ranges.
After solving Eq.
(55)
for
a,
the corresponding values
of
flows in the lower
layer and average baroclinicity can be deduced respectively from the second
part
of
Eq.
(54),
the form -drag and the average baroclinicity equations. One
specific example, corresponding to realistic values ofthe variables, is listed in
Table I1 together with the barotropic limiting Case
m
=
0.
It can
be
noticed
that in the solution with
m
variable amplitude of the wave field changes
appreciably (the order of magnitude is
100
geopotential meters), while the
variation
of
the zonal flow
U
and the average baroclinicity
m
remain con-
fined (the order of magnitude in
1
m sec-') as in the linear case of the
preceding section.
In the barotropic limit
rn
=
0,
a similar change ofwave amplitude requires
a much larger change in the zonal flow (order of magnitude
10
m sec-') as
discussed in Section
3.
It is interesting now to analyze the stability of the
equilibrium states computed with the aid of the nonlinear Eq.
(55).
In order to substantiate
our
qualitative remarks at the beginning of this
section, it will suffice here to consider the inviscid limit. The matrix of linear
TABLE 11. PARAMETERS
AND
VARIABLES
OF
MULTIPLE STABLE STATIONARY
SOLUTIONS
OF
THE
NONLINEAR WAVE
EQ.
(55)
(m
sec-1)
(m
sec-l)
(m
sec-I)
(m
sec-I)
(m
X
100)
(m
X
100)
equilibrium
Baroclinic
state
(m*
=
15.0
m
sec-l)
23.8
15.0
21.0
14.0
1.14
+
i0.40 0.34
+
iO.l
I
Blocked
23.8
15.0
23.8 14.9
-0.17
+
i0.006 -0.02
+
i0.002
Zonal
Barotropic
state
(m
=
0)
40.6
15.0
21
0
2.14
+
i0.41 4.28
+
20.78
Blocked
40.6
15.0
40.5
0
-0.32
+
i0.004
-0.29
+
i0.06
Zonal
U*
m*
.
U
m
A, A*
Type
of

222
A.
SPERANZA
perturbation of our dynamical system is
O1
-(QU2
+
28
Ak)
-
3Ks6af
-
L
-
2HQKP
-
2
u2QHK
f
lP
-0
where we have defined
Q
=
K:F/(K:
-
F),
H
=
h,-,/Kf,
and
cr
is the eigen-
value
of
the linear perturbations (assumed proportional to
em).
Notice that
only the wave and form
-drag
equations have been perturbed since
dmldt
is
constant in the orographic baroclinic instability (see Buzzi
et
al.,
1984).
Note
also that only the real part of the stationary wave solution
(a,)
appears since
in the inviscid limit the imaginary part vanishes
(ai
=
0).
The dispersion relation derived from the vanishing of the determinant of
Eq.
(56)
can be written in the form
(57)
where use has been made
of
the fact that
a,
must be a stationary solution of
the nonlinear problem, Eq.
(55).
We can analyze the stability of multiple-equilibrium solutions by taking
the limit
of
Eq.
(57)
for
a,
-
co
(large-amplitude “blocked” and “interme-
diate” states) and
a,
-
0
(the small-amplitude “zonal” state). In the limit of
large wave amplitude we obtain
M,a;
+
(QU2
+
2P
AK)a,
+
QU2H
=
0
which, for sufficiently large nonlinearity,
6
>
Q2K,21PF,
implies stability for
a,
>
0
(“blocked” branch) and instability for
a,
<
0
(“intermediate”
branch). In the opposite limit,
cr’
becomes large and positive, implying
stability. In conclusion, the stability properties are as envisaged in the begin-
ning
of
this section.
At this point, any further quantitative statement concerning the physical
processes we are dealing with must
be
based on a mathematical analysis of
the baroclinic equilibrium states and their stability properties in the presence
of resonance folding. However, whatever the physical process in question,
we expect mountain drag, even if small, to be correlated with the fluctuations
of the ultralong waves. This correlation, in fact, is observed at periods of
about
20
days as shown in
Fig.
9.
As
mentioned at the end
of
the preceding
section, the form -drag
is
too small to convert energy directly from the zonal
wind but, acting
as
a catalyst, can produce baroclinic conversion on the scale
of
topography which, in our case, is much larger than the natural scale of
“slantwise convection,” i.e., the Rossby deformation radius.
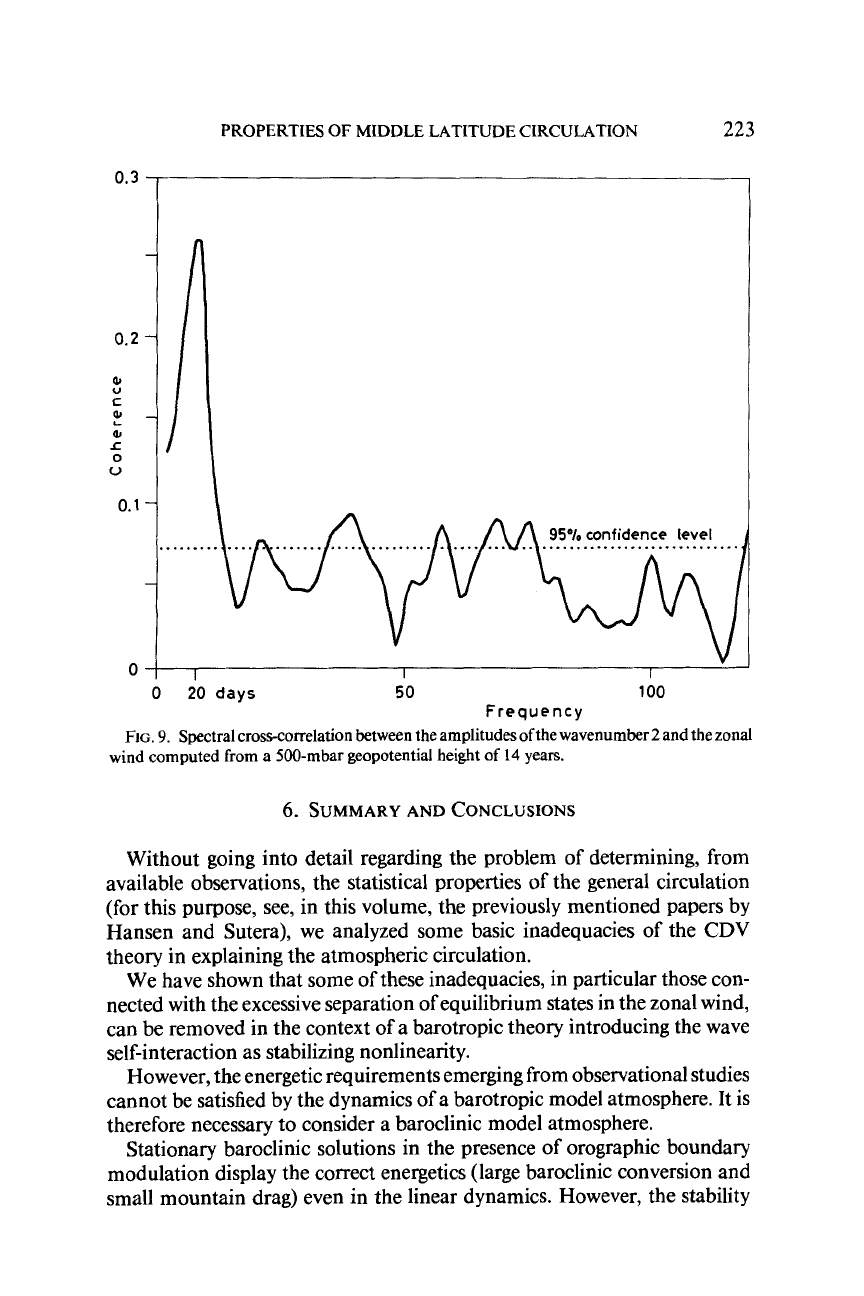
PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
223
o
20
days
0.3
0.2
0,
C
0,
c
0
V
U
:
0.1
0
~~ ~~ ~~
95%
confidence level
50
100
Frequency
FIG.
9.
Spectral cross-correlation between the amplitudes ofthe wavenumber
2
and the zonal
wind computed
from
a 500-mbar geopotential height
of
14
years.
6.
SUMMARY
AND
CONCLUSIONS
Without going into detail regarding the problem of determining, from
available observations, the statistical properties of the general circulation
(for this purpose, see, in this volume, the previously mentioned papers by
Hansen and Sutera), we analyzed some basic inadequacies of the
CDV
theory in explaining the atmospheric circulation.
We have shown that some of these inadequacies, in particular those con-
nected with the excessive separation of equilibrium states in the zonal wind,
can be removed in the context
of
a barotropic theory introducing the wave
self-interaction as stabilizing nonlinearity.
However, the energetic requirements emerging from observational studies
cannot be satisfied by the dynamics of a barotropic model atmosphere. It is
therefore necessary to consider a baroclinic model atmosphere.
Stationary baroclinic solutions in the presence of orographic boundary
modulation display the correct energetics (large baroclinic conversion and
small mountain drag) even in the linear dynamics. However, the stability
