Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking
Подождите немного. Документ загружается.


194
J.
EWER
ET
AL.
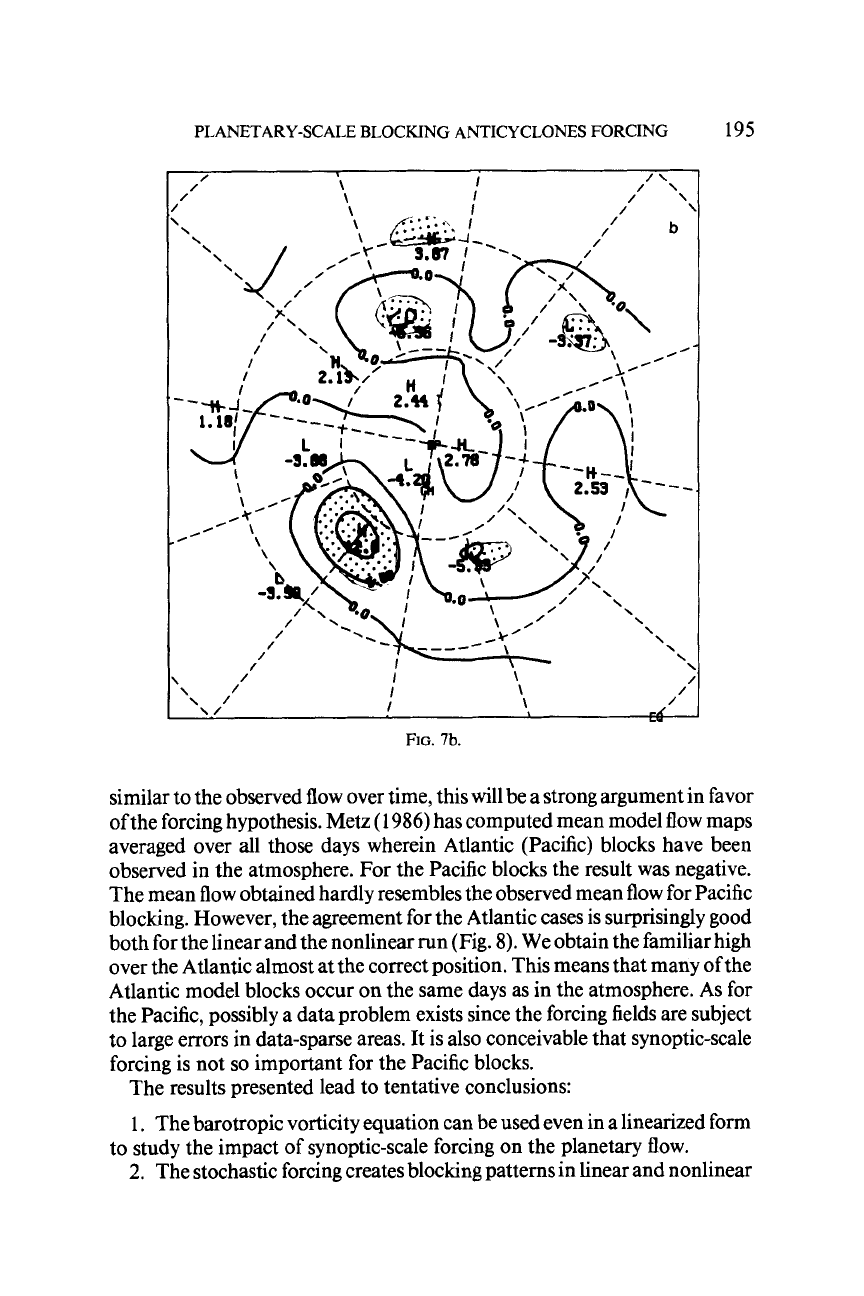
the annual cycle. To establish the typical blocking flow pattern in the model
Metz
(1
986) has computed the mean maps of the streamfunction anomalies
averaged over all Atlantic and all Pacific blocking periods separately. The
result for the Atlantic case and for the linear run is shown in Fig.
7
and is to be
compared to the corresponding map derived from the
I
1
winters. The agree-
ment is quite good, although the amplitudes are somewhat too
low
in the
modelderived map. The corresponding map for the nonlinear run is similar.
The agreement for the Pacific cases is not
so
good but is still satisfactory
(Metz, 1986). All this demonstrates that a majority of the most prominent
characteristics of atmospheric blocking are captured by the model. Strictly
speaking, this does not prove that atmospheric blocks can
be
caused by the
synoptic-scale forcing. After
all,
the flow evolution in the model is not the
same as that in the atmosphere, and the forcing acts in flow fields which are
not those observed, However,
if
we can demonstrate that the model flows are
FIG.
7.
Mean streamfunction
(
lo6
m2
sec-I) anomaly for wintertime
blocking
in
the
Atlan-
tic
(40"W
to
1O"W);
a, observations;
b,
linear model result.
Stippling:
95%
confidence area.
Adapted
from
Metz
(
1986).
PLANETARY-SCALE BLOCKING ANTICYCLONES FORCING
195
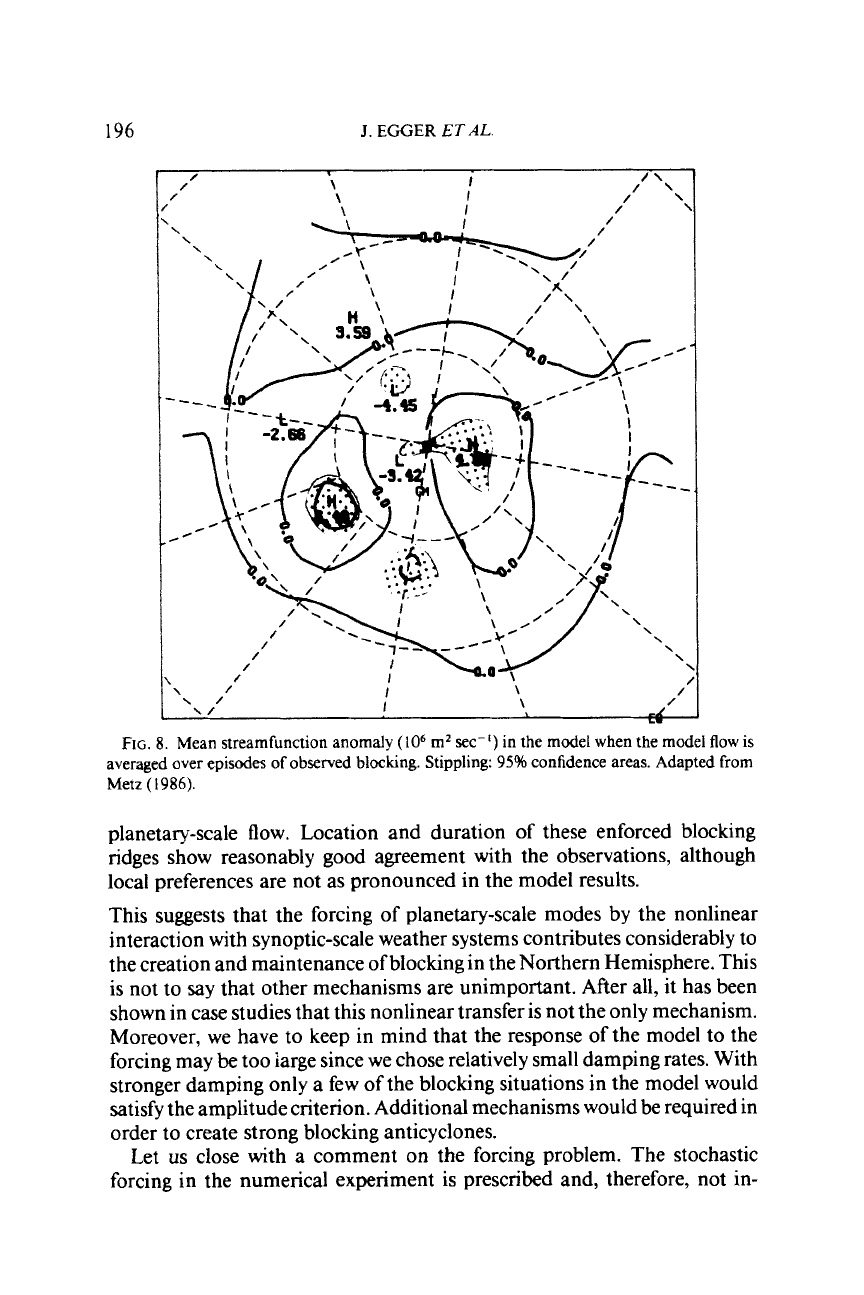
similar to the observed flow over time, this will be a strong argument in favor
of the forcing hypothesis. Metz
(1
986)
has computed mean model flow maps
averaged over all those days wherein Atlantic (Pacific) blocks have been
observed in the atmosphere. For the Pacific blocks the result was negative.
The mean flow obtained hardly resembles the observed mean
flow
for Pacific
blocking. However, the agreement for the Atlantic cases is surprisingly good
both for the linear and the nonlinear run (Fig.
8).
We obtain the familiar high
over the Atlantic almost at the correct position. This means that many of the
Atlantic model blocks occur
on
the same days as
in
the atmosphere. As for
the Pacific, possibly a data problem exists since the forcing fields are subject
to large errors in data-sparse areas. It is also conceivable that synoptic-scale
forcing
is
not
so
important for the Pacific blocks.
The results presented lead to tentative conclusions:
1.
The barotropic vorticity equation can be used even in a linearized form
2.
The stochastic forcing creates blocking patterns in linear and nonlinear
to study the impact of synoptic-scale forcing on the planetary flow.
196
J.
EGGER
ETAL
FIG.
8.
Mean streamfunction anomaly
(lo6
m2
sec-')
in the model when the model
flow
is
averaged over episodes
of
observed
blocking.
Stippling:
95%
confidence areas. Adapted from
Metz
(1986).
planetary-scale
flow.
Location and duration of these enforced blocking
ridges show reasonably good agreement with the observations, although
local preferences are not as pronounced in the model results.
This suggests that the forcing of planetary-scale modes by the nonlinear
interaction with synoptic-scale weather systems contributes considerably to
the creation and maintenance of blocking in the Northern Hemisphere. This
is not to
say
that other mechanisms are unimportant. After all, it has been
shown in case studies that this nonlinear transfer is not the only mechanism.
Moreover, we have to keep in mind that the response of the model to the
forcing may
be
too iarge since we chose relatively small damping rates. With
stronger damping only a few of the blocking situations in the model would
satisfy the amplitude criterion. Additional mechanisms would be required in
order to create strong blocking anticyclones.
Let
us
close with a comment on the forcing problem. The stochastic
forcing in the numerical experiment is prescribed and, therefore, not in-

PLANETARY-SCALE BLOCKING ANTICYCLONES FORCING
197
fluenced at all by the planetary flow in the model. In particular, the blocks in
the model are enforced by the synoptic-scale eddies but these eddies do not
“feel” the block in the model. Nevertheless, the blocking climatology of the
model has been found to be reasonably realistic. This suggests that the
influence of the planetary
flow
on the synoptic-scale forcing may be minor.
However, it would be premature to draw such a conclusion.
A
significant
interdependency of forcing and large-scale flow may be found in reality
despite the fact that the model produces reasonably realistic results with
independent forcing. This is suggested by the observed strong local prefer-
ence of the eddy forcing and by instability calculations like those
of
Fred-
eriksen
(1983).
REFERENCES
Benzi, R., Hansen,
A.,
and Sutera, A.
(1984).
On stochastic perturbation of simple blocking
Charney, J., and DeVore,
J.
(1 979).
Multiple flow equilibria in the atmosphere and blocking.
J.
Chen, T.-C., and Shukla,
J.
(1
983).
Diagnostic analysis and spectral energetics of a blocking
Colucci,
S.,
Loesch, A., and Bosart, L.
(1981).
Spectral evolution of a blocking episode and
Egger, J.
(1978).
Dynamics
of
blocking
highs.
J.
Atmos.
Scz.
35, 1788- 1801.
Egger, J.
(1 98
1).
Stochastically driven large-scale circulationswith multiple equilibria.
J.
Atmos.
Egger,
J.,
and Schilling, H.-D.
(1983).
On the theory of the long-term variability of the atmo-
Egger,
J.,
and Schilling, H.-D.
(1984).
Stochastic forcing of planetary scale flow.
J.
Atmos.
Sci.
Fischer, G.
(1984).
Spectral energetics analyses of blocking events in a general circulation
Frederiksen,
J.
(
1983).
Disturbances and eddy fluxes in Northern Hemisphere flows in stability
Green,
J.
(1
977).
The weather duringJuly
1976:
Some dynamical considerations ofthe drought.
Hansen,
A.,
and Chen, T.-C.
(1982).
A spectral energetics analysis
of
atmospheric blocking.
Hansen,
A.,
and Sutera,
A.
(1 984).
A
comparison of the spectral energy and enstrophy budgets
Illari, L., and Marshall, L.
(1983).
On the interpretation of maps
of
eddy fluxes.
J.
Atmos.
Sci.
Kalnay-Rivas, E., and Merkine, L.
0.
(198 1).
A simple mechanism for blocking.
J.
Atmos.
Sci.
Metz,
W.
(1986).
Transient cyclone-scale vorticity forcing
of
blocking
highs.
J.
Atmos.
Sci.,
models.
Q.
J.
R.
Meteorol.
Soc.
110, 393-409.
Atrnos.
Sci.
37,
1
157
-
1
176
event in the GLAS climate model simulation.
Mon. Weather
Rev.
111, 3-22.
comparison
with
wave interaction theory.
J.
Atmos.
Sci.
38,2092 -2
1
1
1.
Sci.
38,2606 -26 18.
sphere.
J.
Atmos.
Sci.
40,
1073- 1085.
41,779-788.
model. Cont.
Atmos. Phys.
57, 183-200.
of three-dimensional January and July flows.
J.
Atmos.
Sci.
40,
836-855.
Weather
32,
120- 128.
Mon.
Weather Rev.
110,
1146- 1159.
of blocking compared to non-blocking periods.
Tellus
36A, 52-63.
40,2232-2242.
38,2077 -209
1.
submitted.

198
J.
EWER
ET
AL.
Muller,
G.
(1984).
Blockierungen in einem Modell mit stochastischer Forcierung. Diplomar-
Schilling,
H.-D.
(1982).
A
numerical investigation of the dynamics
of
blocking waves in a
Schilling,
H.-D.
(1986).
On
atmospheric blocking
types
and blocking numbers.
Adv.
Geophys.
Shutts,
G.
(1983).
The propagation of eddies in diffluent jet-streams: eddy vorticity forcing
of
Treidl,
R.
A., Birch,
E.,
and
Sajecki,
P.
(198
1).
Blocking action in the northern hemisphere:
A
Tung,
K.-K,
and Lindzen,
R.
(1979).
A
theory of stationary long waves. Part
I:
A
simple theory
beit,
Meteorol Inst. Univ. Miinchen.
simple two-level mdel.
J.
Atmos.
Sci.
39,998-
1017.
29,71-99.
“blocking”
flow
fields.
Q.
J.
R.
Meieorol.
SOC.
109,
737-761.
climatological study. Atmos.
Oceun
19,
1-23.
of
bloclung.
Mon.
Weather
Rev.
107,714-734.

DETERMINISTIC AND STATISTICAL
PROPERTIES
OF
NORTHERN HEMISPHERE,
MIDDLE LATITUDE CIRCULATION:
MINIMAL THEORETICAL MODELS
A.
SPERANZA*
Consiglio
Nazionale Ricerche-
Istituto Fisica Bassa e Alta Atmodera
and Institute
of
Physics
University
of
Bologna
I-40126
Bologna; Italy
1.
INTRODUCTION
Although the notion of “weather types” is quite old in meteorology, the
physical discussion concerning the definition, interpretation, and modeling
of “anomalous” atmospheric circulations is relatively recent. The papers
which addressed the fundamental questions concerning the structure of
phase space in the atmospheric system all appeared in 1979: in a sequence of
works, Lindzen and Tung (Tung and Lindzen, 1979a,b; Tung, 1979) give a
full account of the linear theory of three-dimensional, neutral planetary
waves in the middle latitude circulation. They discussed the possible inter-
pretation ofblocking anomalies in terms of neutral Rossby waves of particu-
larly large amplitude modulated by zonal nonhomogeneities in the bound-
ary conditions (topography)
or
in the external forcing (heat sources and
sinks). Low-frequency variability was interpreted to be caused by the linear
“adjustment” of the circulation to changes in the basic zonal wind, the
evolution of which was conceived as determined by independent dynamics.
In statistical terms, the picture that emerged was that of an atmospheric
circulation performing “small” (linear) oscillations around an equilibrium
point essentially determined by the dynamics of the zonal flow (not dis-
cussed in the above-mentioned papers).
Charney and DeVore
(1
979) and Wiin-Nielsen
(1
979) studied essentially
the same linear dynamics of planetary-wave excitation by zonal nonhomo-
geneities, only with the addition of an explicit law of zonal wind time evolu-
tion in terms
of
the amplitudes of the waves themselves. Minimal trunca-
tions of the motion equations were shown to produce a more complex
structure of the phase space, characterized by the presence of different equi-
*
Most
of the
work
presented here has been performed in cooperationwith
Dr.
R.
knzi ofthe
IBM
Scientific Center
in
Rome,
Italy.
199
Copyright
0
1986
by
Academic
Press,
Inc.
All
rights
of
reproduction
in
any
form
resewed.
ADVANCES
IN
GEOPHYSICS,
VOLUME
29

200
A.
SPERANZA
librium basins. The meteorological implication
of
the presence of multiple
equilibria was suggested to be the existence of different persistent types of
atmospheric circulations.
Successive papers aimed at extending the theory to more realistic model
atmospheres (Charney and Straus, 1980; Charney
et
al.,
198
1)
showed how
the complexity of the problem increases considerably with the number of
degrees of freedom. This impression was confirmed by later papers. Rein-
hold and Pierrehumbert
(
I982), for example, extending the model of Char-
ney and Straus to include all additional baroclinic waves in the truncation,
found an aperiodic vacillation between two distinct weather regime states,
not located near any of the stationary equilibria of the Charney
-
Straus type
of truncated model.
In
view of the difficulty
of
the problem, it appears advisable to reexamine
minimal models
of
general circulation in the light of known observational
phenomenology, to
try
to organize a hierarchy of models in which the in-
crease in complexity is maintained at each step at the minimum necessary
to
represent the essential physical symmetries needed to satisfy observational
requirements.
To
begin with, we concentrate on the statistical properties of the general
circulation, leaving other properties (detailed space- time structure of
anomalies, etc.) as
a
subject of future work. In Section
2,
we reexamine some
properties of the Charney and DeVore (CDV) model which play a key role in
determining its statistical properties. In Section
3,
we propose, still within the
context of barotropic theory, some modifications of CDV theory, aimed at
clarifying several of the obscure points concerning the statistical properties
of Northern Hemisphere circulation. We discuss an extension to incorporate
baroclinity in Section
4
and in Section
5
we draw some tentative conclusions.
Observational studies regarding the statistical properties discussed here are
presented in the companion articles by
A.
Sutera and
A.
Hansen in this
volume.
2.
A
REEXAMINATION
OF
CDV
Although a number of interesting questions could
be
raised concerning
the procedure of projection and truncation
of
the barotropic equation Iead-
ing to the CDV model, we will assume this procedure known and start from
the CDV system written in the unidimensional formulation outlined by
Hart
(
1979) and extensively used by Buzzi
et
al.
(1984).
Our preference for unidimensional formalism
is
not only due to its intrin-
sic simplicity, but also to the fact that it provides us with a field theory

PROPERTIES
OF
MIDDLE LATITUDE CIRCULATION
20
1
characterized by some useful mathematical properties. In particular, the
stationary solutions of the unidimensional problem we intend to examine
are solutions of the barotropic equation. The same is not true for the station-
ary solutions of the original
CDV
system.
As
a matter of fact, this difficulty is
encountered every time, following a classical procedure, the equations of
motion are projected onto the eigenfunctions
of
the Lapiace operator. Such
eigenfunctions, in fact,
form
a complete set, but their linear combinations
are not necessarily solutions of the stationary nonlinear problem: the sta-
tionary solution of any truncated version of the projected equation is not, in
general, a solution of the original stationary problem.
In the case of unidimensional formalism, on the other hand, we shall deal
with stationary solutions that are solutions of the full barotropic equation.
This property may prove to
be
crucial to an appropriate representation of
localized (soliton type) solutions.
Given these premises, we proceed with the analysis of the unidimensional
CDV
model. Topography
is
assumed to be of the form
h(x)
=
cos
K,x
(1)
The streamfunction is composed of a uniform zonal flow plus a wave of the
same shape as the topography:
~(x,
t)
=
-
U(t)y
+
A(t)
cos
Kmx
+
B(t)
sin
Kmx
(2)
The wave is maintained by zonal flow over the topographic slope and dissi-
pated by friction:
k
+
(V/K,)A
+
(U
-
/3/K&)B
=
0
B-(U-/3/KZ,)A+(v/Km)B+(f,h,/K~H)U=O
(3)
and the zonal flow is forced by some momentum convergence mechanism
U*,
dissipated by linear friction, and accelerated or decelerated by mountain
drag:
U-
(f,hoK,,,/4H)B
-
v(U
-
U*)
(4)
Equilibrium solutions
of
Eqs.
(3)
and
(4)
can be found easily by solving the
linear system [Eq.
(3)]
for
B
(the amplitude
of
the wave component out
of
phase with respect to topography) as a function of
U
and by searching for the
intersection of the resulting curve
B(
U)
with the linear relationship corre-
sponding to the stationary version of
Eq.
(4),
as shown in Fig.
1.
Once the appropriate points in the plane B,Uare selected,
A
is
also deter-
mined along the curve
A(
U).
By
means of stability analysis, equilibrium
E,
was identified by
CDV
as zonal,
E2
as blocked, and the third,
E,,
as an
intermediate equilibrium, unstable with respect to a new kind of instability,

202
A.
SPERANZA
300
1
I
--
OW,
0
10
LO
50
U
(rnlsec)
2o
\
30
FIG.
1.
Out-of-phase amplitude ofthe resonant wave for the onedimensional model,
Eq.
(3).
The amplitude is expressed in meters and the resonant wind is about
12
m sec-I. The straight
lines in the figure represent the stationary versionofthe form-dragequation, Eq.
(4),
asinCDV
for different value of the momentum forcing. The
E,,
E2,
and
E,
are stationary (respectively
“zonal.” “blocked.” and “intermediate”) solutions.
named “orographic” because of the role played
in
its growth by the orogra-
phic drag action appearing in Eq.
(4).
It is clear that the presence of multiple equilibria is due to a simple folding
of
the state surface in the direction
U*
in parameter space. Although the
physics is simple and interesting, one already notices some of the theory’s
inadequacies, even at this early stage. First, not all the locations of the
equilibria along the
U
axis are realistic’: this zonal flow corresponds to
speeds which are never observed in the real atmosphere (we shall return to
this point later). Moreover, the phase of the blocked wave is negative
(troughs over ridge), again, against observational evidence. Such distortions
of
the observed dynamics can perhaps be tolerated in such a simple model.
However, even more serious inadequacies are found in the statistical proper-
ties of the
CDV
model atmosphere.
Notice that in Fig.
I
the slope in the B,G’plane of“form-drag” relationship Eq.
(4)
exceeds
by
a
factor
of4
that ofCDV becauseofthedifferent choiceoflatitudinal zonal flow shape and is,
therefore, already improved with respect to the original
CDV
formulation.

PROPERTIES
OF
MIDDLE
LATITUDE
CIRCULATION
203
Given the equilibrium structure of phase space illustrated in Fig.
I,
it is
obvious that the asymetric time behavior of the time-dependent system
[Eqs.
(3)
and (4)] is characterized by only two possibilities: orbits in phase
space can, in a certain span of time, die either in
E,
or in
E,.
In order to
produce transitions between zonal and blocked states, we have to superim-
pose on the stationary solution some sort of perturbation. This can be done
by
increasing the dimensionality of the model or, more simply,
by
taking
into account the effects
of
small random noise on the deterministic CDV
dynamics. This was done
by
Egger (198 l), who integrated numerically the
Fokker-Plank equation for the evolution
of
probability density in phase
space
of
the stochastically perturbed CDV system; Egger obtained the intui-
tive result that the asymptotic statistics of occupation
of
states in the CDV
system are characterized by maxima centered at the stable equilibria. The
same problem was also studied by Benzi et
al.
(1984a), with an analytic
technique for estimating the expectation values of exit times. From the
potential wells of the CDV theory, use of this analytical technique, instead
of
numerical integration, makes the overall picture
of
the model’s statistical
properties more controllable.
The estimate is based on the assumption
l/v
<<
I/€
(5)
where
l/v
is the time typical
of
dissipative processes and
I/E
is the time scale
of random noise.
In the limit Eq.
(5)
it can be proved that the behavior ofthe entire system is
approximated by the single stochastic differential equation for the zonal
wind:
dU=
-(dV/dU)
dt
+
cl/’
dW
(6)
where
V(
U)
is the equivalent ofa potential for the motion of perturbed CDV
system in the phase space, and Wis a Wiener process with amplitude
E’/~.
The potentials are shown in Fig.
2.
The corresponding stationary probability
density is
P(
U)
=
N
exp
[
-
2
V(
U)/E]
(7)
where
N
is a normalization constant.
Figure
3
shows the probability distributions corresponding to the poten-
tials of Fig.
2.
In the limit
of
E
-+
0,
the expectation values
E[
]
of the exit
-
V”(
U3)1-’/’
exp(2
A
,
V/E)
-
V”(U3)[-1’2
exp(2
A,V/E)
and
A,V=
V3
-
V,,
A,V=
V3
-
V,,
(8)
