Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking

Подождите немного. Документ загружается.

224

SPERANZA

properties of multiple baroclinic equilibrium states obtained with a linear

resonance theory (as in Charney and Straus,

1980)

are not of the type re-

quired: the only state stable with respect to orographic baroclinic instability

the subresonant (“blocked”) state where the minimal dynamical is ulti-

mately bound

reside independently of the initial condition.

The same concepts (resonance folding due to wave self-interaction, etc.)

that appear of

key

importance in allowing the fitting ofthe observed statistics

in the barotropic

case

can

applied to baroclinic models by means of

straightforward, albeit somewhat lengthy, calculations. In such a model the

mountain forcing does not play a direct role but acts only as a symmetry-

breaking boundary modulation, catalyzing baroclinic conversion at ultra-

long wavelengths.

Introduction of wave nonlinearity in the minimal baroclinic system

allows not only production of multiple-equilibrium states (which, although

differing appreciably in wave amplitude, are confined within a limited range

of variation

mean momentum and baroclinicity), but also adjustment

(through resonance bending) the stability properties to the required charac-

teristics of stability: two stable extreme states and one intermediate, unstable

state with respect to orographic baroclinic instability.

Such considerations are not intended to signify that the type of minimal

systems just sketched can exhaust the problematics of low-frequency varia-

bility. Many more problems have to be faced, in particular those connected

with the interaction of ultralong waves with synoptic-scale disturbances.

However, we think we have enough evidence to conclude that the full

range of nonlinear effects has yet to

thoroughly analyzed and that these

effects should

further studied before they are used to draw final conclu-

sions about what goes under the name of “multiple-equilibria theory.”

REFERENCES

Benzi,

R.,

Hansen, A.

R.,

and Sutera,

(1984a).

stochastic perturbation ofsimple blocking

models.

Meteorol.

Soc.

110,

393-409.

Benzi,R.,

MaIguzzi, P., Speranza,

A.,

and Sutera,

984b). On the theory ofstationary waves

and blocking.

Meteorol.

Soc.,

July.

Benzi.

R.,

Speranza,

A.,

and Sutera,

(1985).

minimal baroclinic theory of low-frequency

variability

the Northern-Hemisphere.

Almos.

Sci..

submitted.

Buzzi,

A,,

Speranza,

A..

and Trevisan,

(1984). Instabilities of a baroclinic flow related

topographic forcing.

Atmos.

Sci.

41,637-650.

Charney,

G.,

and DeVore,

(1979). Multiple flow equilibria in the atmosphere and

blocking.

Atmos.

Sci.

36,

1205-

16.

Charney.

G.,

and Straus,

M. (1980). Formdrag instability, multiple equilibria and propa-

gating planetary waves in baroclinic, orographically forced, planetary wave systems.

Atmos.

Sci.

31,

1157-

1176.

PROPERTIES

MIDDLE LATITUDE CIRCULATION

225

Charney,

G.,

Shukla,

J.,

and Mo, K. C.

(1981).

Comparison ofa barotropic blocking theory

Chen,

(1982).

further study of spectral energetics in the winter atmosphere.

Mon.

Chen,

C.,

and Marshall,

(

1984).

Time variation of atmospheric energetics in the FGGE

Egger,

1).

Stochastically driven large-scale circulation with multiple equilibria.

Atmos.

Hart,

(1979).

Barotropic, quasi-geostrophic flow over anisotropic mountains.

Atmos.

Holopainen, E.

(1970).

An observational study of the energy balance of the stationary

disturbances in the atmosphere. Q.

R. Meteorol.

Soc.

96,626 -644.

Legras, B., and Ghil, M.

(1983).

Blocking and variations in atmospheric predictability.

“Predictability of Fluid Motion”

(G.

Holloway and B.

West, eds.). American Inst. of

Physics,

106.

Malanotte Rizzoli, P., and Malguzzi, P.

(1984).

Nonlinear stationary Rossby waves over non-

uniform zonal winds and atmospheric blocking. Part

The analytical theory.

Atmos.

Sci.

41,2620-2628.

Malguzzi, P., and Speranza, A.

1).

Local

multiple equilibria and regional atmospheric

blocking.

Atmos.

Sci.

38,

1939- 1948.

Pedlosky,

(1964).

The stability

currents in the atmosphere and the ocean. Part

Atmos.

Sci.

21, 201-219.

Pedlosky,

(1981).

Resonant topographic waves in barotropic and baroclinic flows.

Atmos.

Sci.

38,2626-2641.

Pierrehumbert, R.

T.,

and Malguzzi, P.

(1984).

Forced coherent structures and local multiple

equilibria in a barotropic atmosphere.

Atmos.

Sci.

41,246-257.

Rambaldi,

S.,

and Mo, K. C.

984).

Forced stationary solutions in a barotropic channel:

Multiple equilibria and theory of non-linear resonance.

Atmos.

Sci.

41,3 135-3146.

Reinhold, B. B., and Pierrehumbert, R. T.

(1982).

Dynamics ofweather regimes: Quasi-station-

ary waves and blocking.

Mon. Weather Rev.

110,

1105-

1145.

Speranza, A.,

Buzzi,

A., Trevisan, A., and Malguzzi, P.

(1985).

theory ofdeep cyclogenesis in

the

lee

of the Alps: Modifications of baroclinic instability by

localized

topography.

Amos.

Sci.

42, 1521

1535.

Tung,

K.,

and Lindzen, R.

(1979a).

theory of stationary long waves. Part I:

simple

theory

of blocking.

Mon. Weather Rev.

107,714-734.

Tung,

K.,

and Lindzen, R.

(1979b).

A theory of stationary long waves. Part 11: Resonant

Rossby waves in the presence of realistic vertical shears.

Mon. Weather Rev.

107,735

750.

Yoden,

(

1983).

Nonlinear interactions in a two-layer, quasi-geostrophic, low-order model

with topography.

Meteorol.

Soc.

Jpn.

61,

18.

Wiin-Nielsen, A.

(1979).

Steady states and stability properties of a

low

order barotropic system

with forcing and dissipation.

Tellus

31, 375-386.

with observation.

Atmos.

Sci.

38,762-779.

Weather Rev.

110,947-961.

winter.

Tellus

36A,

25 1-268.

Sci.

38,2606 -26 18.

Sci.

36, 1736

1746.

This Page Intentionally Left Blank

PROBABILITY DENSITY DISTRIBUTION

LARGE-SCALE ATMOSPHERIC FLOW

ALFONSO

SUTERA

The Center for Environment and

Man

Hartford, Connecticut

061

17,

and

Department

Geology and Geophysics

Yale University

New Haven, Connecticut

0651

INTRODUCTION

Whether the large-scale atmospheric motion undergoes temporal varia-

tions about more than one dynamical regime is a question with both theoret-

ical and practical relevance. In fact, if we suppose that more than one regime

occurs, then the mean state of the atmosphere would not be adequately

represented by its long-term average, but rather by the set

average states

obtained by considering, separately, each individual regime. As another

consequence of this hypothesis, it is apparent that transition from one re-

gime to the others would be conditioned by the initial state,

that long-term

forecasts would be more strongly dependent on initial conditions than in the

case in which one single mode occurs (Moritz and Sutera, 1981; Leith,

1978). This question has received more renewed attention recently since

simple models (for instance Charney and DeVore, 1979)

atmospheric

motions have shown the possibility that more than one equilibrium regime is

consistent with the equations considered. Efforts to connect these theoretical

studies with observations have been described by a few authors (White,

1980; Hartman and Gahn, 1980; Charney

al.,

1981; Dole and Gordon,

1983). All of these agreed that the observational evidence supporting the

theoretical models in their essential prediction- i.e., the existence

multi-

ple regimes

was sparse. In this article, we address the same question. We

find, contrary to these recent studies, that in the context of the data as here

considered, there is evidence that the large-scale dynamics of the atmosphere

are consistent with the presence ofmore than one regime (in some sense that

will be explained later). In one regime the planetary-scale waves have large

amplitude; in another the same waves do not show appreciable amplitude.

posteriori,

we find that events falling into the first group can be associated

with what from a synoptic and subjective point of view would resemble

major blocking episodes. This result does not contradict, when examined in

227

Copynght

1986

by Academic

Press,

Inc.

rights

reproduction

any

form

reserved.

ADVANCES

GEOPHYSICS,

VOLUME

228

ALFONSO

SUTERA

detail, the previously mentioned studies. When we consider the specific state

variables of those studies, we confirm the results of their authors. Hence, the

different conclusions we have reached have their source in our having con-

sidered different variables. In Section

we describe the process that has led

us to consider this particular set of variables rather than any other. The data

source and its processing are described in Section

In Section

we illustrate

the technique employed to calculate the probability density associated with

our random sample set. In Sections

through

we present our principal

results. Conclusions and some speculations drawn from them are offered in

Section

THEORETICAL

BACKGROUND

illustrate the ideas which guided our observational study, it is worth-

while to recall

few basic concepts about the theory of orographically in-

duced stationary waves in the atmosphere, within the framework of a simple

model that we borrow from Benzi

al.

(1986)

(see

also

Speranza, this

volume), and that we slightly modify for our present purposes. Let us con-

sider a barotropic atmosphere confined to a khannel and flowing over a

topography that will

here considered the only relevant inhomogeneity of

the earth's surface. The governing equation expresses the conservation of

potential vorticity. In this

case,

the potential vorticity,

is defined as

(fo/H)h

(1)

where

the streamfunction, the latitudinal derivative of the Coriolis

force,

the Coriolis parameter at

45"N

latitude,

the equivalent atmo-

spheric depth, and

the surface elevation. Hence the equation of motion is

(2)

we split the streamfunction into its zonal average

and the departure

we have

y,q)

dissipation

Y=W+4

(3)

Let us assume that

-Uy.

In this case the governing equation

Jtrb,

(foh/H)]

U(h/H)

d,h

=dissipation

(4)

VII

neglect in

Eq.

(4)

all

but the linear terms

111,

IV,

and

VII,

we get

a,A4

ax4

d-4

(US,/H)

a,h

dissipation

(5)

DENSITY DISTRIBUTION

ATMOSPHERIC

FLOW

229

Equation

(5)

reduces

the Charney

Eliassen model

949) when

&,,

is set

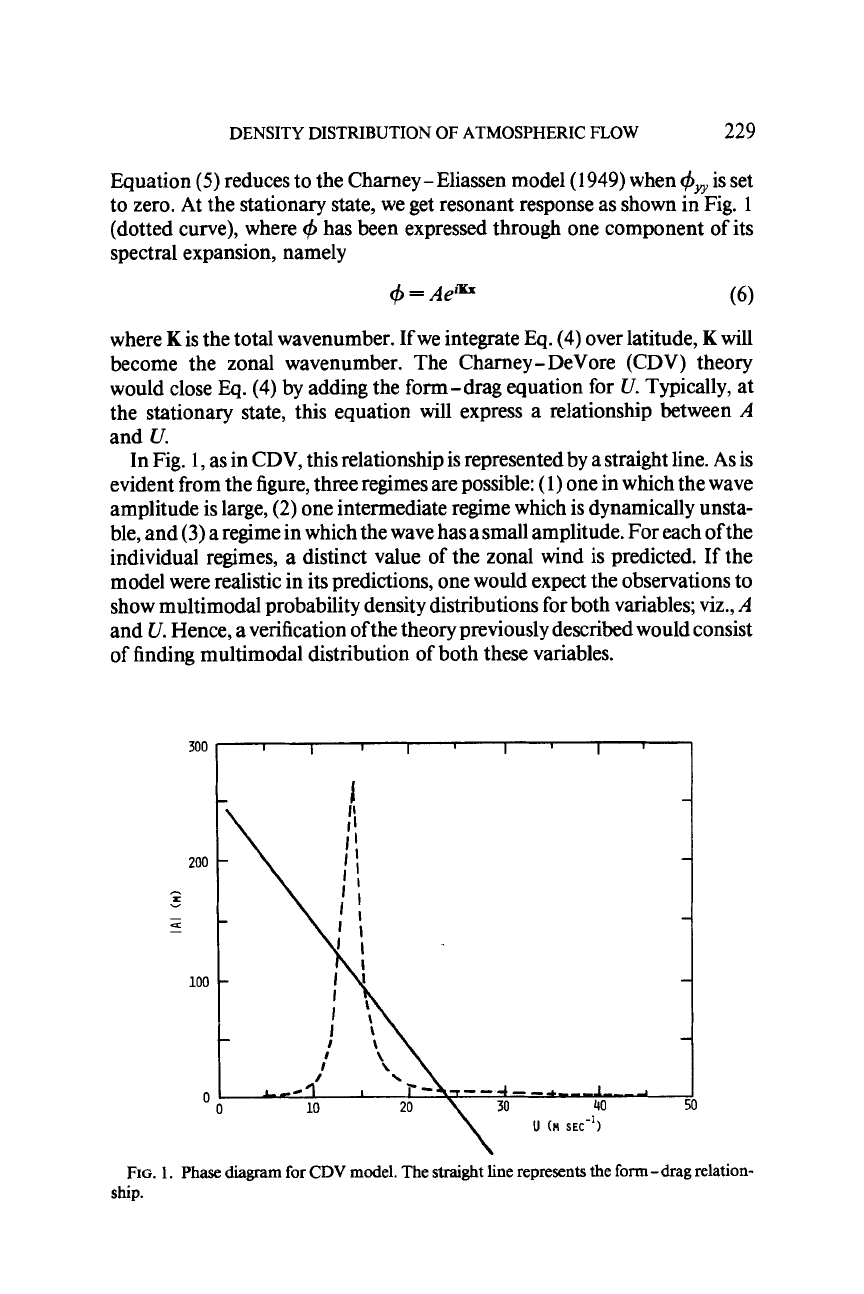
to zero. At the stationary state, we get resonant response as shown in Fig.

(dotted curve), where

has been expressed through one component

its

spectral expansion, namely

Ae*=

(6)

where

is the total wavenumber.

we integrate Eq.

(4)

over latitude,

will

become the zonal wavenumber. The Charney -DeVore (CDV) theory

would close

Eq.

(4)

by adding the form-drag equation for

Typically, at

the stationary state, this equation will express a relationship between

and U.

In Fig.

as in CDV, this relationship is represented by a straight line. As is

evident from the figure, three regimes are possible:

(1)

one in which the wave

amplitude is large, (2) one intermediate regime which is dynamically unsta-

ble, and

(3)

regime in which the wave has a small amplitude. For each

the

individual regimes, a distinct value

the zonal wind is predicted.

the

model were realistic in its predictions, one would expect the observations to

show multimodal probability density distributions for both variables;

viz.,

and

Hence, a verification of the theory previously described would consist

of finding multimodal distribution of both these variables.

300

200

100

FIG.

Phase diagram

for

CDV

model. The straight line represents the form-drag relation-

ship.

230

ALFONSO

SUTERA

THEDATA

The Charney-Eliassen equation, Eq.

(4),

has long been thought to be a

good representation of the

gross

features of the Northern Hemisphere's

midlatitude winter circulation; hence, we considered data including four

winters where winter is artificially defined as the period extending from

December through

February. Equation

(4)

has been often applied to the

500-mbar surface (Charney and DeVore,

1979).

we consider data at the

500-mbar level. Finally, since

Eq.

(4)

assumes geostrophic motion, the

streamfunction is properly represented by the geopotential gZ, where

gravity. Consequently, our analyses will be concerned with samples deduced

from the 500-mbar geopotential height. The data, originally archived in the

form

spherical harmonic coefficients, were retrieved and then interpo-

lated onto a regularly spaced latitude-longitude grid with a

5.625'

resolu-

tion in each direction. After the data were

prepared, the following prepro-

cessing was performed:

For each day an average over a latitude band (in our case a straight

algebraic mean) was calculated, obtaining a 64dimensional array. It was

then projected onto Fourier space by employing a standard fast Fourier

transform. Although the results described hereafter were deduced by latitude

averaging between

and

75"N,

we studied the effects of the width of the

latitude band on our results by considering other (narrower) latitudinal

bands. Besides obvious effects on the total amplitude of the waves, no other

significant differences were noticed.

For the same day, the mean zonal wind was evaluated geostrophically

from the geopotential height gradient in the latitudinal band considered

above. We noted that employing the classic Rossby (two-dimensional) for-

mula, the resonant stationary wavenumber oscillated between zonal wave-

numbers

2,3,

and

we decided to consider the variance associated with

the combined amplitude of these three wavenumbers for each day:

(C,ICJ~)'/~,

complex amplitude of wavenumber

i, i

At the completion ofthese operations, we were left with two samples of

size

1552:

the mean zonal wind

and the variance

the combined

amplitudes of wavenumbers

and

here designated

(n=

N).

For our purposes, we needed

further process the samples

that each

sample point could be considered to

statistically independent of all the

others. This is obviously not true for the

raw

dataset, since it is known that

atmospheric variables decorrelate over a finite time period.

In addition, our sample

sets

might contain other longer trends that could

not

directly connected with the natural variability of the system but owe

DENSITY DISTRIBUTION

ATMOSPHERIC

FLOW

their behavior to variations of the external forcing itself. Such trends might

be easily isolated on the lower end of the frequency spectrum and they would

correspond to well-known frequencies such as the annual cycle and its sub-

harmonics. To remove these trends we proceeded as follows.

For each variable set, we determined the autocorrelation function and

its Fourier transform.

From the observed decay ofthe autocorrelation function, we estimated

the decorrelation time. This turned out to be about

days for both variables.

This is in agreement with previous analyses (see, for example, Leith, 1978).

From the power spectrum, we noted a strong annual cycle and three

detectable subharmonics.

To eliminate the short-frequency variability, we designed a low-pass filter

with a cutoff frequency of

days. Then the data were resynthesized. To

eliminate the low-frequency variability, we detrended the data by using the

following method. For each day of the winter periods, we considered

{.>;=A

2r+

)i+j

(7)

where

(see Priestley, 1981). By employing this method we detrended

any variability longer than 90 days, and, hence, the year and its detectable

subharmonics.

done, we considered the five distinct datasets- the first

four, one for each

year,

contained

90 observations, while the last one

contained

360

observations, which were obtained by grouping together

the winters after the individual winter means were subtracted. The last step

was performed to avoid any residual long-term variability.

The two datasets

prepared allowed us to study

(1)

the probability den-

sity distribution induced by the data for each winter and

(2)

the probability

density distribution induced by all the data available.

NONPARAMETRIC PROBABILITY DENSITY

ESTIMATION

Since the general form of the probability density for our sample is un-

known, we must use the nonparametric estimation theory. Among nonpara-

metric estimators of unknown probability density associated with a random

sample, the oldest and most frequently used is the histogram.

histogram is

a maximum likelihood (ML) estimator in the sense that it maximizes the

likelihood function with good consistency properties (see, for example, Scott

al.,

1977).

disadvantage of such an estimation is that it becomes very

noisy when the mesh size tends to zero (number of bins tends to infinity), and

moreover does not tend in this case to the Dirac-delta at the sample point.

232

ALFONSO

SUTERA

Since, once we have deduced our estimate of the density, we would like to

perform some statistical evaluations of “the goodness

the fit,” this unde-

sirable property of the histogram turns out to be

major handicap.

different approach to density estimation, that has the same advantages

as the histogram but avoids its shortcomings, is the method of maximum

penalized likelihood (MPL) (see Scott

al.,

1977). This technique allows

combine maximization of both the likelihood function and a penalizing

smoothness function by taking explicitly into account the smoothness of the

density through a free parameter that we shall call

The MPL method consists in finding the maximum of the following score

functions:

with the constraint

Wdt

where

are the observations and Wis any density. The discrete approxima-

tion to Eq.

(1)

can

solved by employing an algorithm implemented and

incorporated into the International Mathematical Statistical Library

(IMSL), and in this article we used their routine NDMPLE on our data.

The external parameters to be provided to the algorithm (besides the data)

are

(1)

the mesh points at which the density must be evaluated and

(2)

the

hyperparameter

We decided to choose

mesh points when we evaluated

the density corresponding to the variable

while 15 mesh points were

employed for the variable

This choice was based by assuming an experi-

mental error in determining

and

m and

cm sec-’, respectively.

Once a probability density has been estimated,

already mentioned, it

will depend on the smoothness parameter

The choice ofa is arbitrary, and

not

deduced from the data (in other words, it is specified

priori).

However, for any

the corresponding theoretical probability density can

compared to the sample probability density through classical tests such as the

Kolmogorov

Smirnov

(K-

test. For the sake of clarity, we recall that the

K-S

test consists

evaluating the quantity:

SUP[S(xj)

P(X~

a)]

Sup

Supremum over all

(9)

where

and

are the sample probability density and the theoretical proba-

bility density, respectively, at the sample point

xi.

It is known that the

statistic

defined by Eq.

(9)

follows the

K-S

distribution and we can

DENSITY DISTRIBUTION

ATMOSPHERIC

FLOW

233

evaluatep,, i.e., the probability of an occurrence ofKthat is less than that of

a random variable with that distribution. It follows by this definition that as

p(xi,

takes on a greater resemblance to

we would have better confidence

Taken to the extreme, if

p(xi,

were found by the combination of as

many Dirac-deltas as there were data points, the fit, as defined by examining

would be perfect. Of course such a

would not be representative of the

true density because such a probability would predict that ifx, is an outcome,

then the next outcome will be

with probability

Now it is easy to show

that the

MPL

estimation tends to a Diracdelta at the sample points as

(the estimation optimizes the maximum likelihood), hence a

K-

test alone

would help to distinguish between an oversmooth

and one closer to the

data. But, on the contrary, the estimation would be insufficient to bound

from below the optimal

For this reason, we decided to calculate different

densities by decreasing the value of the hyperparameter

up to the point on

which the confidence level given by the

K-

test would reach the value

95%.

RESULTS

In this section we will show our main results on the nature of the density

distribution of the data described in Section

We first start by considering each individual winter period in the set

the

values of the amplitude

We recall that, for this variable, we used

mesh

points in evaluating the density in accordance with the previously discussed

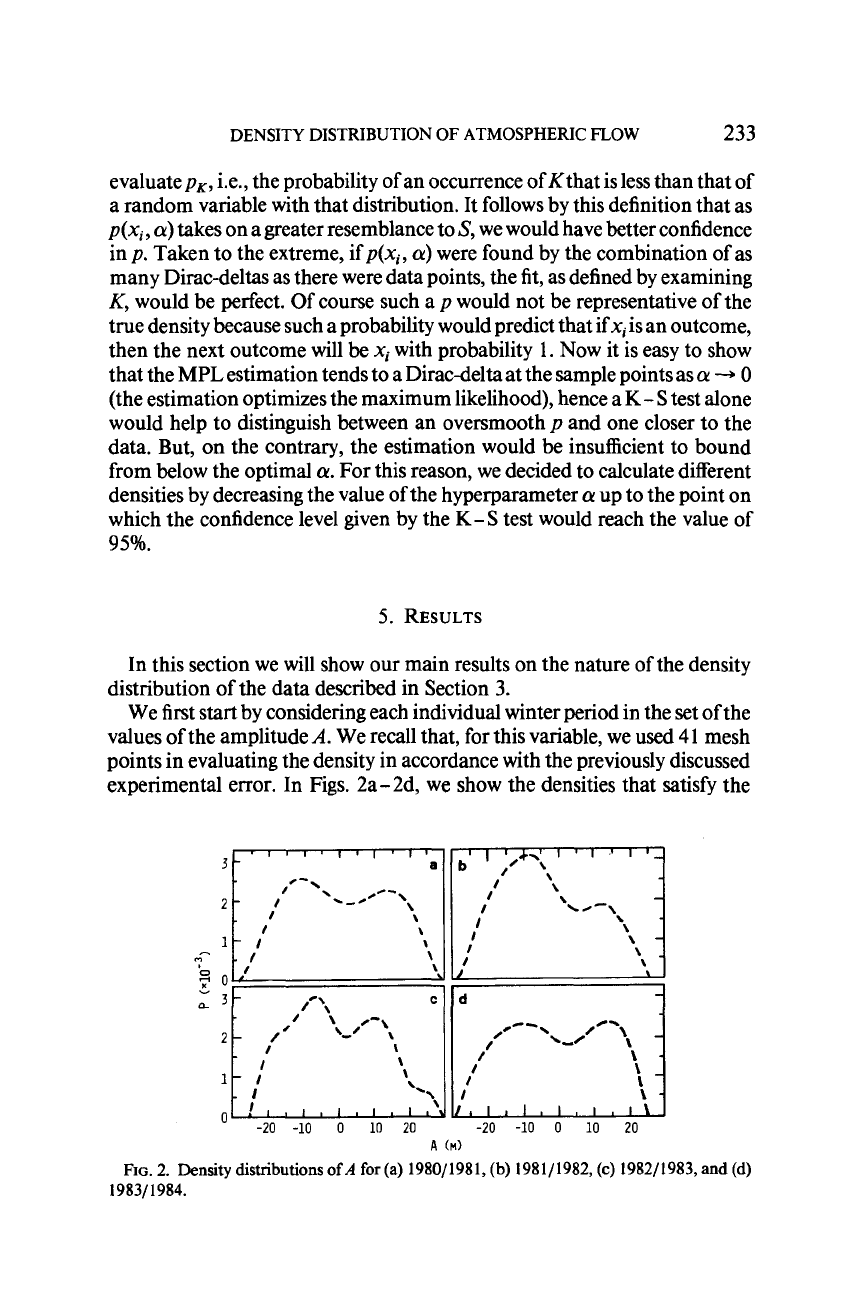
experimental error. In Figs. 2a-2d, we show the densities that satisfy the

1p;

,'\>

-20

-10

*\.-,

(MI

FIG.

2. Density distributions

ofA

for

(a)

1980/1981, (b) 1981/1982,

(c)

1982/1983,

and (d)

1983/1984.