Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

230 8

Atmospheric

Radiation

1.00

~ :! I / i!

...... z=H

0.0 0.45 0.5 0.55 0.6

WAVELENGTH (pm)

Figure 8.18 Absorptivity contributed by an individual absorption line at 0.5 tzm for an ab-

sorber with a uniform mixing ratio and for the layer extending from the top of the atmosphere

to a height z of 5 scale heights, 3 scale heights, and 1 scale height. As the layer extends down-

ward, where absorber concentration increases exponentially, the line becomes saturated, first at

its center but eventually over a widening range of wavelength.

may be represented in terms of the Lorentz profile (8.31.1). As ~-~ increases,

so does a~ (Fig. 8.18). Eventually, the absorptivity reaches unity near the line

center, at which point the corresponding frequencies are fully absorbed. The

line is then said to be

saturated,

which corresponds to the limit of

strong

absorption.

Subsequent absorption can occur only in the wings of the line, which are

pushed out by the ever-widening region where the line is saturated. In a

band containing many lines, saturation leads to the absorption spectrum fill-

ing in between discrete features. This occurs first for the narrowly separated

vibration-rotation transitions (e.g., Figs. 8.11, and 8.13). Over sufficient opti-

cal depth, those clusters merge to produce continuous bands of absorption,

such as those appearing in Figs. 8.1 and 8.9. The strong absorption limit ap-

plies to bands that dominate vertical energy transfer in the atmosphere. It

is the basis for a powerful approximation that reduces the three-dimensional

description of diffuse LW radiation to a one-dimensional description.

8.4.2 Two-Stream Approximation

Embodied in the flux transmission function (8.50) is an integral over zenith

angle, which collects contributions from diffuse radiation, and another integral

over frequency. Because E3(rv) depends on frequency, the two integrations are

related. In the strong absorption limit, the integral over zenith angle can be

approximated fairly accurately by incorporating the spectral character of ~.

8.4

Radiative Transfer in a Plane Parallel Atmosphere

231

where

Integrals on the right-hand sides of (8.51) involve the term

d~ (Az~)d~-'~ -- 2 fa

d/,,,

Ez(Ar")Pk"dz'

A----v ' (8.52.1)

a~ -I,; - ~1. (8.52.2)

If the band described by ~ is saturated, the factors k~ and E2(A~'v) have recip-

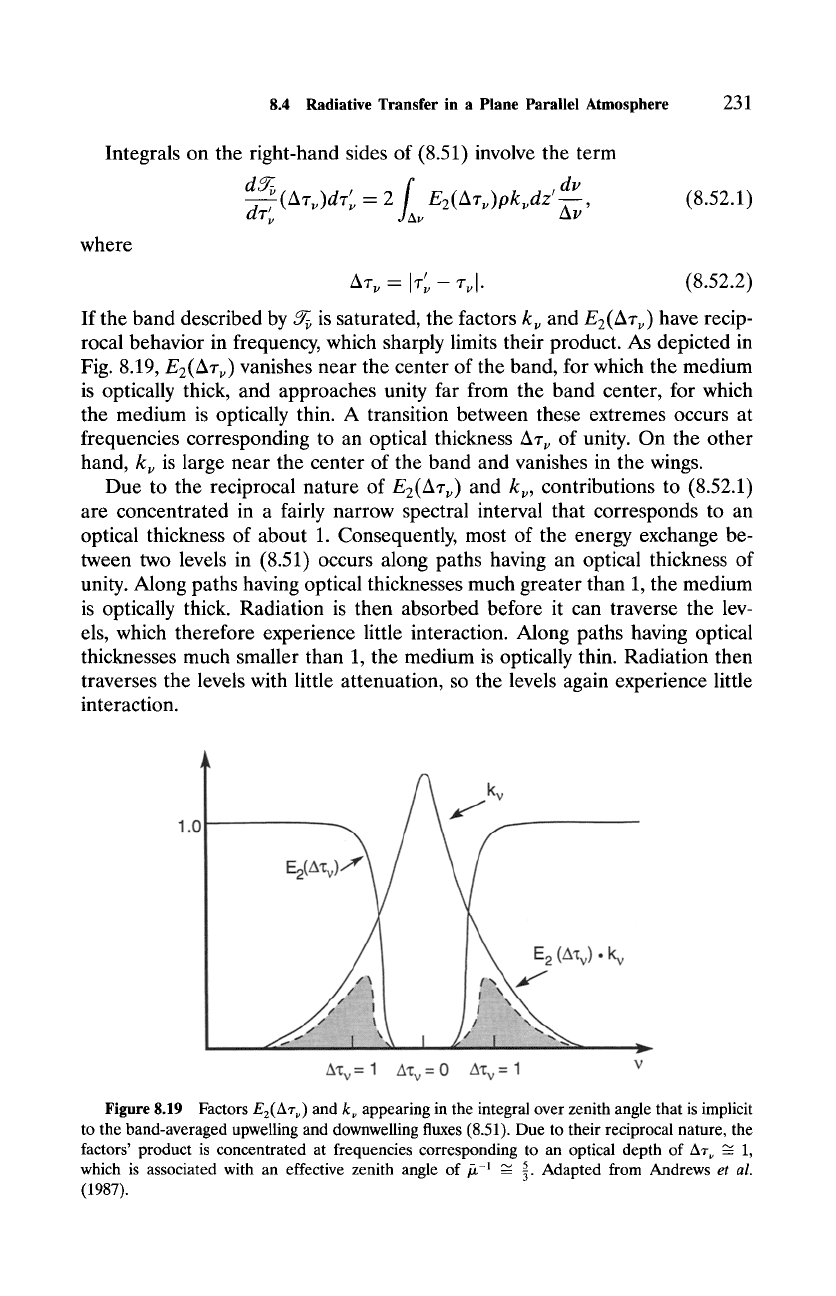
rocal behavior in frequency, which sharply limits their product. As depicted in

Fig. 8.19, E2(Az~) vanishes near the center of the band, for which the medium

is optically thick, and approaches unity far from the band center, for which

the medium is optically thin. A transition between these extremes occurs at

frequencies corresponding to an optical thickness A~'~ of unity. On the other

hand, k~ is large near the center of the band and vanishes in the wings.

Due to the reciprocal nature of E2(Az~) and k~, contributions to (8.52.1)

are concentrated in a fairly narrow spectral interval that corresponds to an

optical thickness of about 1. Consequently, most of the energy exchange be-

tween two levels in (8.51) occurs along paths having an optical thickness of

unity. Along paths having optical thicknesses much greater than 1, the medium

is optically thick. Radiation is then absorbed before it can traverse the lev-

els, which therefore experience little interaction. Along paths having optical

thicknesses much smaller than 1, the medium is optically thin. Radiation then

traverses the levels with little attenuation, so the levels again experience little

interaction.

1.0

,~ kv

E2(A%

).k~

AI: v=l A%=0 A%=1 v

Figure

8.19 Factors EE(AZ~) and k~ appearing in the integral over zenith angle that is implicit

to the band-averaged upwelling and downwelling fluxes (8.51). Due to their reciprocal nature, the

factors' product is concentrated at frequencies corresponding to an optical depth of A~- ~ 1,

5 Adapted from Andrews

et al.

which is associated with an effective zenith angle of

f/-1 ~ 3"

(1987).

232 8

Atmospheric Radiation

For any specified A r~, an effective inclination /2 may be found such that

the exponential integral over zenith angle is given by

2E3(Ar~) = exp ----~- . (8.53.1)

Because contributions to (8.51) are restricted to Ar~ ~ 1, the parameter/2-1,

which is referred to as the

diffusivity factor,

is likewise restricted to a narrow

range of values. For A%, = 1, the diffusivity factor assumes the value

/2_ 1 _~ 5 (8.53.2)

The implication of this analysis is that the zenith angle dependence in (8.51)

can be eliminated in favor of an effective inclination/2, which reduces the

multidimensional description to integrals over optical depth alone. Diffuse

transmission which is embodied in ~(~'~) is then equivalent to that of a colli-

mated beam inclined at a zenith angle of 53 ~

~(r~) = ~(r~,/2) (8.53.3)

or, alternatively, inclined at zero zenith angle but through an optical thickness

expanded by a factor of 3"

Known as the

exponential kernel approximation,

this simplification follows

from the fact that radiative exchange in strong bands is dominated by spectral

intervals in which A~- = 1. For this reason, most of the LW radiation emitted

by the earth's surface is captured in the lower troposphere, which is made

optically thick by strong absorption bands of water vapor and carbon dioxide.

Likewise, incident SW radiation in particular wavelengths of UV is absorbed

in the stratosphere over a limited range of altitude (Fig. 8.3), which is made

optically thick by photodissociation at those wavelengths. 2 The development

leading to (8.53) is one of several so-called

two-stream approximations

that

eliminate the zenith angle dependence in Ft and F+. Applicable under fairly

wide circumstances (e.g., in the presence of scattering), this formalism leads

to diffusivity factors in the range 23- < t2 -1 < 2, depending on the particular

approximation adopted.

Because/x enters the equations jointly with ~-~, the full description of ra-

diative transfer in a plane parallel atmosphere can be reduced to a vertical

description by taking/x = -t-/2 for upwelling and downwelling radiation and

introducing the transformation

9 ._ /~-1

'/'A 7"A

F~*(T]) = 7rlA(T ~, -+-/2),

(8.54.1)

(8.54.2)

(8.54.3)

2For weak bands that are unsaturated near their centers, energy exchange may arrive from

smaller values of At., which correspond to larger values of/2 -1.

8.5 Thermal Equilibrium

233

which relies on hemispheric isotropy. Then integrating the radiative transfer

equation (8.37) over upward and downward half-spaces yields for the budgets

of upwelling and downwelling radiation

dF~ = F~ - J'A,

(8.55.1)

dr]

dF~ _ F~ - J*~.

(8.55.2)

dr~

The foregoing development applies to LW radiation, which is inherently dif-

fuse. SW radiation, which is parallel beam in the absence of scattering, involves

only a single direction/z.

8.5 Thermal Equilibrium

8.5.1 Radiative Equilibrium in a Gray Atmosphere

We are now in a position to evaluate the thermal structure toward which radia-

tive transfer drives an atmosphere. To do so, we consider a simple model of the

earth's atmosphere: a

gray atmosphere

that is transparent to SW radiation but

absorbs LW radiation with a constant absorption cross section which is inde-

pendent of wavelength, temperature, and pressure. Consider a plane parallel

gray atmosphere that is nonscattering, motionless, and in thermal equilibrium

with incoming SW radiation and with a black underlying surface. Individual

layers of the atmosphere then interact only through LW radiation.

For an incremental slab of thickness

dz,

the first law (2.22.2) implies

dT dp

pCp

dt dt = P{I

= dz'

(8.56.1)

where

F = F t - F + (8.56.2)

is the net LW flux integrated over wavelength and ~r is the local rate at which

heat is absorbed per unit mass or the

specific heating rate.

The convergence of

LW flux on the right-hand side of (8.56.1) represents the local radiative heating

rate per unit volume, which forces the atmosphere's thermal structure. In

equilibrium, the left-hand side vanishes. Then the net flux must be independent

of height

F = const, (8.57)

which implies that radiative energy does not accumulate within individual

layers.

234 8 Atmospheric Radiation

The upwelling and downwelling components of F are governed by (8.55).

Adding and subtracting yields the equivalent system

where

dr*

= F - 2B*, (8.58.1)

= F, (8.58.2)

d'r*

P - F 1' + F ~ (8.58.3)

represents the total flux emanating from an incremental slab and all quantities

have been integrated over wavelength. With (8.57), (8.58.2) gives

and (8.58.1) reduces to

Thus, the emission

F - F'r* + c

(8.59.1)

F- 2B*. (8.59.2)

B*(z*) = z~z* + B~

(8.60)

increases linearly with optical depth from its value B~ at the top of the atmo-

sphere (Fig. 8.20).

For thermal equilibrium of the atmosphere and surface collectively, the

incident SW flux

F 0 = (1 - d)Fs (8.61)

(See. 1.4.1) must be balanced by the outgoing LW flux at the top of the

atmosphere

Ft(0) - F 0. (8.62)

Because the downwelling LW flux at the top of the atmosphere vanishes, F(0)

and F(0) each reduce to FI"(0), so by (8.57)

F = F0. (8.63)

The net LW flux at any level equals the SW flux at the top of the atmosphere.

Then incorporating (8.59.2) yields

B*('r*) -F0 ('r* + 1), (8.64)

which is shown in Fig. 8.20 alongwith U and F +. Under radiative equilibrium,

the upwelling and downwelling fluxes differ by a constant, so the net heating

at any level vanishes.

Consider next thermal equilibrium of the surface. Since it is black, the

surface absorbs the incident SW flux in addition to the downwelling LW flux

8.5 Thermal Equilibrium

235

RADIATIVE EQUILIBRIUM

I;* =0

\ \\

\ \ F:(~*)

\ \, F+(~*)

\ \\

\ \ B*('~*)

\ \\B*

\ \\

\ ,,

\ \\

\ ',

F $ \ \ \ F I"

\ \\

\ \

\ \\

\~ F

\ \

F'I'(I:,~) B*('~*s) \\ \\_ _ XB*('t'*s)

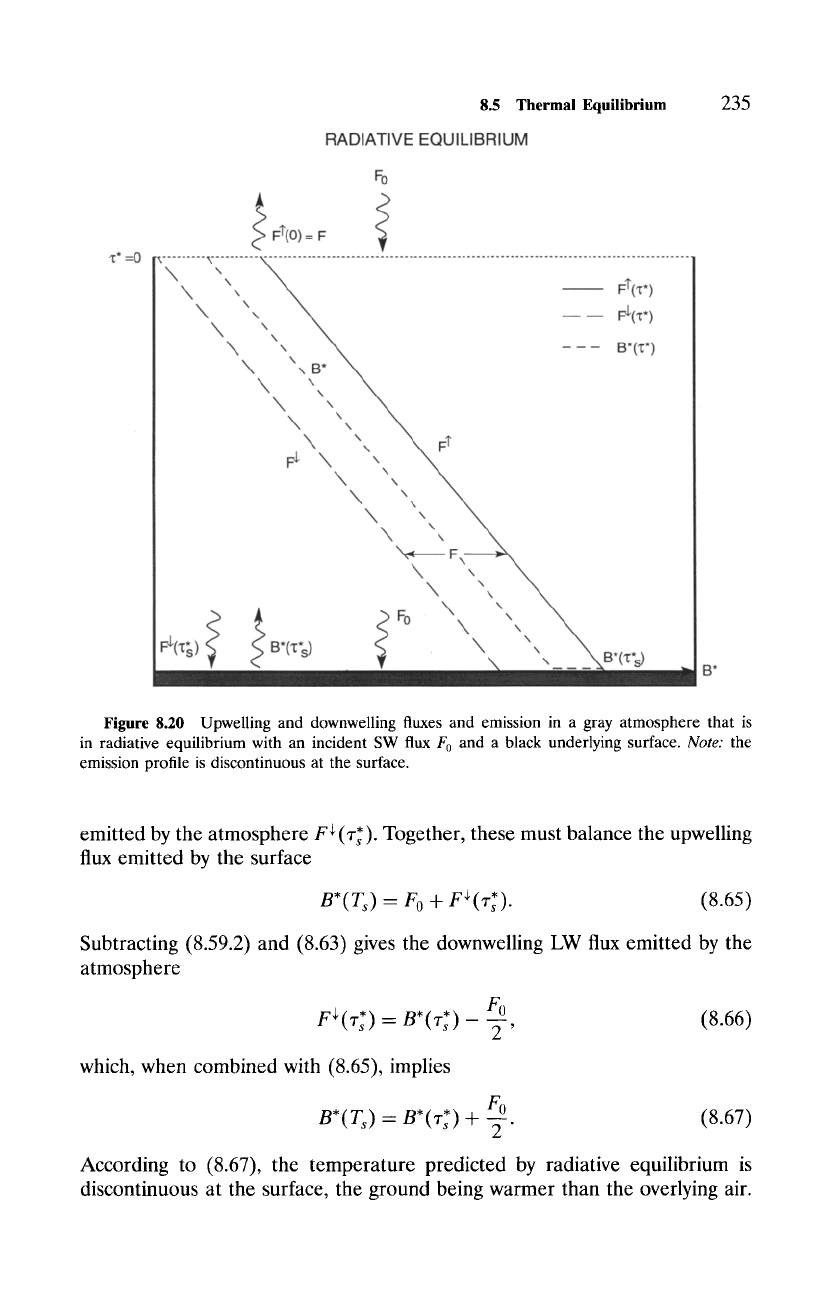
Figure 8.20 Upwelling and downwelling fluxes and emission in a gray atmosphere that is

in radiative equilibrium with an incident SW flux F0 and a black underlying surface.

Note:

the

emission profile is discontinuous at the surface.

emitted by the atmosphere F+ (~-]'). Together, these must balance the upwelling

flux emitted by the surface

B*(Ts) - F o + F+('r'~).

(8.65)

Subtracting (8.59.2) and (8.63) gives the downwelling LW flux emitted by the

atmosphere

F~ (8.66)

F ~" ('r~ ) - B* ('r~ ) 2'

which, when combined with (8.65), implies

B*(T~) - B*(~-s) + -~-. (8.67)

According to (8.67), the temperature predicted by radiative equilibrium is

discontinuous at the surface, the ground being warmer than the overlying air.

236 s Atmospheric

Radiation

The emission profile (8.64) determines the radiative equilibrium tempera-

ture through

B*('r*) = "n'B[T("r*)]

= o'T 4. (8.68)

Because the atmosphere is hydrostatic, density decreases with height approx-

imately exponentially (1.17) and by (8.36) so does z*. Further, most of the

atmosphere's opacity follows from water vapor and clouds (Fig. 8.1), which

are concentrated in the lowest levels. Therefore, the linear variation with op-

tical depth of B* translates into a steep decrease with height of temperature.

At the surface, the lapse rate is infinite because the radiative equilibrium tem-

perature is discontinuous there.

Taking the optical depth to vary with height exponentially

~" = Zse-~,

(8.69)

where h = 2 km is symbolic of the absolute concentration of water vapor (Fig.

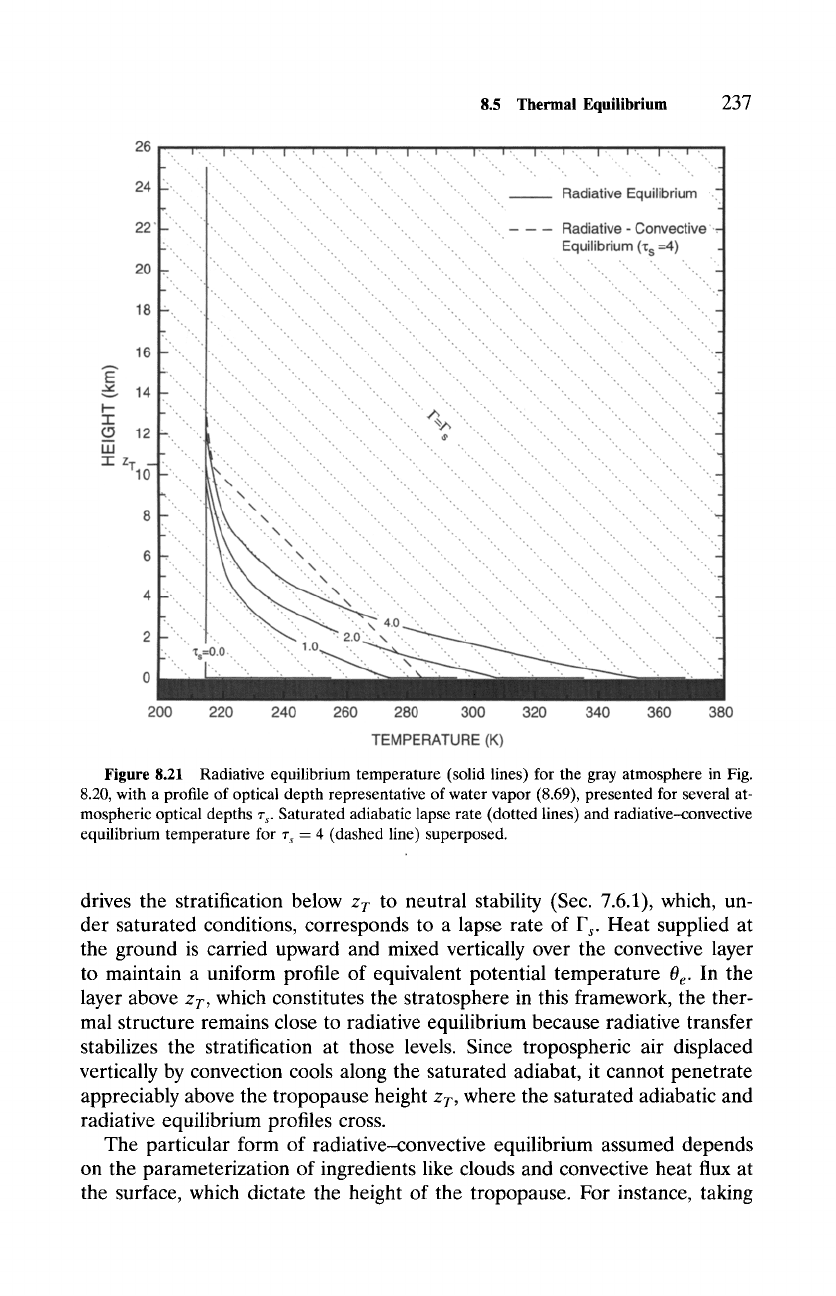
1.14), and F 0 = 240 W m -2 results in the temperature profiles (solid lines)

shown in Fig. 8.21. For given z~ > 0, the surface temperature exceeds that in

the absence of an atmosphere (z~ = 0) and increases with the atmosphere's

optical depth. These features are manifestations of the greenhouse effect.

Radiative equilibrium temperature is maximum at the ground, where it varies

sharply with height and jumps discontinuously to the surface temperature Ts.

As z ~ oo, the radiative equilibrium temperature approaches a finite limiting

value "--'(~)4 ~ 215 K, which is called the

skin

temperature.

In a neighborhood of the surface, temperature decreases with height more

\ z

rapidly than the saturated adiabatic lapse rate F s "~ 6.5 K km -1 (dotted lines),

which characterizes moist neutral stability. Thus, each of the radiative equilib-

rium temperature profiles in Fig. 8.21 is hydrostatically unstable in its lowest

levels. For an optical depth of z~ = 4, the radiative equilibrium profile is con-

ditionally unstable below 6 km, absolutely unstable below about 5 km, and has

a lapse rate of some 36 K km -1 at the ground.

8.5.2 Radiative-Convective Equilibrium

If air motion is accounted for, convection develops spontaneously to neutral-

ize the unstable stratification introduced by radiative transfer. The

radiative-

convective equilibrium

that ensues, which is superposed in Fig. 8.21 for z~ = 4

(dashed line), produces two layers of distinctly different character. In the layer

below a height

zr,

which constitutes the troposphere in this framework, ther-

mal structure is controlled by convective overturning that is driven by radiative

heating and its continual destabilization of the stratification. Since it operates

on a timescale much shorter than radiative transfer, convective overturning

8.5 Thermal Equilibrium

237

I--

"1-

(.9 12

L.M

-1-

ZT1 O-

.. I..

.. ...

"..

%9 ".

- "...

"..

-~.

9149

"..

".,, .,

I'. ". I. I .. I'. t .. I ". I .

-. .. -.

"-9149 9 9 .9 9 9

""'... . ' . '. .

9 . . .. . .. .

9 ... . 9 . .

.9 .9 9 9 9

'"9 . . .9 . .. 9149149

-. ... . ". . .

9

- .9 9149 9149 . .. 9 9

9 9 . . 9 9149

",,.

9 . .. . . .

....

". .. . . .. .

9 .. . .

9

".. . .. .

9 . .. 9 .

"9149 I.. I'. I. I. I'.. I ". I ..

.. .. . -.

.. . . ..

". .. .. . 9

.. 9 9 ,.9 9 .

Radiative Equilibrium ,-

Radiative - Convective 9

Equilibrium ('t s =4)

.. .

9 .. .

9 . ...

".. -... ...

'.. . . .. .

__ ,,.

.,,

' ,

'-,,,

,. , 9 ,, ,. , .

9 ,, 9 ,, ,, 9 9 9

",. \ "., , ,..

\ -,, .,,

\ - ",.

,9 ,, ., ., ,

",~" 4.0 "9 "9149 9 9149 " ",,'"'9

1.09 \ "'.. 9 "., ... "-, .,

2}. 9149 I 9149149 9149 ,~9

t'" ~s=~176 "

" "

dO q

9

o=~

"'-. . ". --

.. ..-

-. "...-

"'...

9 9 .. ..

200 220 240 260 280 300 320 340 360 380

TEMPERATURE (K)

Figure 8.21 Radiative equilibrium temperature (solid lines) for the gray atmosphere in

Fig.

8.20, with a

profile of optical depth representative of water vapor (8.69), presented for several at-

mospheric optical depths T s. Saturated adiabatic lapse rate (dotted lines) and radiative-convective

equilibrium temperature for

~'s = 4

(dashed line) superposed.

drives the stratification below

z T

to neutral stability (Sec. 7.6.1), which, un-

der saturated conditions, corresponds to a lapse rate of F s. Heat supplied at

the ground is carried upward and mixed vertically over the convective layer

to maintain a uniform profile of equivalent potential temperature 0e. In the

layer above zT~, which constitutes the stratosphere in this framework, the ther-

mal structure remains close to radiative equilibrium because radiative transfer

stabilizes the stratification at those levels. Since tropospheric air displaced

vertically by convection cools along the saturated adiabat, it cannot penetrate

appreciably above the tropopause height

ZT,

where the saturated adiabatic and

radiative equilibrium profiles cross.

The particular form of radiative-convective equilibrium assumed depends

on the parameterization of ingredients like clouds and convective heat flux at

the surface, which dictate the height of the tropopause. For instance, taking

238 8

Atmospheric

Radiation

the height of the convective layer equal to the maximum height of instability

under radiative equilibrium predicts one tropopause height. On the other

hand, taking the air temperature at z -- 0 equal to the surface temperature

under radiative equilibrium leads to a different tropopause height.

An alternative that circumvents ambiguities surrounding convection and is

consistent with the radiative framework behind (8.64) requires the convec-

tive layer to supply the same upward radiation flux at the tropopause as that

under radiative equilibrium (Goody and Yung, 1989). Tantamount to presum-

ing the stratosphere is unaffected by vertical motions below, this formalism

provides a self-consistent (albeit limited) rationale for determining radiative-

convective equilibrium. Integrating (8.55) as before leads to expressions valid

under arbitrary conditions for the upward and downward radiation fluxes

F~(r *) = B(Ts)exp('r* - "r~)* _ l""j~.,"

fo'"

- exp( ' -

exp(r* -

z')B*[T(r')ldr'

(8.70.1)

(8.70.2)

where convection has been presumed efficient enough to maintain the surface

at the same temperature as the overlying air. Then equating (8.70.1) to the

upward flux under radiative equilibrium

Ft(r *)

= -~-(r* + 2), (8.71)

which follows in the same manner as (8.66), obtains a surface temperature

of T s ~ 285 K for Zs = 4. Superposed in Fig. 8.21, the radiative--convective

equilibrium temperature that follows (dashed line) is cooler in the lower tro-

posphere and warmer in the upper troposphere than the radiative equilibrium

profile and has a tropopause at about 10.5 km, in qualitative agreement with

observed thermal structure. For a characteristic extinction scale of h = 2 km,

lies several optical depths above the ground, so the stratosphere is close to

the atmosphere's skin temperature.

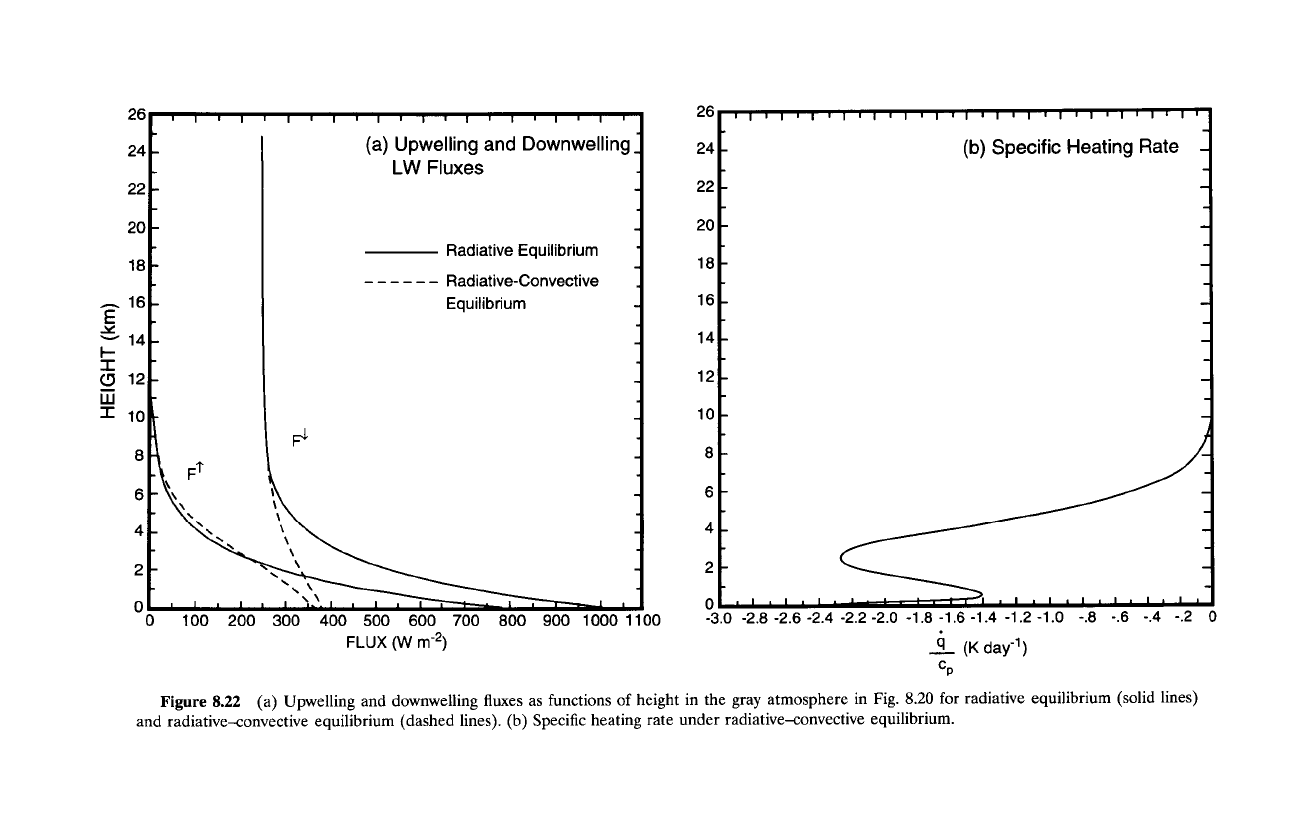
The corresponding upward and downward fluxes (dashed lines) are shown

as functions of height in Fig. 8.22a along with those under radiative equi-

librium (solid lines). Reduced temperature in the lower troposphere leads to

smaller upward and downward fluxes that merge with the radiative equilibrium

profiles above Zr. To satisfy overall equilibrium, F~ approaches 0 and F 1" ap-

proaches 240 W m -2 as z ~ c~. Whereas the radiative equilibrium fluxes

preserve a constant difference, the net flux under radiative-convective equi-

librium varies with altitude below

ZT,

which implies nonzero radiative heating

in the troposphere. The specific heating rate

it/Cp

(Fig. 8.22b), which has

dimensions of degrees per day, is negative throughout the troposphere and

(u.l>l) J..H~DI=IH

(a) Upwelling and Downwelling

Fluxes

Radiative Equilibrium

------

Radiat ive-Convective

Equilibrium

100

200

300

400

500

600

700

800

900

1000 1100

FLUX

m-*)

I I

18 18

(b)

Specific Heating Rate

Figure 8.22

(a) Upwelling and downwelling fluxes as functions of height in the gray atmosphere in Fig.

8.20

for radiative equilibrium (solid lines)

and radiative-convective equilibrium (dashed lines). (b) Specific heating rate under radiativexonvective equilibrium.