Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

250 8

Atmospheric

Radiation

oxidation. These and other processes controlling optically active species are

temperature dependent, which introduces the possibility of feedback between

the two sides of (8.81).

Noteworthy is the mechanism controlling water vapor, which is the pri-

mary absorber in the IR. Temperature dependence in the Clausius-Clapeyron

relation (4.38) makes the water vapor abundance vary sharply with Ts. The

exponential dependence of saturation vapor pressure implies that an increase

of Ts can sharply increase the water vapor content of the atmosphere. En-

hanced cloud cover, which is likewise implied, further increases z~. By (8.81),

the increased optical depth results in a higher equilibrium surface tempera-

ture, which, in turn, increases the saturation vapor pressure and H20 content

of the atmosphere, and so forth.

Positive feedbacks like the one between temperature and water vapor sup-

port potentially large changes of

and other properties that characterize

climate. A paradigm of such changes is the so-called "runaway greenhouse ef-

fect," which is used to explain the present state of the Venusian atmosphere.

The evolution of a planet's atmosphere is thought to occur through slow dis-

charge of gases from the planet's surface. Atmospheric uptake of those gases

is limited by their saturation vapor pressures, which depend only on tempera-

ture (e.g., on T~). Because those gases are responsible for atmospheric opacity,

their saturation vapor pressures translate into the optical depth

"r s.

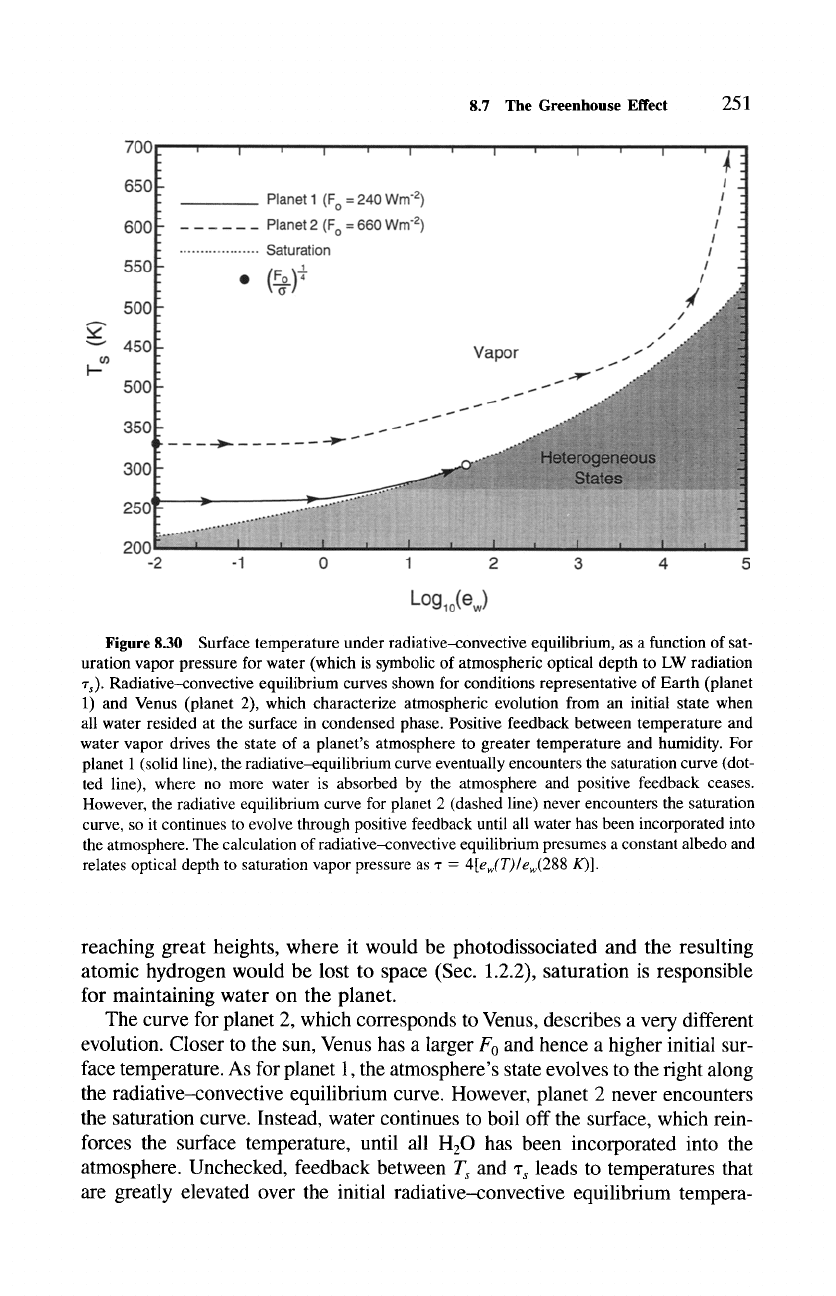
Plotting

T~ against log(ew), which is symbolic of

log('rs),

produces the saturation curve

(dotted line) in Fig. 8.30 separating heterogeneous states of water from vapor

phase alone.

The optical depth z~ and incident solar flux F 0 determine the surface tem-

perature of the planet, for example, via (8.81) under radiative equilibrium

or its counterpart (8.70) under radiative--convective equilibrium. Then the

surface temperature T~ defines a family of radiative-convective equilibrium

curves, two of which are superposed in Fig. 8.30. The curve for a particular

F 0 can be thought to represent the evolution of a given planet. For small

'r s,

T~ _~ (Fo/o')~,

which reflects the initial state of the planet when all of its water

resided at the surface in condensed phase. The situation for Earth is repre-

sented in the curve for planet 1 (solid line). Initially unsaturated, the atmo-

sphere incorporates water vapor from the surface, with concomitant increases

of its opacity ~'~ and surface temperature T~. Positive feedback between tem-

perature and water vapor then drives the state of the atmosphere to the right

along its radiative--convective equilibrium curve. Eventually, the atmosphere's

state encounters the saturation curve, beyond which further increases of

"r s

and

are prevented. For the conditions of planet 1, saturation is achieved at

a surface temperature of about 287 K. Subsequent increases of water vapor

are offset by condensation, which returns H20 to the planet's surface. Those

conditions describe a saturated system that contains multiple phases of water,

reflecting the present state of Earth's atmosphere. By preventing H20 from

8.7 The Greenhouse Effect

251

7001:

650~-- _ _ Planet 1 (F o =

Wm -2)

240

600~1" Planet 2 (F o = 660 Wm "2)

Saturation

5001-

,,r

450

I---

500

3501z-

....-- ---"

I ' I ~ I

Vapor ~ ~ "

00 :~.~,e..-:#~:rr.-.~ ~,, ..... ...,..~.~r .,.....e..~:.~ ~:~:~:~ ~. ~:~ , :,.~- ~:~ {~..-... ~:,,:..'.%..:..t~s~.-.~..~ :~.,~&,..~..#~..,:gv .~,---.;~:~.~- ~ ~.~:;r ~. - 9 %,~.~ ri,~i.;..T:~-:: :{. * ::~.~-~t~,..~:.~$,.,:#~:z~':~,~ ~ :. . ~ .: ~,,. ~r .

-2 -1 0 1 2 3 4 5

Log,o(e~)

Figure 8.30 Surface temperature under radiative-convective equilibrium, as a function of sat-

uration vapor pressure for water (which is symbolic of atmospheric optical depth to LW radiation

~'s)- Radiative-convective equilibrium curves shown for conditions representative of Earth (planet

1) and Venus (planet 2), which characterize atmospheric evolution from an initial state when

all water resided at the surface in condensed phase. Positive feedback between temperature and

water vapor drives the state of a planet's atmosphere to greater temperature and humidity. For

planet 1 (solid line), the radiative-equilibrium curve eventually encounters the saturation curve (dot-

ted line), where no more water is absorbed by the atmosphere and positive feedback ceases.

However, the radiative equilibrium curve for planet 2 (dashed line) never encounters the saturation

curve, so it continues to evolve through positive feedback until all water has been incorporated into

the atmosphere. The calculation of radiative-convective equilibrium presumes a constant albedo and

relates optical depth to saturation vapor pressure as -r =

4[ew(T)/ew(288 K)].

reaching great heights, where it would be photodissociated and the resulting

atomic hydrogen would be lost to space (Sec. 1.2.2), saturation is responsible

for maintaining water on the planet.

The curve for planet 2, which corresponds to Venus, describes a very different

evolution. Closer to the sun, Venus has a larger F0 and hence a higher initial sur-

face temperature. As for planet 1, the atmosphere's state evolves to the right along

the radiative-convective equilibrium curve. However, planet 2 never encounters

the saturation curve. Instead, water continues to boil off the surface, which rein-

forces the surface temperature, until all H20 has been incorporated into the

atmosphere. Unchecked, feedback between

and % leads to temperatures that

are greatly elevated over the initial radiative-convective equilibrium tempera-

252 s Atmospheric Radiation

ture. This is symbolic of the 750 K mean surface temperature of Venusmwhich

is some 400 K warmer than would result in the absence of its atmosphere.

Atmospheric composition suggested by the evolution of planet 2 also differs

fundamentally from that of planet 1. For initial water abundance comparable

to that of Earth, the Venusian atmosphere would reach a state in which H20

is its primary constituent. Water vapor would then be vulnerable to photodis-

sociation by UV, allowing atomic hydrogen to escape to space and free oxygen

to recombine at the surface through oxidation processes. In this fashion, atmo-

spheric water vapor would be systematically depleted and replaced by carbon

dioxide, which is consistent with the predominance of CO2 in the present-day

Venusian atmosphere.

For Earth, gases other than water vapor also contribute to the greenhouse

effect. Absorption by carbon dioxide is situated near the maximum of the LW

emission spectrum (Fig. 8.5). In tandem with the steadily increasing concen-

tration of CO2 (Fig. 1.11), this feature suggests that increased surface tem-

peratures are inevitable if the present trend continues. CFCs, methane, and

nitrous oxide follow carbon dioxide in importance. All have anthropogenic

sources that have been associated with increasing concentrations.

Were the preceding feedback to operate in isolation, small changes of tem-

perature (e.g., stimulated by occasional volcanic eruptions or anthropogenic

activities) could result in large shifts of the Earth's climate. In fact, the

temperaturemwater vapor feedback is but one of several believed to shape

climate. The involvement of properties like surface reflectivity (e.g., snow and

ice cover), clouds, and the distributions of optically active species is strongly

suggested by models of radiative-convective equilibrium, which exhibit marked

sensitivity to how such ingredients are prescribed. Clouds and aerosol, which

are treated in the next chapter, are especially important because they sharply

alter the absorption and scattering characteristics of the atmosphere.

Suggested Reading

An Introduction to Atmospheric Radiation (1980) by Liou is a very readable

treatment of radiative transfer. It includes discussions of solar variability and

band models.

Fundamentals of Modern Physics (1967) by Eisberg provides an excellent

overview of Planck's theory and the emergence of modem physics. It includes

a basic treatment of line broadening.

Aeronomy of the Middle Atmosphere (1986) by Brasseur and Solomon and Mid-

dle Atmosphere Dynamics (1987) by Andrews et al. contain excellent treatments

of radiative transfer in the stratosphere and mesosphere. They also include de-

scriptions of solar variability and its implications to UV radiation.

An advanced treatment of radiative transfer can be found in Atmospheric Ra-

diation (1989) by Goody and Yung, which contains an enlightening comparison

of two-stream approximations.

Problems

253

Atmospheric Ozone: Assessment of Our Understanding of Processes Controlling

Its Present Distribution and Change

(WMO, 1986) includes a detailed overview

of solar variability based on satellite measurements.

Special Functions and Their Applications

(1972) by N. Lebedev contains a

proper development of the exponential integral.

Hartmann (1994) provides an excellent overview of the earth's energy budget,

including a treatment of horizontal energy transport by the general circulation.

Ramanathan

et al.

(1989) provides an overview of recent satellite measure-

ments of the earth's radiation budget and observations of the solar constant.

Manabe and Strickler (1964) is a classic calculation of radiative-convective

equilibrium, which contains an estimate of thermal damping time inside the

troposphere.

Climate Change: The IPCC Scientific Assessment

(Houghton

et al.,

1990) con-

tains an overview of climate feedback mechanisms and assessments of how

well they are understood.

Problems

8.1. Calculate the brightness temperature of the earth based on (a) an ob-

served broadband OLR of 235 W m -2, (b) the outgoing narrowband flux

(Fig. 8.5) at A = 11 pm, (c) the outgoing narrowband flux at A = 9.6/zm,

and (d) the outgoing narrowband flux at A = 15 pm.

8.2. Derive the Stefan-Boltzmann law (8.15).

8.3. As the sun cools, its spectrum will shift toward longer wavelengths. Esti-

mate the change in the earth's equivalent blackbody temperature if the

peak in the SW spectrum is displaced from its current position of 0.48

/xm to a yellower wavelength of 0.55/zm.

8.4. Orbital ellipticity brings the earth some 3.5% nearer the sun during Jan-

uary than during July, which is responsible for the slight asymmetry of

insolation apparent in Fig. 1.28. (a) Calculate the corresponding change

in the earth's equivalent blackbody temperature. (b) Discuss this change

in relation to other changes that are introduced by hemispheric asym-

metries of the earth's surface and atmospheric circulation.

8.5. Consider a 250 K isothermal atmosphere that contains a single absorbing

gas of uniform mixing ratio 0.05. The specific absorption cross section

of that gas is given as a function of wavelength by

trax--a'Oexp[-(A-A~ la [m2kg-1]'

where A 0 = 0.5/zm and a = 0.01/zm. (a) Calculate, as a function of A,

the optical path length for downward-traveling radiation from the top of

254 8 Atmospheric

Radiation

the atmosphere to the height z. (b) Plot the absorptivity of this layer, as

a function of h, for z = 5, 3, and 1 scale heights.

8.6. Show that a layer having optical thickness Au << 1 has absorptivity

Aa - Au.

8.7. Prove Kirchhoff's law (8.16) in generality.

8.8. The top of the photosphere has a radius of 7.0 x 108 m. If the mean

earth-sun distance is 1.5 x 1011 m, calculate the equivalent blackbody

temperature of the photosphere.

8.9. Venus has an albedo of 0.77 and a mean distance from the sun of 1.1 x

1011 m. (a) Calculate the equivalent blackbody temperature of Venus.

(b) Discuss this value in relation to the observed surface temperature of

750 K.

8.10. Consider an isothermal atmosphere that is optically thick to LW radia-

tion. (a) How much of the LW radiance emitted to space at zero zenith

angle originates in its uppermost three optical depths? (b) Determine

the altitude range, in scale heights, occupied by the layer between optical

depths of 0.1 and 3.0 under isothermal conditions.

8.11. A fiat plate sensor on board a satellite behaves as a graybody with

constant absorptivity a. Calculate its radiative-equilibrium temperature

when the sensor faces the sun if (a) a - 0.8 and (b) a - 0.2.

8.12. As for Problem 8.11, but if the sensor has different absorptivities to SW

and LW radiation of (a)

asw

and

aLW,

respectively, and (b)

asw

= 0.2

and

aLW

= 0.8.

8.13. Under the conditions of Problem 8.12, calculate the sensor's temperature

as a function of time after the satellite has been rotated to face the sensor

away from the sun, if it has an area of 0.1 m 2 and a specific heat of 2

jK -1.

8.14. The hood of an automobile can be modeled as a gray flat plate with LW

absorptivity 0.9 and the atmosphere as a gray layer with LW absorptivity

0.8. In this framework, estimate the hood's temperature for a solar zenith

angle of 25 ~ if (a) the automobile's color is light with a SW absorptivity

of 0.2 and (b) the automobile's color is dark with a SW absorptivity of

0.6. (c) What physical process would, in practice, mediate the values in

parts (a) and (b)?

8.15. A simple model approximates the earth's surface as a graybody and the

atmosphere as a gray layer with LW absorptivities of 1.0 and 0.8, respec-

tively. Use this model to estimate the radiative-equilibrium temperature

of the ground in the presence of 50% cloud cover (fully reflective) and

under (a) perpetual summertime conditions over vegetated terrain: a so-

lar zenith angle of 25 ~ and the surface having a SW absorptivity of 0.6,

and (b) perpetual wintertime conditions over snow-covered terrain: a

Problems

255

8.16.

8.17.

8.18.

8.19.

8.20.

8.21.

8.22.

8.23.

solar zenith angle of 60 ~ and the surface having a SW absorptivity of

0.2.

Consider a simple model of the earth comprised of an isothermal gray

layer with SW and LW absorptivities

asw

and

aLw,

respectively, and a

black underlying surface, both of which are illuminated by a SW flux F 0

and are in thermal equilibrium. The energy budget can be formulated

by tracing energy through repeated absorptions and reemissions by the

surface and atmosphere. (a) Develop an arithmetic progression for the

fractional energy absorbed by the atmosphere during successive trans-

missions from the surface to construct a series representation for the net

energy absorbed by the atmosphere. (b) Use the series representation

to calculate the radiative-equilibrium temperature of the atmosphere

for F 0 - (1-

d)(Fs/4 )

= 240 W m -2 (Sec. 1.3),

asw -

0.20, and

aLw -0.94,

which are representative of values in Fig. 1.27.

Use the results of Problem 8.16 to determine the radiative-equilibrium

temperature of the surface (a) for the conditions given, (b) in the absence

of an atmosphere, and (c) as in part (a), but with the atmosphere's LW

absorptivity increased to

aLw -0.98.

Estimate the level where the collisional half-width equals the Doppler

half-width for (a) the water vapor absorption line (Fig. 8.11) at A -1 -- 352

cm -1 and (b) the CO2 absorption line at A -1 - 712

cm -1.

Consider a discretely stratified atmosphere comprised of N isothermal

layers, each of which is transparent to SW radiation but has a LW ab-

sorptivity a and which, collectively, are in radiative equilibrium with an

incident SW flux F 0 and a black underlying surface. (a) Derive expres-

sions for the flux

emitted by the surface for N - 1, N - 2, and

then generalize those expressions to arbitrary N. (b) Let

a - 'rs/N

and

take the limit N --+ ~ to recover expression (8.81) for a continuously

stratified atmosphere. (c) Verify that, even though they have different

optical characteristics, the atmospheres for different N all have the same

equivalent blackbody temperature. Explain why.

Derive expressions (8.38) for the upwelling and downwelling intensities

in a plane parallel atmosphere as functions of optical depth.

Show that the upwelling and downwelling fluxes for horizontally isotropic

radiation are described in terms of the exponential integral E 2 by (8.45).

An 80% solar eclipse occurs during morning, when the tempera-

ture would normally be 20 ~ C. Use a gray atmosphere in radiative-

equilibrium with a black surface to estimate the change of surface

temperature that would result were the eclipse to persist indefinitely

(compare Problem 8.33).

Show that the two-stream transformation (8.54) casts the budgets of

upwelling and downwelling radiation into the form of (8.55).

256 8

Atmospheric

Radiation

8.24.

8.25.

8.26.

8.27.

8.28.

8.29.

Consider a gray atmosphere that is moisture laden, in hydrostatic equilib-

rium, and has a LW specific absorption coefficient k. The atmosphere is

in radiative equilibrium with a black surface, which, in turn, is in thermal

equilibrium with a downwelling SW flux F 0. (a) Provide an expression

relating the radiative-equilibrium temperature TeE to height z. Discuss

the form of this relationship and how it can be solved for TRe(Z). (b)

Determine TRe(Z) in a neighborhood of the surface if the atmosphere

is optically thick (e.g., in the limit k --+ c~) and if the relative change of

temperature there can be ignored. (c) Under the conditions of part (b)

but in light of hydrostatic stability and if air near the surface is almost

saturated, derive an expression involving the height of the tropopause.

Discuss how the tropopause height depends on surface temperature and

the physical processes controlling it.

Consider a gray atmosphere with a LW specific absorption coefficient k

and an underlying surface with SW and LW absorptivities asw and aLW,

respectively. (a) Determine the distribution of radiative-equilibrium

temperature as a function of optical depth, asw, and aLW. (b) For

aLW = 1, discuss the limiting behavior: asw ~ O. (c) For asw = 1,

discuss the limiting behavior: aLw ~ O.

Discuss how the competing influences of radiative transfer and con-

vective mixing control stratification, in light of the diurnal variation of

insolation.

Show that the upwelling flux inside a gray atmosphere that is in radiative

equilibrium with a black underlying surface is given by (8.71).

Revisit the radiative-convective equilibrium in Figs. 8.21 and 8.22. (a)

Determine the temperature distribution under the same conditions, but

now using the CAPE (Sec. 7.4.1) of the radiative equilibrium atmosphere

to infer the tropopause height zT and presuming the air to be virtually

saturated. (b) Plot the profiles of upwelling and downwelling fluxes under

this radiative-convective equilibrium. (c) Plot the profile of radiative

heating.

The Venusian atmosphere is composed chiefly of carbon dioxide, with

g = 8.8 m s -2, Cp = 8.44 • 102 J kg -1

K -1

for CO2, a mean distance

from the sun of 0.70 that of Earth, and an albedo of d = 0.77. (a) Use

radiative equilibrium and the observed surface temperature Ts = 750 K

to estimate the optical depth of the Venusian atmosphere. (b) Calcu-

late the temperature distribution under radiative-convective equilibrium

based on (1) the profile of optical depth (8.69), with h = RTs/g, (2)

the presumption that temperatures inside the convective layer are hot

enough to ignore condensation, and (3) in place of the constraint used

in Sec. 8.5.2 to determine the tropopause height, requiring the temper-

ature at the midlevel of the hydrostatically unstable layer to equal that

Problems 257

8.30.

8.31.

8.32.

8.33.

8.34.

under radiative equilibrium. (c) Plot the profiles of upwelling radiation,

downwelling radiation, and radiative heating.

The CO2 absorption band is already saturated in the earth's atmosphere

(Fig. 8.1). In light of this feature, explain how increased levels of CO2

could result in global warming.

Derive the expression for Newtonian cooling (8.79) from the full repre-

sentation of radiative heating.

(a) Calculate the characteristic timescale of thermal damping in the

troposphere based on P0 = 1.2 kg

m -3,

the equivalent blackbody tem-

perature

T e

= 255 K (which is symbolic of where most OLR is emitted),

and a characteristic depth of 5 km (which corresponds to the preced-

ing temperature under radiative-convective equilibrium: Fig. 8.21). (b)

What is the heat capacity of the surface under this approximation?

Use Newtonian cooling in Problem 8.32 to estimate the amplitude

ATs

of the diurnal cycle of surface temperature, where AT~ is approximated

by half the nocturnal depression of temperature from its daytime maxi-

mum. Estimate

ATs

under equinoctial conditions, for a surface temper-

ature maximum of 300 K, and for an optical depth (a) ~'s = 4, which is

representative of the global-mean conditions, and (b) ~s = 1, which is

representative of arid conditions.

Construct a counterpart to Fig. 8.30 for the runaway greenhouse effect,

using the same initial values but based on radiative equilibrium. At what

temperature does the earth's atmosphere become saturated? Compare

this value with the one obtained under radiative-convective equilibrium.

Chapter 9

Aerosol and Clouds

Radiative transfer is modified importantly by clouds. Owing to their high

reflectivity in the visible, clouds shield the earth-atmosphere system from so-

lar radiation and thus represent cooling in the shortwave (SW) energy budget.

Conversely, the strong infrared (IR) absorptivity of water and ice particles

sharply increases the optical depth of the atmosphere, which magnifies the

greenhouse effect and represents warming in the longwave (LW) energy bud-

get. Atmospheric aerosol has optical properties similar to clouds.

We develop cloud processes from a morphological description of atmo-

spheric aerosol, without which clouds would not form in the earth's atmo-

sphere. We then examine the microphysics controlling cloud formation. Macro-

physical characteristics of clouds and accompanying microphysical properties

are developed in terms of environmental conditions controlling the formation

of particular cloud types. These elemental considerations culminate in descrip-

tions of radiative and chemical processes that operate inside clouds and figure

in climate.

9.1 Morphology of Atmospheric Aerosol

Small particulates are produced and removed through a variety of processes,

which make the composition, size, and distribution of atmospheric aerosol

widely variable (Table 9.1). Aerosol concentrations are smallest over the

oceans (Fig. 1.22), where a particle number density of n

= 10 3 cm -3

is repre-

sentative, and greatest over industrial areas, where n > 105 cm -3 is observed.

These and other distinctions lead to two broad classes of tropospheric aerosol:

continental

and

marine.

9.1.1 Continental Aerosol

Continental aerosol includes (1) crustal species that are produced by ero-

sion of the earth's surface, (2) combustion and secondary components related

to anthropogenic activities, and (3) carbonaceous components consisting of

hydrocarbons and elemental carbon. Crustal aerosol is produced in subtrop-

ical deserts like the Sahara, the southwestern United States, and southern

258

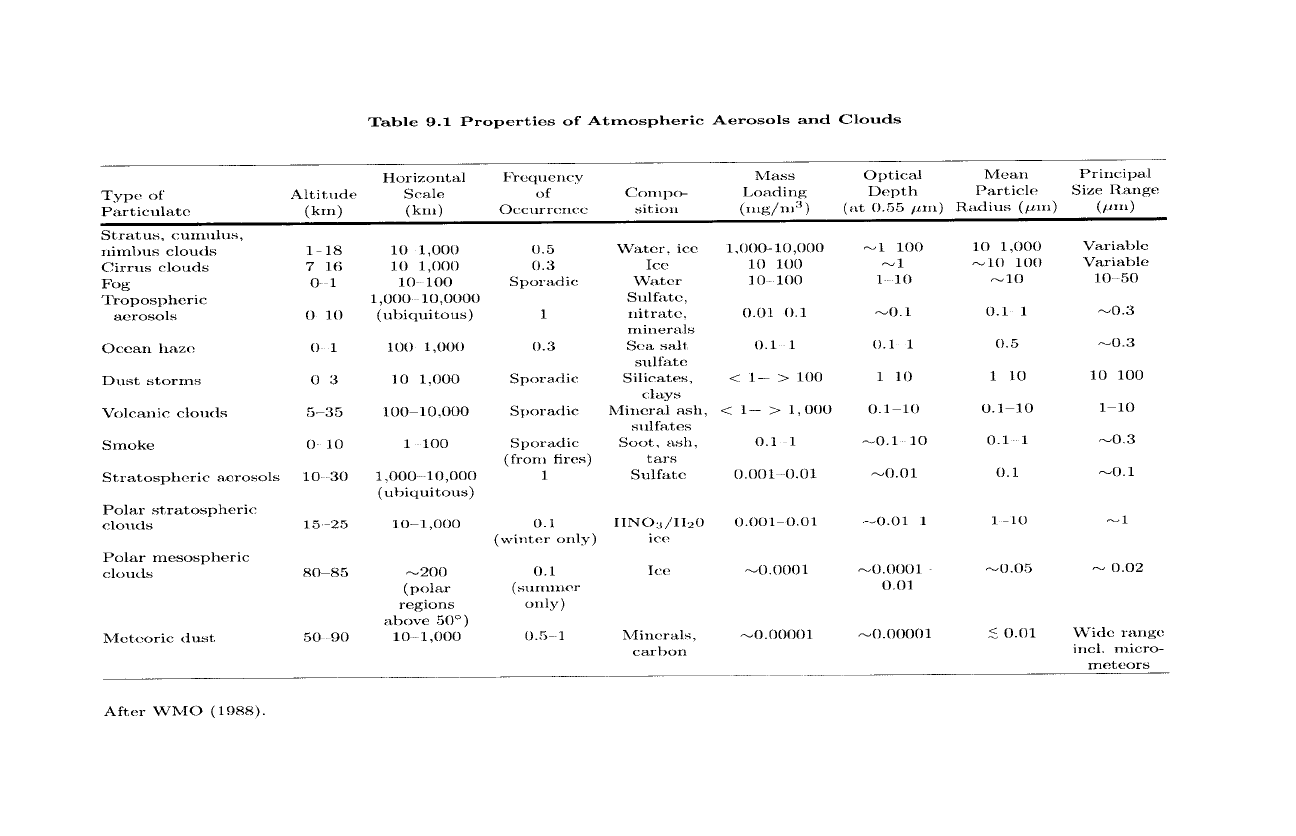
Table

9.1

Properties

Atmospheric

Aerosols and

Clouds

Horizontal

Frequcricy

&lass

Optical

Mean

Principal

Typc.

Altitude

Scale

C"n1p"-

Depth

Particlr Size Range

Particulatc

(krri)

(kiii)

Occurronw

sitioii

(riig/~ii")

(at

0.55

/LII~)

Radius

(,uiri)

(/mi)

Stratus,

ciirnrilus.

Iiimbiis

clouds

Cirnis

cloiids

Fog

Tropospheric

aerosols

Occari

hazc

Dust

storms

Volcanic

cloricls

Smoke

Stratosphcric

a.crosols

Polar stratosphcric

clo11ds

Polar

mesospheric

Cl<>ll<lS

blct voric dust,

5-35

15-25

80-85

1,000

10 1,000

100

1,000

10,0000

(ubiquitous)

100

1,000

1.000

100-10,000

100

1.000

10,000

(ubiquitous)

10-1,000

0.5

0.3

Sporadic

0.3

Sporadic

(fronl

fircs)

0.1

Water.

ice

Icc.

Wittcr

Sulfate,

nitrate.

minerals

Sca

salt

s11lfate

Silicates,

clays

Mincral ash,

SlllfiLtCS

Soot,

ash.

tars

Sulfatc

1.000-10,000

100

10 100

I-

100

000

0.001

0.01

0.00

1-0.0

(winter

orlly)

ic?

-200

0.1

ICY.

-0.000

(polar

(siirni

iicr

regions

o11ly)

above

SOo)

1,000

0.5-

Miricrals,

-0.00001

carbon

-1

100

-1

110

-0

0.1 1

110

1-10

-01

-0.01

-0 .0

-0

0001

-0

.oooo

1,000

-10

100

-10

0.1

0.5

0.1-10

0.1

1-10

0.05

0.01

Variable

10 50

-0.3

10 100

1-10

-0.3

-0.1

--I

0.02

Widc

raiipc

irlcl. micro-

meteors

After

WMC>

(

1988).