Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

150 6 Hydrostatic Equilibrium

9 ... ....~.

::-......v:i:;,~:.,.,.:~ "~' 9

.....

.....;?" -/

281

"'" i Z

' !

/ J P

...,

~ooOO .oOOO~ ......... .o,.,oOr

O,.o ..-

":......

\ .... .... ...... 9 j .::"

9 .. "', ...... 9 .........

"'~', ""~...

"'"-... H ~.

.........

2{34. "

..... ""

""""--. ............. ~~176176

:..."

....

:...

"~',, ...'"

~"~i ........ " :::

-:;> ./

!~. ........... ii

9 "............-""

s ~

........... " .........

.... ,.~:; ..... ....

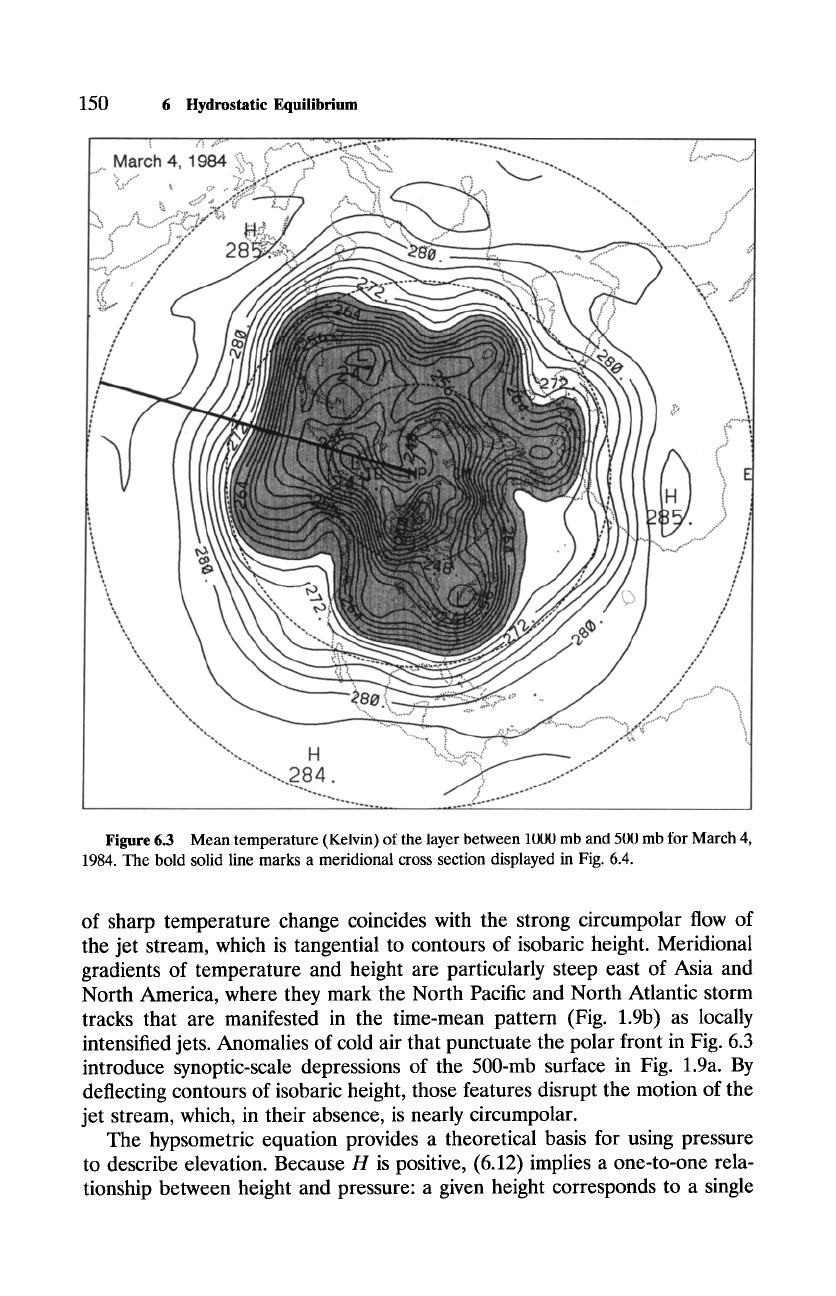
Figure 6.3 Mean temperature (Kelvin) of the layer between 1000 mb and 500 mb for March 4,

1984. The bold solid line marks a meridional cross section displayed in Fig. 6.4.

of sharp temperature change coincides with the strong circumpolar flow of

the jet stream, which is tangential to contours of isobaric height. Meridional

gradients of temperature and height are particularly steep east of Asia and

North America, where they mark the North Pacific and North Atlantic storm

tracks that are manifested in the time-mean pattern (Fig. 1.9b) as locally

intensified jets. Anomalies of cold air that punctuate the polar front in Fig. 6.3

introduce synoptic-scale depressions of the 500-mb surface in Fig. 1.9a. By

deflecting contours of isobaric height, those features disrupt the motion of the

jet stream, which, in their absence, is nearly circumpolar.

The hypsometric equation provides a theoretical basis for using pressure

to describe elevation. Because H is positive, (6.12) implies a one-to-one rela-

tionship between height and pressure: a given height corresponds to a single

6.4 Stratification 151

pressure. Therefore, pressure can be used as an alternative to height for the

vertical coordinate. Isobaric coordinates, which are developed in Chapter 11,

use surfaces of constant pressure for coordinate surfaces. Although they evolve

with the circulation, isobaric coordinates afford several advantages.

In isobaric coordinates, pressure becomes the independent variable and

the height of an isobaric surface becomes the dependent variable, for exam-

ple, z2 =

z(x, y,

P2). Because pressure decreases monotonically with height,

low height of an isobaric surface corresponds to low pressure on a surface of

constant height and just the reverse for high values (Fig. 6.2). For the same

reason, contours of isobaric height resemble isobars on a surface of constant

height. Consequently, the horizontal distribution of isobaric height may be in-

terpreted analogously to the distribution of pressure on a surface of constant

height. From hydrostatic equilibrium, the latter represents the weight of the

atmospheric column above a given height. Therefore, the distribution of iso-

baric height reflects the horizontal distribution of atmospheric mass above the

mean elevation of that isobaric surface.

Contours of 500-mb height that delineate the polar front in Fig. 1.9a cor-

respond to isobars on the constant height surface: z ,~ 5.5 km, with pressure

decreasing toward the pole. Thus, less atmospheric column lies above that el-

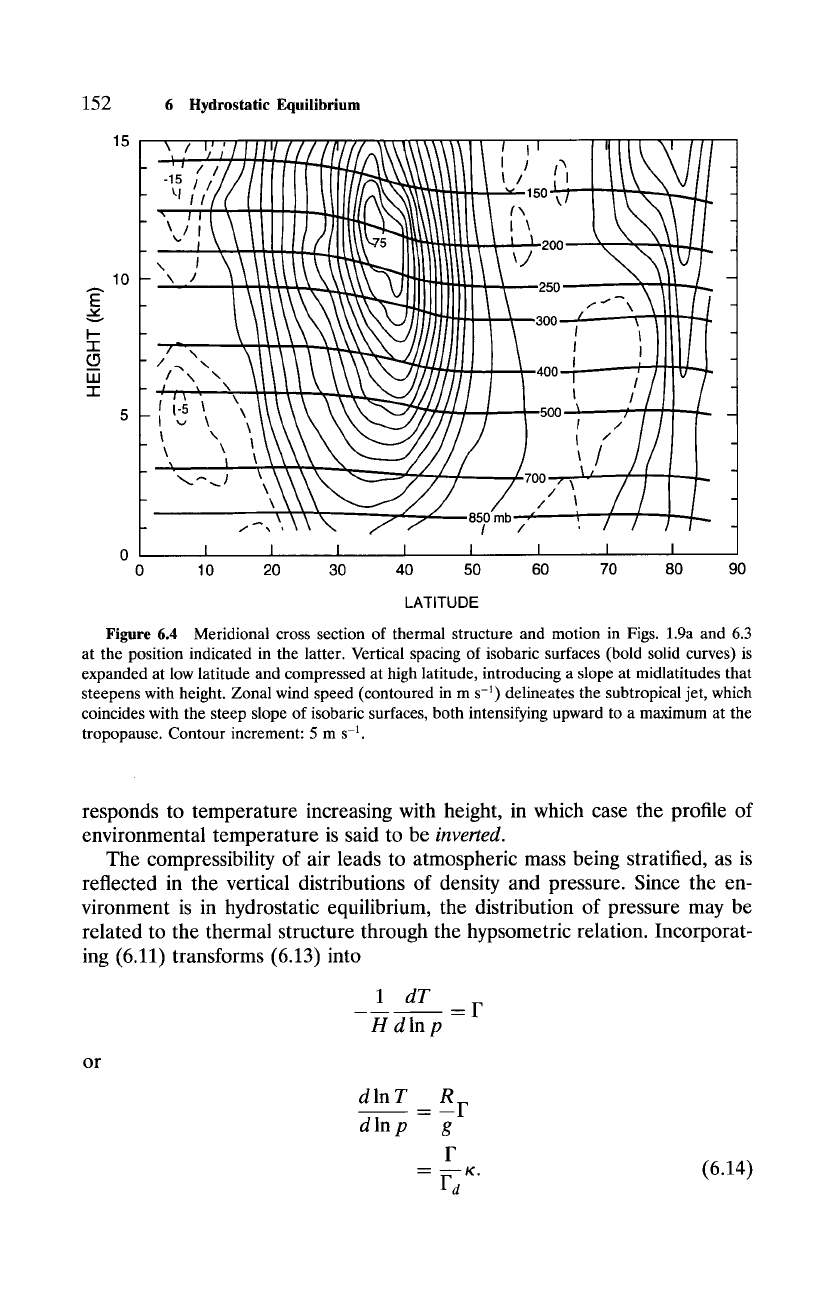
evation poleward of the front than equatorward of the front. Figure 6.4 shows

a meridional cross section of the thermal structure and motion in Figs. 6.3

and 1.9a. The horizontal distribution of mass just noted results from compres-

sion of isobaric surfaces poleward of the front, which is centered near 40 N, and

expansion equatorward of the front. This introduces a tilt to isobaric surfaces at

midlatitudes, one that steepens with height. The jet stream is found in the same

region and likewise intensifies vertically, to a maximum near the tropopause.

Similar behavior at high latitudes marks the base of the polar-night jet.

6.4 Stratification

Expressions (2.33) and (5.32) for the dry adiabatic and saturated adiabatic

lapse rates, which describe the evolution of a displaced air parcel under unsat-

urated and saturated conditions, respectively, hold formally with z representing

geopotential height and g constant. Neither Fa nor Fs has a direct relation-

ship to the temperature of the surroundings because a displaced parcel is

thermally isolated under adiabatic conditions. Thermal properties of the en-

vironment are dictated by the history of air residing at a given location, for

example, by where that air has been and what thermodynamic influences have

acted on it. The

environmental lapse rate

is defined as

dz'

(6.13)

where T refers to the ambient temperature. Like parcel lapse rates, F > 0

corresponds to temperature decreasing with height. Conversely, F < 0 cor-

152 6

Hydrostatic Equilibrium

's ~ ii r

. l~ I

10 - \ / l

" i'2-,,-

, ~, llI\\\\\\\",,,",V-JlIIIIlflTT-TT" -,,

',/Ill/"t"

~,,. \/\\\v~-~xd~///lll

I \ ,

]

!!III i

m .I ,, ",. \~\~\ \\\\x,-J/777/7/1--t-"~4~176 / III v 7"

: ._ ,,

I1111\- I /

~g ,, ',//t\',,\~///

L,oo_, ,'/!1

",, )

{,"lll

'-/'jj/-

/._,\

8$Omb~.

t //

/i ~'"

I I I I I I I

0 10 20 30 40 50 60 70 80 90

LATITUDE

Figure 6.4 Meridional cross section of thermal structure and motion in Figs. 1.9a and 6.3

at the position indicated in the latter. Vertical spacing of isobaric surfaces (bold solid curves) is

expanded at low latitude and compressed at high latitude, introducing a slope at midlatitudes that

steepens with height. Zonal wind speed (contoured in m s -1) delineates the subtropical jet, which

coincides with the steep slope of isobaric surfaces, both intensifying upward to a maximum at the

tropopause. Contour increment: 5 m s -1.

responds to temperature increasing with height, in which case the profile of

environmental temperature is said to be

inverted.

The compressibility of air leads to atmospheric mass being stratified, as is

reflected in the vertical distributions of density and pressure. Since the en-

vironment is in hydrostatic equilibrium, the distribution of pressure may be

related to the thermal structure through the hypsometric relation. Incorporat-

ing (6.11) transforms (6.13) into

1 dT

H dlnp

din T

dln p

=~r

(6.14)

6.4 Stratification

153

6.4.1 Idealized Stratification

For certain classes of thermal structure, (6.14) can be integrated analytically

to obtain the distributions of pressure and other thermal properties inside an

atmospheric layer.

LAYER OF CONSTANT LAPSE RATE

F -

const ~- 0, (6.14) yields

T = (-~~) ~K Ts , (6.15)

where the subscript s refers to the base of the layer. Because

T(z) = T s - rz,

(6.16)

(6.15) can be used to obtain the vertical distribution of pressure:

PPs

-[1- K-~F (ZHss)] (~r) . (6.17)

Then (2.31) implies the vertical profile of potential temperature:

F d

O(z, - (T s

- Fz)[l -K F---aF (~ss)] r , (618).

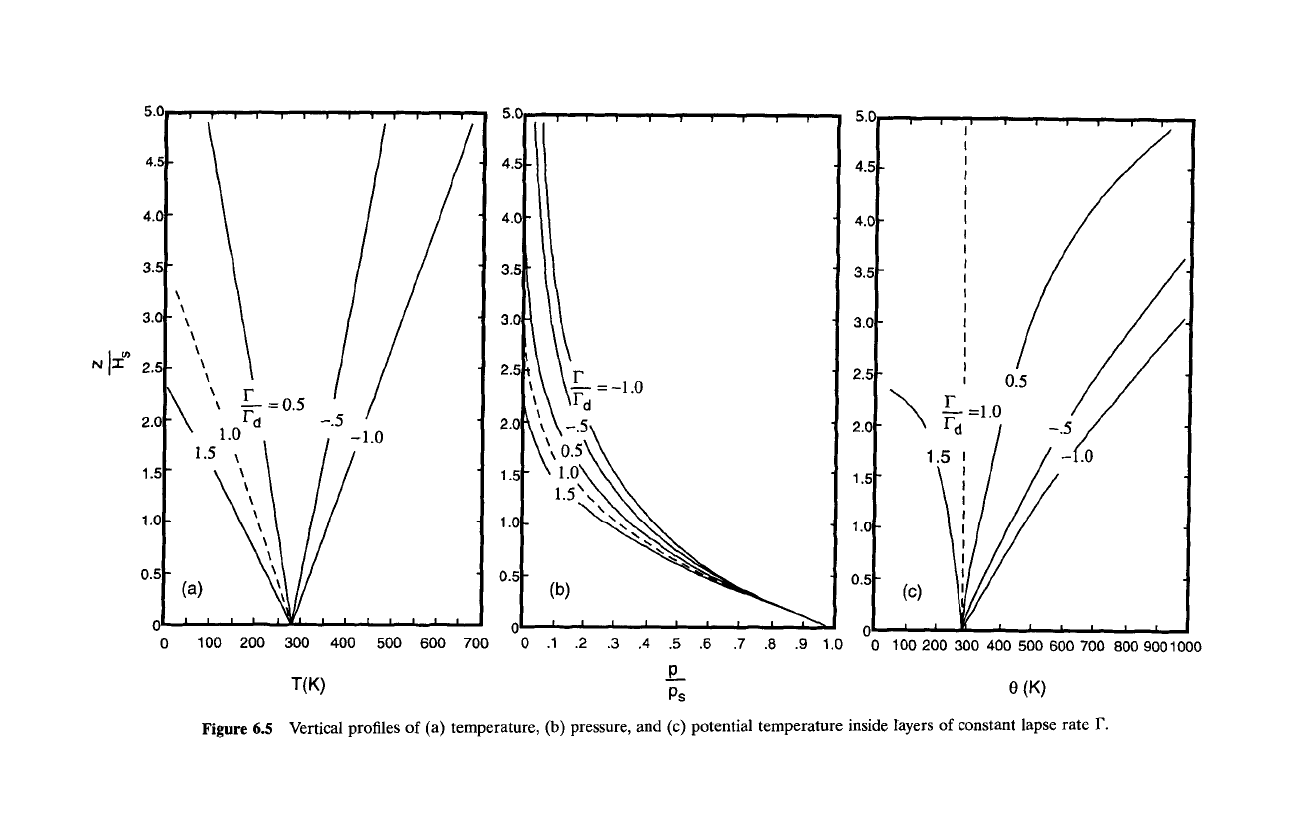
where p~ - P0 = 1000 mb has been presumed for the base of the layer.

As shown in Fig. 6.5, the compressibility of air makes pressure decrease

with height for all F. The same is true of density. However, potential temper-

ature decreases with height only for F > F a, whereas it increases with height

for F < Fa. In both cases, 0 varies sharply with height because the pressure

term dominates over the temperature term in determining the height depen-

dence in (6.18). As a result, environmental potential temperature can change

by several hundred degrees in just a few scale heights, as is typical in the

stratosphere (refer to Fig. 17.19). By contrast, the potential temperature of a

displaced air parcel is independent of its height under adiabatic conditions.

The thermal structure described by (6.16) through (6.18) can apply lo-

cally (e.g., inside a certain layer), even if temperature does not vary linearly

throughout the atmosphere. Should it apply for the entire range of height,

(6.16) has one further implication. For F > 0, positive temperature requires

the atmosphere to have a finite upper bound

Zto p -- -~-, (6.19)

where p vanishes. For F < 0, no finite upper bound exists.

I="

2.'

O.!

100

200 300

400

500

600 700

1.0

100

200

300

400

500

600

700

8009001000

(K)

T(K)

Figure

6.5

Vertical profiles

(a) temperature,

(b)

pressure, and (c) potential temperature inside rayers

constant lapse rate

6.5

Lagrangian Interpretation of Stratification

155

ISOTHERMAL LAYER

For the special case F - 0, (6.17) is indeterminate. Reverting to the hydro-

static relation (6.11) yields

z=-Hln (-~~)

-- e ~, (6.20)

which is identical to (1.17) under these circumstances. Then the vertical profile

of potential temperature is simply

O(z) = Tse"~

: 0se~. (6.21)

Under isothermal conditions, environmental potential temperature increases

by a factor of e every K -a --- 3 scale heights.

ADIABATIC LAYER

For the special case F = Fa, (6.15) reduces to

T K

-T-~ - (-~s) (6.22,

and the distribution of pressure (6.17) becomes

P 1- . (6.23)

Equation (6.22) is the same relationship between temperature and pressure

implied by Poisson's equation (2.30.2), which defines potential temperature

(2.31). Accordingly, the vertical profile of potential temperature (6.18) re-

duces to

O(z) - O~ -

const (6.24)

inside this layer.

6.5 Lagrangian Interpretation of Stratification

As noted earlier, hydrostatic equilibrium applies in the presence of motion

as well as under static conditions. Therefore, each of the stratifications in

156 6

Hydrostatic Equilibrium

Sec. 6.4 is valid even if a circulation is present, as is invariably the case. Under

those circumstances, vertical profiles of temperature, pressure, and potential

temperature [(6.16) through (6.18)] correspond to the horizontal-mean ther-

mal structure and hence to averages over many ascending and descending air

parcels. Interpreting thermal structure in terms of the behavior of individ-

ual air parcels provides some insight into the mechanisms controlling mean

stratification.

For a layer of constant lapse rate, the relationship between temperature

and pressure (6.15) resembles one implied by Poisson's equation (2.30.2), but

for a polytropic process (Sec. 2.5.1) with

(F/Fd)K

in place of K. Consequently,

we can associate the thermal structure in (6.16) through (6.18) with a vertical

rearrangement of air in which individual parcels evolve diabatically according

to a polytropic process. In that description, air parcels moving vertically ex-

change heat with their surroundings in such proportion for their temperatures

to vary linearly with height. For an individual air parcel, the foregoing process

has a polytropic specific heat that satisfies

R F

(cp -c) rd

C-

1- --F--- . (6.25)

The corresponding heat transfer for the parcel is then given by (2.37) and its

change of potential temperature follows from (2.40).

6.5.1 Adiabatic Stratification

Consider a layer characterized by

V = V a, (6.26.1)

the stratification of which is termed

adiabatic.

Then (6.25) implies

C=0,

(6.26.2)

6q - dO - O,

so individual air parcels evolve adiabatically. Under these circumstances, air

parcels move vertically without interacting thermally with their surroundings.

Such behavior can be regarded as the limiting situation when vertical motion

occurs on a timescale that is short compared to diabatic effects, as is typical of

cumulus and sloping convection. Although their vertical motion is adiabatic,

individual parcels may still exchange heat at the boundaries of the layer. In

6.5

Lagrangian Interpretation of Stratification

157

fact, such heat transfer is necessary to maintain vertical motion in the absence

of mechanical forcing.

The evolution of an individual parcel can be envisaged in terms of a circuit

that it follows between the upper and lower boundaries of the layer, where

heat transfer is concentrated. Such a circuit is depicted in Fig. 6.6 for a layer

representative of the troposphere. At the lower boundary, an individual par-

cel moves horizontally long enough for heat transfer to occur. Isobaric heat

absorption [e.g., through absorption of longwave (LW) radiation and transfer

of sensible heat from the surface] increases the parcel's potential temperature

(Fig. 6.7a). The accompanying increase of temperature (Fig. 6.7b) causes the

parcel to become positively buoyant and rise. If the timescale of vertical mo-

tion is short compared to that of heat transfer, the parcel ascends along an

adiabat in state space until it reaches the upper boundary, where it again moves

horizontally. Isobaric heat rejection (e.g., through LW emission to space) then

decreases the potential temperature and temperature of the parcel, which

therefore becomes negatively buoyant. The parcel then sinks along a different

adiabat until it has returned to the surface and completed a thermodynamic

cycle.

If it remains unsaturated [e.g., below its lifting condensation level (LCL)],

each air parcel comprising the layer preserves its potential temperature away

from the boundaries. Consequently, each parcel traces out a uniform profile

of 0 as it traverses the layer. The horizontal-mean potential temperature

O(z)

is equivalent to an average over all such parcels at a given elevation, so it is

likewise independent of height, that is,

O(z) -

const. (6.27.1)

q<O

--~m,-~-- ~ ~ ~ -

-1~ ~ ~~ -- --q~ ~ --~m ~

I I

.~._ m __..~.._ __ ~.~[... m m-4b-- m ~..~- ~ ~ -~- ---.~--~

q>O

Figure

6.6 Idealized circuit followed by an air parcel during which it absorbs heat at the base

of a layer and rejects heat at its top, with adiabatic vertical motion between.

158

6 Hydrostatic Equilibrium

(a)

q<O

r~- -- -- .~-t~.~- I

q>O

(b)

#q<O

\ .... _-~-~. \

'..... \

\ ',, =

IL --T \\

rd~ ",. \.

\ ',,

\ ",, \

\ ".... \~

\ "--,, \

\ '.... \

-- ~-1~ : -1~

....

~ q>O

T v

Figure 6.7 Thermodynamic cycle fol-

lowed by the air parcel in Fig. 6.6 in terms

of (a) potential temperature and (b) temper-

ature. Horizontally averaged behavior for a

layer composed of many such parcels is also

indicated by the dotted lines.

As is true for an individual parcel (Sec. 2.4.2), a uniform distribution of po-

tential temperature corresponds to a constant environmental lapse rate

F- F a. (6.27.2)

Consequently, the thermal structure associated with (6.24) can be interpreted

as the horizontal mean for a layer in which air is being actively and adiabati-

cally rearranged in the vertical.

This interpretation can be extended to saturated conditions (e.g., inside

cloud). An air parcel's evolution is then pseudo-adiabatic, so its equivalent

potential temperature is conserved. Active vertical rearrangement_of air will

then make the horizontal-mean equivalent potential temperature

Oe(z)

inde-

pendent of height

Oe(Z ) =

const. (6.28.1)

6.5

Lagrangian Interpretation of Stratification

159

From Sec. 5.4.3, this uniform distribution of

Oe(Z )

corresponds to a mean

environmental lapse rate

V = F,, (6.28.2)

the corresponding stratification being termed

saturated adiabatic.

Even though all parcels inside the layer evolve in like fashion, local be-

havior will differ from the horizontal mean because conserved properties may

still vary from one parcel to another (e.g., due to different histories experi-

enced by those parcels at the layer's boundaries). An ascending parcel will

have values of 0 and 0e, which are greater than the corresponding horizontal-

mean values because that parcel will have recently absorbed heat at the lower

boundary. Conversely, a descending parcel will have values of 0 and 0e, which

are less than the corresponding horizontal-mean values because that parcel

will have recently rejected heat at the upper boundary. Therefore, the actual

stratification of the layer will vary with horizontal position.

If heat transfer at the boundaries were to be eliminated, convectively driven

motions would then "spin down" through turbulent and molecular diffusion

toward a limiting state of no motion. Since diffusion destroys gradients be-

tween individual parcels, this limiting state is characterized by homogeneous

distributions of 0 and 0e and thus, everywhere, by the environmental lapse

rate F -- F d or F s. Hence, this limiting homogeneous state has stratifica-

tion identical to the horizontal-mean stratification of the layer being con-

vectively overturned, which may therefore be regarded as "statistically well

mixed."

The stratification (6.28) is characteristic of the troposphere. Close to the

saturated adiabatic lapse rate (Fig. 1.2), the mean thermal structure in the

troposphere follows from efficient vertical exchange of moist air inside cu-

mulus and sloping convection. Air rearranged by convection is continually

replenished with moisture through contact with warm ocean surfaces. Because

convective motions operate on timescales of a day or shorter, they make the

troposphere statistically well mixed and, in the mean, described approximately

by (6.28).

In traversing the circuit, the parcel in Fig. 6.7 absorbs heat at high temper-

ature and rejects heat at low temperature. By the second law (Sec. 3.2), net

heat is absorbed over a cycle. Then the first law (2.13) implies that the parcel

performs net work during its traversal of the circuit. It follows that an indi-

vidual parcel in the above circulation behaves as a heat engine. In fact, the

thermodynamic cycle in Fig. 6.7 is analogous to the Carnot cycle pictured in

Fig. 3.2, except that heat transfer occurs (approximately) isobarically instead

of isothermally. More expansion work is performed by the parcel during ascent

than is performed on the parcel during descent. The area circumscribed by

the parcel's evolution in Fig. 6.7b reflects the net work it performs during the