Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

120 5

Transformations of Moist

Air

from which the dimensionless quantities 3' and K (2.21) follow directly. Like

virtual temperature,

co, Cp, y,

and K differ only slightly from the constant

values for dry air.

5.1.2 Saturation Properties

Consider now the gas phase of the system in the presence of a condensed

phase of water. If the vapor is in chemical equilibrium with the condensed

phase, it is said to be

saturated.

Corresponding to this condition and for a

given pressure and temperature are particular values of the foregoing moisture

variables, which are referred to as

saturation values.

According to the Gibbs-

Dalton law, the

saturation vapor pressure

with respect to water

is identical

to the equilibrium vapor pressure Pw of a single-component system of vapor

and water (Sec. 4.6). Likewise, the saturation vapor pressure with respect to

ice

e i

is identical to

for a single-component system. 2

The saturation vapor pressure

ec,

where c denotes either of the condensed

phases, is a function of temperature alone and described by the Clausius-

Clapeyron relations (4.39) and (4.40). The

saturation specific humidity qc

and

the

saturation mixing ratio r c,

which follows from

through (5.7), also describe

the abundance of vapor at equilibrium with a condensed phase. Like the

saturation vapor pressure, these quantities are state variables. But, because

they refer to the mixture and not just the vapor,

and

r c

also depend on

pressure, in accord with Gibbs' phase rule (4.24) for a two-component system

involving two phases. However, the strong temperature dependence of

ec(T)

in the Clausius-Clapyeron equation is the dominant influence on

qc(P, T)

and

rc( p, T).

Therefore, a decrease of temperature following from adiabatic

expansion sharply reduces the saturation values

and

r c.

Just the reverse

results from an increase of temperature following from adiabatic compression.

Contrary to saturation values, which change with the thermodynamic state

of the system, the abundance of vapor actually present changes only through

a transformation of phase. If no condensed phase is present (e.g., under un-

saturated conditions), the abundance of vapor is preserved. A decrease of

temperature then results in a decrease of

rc,

but no change of r. On the other

hand, if the system is saturated, r =

rc( p,

T). A change of state in which the

system remains saturated must then result in a change of both

rc(p, T)

and r,

that is, the vapor and condensate must adjust to preserve chemical equilibrium

between those phases.

Strictly, the water component of the two-component system does not behave exactly as it would

in isolation. Discrepancies in that idealized behavior stem from (1) near saturation, departures

of the vapor from the behavior of an ideal gas, (2) the condensed phase being acted on by the

total pressure and not just that of the vapor, and (3) some of the air passing into solution with

the water. However, these effects introduce discrepancies that are smaller than 1%, so they can

be ignored for most applications; see Iribarne and Godson (1981) for a detailed treatment.

5.2 Implications for the Distribution of

Water Vapor

121

Two other quantities are used to describe the abundance of water vapor.

The

relative humidity

is defined as

RH-- Nv

e r

= ___ , (5.13)

ec rc

where

N~c

denotes the saturation molar abundance of vapor, and equilibrium

with respect to water is usually implied. The

dew point Td

is defined as that

temperature to which the system must be cooled "isobarically" to achieve

saturation. If saturation occurs below 0~ that temperature is the

frost point

Tf.

The

dew point spread

is given by the difference

(T- Td).

For a given

temperature T, a high dew point implies a small dew point spread. Each cor-

responds to a large abundance of vapor, which requires only a small depres-

sion of temperature to achieve saturation.

Neither relative humidity nor dew point spread are direct measures of va-

por concentration but, rather, describe how far the system is from saturation.

Because saturation values increase sharply with temperature, inferring mois-

ture content from the aforementioned quantities is misleading. For instance,

r w at 1000 mb and 30~ is nearly 30 g kg -1, but only 4 g

kg -1 at

the same pres-

sure and 0~ Therefore, a relative humidity of 50% implies an abundance of

vapor of 2 g kg -~ in the latter but of 15 g kg -~ in the former~more than

seven times as large.

5.2 Implications for the Distribution of Water Vapor

Saturation values describe the maximum abundance of vapor that can be sup-

ported by air for a given temperature and pressure. At that abundance, dif-

fusion of mass from vapor to condensate is balanced by diffusion of mass in

the opposite sense. If the system is heterogeneous and has a vapor abundance

below the saturation value (e.g., an unsaturated air parcel in contact with a

warm ocean surface), vapor will be absorbed until the difference of chemical

potential between the phases of water has been eliminated. For this transfor-

mation to occur, the water component must absorb heat equal to the latent

heat of vaporization. Conversely, if the system is heterogeneous and has a va-

por abundance slightly above the saturation value (e.g., a supersaturated air

parcel containing an aerosol of droplets), vapor will condense to relieve the

imbalance of chemical potential. For this transformation to occur, the water

component must reject heat equal to the latent heat of vaporization.

At temperatures and pressures representative of the atmosphere, the satu-

ration vapor pressure seldom exceeds 60 mb and the saturation mixing ratio

seldom exceeds 30 g kg -1 or 0.030. It is for this reason that water vapor exists

122

Transformations of Moist

Air

only in trace abundance in the atmosphere. One should note that the foregoing

moisture properties refer only to vapormnot to the total water content of the

system. Condensation results in a reduction of q and r, but a commensurate

increase of condensate according to (4.6.2). Unless condensate precipitates

out of the system, the total water content of an air parcel is preserved.

According to the Clausius-Clapeyron equation, saturation vapor pressure

depends exponentially on temperature. Thus, air can support substantially

more vapor in solution at high temperature than at low temperature. For this

reason, water vapor is produced efficiently in the tropics, where warm sea

surface temperature (SST) corresponds to high equilibrium vapor pressure

(Fig. 5.1), and its mixing ratio decreases poleward (Fig. 1.14). Conversely,

water vapor is destroyed aloft through condensation and precipitation, after

displaced air parcels have cooled through adiabatic expansion work (2.33) and

suffered a sharp reduction of saturation mixing ratio. Condensation also occurs

at high latitudes, after displaced air parcels have cooled through radiative and

conductive heat transfer.

Production of vapor at an ocean surface can occur only if the water com-

ponent absorbs latent heat to support the transformation of phase. Absorbed

from the ocean or directly from shortwave radiation, that latent heat is then

transferred to the air with which the vapor passes into solution. When the

water recondenses, the latent heat is released to the air surrounding the con-

densate (Fig. 5.2) and remains in the atmosphere after the condensate has

precipitated back to the surface. Therefore, the preceding cycle results in no

permanent exchange of mass but a net transfer of heat from the ocean to the

atmosphere (see Fig. 1.27).

30E 60E 90E 120E 150E 180 150W 120W 90W 60W 30W 0 30E

90N 90N

60N

50N

30S

60S

60N

50N

30S

60S

90S 90S

30E 60E 90E 120E 150E 180 150W 120W 90W 60W 30W 0 30E

Figure

5.1 Global distribution of sea surface temperature (SST) for March. Temperatures

warmer than 28~ are shaded. From Shea

et al.

(1990).

5.3 State Variables of the Two-Component System

123

9 v9

\ 9 , .... ~: '~"::~. ~ ~. ~:~ .... ~:~ "ff '"::: " ~: "~$~i~i~,~'~ ,~:::~:

.... ~,::~,:!!.. ~ ~ .:~ .: .,.~ ..,~:~~iii~?ii?~i~i~ii!i~iil~,i~iiii~'~iiii!!~:~:i~ :: ....

" i

liiiii!!!4i !i!!

and Vapor

", 9 9 9 - '

" \ ~ o 9 00 ~ , 9 9 00 /

,['~ "l, r

"-.'. "" ".. ". ". ". ". 0-" //

Figure 5.2 Schematic illustration of a saturated air parcel undergoing condensation, in which

latent heat q is released to the gas phase and some of the condensate precipitates out of the

parcel.

5.3 State Variables of the Two-Component System

Under unsaturated conditions, the two-component system involves only a sin-

gle phase. By Gibbs' phase rule (4.24), the system then possesses three ther-

modynamic degrees of freedom. Thus, three intensive properties are required

to specify the system's state if no condensate is present. Usually, the state of

moist air is specified by pressure, temperature, and a humidity variable like

mixing ratio, for example, 0 =

O(p, T, r).

Under saturated conditions, two

phases are present and one of the independent state variables is eliminated by

the constraint of chemical equilibrium [e.g., r =

rc( p,

T)]. This leaves two de-

grees of freedommthe same number as for a homogeneous single-component

system. Thus, under saturated conditions, a state variable can be specified as

0 = O(p, T).

5.3.1 Unsaturated Behavior

Under unsaturated conditions, thermodynamic processes for moist air occur

much as they would for dry air because thermal properties are modified only

slightly by the trace abundance of vapor. A change of temperature leads to

124 5

Transformations of Moist

Air

changes of internal energy and enthalpy given by (2.18), but with slightly mod-

ified specific heats (5.12). The saturation mixing ratio r c, which measures the

capacity of air to support vapor in solution, varies with the system's pressure

and temperature. By contrast, the mixing ratio r of vapor actually present

remains constant so long as the system is unsaturated.

The same is approximately true of the potential temperature. Under adia-

batic conditions, pressure and virtual temperature change in such proportion

to preserve the virtual potential temperature

To (5.14)

where Kd denotes the value for dry air. Like virtual temperature, Ov is nearly

identical to its counterpart for dry air, 0. Therefore, virtual properties of moist

air like T v and 0~ will hereafter be referred to by their counterparts for dry

air, but the former will be understood to apply in a strict sense.

5.3.2 Saturated Behavior

Under saturated conditions (e.g., in the presence of an aerosol of droplets),

the aforementioned relationships no longer hold. Because the vapor must then

be at equilibrium with a condensed phase, e = ec. A change of thermodynamic

state that alters ec then also alters e, which must result in a transformation of

mass from one phase of the water component to another. Accompanying that

transformation of mass is an exchange of latent heat between the condensed

and gas phases of the heterogeneous system (Fig. 5.2), one that alters the

potential temperature of the gas phase through (2.36).

State variables describing the two-component heterogeneous system must

account for these changes. For a closed system, (4.7) gives the change of total

enthalpy

~H dT + dp + (ho - hc)dmo. (5.15)

dH = ~

pm Tm

Because

H = mdh d + mvh v + mch c,

- ma \

dT ,I

+ m~ \ dT +

--~ pm pm pm

\OT

Similarly,

= mdCpd -1- mvCpv + mcCpc.

= m d + m v W m c

-~P Tm ~ Tm \--~P,]Tm -~P

(5.16)

For the gas phase,

5.3 State

Variables of the Two-Component System

125

dp ,J Tm k Op Tm

by (2.18). For the condensed phase, the corresponding change of enthalpy can

be expressed

0 c)

Tm - vc(1- TOtp)'

where

ffp ~ --

V p

defines the isobaric expansion coefficient (e.g., Denbigh, 1971). Because C~p is

small for condensed phases,

- PJ m

The contribution to (5.15) from this pressure term can be shown to be neg-

ligible compared to the corresponding contribution from temperature (5.16).

Incorporating the above into (5.15) and identifying the specific heat of the

heterogeneous system as

mdCpd -Jr- mvCpv n t- mcCpc

(5.17)

Cp --

and the latent heat as the difference of enthalpy between the phases of water

l= h~- hc, (5.18)

obtains the change of enthalpy for the system:

dh = cpdT + l dmv

-~ cpdT + ldr. (5.19)

The last expression holds exactly if the specific enthalpy refers to a unit mass

of dry air, derivation of which is left as an exercise. In (5.19), the term

6q - -ldr

represents the heat transferred to the gas phase (which is chiefly dry air) from

the water component when the latter undergoes a transformation of phase.

If l is treated as constant (Sec. 4.6.1), (5.19) may be integrated to yield an

expression for the absolute enthalpy of the two-component heterogeneous

system:

h = cpT + lr + ho, (5.20)

where h0 denotes the enthalpy at a suitably-defined reference state.

126

Transformations of Moist

Air

Expressions for the internal energy and entropy of the system follow in

similar fashion:

u = cvT + lr +

u0, (5.21)

s lr s o

lnT- Kdlnp + ~ -t-

~Cp

lr s o

= In 0 + + --. (5.22)

Cp T Cp

Like (5.19), the expressions for absolute enthalpy, internal energy, and entropy

of the two-component system are exact if referenced to a unit mass of dry air.

5.4 Thermodynamic Behavior Accompanying Vertical Motion

The thermodynamic state of a moist air parcel changes through vertical mo-

tion. Vertical displacement alters the environmental pressure, which varies

hydrostatically according to (1.17). To preserve mechanical equilibrium, the

parcel expands or contracts, which results in work being performed. Compen-

sating that work is a change of internal energy, which alters the temperature

and hence the saturation vapor pressure of the two-component system.

5.4.1 Condensation and the Release of Latent Heat

From (4.38), the change of saturation vapor pressure between a reference

temperature T O and a temperature T can be expressed

ln(ecC0 ) =

Rvl

(1T T01)" (5.23)

Then (5.7) implies that the saturation mixing ratio varies with pressure and

temperature as

exp [-~ (1_ ~)]

rco ( ot

(5.24)

According to (5.24), the saturation mixing ratio increases with decreasing

pressure. However,

r c

decreases sharply with decreasing temperature, which

likewise accompanies upward motion. Therefore, even though an ascending

parcel's pressure decreases exponentially with altitude, the temperature de-

pendence in (5.24) prevails, so its saturation mixing ratio decreases monoton-

ically with altitude.

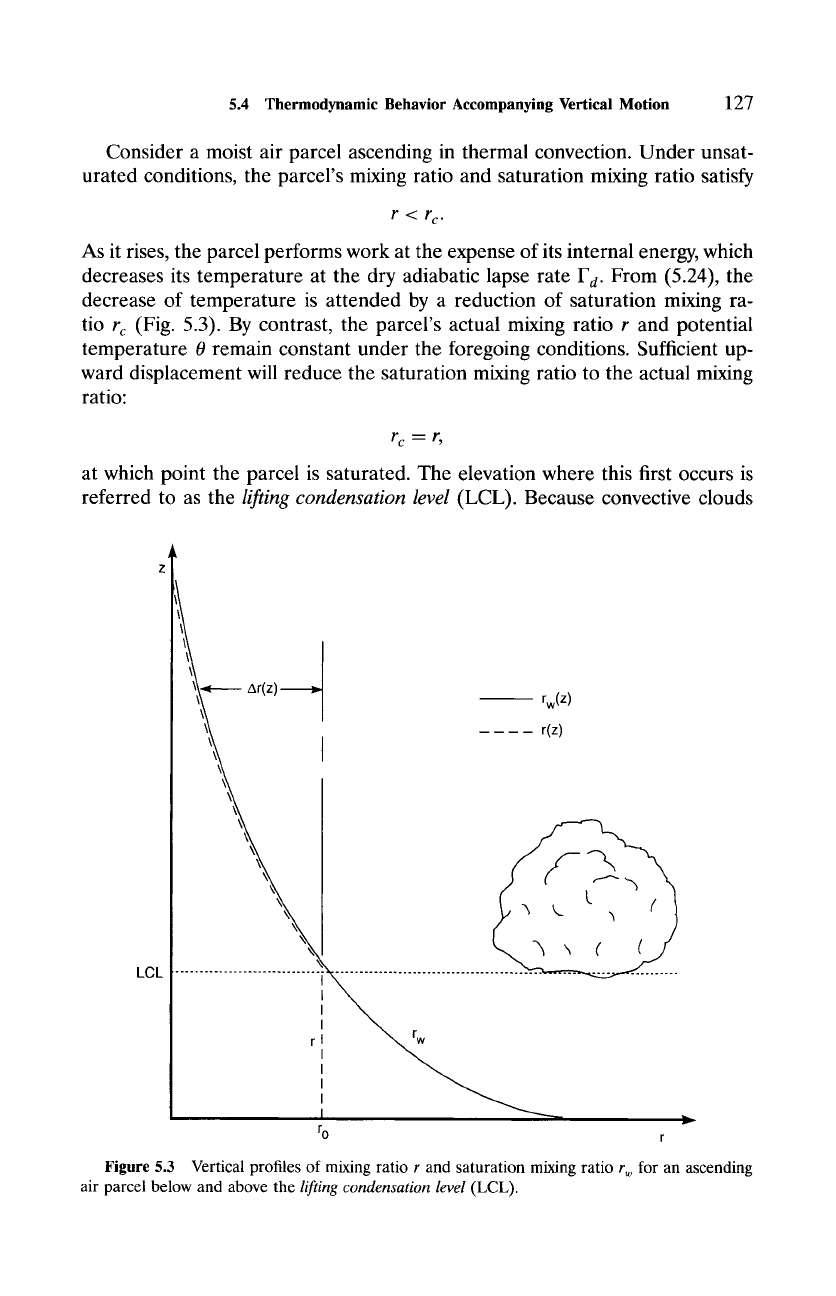
5.4 Thermodynamic Behavior Accompanying Vertical Motion

127

Consider a moist air parcel ascending in thermal convection. Under unsat-

urated conditions, the parcel's mixing ratio and saturation mixing ratio satisfy

r< r c.

As it rises, the parcel performs work at the expense of its internal energy, which

decreases its temperature at the dry adiabatic lapse rate F d. From (5.24), the

decrease of temperature is attended by a reduction of saturation mixing ra-

tio

r c

(Fig. 5.3). By contrast, the parcel's actual mixing ratio r and potential

temperature 0 remain constant under the foregoing conditions. Sufficient up-

ward displacement will reduce the saturation mixing ratio to the actual mixing

ratio:

rc m r,

at which point the parcel is saturated. The elevation where this first occurs is

referred to as the

lifting condensation level

(LCL). Because convective clouds

LCL

\\= Ar(z) -------~ ()

\~ r w z

l r(z)

......................

r o

Figure

5.3 Vertical profiles of mixing ratio r and saturation mixing ratio r w for an ascending

air parcel below and above the

lifting condensation level

(LCL).

128

Transformations of Moist

Air

form through the process just described, the LCL defines the base of cumulus

clouds that are fueled by air originating at the surface.

Below the LCL, the parcel's thermodynamic behavior can be regarded as

adiabatic because the characteristic timescale for vertical displacement (e.g.,

from minutes in cumulus convection to 1 day in sloping convection) is small

compared to the characteristic timescale for heat transfer. Therefore, the par-

cel evolves in state space along a dry adiabat, which is described by Poisson's

equations (2.30) and characterized by a constant value of 0.

In physical space, the parcel is actually part of a layer that is displaced verti-

cally (Fig. 5.4).

Material contours,

which define a fixed collection of fluid elements,

buckle to form a plume of moist air that rises through positive buoyancy. Folds

LCL

Material Contour

(ee= const)

e = const

Figure 5.4 An ascending plume of moist air that develops from surface air that has become

positively buoyant. Material lines (solid), which are defined by a fixed collection of air parcels,

remain coincident with isentropes (0=const) below the LCL, but they drift to higher 0 and higher

altitude above the LCL, where air warms through latent heat release. Although they depart from

isentropes, material lines remain coincident with pseudo-isentropes (0e = const) above the LCL.

5.4

Thermodynamic Behavior Accompanying Vertical Motion

129

in the wall of the plume reflect turbulent entrainment with surrounding air,

which dilutes the plume's buoyancy with that of the environment. Associated

mixing introduces diabatic effects that are ignored in the present analysis, but

play an essential role in dissipating cumulus convection (Chapter 9). Under

unsaturated adiabatic conditions, 0 and r are both conserved for individual

fluid elements. Therefore, a material line that coincides initially with a cer-

tain isentrope 0 = 00 and mixing ratio contour r = r 0 remains coincident with

those isopleths~as long as they reside beneath the LCL.

Above the LCL, the foregoing behavior breaks down. Continued ascent and

expansion work reduces the saturation mixing ratio

r c

below the mixing ratio

r of vapor present. To restore chemical equilibrium, some of the vapor must

condense~just enough to maintain saturation:

r--r c.

Thus, above the LCL, r and

r c

both decrease with height (Fig. 5.3), the de-

crease of vapor being reflected in an increase of condensate (4.6.2).

In this fashion, ascent above the LCL wrings vapor out of solution with

dry air and produces condensate (e.g., cloud droplets). The production of

condensate is attended by a release of latent heat to the gas phase of the

system. Internal to the parcel, that heating alters the potential temperature

of the gas phase through (2.36) and adds positive buoyancy, which in turn

promotes continued ascent. The change of water vapor mixing ratio that results

from a displacement Az above the LCL is given by

Ar(z) :

- ro,

where z, p, and T are understood to refer to the displaced parcel. Because

r c

decreases monotonically with altitude, the greater the displacement above the

LCL, the less vapor that remains in the gas phase of the parcel and the greater

the abundance of condensate and the liberation of latent heat. Cloud droplets

produced in this fashion grow (through mechanisms described in Chapter 9)

until they can no longer be supported by the updraft, at which point they

precipitate out of the parcel.

Since 0 and r are no longer conserved, the material contour coincident initial-

ly with the isopleths 0 = 00 and r = r0 deviates from those isopleths (Fig. 5.4).

The release of latent heat increases 0 (2.36), so the material contour advances to

isentropes of greater potential temperature. For reasons developed in Chap-

ter 7, these lie at a higher altitude than the original isentrope. Similarly, con-

densation reduces r, so the material line moves to isopleths of smaller mixing

ratio, which likewise lie at higher altitude.

Saturated air that is descending undergoes just the reverse behavior. Adia-

batic compression then increases the internal energy and temperature of the

gas phase, which increases the saturation mixing ratio

r c

over the actual mix-

ing ratio r. Condensate can then evaporate to restore chemical equilibrium:

r = r c.

Evaporation of condensate must be attended by absorption of latent