Саградов В.А, Ионцев А.А. Введение в демографию

Подождите немного. Документ загружается.

403

РАЗДЕЛ VI.

ВОСПРОИЗВОДСТВО НАСЕЛЕНИЯ

ГЛАВА 16

РОСТ НАСЕЛЕНИЯ

16.1. КОМПОНЕНТЫ ДЕМОГРАФИЧЕСКОГО РОСТА

Численность жителей Земли непрерывно изменяется в результате процесса

воспроизводства населения. Рождения детей и действие сил смерти, которым

в разной степени подвержены люди всех возрастов, постоянно обновляют

население нашей планеты. Разница между числом рождений и числом смер-

тей называется

естественным приростом населения. Если речь идет

о стране или населенном пункте, то численность их жителей зависит также и

от миграции, точнее, от складывающегося соотношения между прибываю-

щими иммигрантами и их vis-à-vis — эмигрантами. Разница между количе-

ством иммигрантов и эмигрантов называется

миграционным приростом на-

селения. Таким образом, демографический рост является результатом

взаимодействия четырех компонент — рождений, смертей, иммиграции,

эмиграции. Знание закономерностей изменения каждой из названных компо-

нент позволяет решить одну из главных задач демографии — объяснить тен-

денции и оценить перспективы изменения численности населения.

Вставка 16.1. В течение большей части своей истории численность населения

Земли изменялась крайне медленно. Периоды экономического процветания и

роста населения чередовались с социальными и демографическими кризисами,

вызванными войнами, голодом, эпидемиями и природными катаклизмами. Со-

гласно существующим оценкам, на Земном шаре в начале нашей эры проживало

примерно 300 миллионов человек. Потребовалось более 1600 лет, чтобы эта чис-

ленность удвоилась. Быстрый рост мирового населения — сравнительно недав-

ний феномен. Он начался в конце XVIII века и явился отражением набиравшего

темпы процесса демографического перехода. В начале XIX в. численность насе-

ления планеты превысила отметку один миллиард. Уже через сто лет, примерно

в 1927 г. мировое население достигло отметки два миллиарда. В последующие

годы демографический взрыв, произошедший в странах Азии, Африки и Латин-

ской Америки, резко ускорил темпы роста населения мира. Для прибавления

следующего миллиарда жителей Земли потребовалось чуть более 30 лет:

в 1960 г. было отмечено появление трехмиллиардного жителя земли. Через че-

тырнадцать лет, в 1974 г. на Земном шаре уже проживало четыре миллиарда жи-

телей, а еще через тринадцать, в 1987 г. их насчитывалось пять миллиардов.

Достижение мировым населением отметки в шесть миллиардов человек было

отмечено мировой общественностью через двенадцать лет в 1999 г.

404

16.2. УРАВНЕНИЕ ДЕМОГРАФИЧЕСКОГО БАЛАНСА

Если известны числа рождений и смертей, а также миграционный прирост

или его составляющие, то изменение численности населения страны

за определенный период времени вколичественно выражается

уравнением

демографического баланса

или основным демографическим уравнением:

)},0(),0({)},0(),0({)0()( tEtItNtNPtP

−

+= , (16.1),

где

)0(P

)(tP

— численности населения в начале и конце исследуемого

периода;

),( toN

— число родившихся за период

),0( t

;

),( toM

— число

умерших за период

),0( t ; ),( toI — число иммигрантов за период ),0( t ;

),( toE — число эмигрантов за период ),0( t .

То же уравнение можно записать в более обобщенной форме.

Его составляющими будут, с одной стороны,

общий прирост населения,

равный разности между численностями населения на конец

)(tP

и нача-

ло

)0(P

исследуемого периода, а с другой — естественный и миграцион-

ный приросты

, заключенные в фигурных скобках уравнения (16.1):

.. migrnat

∆

, (16.2)

где

)0()( PtPP −=∆ — общий прирост населения;

),0(),0(

tMtNP

nat

−=∆ — естественный прирост; ),0(),0(

tEtIP

migr

−=∆

— миграционный прирост.

16.3. СООТНОШЕНИЕ ЕСТЕСТВЕННОГО И МИГРАЦИОННОГО

ПРИРОСТОВ

В зависимости от соотношений между естественным и миграционным при-

ростом общий прирост населения может принимать как положительные,

так и отрицательные значения. При этом во многих странах и регионах ми-

ра, например, в Китае, Индии или Японии, изменение численности населе-

ния определялось и определяется преимущественно естественным прирос-

том. В то же время в целом ряде стран миграционный прирост оказывал

или оказывает на динамику численности населения не меньшее, а даже

большее влияние по сравнению с естественным приростом. Классическим

примером являются страны Нового света в ХIХ — первой половине

ХХ вв., в которых численность населения увеличивалась в первую очередь

благодоря огромному притоку мигрантов.

Особенности эволюции рождаемости и смертности в регионах мира,

процесс глобализации мирохозяйственных связей привели к тому, что

к концу XX столетия роль миграции в динамике численности населения

возросла (см. табл. 16.1). В 1950-х гг. вклад миграции в демографический

405

рост был особенно значимым в образовавшемся в 1947 г. государстве Из-

раиле и начинавшим разрабатывать свои нефтяные залежи Кувейте,

в прежних британских владениях — Австралии и Канаде, а также центрах

колониальных империй — Великобритании и Португалии. В начале

1990-х гг. доля миграционного прироста в общем приросте населения была

особенно значительной в Германии, Португалии, Израиле и Кувейте, суще-

ственным — в Испании, Нидерландах, Австралии, США, Канаде. В Россий-

ской Федерации значительный приток мигрантов в этот период почти пол-

ностью компенсировал естественную убыль населения.

Табл. 16.1 Отношение миграционного прироста к естественному приросту

в некоторых странах мира в 1950-1955 и 1990-1995 гг. (по абс. величине, в %)

Страны 1950-1955 1990-1995

Израиль 151,3 127,6

Австралия 66,1 50,8

Португалия

61,0

320,0

Кувейт 50,0

314,3

Великобритания

45,1

10,6

Канада 42,9 58,6

Новая Зеландия 39,4 33,3

Алжир

23,2

1,4

Кот Д’Ивуар 18,7 23,3

Испания

17,6

82,1

Нидерланды

16,4

76,7

Германия 16,4

432,8

Филиппины

12,4

11,3

Франция 11,9 37,8

Турция 10,7 0,0

Россия 9,4

110,4

США 9,1 48,5

Пакистан 6,6

11,5

Мексика

4,8

16,8

Индия 4,4

0,5

ЮАР 1,2 0,2

Китай 0,2

1,2

Япония

0,2

0,0

Рассчитано по: World Population Prospects. The 1998 Revision. Volume 1: Com-

prehensive Tables (United Nations, New York, 1999).

Примечание: (-) — в стране отрицательный естественный прирост, (*) —

в стране отрицательный миграционный прирост. Во всех остальных случаях

естественный и миграционный приросты положительны.

406

Роль миграционного прироста в динамике численности населения бу-

дет прослеживаться в еще большей степени, если мы перейдем к исследо-

ванию политико-административных образований с прозрачными для внеш-

него мира границами, таких как провинции стран или отдельные

населенные пункты.

16.4. ПРИМЕНЕНИЕ УРАВНЕНИЯ ДЕМОГРАФИЧЕСКОГО БАЛАНСА

На основе уравнения демографического баланса оценивается численность

населения в межпереписные годы и годы, следующие за последней перепи-

сью населения. Таким образом, например, получены оценки численности

населения России после «переписного» 1989 г. С помощью этого уравнения

определяется величина ошибок в учете естественного и миграционного

движения населения, которые наблюдаются даже в развитых странах с на-

лаженным статистическим учетом населения. Ошибка, получающаяся

при сведении левой и правой частей демографического баланса, называется

«ошибкой закрытия баланса». Как правило, эта ошибка связана

с неполнотой текущего учета миграции.

Во многих странах и отдельных административных образованиях (про-

винции, города) нельзя построить уравнение баланса с учетом всех компо-

нент демографического роста из-за крайне плохой регистрации мигрантов

или ее полного отсутствия. В таком случае знание общего и естественного

приростов за межпереписной период позволяет оценить примерную величи-

ну миграционного прироста населения в этих странах, городах и т.д.

(см. раздел «Миграционное движение и урбанизация».)

Вставка 16.2. В табл. 16.2 приведен демографический баланс России за 1980–

1989 гг., построенный по данным Госкомстата России. Ошибка закрытия баланса,

равняется 383 тысячи человек. С учетом этой поправки миграционный прирост за

указанный период составил не 1354, а 1737 тысяч человек.

Табл. 16.2. Демографический баланс населения России за 1980–1989 гг. (тыс. чел.)

численность населения

на 1 января

количество событий

за 1980-1989 гг.

1980 г.

138291

1 Родившихся

21365

1989 г.

147400

2 Умерших

13993

3 Ест. прирост = (1) – (2)

7372

4 Прибывших

8034

III

общий прирост

населения за 1980–

1989 гг. = II–I

9109

5 Выбывших

6680

6 Мигр. прирост = (4) – (5)

1354

7 Общий прирост = (3) + (7)

8726

Ошибка закрытия

баланса

= (III) – (7)

383

Рассчитано по: «Демографический ежегодник России 1997». М.: Госкомстат, 1998.

407

16.5. КОЭФФИЦИЕНТ ОБЩЕГО ПРИРОСТА НАСЕЛЕНИЯ

Уравнение демографического баланса может быть выражено через общие

коэффициенты миграционного и естественного приростов, рождаемости,

смертности, прибытий и выбытий. Для этого надо правую и левую части

уравнения демографического баланса разделить на среднюю численность

населения страны за период

),0( t и длину периода

. В левой части нового

уравнения будет стоять коэффициент общего прироста населения, который

представляет собой отношение общего прироста населения к его средней

численности за исследуемый период, умноженной на длину этого периода:

.. migrnat

KKK

∆∆

∆

, (16.3)

где

∆

— коэффициент общего прироста населения;

.nat

∆

— коэффи-

циент естественного прироста;

.migr

∆

— коэффициент миграционного

прироста.

Иначе, коэффициент общего прироста населения записывается в виде:

−

∆

imnK

где

,,, imn

— соответственно общие коэффициенты рождаемости, смерт-

ности, иммиграции и эмиграции.

Коэффициент общего прироста является мерой скорости роста попу-

ляции. Подобно всем общим демографическим коэффициентам его вели-

чина зависит от возрастно-половой структуры населения.

16.6. ОТКРЫТОЕ И ЗАКРЫТОЕ НАСЕЛЕНИЯ

Население, у которого отсутствует миграционный обмен с внешним миром,

т.е. количество эмигрантов и иммигрантов равно 0, называется

закрытым.

Демографический рост в данном случае полностью определяется естествен-

ным приростом населения. Принцип «закрытого населения», введенный в

демографию Леонардом Эйлером в XVIII веке

, используется в классических

моделях воспроизводства населения (см. главы 17, 18). С их помощью изу-

чаются нетривиальные взаимосвязи между процессами рождаемости, смерт-

ности, изменением численности и половозрастного состава населения

без учета миграции.

Реальное население можно считать закрытым, если в нем миграцион-

ный обмен с другими странами отсутствует или является крайне незначи-

тельным. Примером абсолютно закрытого населения является все населе-

Opera omnia, ser. 1. / Opera mathematica, Vol. 7, Lpz., 1923. См. также Работу Паев-

ского В.В. Демографические работы Л. Эйлера // В кн. Л. Эйлер. М.–Л., 1935.

408

ние Земного шара, демографический баланс которого представлен

во вставке 16.3. Другие примеры закрытого населения можно найти среди

исторических популяций, которые часто в силу природных обстоятельств

были изолированы от других стран и народов. В современном мире прак-

тически нет государств, у которых миграционные контакты с внешним ми-

ром сведены к нулю (исключительный пример — Северная Корея).

Вставка 16.3. Демографический баланс Земного шара в 1995–2000 гг.

общий прирост населения родившиеся – умершие

395 миллионов 659 миллионов – 264 миллиона

в виде общих коэффициентов баланс выглядит следующим образом:

13,5‰ 22,5‰ – 9,0‰

Источник: World Population Prospects. The 2000 Revision. Volume 1: Compre-

hensive Tables. United Nations, New York, 2000.

Соответственно, мы говорим об открытом населении в том случае,

когда границы территории его проживания оказываются прозрачными

для мигрантов. Следует отметить, что равенство миграционного прироста

нулю не означает, что перед нами закрытое население. Нулевой миграци-

онный прирост может быть результатом совпадения объемов эмиграцион-

ного оттока и иммиграционного притока. Различия в структурах (возрас-

тная, половая и другие) этих противонаправленных потоков изменяют

соответствующие структуры всего населения.

16.7. КОЭФФИЦИЕНТЫ РОСТА И ПРИРОСТА НАСЕЛЕНИЯ

Для характеристики скорости изменения демографического роста

во времени используются традиционные статистические характеристики

рядов динамики —

темп роста и темп прироста. Темп роста показывает

во сколько раз увеличилось население за временной период. Он равен от-

ношению численности населения в последующий момент времени

к численности населения в момент, ему предшествующий:

)0(

)1(

=θ , (16.4)

где

θ — темп роста населения за период )1,0( ; )1(P — численность на-

селения в конечный момент времени;

)0(P — численность населения в на-

чальный момент времени.

При увеличении численности населения отношение (4) будет больше 1

(или 100, если темп роста выражается в процентах), при сокращении —

наоборот, меньше 1 (или 100%).

Темп прироста населения рассчитывается как отношение величины

общего прироста населения к численности населения на начало исследуе-

409

мого периода или как разность между темпом роста и 1 (или 100%, если

темп роста рассчитывается в процентах):

)0(

)1(

)0(

)0()1(

−θ=−=

−

=θ

рпp

. (16.5)

Темп прироста показывает, на сколько процентов увеличилась или со-

кратилась численность населения за исследуемый период времени. Если

его величина имеет положительный знак, то численность население растет,

если отрицательный — убывает.

В странах с налаженным учетом населения темпы роста и прироста

населения можно рассчитать за каждый год. Однако в большинстве случаев

эти показатели оцениваются за межпереписные или пятилетние временные

периоды. Поскольку межпереписные периоды в одной и той же стране, а

также в разных странах могут иметь разную протяженность, то для кор-

ректного сравнения исчисляются среднегодовые темпы прироста и роста

населения (см. параграф 16.9 б).

Темп прироста, подобно коэффициенту общего прироста населения, яв-

ляется мерой скорости изменения численности населения. Но эти показатели

отличаются друг от друга по величине, поскольку в одном случае знамена-

тель равен среднему населению, в другом — численности населения в начале

исследовательского интервала. Как правило, различия между показателями,

особенно для однолетних и менее продолжительных временных интервалов,

невелики из-за сравнительно невысоких темпов роста, свойственных челове-

ческим популяциям. Наибольшая разница между показателями наблюдается

в тех популяциях, численность которых изменяется очень быстро.

16.8. ПРОСТЫЕ МОДЕЛИ ДЕМОГРАФИЧЕСКОГО РОСТА

Простыми

называют демографические модели, в которых с помощью из-

вестных аналитических функций (линейные, экспоненциальные, гипербо-

лические и др.) описывается динамика численности населения без учета

изменений возрастно-половой структуры и его других внутренних характе-

ристик. Простые модели демографического роста населения появились

в демографической науке в XVII веке. В дальнейшем их использовали

в своих теоретических исследованиях выдающиеся математики и демогра-

фы Л. Эйлер, В. Борткевич и А. Лотка.

В настоящее время простые модели

роста населения применяются для решения самых разнообразных демогра-

фических и экономических задач, в частности:

– для выполнения интерполяционных, ретроспективных и прогнозных

оценок численности всего населения и его отдельных групп;

В зарубежной научной литературе такие модели иногда называют примитивными

демографическими моделями.

410

– для оценки демографической ситуации, на них основаны некоторые

демографические показатели;

– в качестве экзогенных предпосылок они входят в различные эконо-

мические модели.

16.9. ДЕМОГРАФИЧЕСКИЙ РОСТ С ПОСТОЯННЫМ

ТЕМПОМ ПРИРОСТА

а) изменение населения по закону геометрической прогрессии

Пусть нам известна численность некоторого населения на начало го-

да

)0(P и темп его прироста за год

пр

. Численность этого населения

на конец текущего (или начало следующего) года можно определить

по формуле (16.6):

)1()0()1(

пр

PP θ+⋅=

. (16.6)

Если темп прироста останется в будущем неизменным, то можно опре-

делить численность населения в течение всех последующих лет. Общая схе-

ма изменения численности населения будет выглядеть следующим образом:

численность

населения на:

правило вычисления

начало первого года

)0(P

конец второго года

)1()0()1(

пр

⋅

конец третьего года

)1()0()1()1()2(

прпр

PPP θ+⋅=θ+⋅=

конец четвертого года

)1()0()1()1()1()2()3(

прпрпр

PPPP θ+⋅=θ+⋅=θ+⋅=

… …

конец года τ

θ+⋅==θ+⋅−τ=τ )1()0()1()1()(

прпр

PPP …

Из последнего выражения следует, что на протяжении

лет числен-

ность исследуемого населения на конец каждого

k–го года будет изменять-

ся по формуле

пр

PkP )1()0()( θ+⋅= , (16.7)

т.е.

по закону геометрической прогрессии. Таким образом, геометрическая

прогрессия является моделью изменения численности населения

с постоянным годовым темпом прироста.

б) экспоненциальный демографический рост

По закону геометрической прогрессии численность населения меняет-

ся дискретно, т.е. в определенной точке временного промежутка (в нашем

411

случае — в конце каждого года). Однако в реальной действительности чис-

ленность населения изменяется непрерывно, т.е. в каждой точке временно-

го интервала. Поэтому аналитическое описание демографического роста

с помощью непрерывных процессов более адекватно, чем на основе дис-

кретных. Непрерывным аналогом геометрической прогрессии является

экспоненциальная функция. Таким образом, формула непрерывного демо-

графического роста выражается уравнением

ePkP

⋅

⋅= )0()( , (16.8)

где

e — основание натурального логарифма ( 718281828,2

≈

e );

— моме-

нтальный коэффициент прироста населения, являющийся постоянной. Если

величина

больше нуля, то численность населения увеличивается, если

меньше нуля —уменьшается, если

равно 0 — остается постоянной.

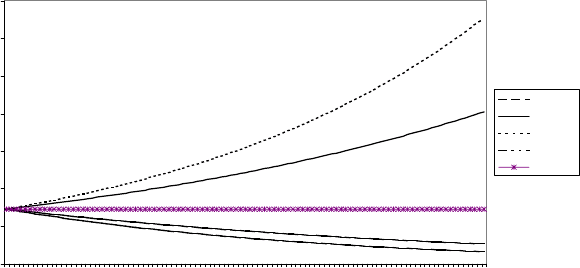
Пример кривых экспоненциального роста при разных значениях постоян-

ной

можно увидеть на рисунке 16.1.

100

200

300

400

500

600

700

2000

2004

2008

2012

2016

2020

2024

2028

2032

2036

2040

2044

2048

2052

2056

2060

2064

2068

2072

2076

2080

2084

2088

2092

2096

2100

r=-1%

r=1%

r=1,5%

r=-1,5%

r=0

Рис. 16.1. Модель экспоненциального роста населения России

в 2000–2100 гг. при разных параметрах

(в млн. чел.)

Однако практика показала, что все гипотезы о динамике численности

населения, основанные на экспоненциальной модели, не выдерживали про-

верки практикой на длительных периодах. Темпы демографического роста

меняются. Кроме того, на них влияет демографический потенциал, накоп-

ленный возрастной структурой. Применение возможностей модели

для выполнения ретроспективных и перспективных оценкок демографиче-

ской динамики ограничено короткими временными интервалами.

б) среднегодовые темпы прироста населения

Для сравнения скорости увеличения численности населения в разные

по продолжительности периоды необходимо оценивать среднегодовые

412

темпы роста и прироста населения. В основе этих оценок лежат предполо-

жения о том, что в изучаемый межпереписной период население изменя-

лось по геометрической прогрессии или экспоненциальному закону.

Из формулы (16.7) путем простых арифметических преобразований непо-

средственно определяется неизвестная величина

пр

, которая и является

среднегодовым темпом прироста населения за

k лет:

)0(

)(

−=θ

пр

, (16.9)

Если единицу перенести в правую часть уравнения, то мы получим

среднегодовой темп роста населения:

прр

)0(

)(

1 =θ+=θ

Пусть теперь население изменяется по экспоненциальному закону. Тогда

из уравнения (16.8) среднегодовой темп прироста населения за

k лет равен:

PkP

)0(/)(ln(

. (16.9)

16.10. ПЕРИОД УДВОЕНИЯ ЧИСЛЕННОСТИ НАСЕЛЕНИЯ

Один из самых распространенных подходов к оценке современной демо-

графической ситуации заключается в оценке настоящего через будущее.

Мы предполагаем, что параметры «сегодняшнего дня» у населения сохра-

нятся и в отдаленной перспективе. Затем анализируются демографические

характеристики, которые население приобретет в будущем. Одним из таких

показателей, оценивающих настоящее через будущее, является «период

удвоения численности населения». Он измеряет скорость демографическо-

го роста временем, которое потребуется некоторому населению, чтобы уд-

воить свою численность при сохранении данного темпа прироста.

Чем короче этот период, тем быстрее растет население. Естественно, если

прирост населения имеет отрицательную величину, то речь идет о времени

двукратного сокращения численности населения.

Период удвоения легко рассчитать как для дискретного, так и непре-

рывного времени демографических изменений. В первом случае из форму-

лы геометрической прогрессии при условии

)0(2)( PTP

⋅

следует

пр

PP )1()0()0(2 θ+⋅=⋅ . Откуда получаем, что период удвоения равен:

)1ln(

2ln

пр

θ+

= . (16.11)