Русаков В.С. и др. Механика. Методика решения задач

Глава 7. Законы сохранения момента импульса и механической энергии

231

ГЛАВА 7

ЗАКОНЫ СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА И

МЕХАНИЧЕСКОЙ ЭНЕРГИИ. ГИРОСКОПЫ.

ГИРОСКОПИЧЕСКИЕ СИЛЫ

7.1. Теоретический материал

Закон сохранения момента импульса (количества движе-

ния) механической системы относительно точки

1

– момент им-

пульса механической системы

L относительно инерциальной сис-

темы отсчета сохраняется, если сумма моментов внешних сил

ex

M

относительно данной точки равна нулю:

0

d

ex

== M

L

t

или 0d

=

L . (7.1)

Закон сохранения момента импульса (количества движе-

ния) механической системы относительно оси

– момент импуль-

са механической системы

n

L относительно инерциальной системы

отсчета сохраняется, если сумма моментов внешних сил

ex

n

M отно-

сительно данной оси равна нулю:

0

d

ex

==

n

M

t

L

или

0d =

n

L . (7.2)

Для конечного интервала времени законы сохранения момен-

тов импульса механической системы относительно точки и оси в

соответствии с (7.1) и (7.2) можно записать в виде:

0)()(Δ

12

=

−

≡

tt LLL или )()(

21

tt LL

=

, (7.3)

0)()(Δ

12

=

−≡ tLtLL

nnn

или

)()(

21

tLtL

nn

=

. (7.4)

Законы сохранения моментов импульса относительно точки

и оси являются прямым следствием законов их изменений (см.

(6.38) и (6.39) в п. 6.1 Теоретический материал в Главе 6).

1

Определения момента импульса (количества движения) механи-

ческой системы и момента силы относительно точки (оси), а также фор-

мулировка закона изменения момента импульса (уравнения моментов)

относительно точки (оси) даны в п. 6.1 Теоретический материал в Главе 6.

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

232

Кинетическая энергия абсолютно твердого тела

2

в случае

его произвольного движения равна:

[]

()

=

′

+==

∑∑

2

2k

2

1

2

1

i

ii

i

ii

mmE rωVυ

[][]

()

=

′

+

′

⋅+=

∑

i

iii

Vm

2

1

rωrωV

[]

∑

′

+

′

⋅+=

i

ii

mmmV

2

цм

2

1

2

1

rωrωV . (7.5)

Здесь m

i

и

i

υ – массы и скорости материальных точек, из которых

состоит абсолютно твердое тело,

V – скорость начала системы от-

счета S', жестко связанной с телом,

ω – угловая скорость системы

S',

i

r

′

– радиус-векторы материальных точек тела относительно

системы S',

цм

r

′

– радиус-вектор центра масс (см. Главу 3) тела от-

носительно системы S'.

Если начало отсчета системы S', связанной с абсолютно

твердым телом, совпадает с центром масс тела, то его кинетическая

энергия равна сумме кинетической энергии поступательного дви-

жения тела со скоростью центра масс и кинетической энергии вра-

щательного движения тела вокруг оси, проходящей

через центр

масс:

[]

∑

′

+=

i

ii

mmE

2

цм

k

2

1

2

1

rωυ

, (7.6)

где

цм

υ – скорость центра масс тела.

Кинетическая энергия вращающегося тела вокруг непод-

вижной оси:

2k

2

1

ω

JE = , (7.7)

где

J – момент инерции тела относительно оси вращения,

ω

– угло-

вая скорость вращения тела.

2

Определение кинетической энергии механической системы даны в

п. 3.1 Теоретический материал в Главе 3, а определение абсолютно твер-

дого тела в п. 6.1 Теоретический материал в Главе 6.

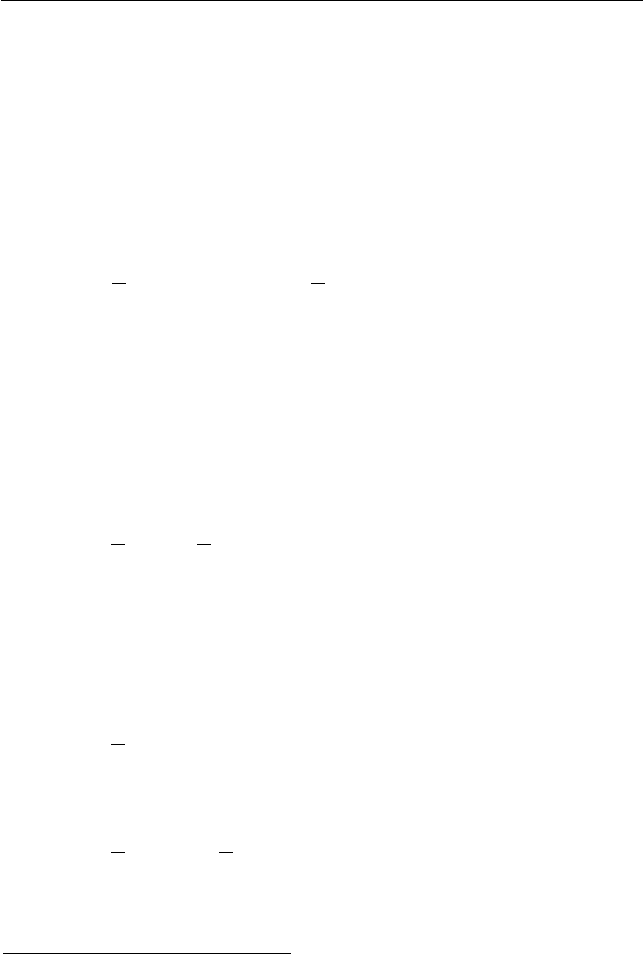
Глава 7. Законы сохранения момента импульса и механической энергии

233

Работа внешних сил при повороте тела вокруг оси:

ϕ

δ

d

n

MA

=

,

∫

=

2

1

d

12

ϕ

n

MA , (7.8)

где

M

n

– момент сил относительно оси (см. п. 6.1 Теоретический

материал в Главе 6),

ϕ

1

и

ϕ

2

– начальное и конечное значения угла

поворота.

Кинетическая энергия абсолютно твердого тела в случае

его плоского движения:

[]

2

цм

2k

2

1

2

1

ω

JmmVE +

′

⋅+= rωV

. (7.9)

Здесь смысл обозначений физических величин тот же, что и в (7.5)

и (7.7).

Если начало отсчета системы S', связанной с абсолютно

твердым телом, находится в центре масс тела, то его кинетическая

энергия равна сумме кинетической энергии поступательного дви-

жения тела со скоростью центра масс и кинетической энергии

вра-

щательного движения тела вокруг оси, проходящей через центр

масс, и в случае плоского движения равна (теорема Кенига):

2

цм

2

цм

k

2

1

2

1

ωυ

JmE += , (7.10)

где

цм

υ

– скорость центра масс тела,

цм

J

– момент инерции тела

относительно оси вращения, проходящей через его центр масс.

Кинетическая энергия абсолютно твердого тела, записан-

ная через

момент инерции тела

n

J относительно мгновенной оси

вращения

3

:

2k

2

1

ω

n

JE = . (7.11)

Кинетическая энергия абсолютно твердого тела, закреп-

ленного в точке:

[]

2

2k

2

1

2

1

∑∑

=≡

i

ii

i

ii

mmE ωrυ , (7.12)

3

Определение мгновенной оси вращения дано в

п. 6.1 Теоретический материал в Главе 6.

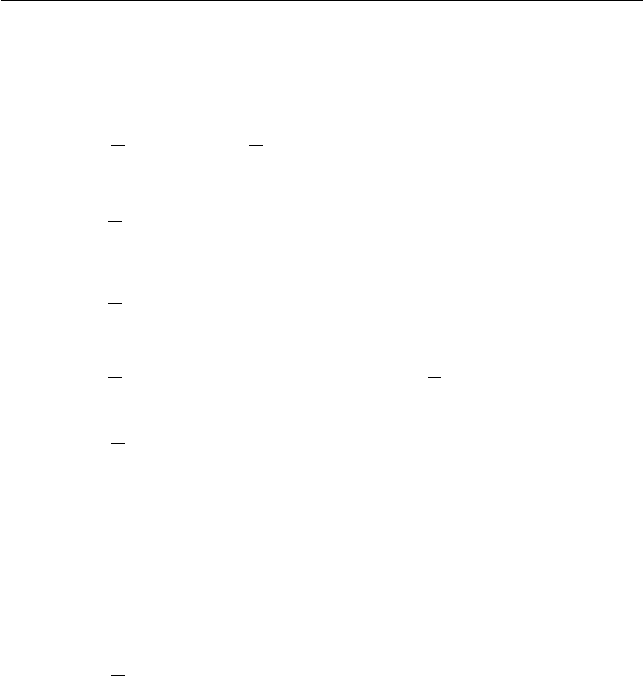
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

234

где

i

r – радиус-векторы материальных точек, из которых состоит

тело, относительно закрепленной точки этого тела. Если восполь-

зоваться математическим соотношением

[

]

(

)

2

22

2

abbaab −= , то:

[]

()

(

)

=−==

∑∑

2

22

2

k

2

1

2

1

ii

i

ii

mmE ωrrωr

ω

=

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−=

∑∑∑

2

22

2

1

α

αα

α

ωω

ii

i

xrm

=

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

=

∑∑∑

βα

ββαα

βα

βααβ

ωωωωδ

,

2

,

2

1

iii

i

xxrm

()

βα

αββα

βα

βααβ

ωωωωδ

∑∑∑

=

⎭

⎬

⎫

⎩

⎨

⎧

−=

,,

2

1

2

1

Jxxrm

iii

i

,

βα

αβ

ωω

∑

=

,

k

2

1

JE .

(7.13)

Здесь

(

)

∑

−=

i

iiii

xxrmJ

βααβαβ

δ

2

– тензор инерции тела, характе-

ризующий распределение массы тела относительно точки;

αβ

δ

–

символ Кронекера.

Кинетическая энергия абсолютно твердого тела закреп-

ленного на оси:

2k

2

1

ω

n

JE = , (7.14)

где

n

J – момент инерции тела относительно оси.

В данной главе рассматриваются системы, состоящие из со-

вокупности абсолютно твердых тел и материальных точек. Эти

системы являются частными случаями механической системы, для

которой в Главе 3 сформулированы законы изменения и сохране-

ния механической энергии.

Закон изменения механической энергии системы – изме-

нение механической энергии системы равно работе внутренних

Глава 7. Законы сохранения момента импульса и механической энергии

235

innp,

i

F и внешних

exnp,

i

F непотенциальных сил

4

:

(

)

npexnp,innp,

d AAAE

δδδ

=+−= , (7.15)

или для конечного интервала времени

np

ΔΔ A

E

=

. (7.16)

Закон сохранения механической энергии системы – если

работа всех непотенциальных сил равна нулю, то механическая

энергия системы относительно инерциальной системы отсчета со-

храняется:

0)()(Δ

12

=

−

≡

tEtEE

или

)()(

21

tEtE = . (7.17)

Гироскопы

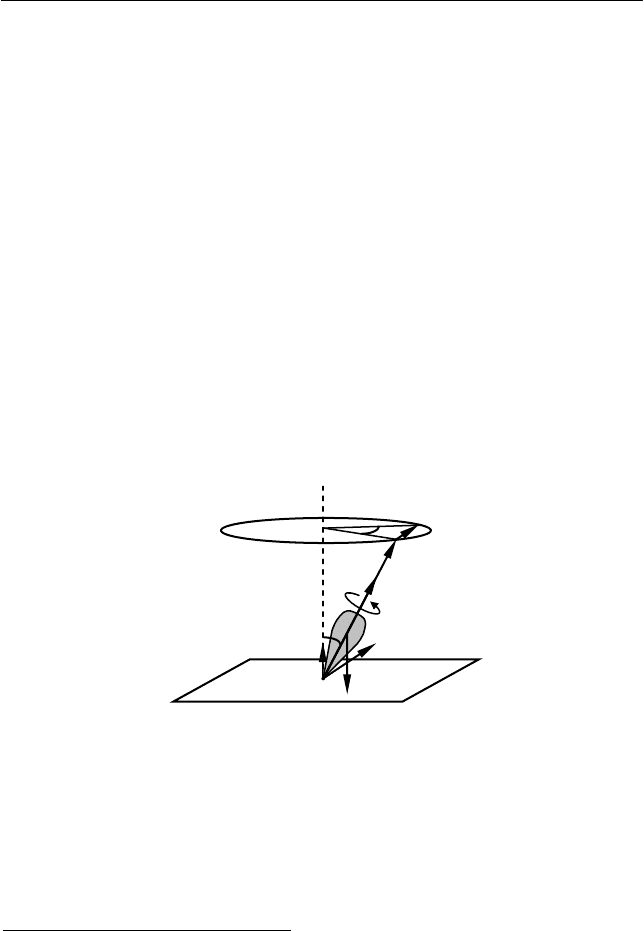
Гироскоп

– это аксиально-симметричное тело, вращающееся

с большой угловой скоростью

ω вокруг своей оси симметрии (см.

рис. 7.1).

Прецессия гироскопа

– вращение оси симметрии гироскопа

с угловой скоростью

Ω под действием момента внешних сил на-

ряду с его собственным вращением вокруг оси симметрии (см.

рис. 7.1).

4

Определение механической энергии системы, внутренних и

внешних непотенциальных сил даны в п. 3.1 Теоретический материал в

Главе 3.

Рис. 7.1. Гироскоп в поле сил тяжести

L

Ld

Ω

tΩd

M

g

m

ω

ϑ

O

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

236

Основные физические допущения элементарной теории ги-

роскопа:

- угловая скорость вращения гироскопа и его момент им-

пульса направлены вдоль оси симметрии гироскопа;

- величина угловой скорости вращения гироскопа вокруг

своей оси

ω гораздо больше величины угловой скорости прецес-

сии

Ω .

В рамках принятых допущений момент импульса гироскопа

L равен

ωL

z

J

=

, (7.18)

а уравнение моментов (6.38) относительно его неподвижной точки

O (см. рис. 7.1) имеет вид:

M

L

=

td

d

,

(7.19)

где

J

z

– момент инерции гироскопа относительно своей оси сим-

метрии,

M – сумма моментов внешних сил (в том числе силы тяже-

сти), действующих на гироскоп.

В соответствии с (7.19) ось гироскопа вместе с моментом

L

прецессирует вокруг вертикального направления с угловой скоро-

стью Ω .

На рис. 7.1 видно, что:

tLL dsind

Ω

ϑ

⋅

=

, (7.20)

[]

tdd ΩLL

=

. (7.21)

Следовательно, прецессия гироскопа описывается уравнени-

ем:

[]

ΩL

L

=

td

d

. (7.22)

С учетом уравнения моментов (7.19) для гироскопа получим:

[] []

ΩωΩLM

z

J=

=

. (7.23)

Заметим, что момент импульса определяет угловую скорость,

а не ускорение прецессии, т.е. прецессионное движение является

безинерционным!

Гироскопические силы – силы, действующие на крепление

(рамку, подшипник, руки экспериментатора и т.д.) несвободного

гироскопа при вынужденном вращении оси (вынужденной прецес-

сии) гироскопа.

Глава 7. Законы сохранения момента импульса и механической энергии

237

В соответствии с третьим законом Ньютона на крепление

действует момент гироскопических сил:

[]

[

]

ΩωΩLMM

z

J

−

=

−=−=

г

. (7.24)

Правило Н.Е. Жуковского – гироскопические силы стре-

мятся совместить момент импульса гироскопа с направлением уг-

ловой скорости вынужденного поворота.

7.2. Основные типы задач и методы их решения

7.2.1. Классификация задач

Большинство задач, относящихся к теме "Законы сохранения

момента импульса и механической энергии. Гироскопы. Гироско-

пические силы" можно условно отнести к следующим типам задач

или их комбинациям. Задачи на

1) законы сохранения момента импульса и механической

энергии системы (в том числе включающей в себя абсолютно твер-

дые тела),

2) гироскопы и гироскопические силы

.

7.2.2. Общая схема решения задач

I.

Определиться с моделями материальных объектов и явле-

ний.

1. Нарисовать чертеж, на котором изобразить рассматривае-

мые тела.

2. Выбрать систему отсчета (из соображений удобства), отно-

сительно которой будут рассматриваться законы сохране-

ния (изменения) механической энергии и момента им-

пульса механической системы, изобразить на чертеже ее

систему координат, а также точку (ось), относительно ко-

торой записываются моменты импульсов и сил.

3. Изобразить и обозначить силы и необходимые кинемати-

ческие характеристики системы.

4. Выбрать механическую систему и рассматриваемый ин-

тервал (начальный и конечный моменты) времени.

5. Выбрать модели тел (если это не сделано в условии задачи)

и рассмотреть особенности их движения на рассматривае-

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

238

мых интервалах времени (непосредственно перед соуда-

рением, сразу после соударения, и т.д.).

6. Провести анализ действующих на тела системы сил и их

моментов относительно выбранной точки (оси) вращения.

II. Записать полную систему уравнений по отношению к иско-

мым величинам.

1. Выбрать законы сохранения (изменения) и записать их в

выбранной системе отсчета для выбранной механической

системы и выбранных интервалов времени в рамках вы-

бранной модели движения тел системы.

2. Записать выражения для моментов сил, моментов инерции

и импульса тел и механической энергии системы тел с

учетом характера их движения.

3. Записать уравнения

кинематической связи.

4. Использовать результаты ранее решенных задач и особые

условия задачи.

III. Получить искомый результат в аналитическом и числен-

ном видах.

1. Решить систему полученных уравнений.

2. Провести анализ решения (проверить размерность и лиш-

ние корни, рассмотреть характерные случаи, установить

область применимости).

3. Получить численный результат.

7.3. Примеры решения задач

7.3.1. Законы сохранения

момента импульса и механической энергии

Задача 7.1

Вокруг горизонтальной оси, проходящей через точку закреп-

ления математического маятника массой m и длиной l, может вра-

щаться без трения однородный стержень массой

M и длиной L ≥ l,

шарнирно закрепленный в той же точке (см. рис. 7.2). Маятник от-

пускают из горизонтального положения. Найти максимальный угол

отклонения стержня

α

max

после абсолютно упругого соударения c

маятником.

Глава 7. Законы сохранения момента импульса и механической энергии

239

Решение

I. Выберем лабораторную инерци-

альную систему отсчета, жестко связан-

ную с точкой подвеса математического

маятника и стержня. Направим горизон-

тальную ось вращения за плоскость чер-

тежа (см. рис. 7.2).

Выберем четыре момента времени:

t

1

– момент начала движения математиче-

ского маятника,

t

2

– момент непосредственно перед соударением

маятника со стержнем,

t

3

– момент сразу после соударения, t

4

– мо-

мент, соответствующий максимальному отклонению стержня. В

течение временного интервала (

t

1

, t

2

) сохраняется механическая

энергия математического маятника. В промежутке времени (

t

2

, t

3

)

сохраняются механическая энергия и момент импульса системы

тел «маятник + стержень». Импульс системы тел в этом промежут-

ке не сохраняется, поскольку в точке подвеса стержня во время со-

ударения возникают дополнительные силы, импульс которых от-

личен от нуля. В промежутке времени (

t

3

, t

4

) сохраняется механиче-

ская энергия стержня вследствие отсутствия сил трения.

Потенциальные энергии математического маятника и стерж-

ня будем считать равными нулю при их вертикальной ориентации.

II. Запишем закон сохранения механической энергии (7.17)

для математического маятника на интервале времени (

t

1

, t

2

):

2

11

ω

J

mgl = . (7.25)

Здесь mgl – потенциальная энергия маятника в его исходном гори-

зонтальном положении (в момент времени t

1

),

2

11

ω

J

– кинетиче-

ская энергия маятника непосредственно перед соударением (в мо-

мент времени t

2

), J

1

– момент инерции маятника относительно оси

вращения,

ω

1

– его угловая скорость перед соударением.

Для временного интервала (t

2

, t

3

) закон сохранения момента

импульса (7.4) и механической энергии (7.17) для системы тел «ма-

ятник + стержень» имеют вид:

312211

ω

JJJ += , (7.26)

Рис. 7.2

l

M, L

/2

π

m

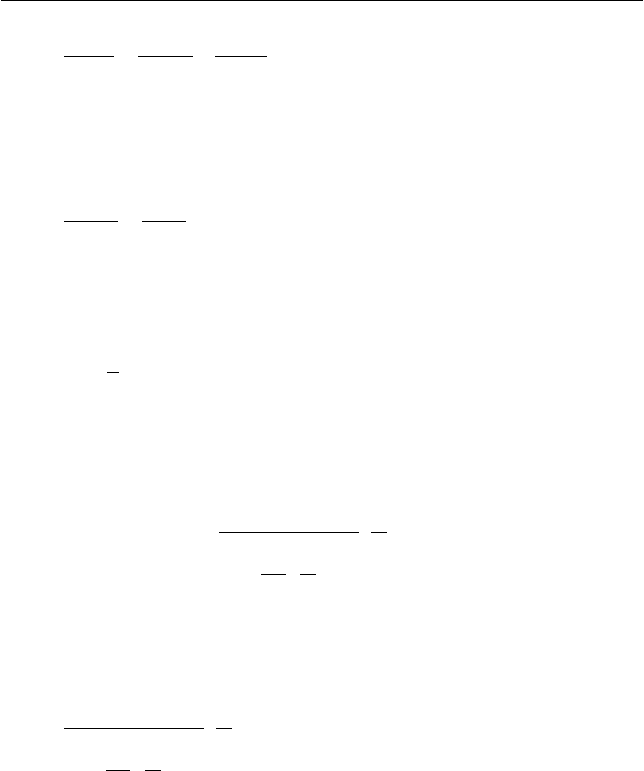
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

240

222

2

31

2

22

2

11

ω

ωω

J

JJ

+= ,

(7.27)

где J

2

– момент инерции стержня,

ω

2

и

ω

3

– угловые скорости вра-

щения стержня и маятника сразу после соударения.

Запишем также закон сохранения механической энергии

(7.17) для стержня на интервале времени (t

3

, t

4

):

()

max

2

22

cos1

22

α

ω

−=

MgLJ

. (7.28)

Моменты инерции маятника

1

J и стержня

2

J относительно

выбранной оси вращения равны:

2

1

mlJ = , (7.29)

2

3

1

MLJ

= . (7.30)

III. Решая систему уравнений (7.25) – (7.30) относительно ис-

комого максимального угла отклонения стержня, получаем:

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+

−=

l

L

l

L

m

M

2

max

3

24

1arccos

α

. (7.32)

Поскольку

max

α

не может превышать

2/

π

, то на соотноше-

ния масс mM / и длин lL / стержня и математического маятника

накладывается условие:

1

3

24

2

<⋅

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+

l

L

l

L

m

M

, (7.33)

при нарушении которого стержень ударится о потолок.

На рис. 7.3 изображены области значений отношений длин и

масс маятника и стержня, при которых максимальный угол откло-

нения стержня в результате соударения с математическим маятни-

ком меньше или равен

2/

π

. Кривая, изображенная на рис. 7.3 со-

ответствует значениям отношений длин Ll /

и масс Mm / маятни-

ка и стержня, при которых стержень принимает горизонтальное

положение, не соударяясь с потолком. Область значений отноше-

Русаков В.С. и др. Механика. Методика решения задач

Подождите немного. Документ загружается.