Русаков В.С. и др. Механика. Методика решения задач

Глава 6. Кинематика и динамика абсолютно твердого тела

211

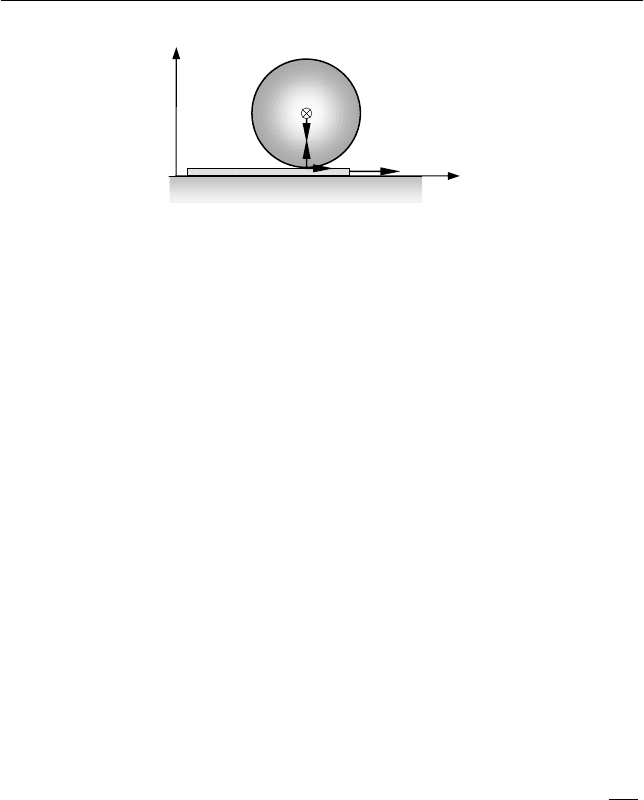
II. Уравнение движения центра масс шара (совпадающего с

его геометрическим центром) в проекциях на оси X и Y лаборатор-

ной системы координат имеют вид:

тр22

Fam = , (6.87)

gmN

2

0 −

=

, (6.88)

где F

тр

– модуль силы трения покоя, действующей на шар со сторо-

ны доски, N – модуль силы нормальной реакции доски, действую-

щей на шар.

Доска движется с ускорением

а

1

в направлении оси X под

действием силы

F и силы трения со стороны шара, модуль которой

в соответствии с третьим законом Ньютона равен модулю F

тр

силы

трения покоя, действующей на шар со стороны доски.

Уравнение движения доски относительно лабораторной

инерциальной системы отсчета в проекции на ось X имеет вид:

тр11

FFam −= . (6.89)

Уравнение моментов (6.47) для шара запишем относительно

оси вращения, проходящей через его центр масс перпендикулярно

плоскостям движения всех материальных точек шара:

RFJ

тр0

=

β

, (6.90)

где

0

J

– момент инерции шара относительно данной оси,

td

d

ω

β

=

– угловое ускорение шара. В (6.90) учтено, что моменты сил тяже-

сти и нормальной реакции доски равны нулю, поскольку линии их

действия проходят через ось вращения.

Дополним систему уравнений движения шара и доски

(6.87) – (6.90) уравнением кинематической связи, которое следует

из условия отсутствия проскальзывания между шаром и доской:

Raa

β

−

=

12

. (6.91)

Рис. 6.13

m

2

g

N

F

тр

Y

X

F

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

212

Учтем также, что момент инерции однородного шара относи-

тельно оси, проходящей через его центр масс (6.45) равен:

2

0

5

2

mRJ = . (6.92)

III. Решая систему уравнений (6.87), (6.89) – (6.92), получаем

искомые ускорения доски и центра шара:

21

1

27

7

mm

F

a

+

= ,

(6.93)

21

2

27

2

mm

F

a

+

=

. (6.94)

Определим условия, при которых движение шара будет про-

исходить без проскальзывания. Для движения шара по доске без

проскальзывания необходимо, чтобы сила трения в соответствии с

законом Амонтона–Кулона (см. п. 2.1.2 в Главе 2) удовлетворяла

неравенству:

NF

μ

≤

тр

. (6.95)

Здесь

μ

– коэффициент трения.

Модули сил трения и нормальной реакции опоры находим из

уравнения движения шара, записанного в проекциях на оси X и Y

выбранной системы координат (6.87) и (6.88) и подставляем в не-

равенство (6.95). В результате с учетом найденного ускорения цен-

тра шара (6.94) получим:

2

27

21

mm

gF

+

≤

μ

. (6.96)

Ответ:

21

1

27

7

mm

F

a

+

=

и

21

2

27

2

mm

F

a

+

=

при

2

27

21

mm

gF

+

≤

μ

.

Задача 6.6

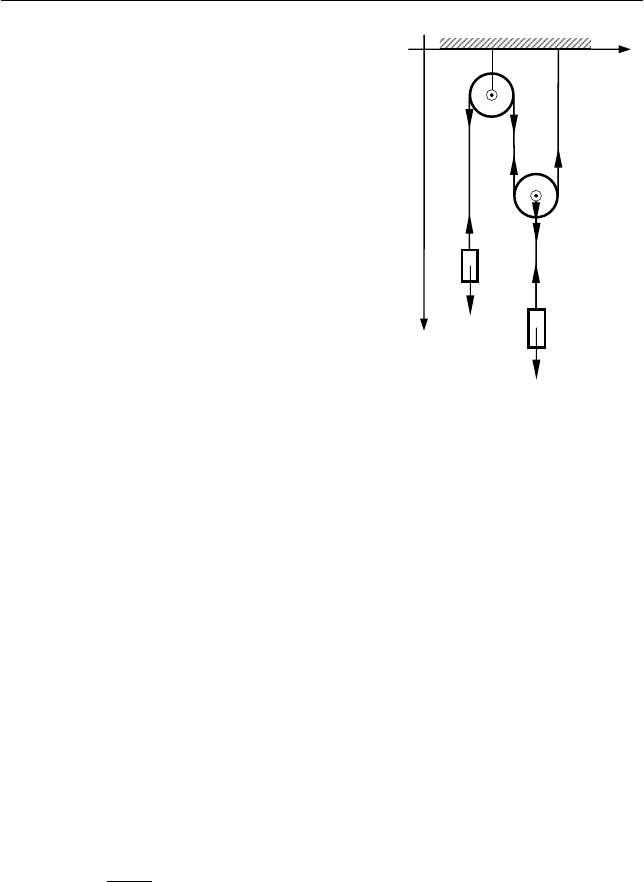
Система тел, состоящая из двух грузов, связанных между со-

бой с помощью невесомой нерастяжимой нити, и двух одинаковых

блоков, изображена на рис. 6.14. Ось левого блока закреплена, а

правый блок свободно лежит на нити. При движении тел системы

не происходит проскальзывания нити относительно поверхностей

блоков. Считая заданными массы грузов m

1

и m

2

, массы блоков M и

их радиусы R, определить ускорения грузов

a

1

и a

2

, а также разно-

Глава 6. Кинематика и динамика абсолютно твердого тела

213

сти сил натяжения нитей по обе сто-

роны каждого из блоков. Трением в

оси блока пренебречь.

Решение

I. Выберем лабораторную инер-

циальную систему отсчета, жестко

связанную с точкой подвеса оси лево-

го блока, оси X и Y декартовой сис-

темы координат которой изображены

на рис. 6.14. В рассматриваемой сис-

теме оба груза и незакрепленный блок

движутся поступательно вдоль оси X,

при этом блоки вращаются вокруг

собственных осей под действием сил

тяжести (m

1

g, m

2

g, Mg) и сил натяже-

ния нитей (T

1

, T

2

, T

3

и T

4

). Поскольку

массы блоков по условию задачи от-

личны от нуля, то силы натяжения нити слева и справа от блоков

различны.

II. Запишем уравнения движения грузов и центра масс неза-

крепленного блока в проекции на ось X выбранной системы коор-

динат:

1111

Tgmam −= , (6.97)

2222

Tgmam −= , (6.98)

4322

TTTMgMa

−

−+= . (6.99)

Уравнения моментов для вращающихся блоков относительно

осей, проходящих через их центры масс (см. рис. 6.14), имеют вид:

RTRTJ

3110

−=

β

, (6.100)

RTRTJ

3420

−=

β

, (6.101)

где

β

1

и

β

2

− угловые ускорения блоков, моменты инерции J

0

кото-

рых относительно указанных осей равны (6.44):

2

0

MR

J = . (6.102)

Дополним полученную систему уравнений уравнениями ки-

нематических связей, следующими из условий нерастяжимости

нитей и отсутствия проскальзывания нитей по блокам:

Рис. 6.14

T

3

T

2

m

1

g

m

2

g

X

Y

T

4

T

2

T

1

Mg

T

3

T

1

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

214

02

21

=

+

aa , (6.103)

Ra

11

β

=

, (6.104)

21

β

−

=

. (6.105)

В результате получена полная система уравнений для девяти

неизвестных величин:

1

a ,

2

a ,

1

T ,

2

T ,

3

T ,

4

T ,

1

β

,

2

β

и

0

J .

III. Выразим все силы натяжения нитей через ускорение a

1

,

используя уравнения (6.97), (6.98) и (6.100) − (6.105):

1111

amgmT −

=

, (6.106)

1

2

22

2

a

m

gmT −= , (6.107)

1113

2

a

M

mgmT

⎟

⎠

⎞

⎜

⎝

⎛

+−=

, (6.108)

()

1114

aMmgmT +−

=

. (6.109)

Нетрудно видеть, что искомые разности сил натяжения нитей

по обе стороны каждого из блоков равны:

14331

2

a

M

TTTT =−=−

. (6.110)

Подставляя (6.106) – (6.109) в уравнение (6.99) находим ис-

комое ускорение первого груза в проекции на ось X:

g

Mmm

a

44

224

21

1

++

−−

=

. (6.111)

Используя уравнение кинематической связи (6.103), получим

искомое ускорение второго груза также в проекции на ось X:

g

Mmm

mMm

a

44

2

21

12

2

++

−+

= . (6.112)

Искомые разности сил натяжения нитей (6.110) с учетом

(6.111) равны:

Mg

Mmm

TTTT

44

2

21

4331

++

−−

=−=− . (6.113)

Задача 6.7

В системе тел, показанной на рис. 6.15, известны масса груза

m

1

, масса ступенчатого блока m

2

, момент инерции блока J

0

относи-

тельно его оси и радиусы ступеней блока R

1

и R

2

(R

2

> R

1

). Масса

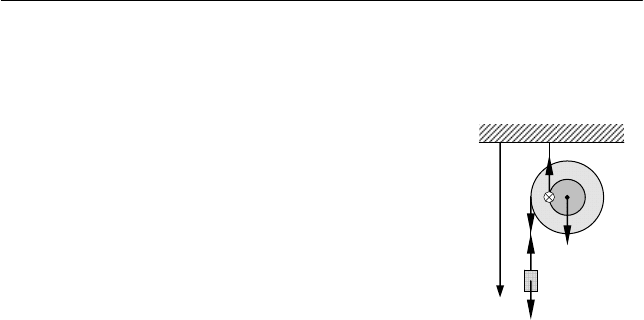
Глава 6. Кинематика и динамика абсолютно твердого тела

215

нитей пренебрежимо мала. Найти ускорения груза a

1

и центра масс

блока

a

2

в лабораторной системе отсчета.

Решение

I. Выберем лабораторную инерциаль-

ную систему отсчета, жестко связанную с по-

толком (см. рис. 6.15), ось Y декартовой сис-

темы координат которой направим вертикаль-

но вниз. В зависимости от соотношения между

массами тел системы блок может как в поло-

жительном, так и в отрицательном направле-

нии оси Y, совершая при этом чисто враща-

тельное

движение относительно мгновенной

оси вращения. Поскольку нить, прикрепленная

к потолку, нерастяжима, то мгновенная ось

вращения блока проходит через точку A соприкосновения блока и

этой нити. При этом мгновенная ось вращения перпендикулярна

плоскости чертежа, а ее выбранное положительное направление

указано на рис. 6.15.

II. Уравнение движения груза в проекции на ось Y (см.

рис. 6.15) имеет

вид:

Tgmam −=

111

, (6.114)

где T – сила натяжения нити, на которой подвешен груз.

Уравнение вращательного движения (уравнение моментов)

блока запишем относительно мгновенной оси вращения в лабора-

торной инерциальной системе отсчета:

)(

122

RRTgRmJ

−

=

β

. (6.115)

Здесь J – момент инерции блока относительно мгновенной оси,

β

–

угловое ускорение блока. В (6.114) учтено, что момент силы натя-

жения T

0

верхней нити, прикрепленной к потолку (рис. 6.15), отно-

сительно мгновенной оси вращения равен нулю.

Момент инерции блока относительно мгновенной оси выра-

зим через заданный в условии задачи момент инерции J

0

относи-

тельно его оси в соответствии с теоремой Гюйгенса-Штейнера

(6.42):

2

120

RmJJ += . (6.116)

Рис. 6.15

T

m

2

g

m

1

g

Y

T

0

A

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

216

Дополним уравнения (6.114) – (6.116) уравнениями кинема-

тической связи, которые следуют из условия нерастяжимости ни-

тей:

)(

121

RRa −−

=

β

, (6.117)

12

Ra

β

=

. (6.118)

III. Решая систему уравнений (6.114) – (6.118), получаем вы-

ражения для искомых ускорений груза a

1

и центра масс блока a

2

:

()()

()

12

0

2

12

2

121

12121

1

RR

JRmRRm

gRmRRm

a −

++−

−−

= , (6.119)

()()

()

1

0

2

12

2

121

12121

2

R

JRmRRm

gRmRRm

a

++−

−−

−= . (6.120)

Как видим, ускорения груза и центра блока направлены про-

тивоположно при любом соотношении масс груза и блока (см.

(6.119) и (6.120)), при этом каждое из тел изначально покоящейся

системы может как опускаться, так и подниматься в зависимости от

соотношения масс тел

системы и радиусов ступеней блока.

Если

12

1

2

1

RR

R

m

−

> , то груз будет опускаться с ускорением

1

a

(6.119), а центр блока будет подниматься с ускорением

12

1

12

RR

R

aa

−

−=

, модуль которого может быть как больше (при

12

2RR <

), так и меньше (

12

2RR >

) модуля ускорения груза

1

a

.

При обратном соотношении масс груз будет подниматься, а

центр блока опускаться с тем же соотношением ускорений.

Заметим, что в частном случае равенства радиусов ступеней

блока

12

RR

=

вне зависимости от соотношения масс груза и блока

ускорение груза

1

a равно нулю, а ускорение центра блока направ-

лено вниз и равно

g

JRm

Rm

a

0

2

12

2

12

2

+

=

. Для цилиндрического одно-

родного блока

2

120

2

1

RmJ = и ускорение его центра будет равно

ga

3

2

= .

Глава 6. Кинематика и динамика абсолютно твердого тела

217

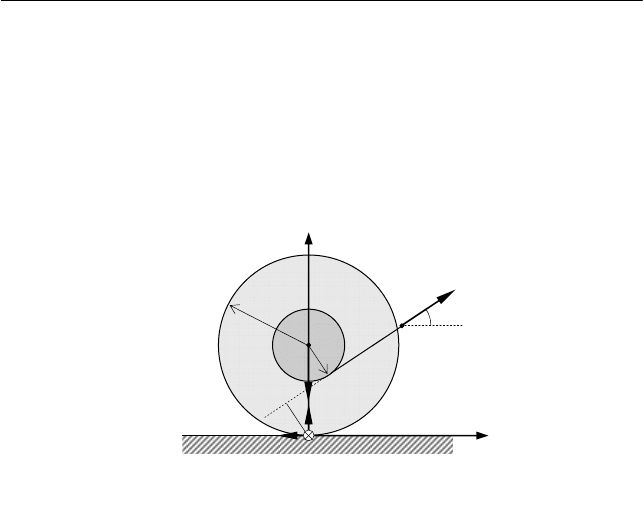
Задача 6.8

На лежащую на горизонтальной поверхности катушку массой

m = 100 г и моментом инерции J

0

= 400 г⋅см

2

относительно ее оси

намотана невесомая нерастяжимая нить. Внешний радиус катушки

равен

R = 4 см, а внутренний – r = 1 см. К концу нити под углом

α

= 60° к горизонтальной поверхности приложена сила F = 0.2 Н

(см. рис. 6.16).

Найти ускорение центра масс катушки

a для случая, когда

катушка движется в горизонтальном направлении без проскальзы-

вания и величину коэффициента трения, при котором такое движе-

ние возможно.

Решение

I. Выберем лабораторную инерциальную систему отсчета,

оси X, Y и Z декартовой системы координат которой направлены

так, как показано на рис. 6.16. Поскольку движение катушки явля-

ется плоским, то существует мгновенная ось вращения, направлен-

ная перпендикулярно параллельным плоскостям, в которых двига-

ются материальные точки катушки. В отсутствие проскальзывания

мгновенная ось вращения проходит через точки соприкосновения

катушки с горизонтальной поверхностью. Зададим в качестве по-

ложительного направления оси вращения положительное направ-

ление оси Z выбранной системы координат, начало отсчета кото-

рой совпадает с одной из точек соприкосновения (рис. 6.16).

II. Запишем систему уравнений движения катушки вместе с

намотанной на нее невесомой нитью относительно лабораторной

Рис. 6.16

F

α

N

mg

F

тр

Z

Y

d

X

r

R

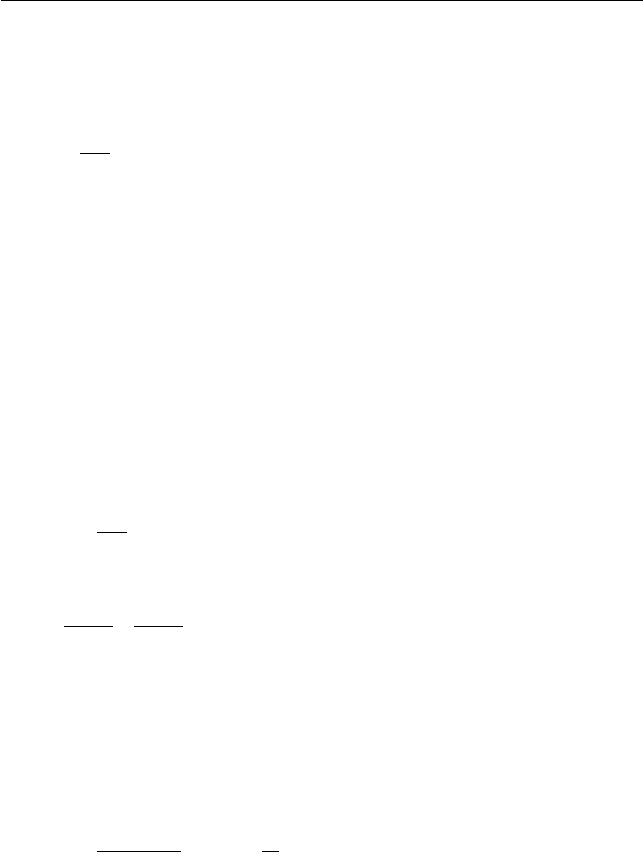
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

218

инерциальной системы отсчета, в которую войдут уравнение вра-

щательного движения вокруг мгновенной оси вращения и уравне-

ние движения центра масс катушки в проекциях на оси X и Y вы-

бранной системы координат:

Fd

dt

d

J =

ω

, (6.121)

α

sin0 FmgN +−

=

. (6.122)

тр

cos FFma −

=

α

, (6.123)

Здесь

J – момент инерции катушки относительно мгновенной оси

вращения,

ω

– угловая скорость вращения катушки, d – кратчайшее

расстояние от мгновенной оси вращения до линии действия силы

F

(плечо силы

F), F

тр

– сила трения покоя, действующая на катушку

со стороны горизонтальной поверхности,

N – сила нормальной ре-

акции опоры.

Уравнения (6.121) – (6.123) дополним уравнением кинемати-

ческой связи (в силу отсутствия проскальзывания при движении

катушки), теоремой Гюйгенса-Штейнера (6.42) для момента инер-

ции

J и очевидным геометрическим соотношением (см. рис. 6.16):

R

dt

d

a

ω

= , (6.124)

2

0

mRJJ += . (6.125)

R

rd

=+

αα

coscos

. (6.126)

Для определения коэффициента трения, при котором воз-

можно движение без проскальзывания, в соответствии с законом

Амонтона–Кулона (см. п. 2.1.2 в Главе 2) запишем:

NF

μ

≤

тр

. (6.127)

III. Решая систему уравнений (6.121) – (6.126) относительно

искомого ускорения центра масс катушки

a, получаем:

⎟

⎠

⎞

⎜

⎝

⎛

−

+

=

R

r

mRJ

FR

a

α

cos

2

0

2

. (6.128)

Для отсутствия проскальзывания катушки относительно го-

ризонтальной поверхности коэффициент трения должен удовле-

творять неравенству:

Глава 6. Кинематика и динамика абсолютно твердого тела

219

2

0

cos

sin

mRJ

mrRJ

Fmg

F

+

⋅

−

≥

α

μ

. (6.129)

Проанализируем полученный результат. В соответствии с

(6.128) направление ускорения

a определяется знаком выражения

⎟

⎠

⎞

⎜

⎝

⎛

−

R

r

α

cos . В том случае, когда точка пересечения линии дейст-

вия силы F и оси Y лежит левее начала отсчета системы координат,

катушка будет двигаться слева направо, поскольку

0cos >−

R

r

α

. В

противном случае качение будет происходить справа налево.

Подставляя численные значения физических величин, задан-

ные в условии задачи, получим для ускорения центра масс катушки

и коэффициента трения:

a = 0.4 м/с

2

,

μ

≥ 0,075.

Задача 6.9

Оси сплошного и тонкостенного цилиндров соединены неве-

сомой штангой. Цилиндры скатываются без проскальзывания по

наклонной поверхности клина с углом при основании

α

(см.

рис. 6.17). Радиусы цилиндров одинаковы и равны R, при этом мас-

са сплошного цилиндра равна m

1

, а тонкостенного − m

2

. Найти угол

α

, при котором цилиндры будут скатываться без проскальзывания.

Рис. 6.17

α

N

1

N

2

T

m

1

g

m

2

g

F

тр1

F

тр2

X

Y

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

220

Решение

I. Выберем лабораторную инерциальную систему отсчета,

жестко связанную с клином, оси X и Y декартовой системы коор-

динат которой изображены на рис. 6.17. На цилиндры в процессе

их плоского движения действуют силы тяжести

g

1

m и g

2

m , силы

трения

1тр

F и

тр2

F , силы нормальной реакции опоры

1

N и

2

N , а

также силы реакции штанги

T

(см. рис. 6.17).

II. Запишем уравнения движения центров масс цилиндров в

проекции на оси X и Y выбранной системы координат:

1тр11

sin FTgmam

−

−=

α

, (6.130)

2тр22

sin FTgmam

−

+=

α

, (6.131)

α

cos0

11

gmN −

=

, (6.132)

α

cos0

22

gmN −

=

, (6.133)

При записи уравнений (6.130) и (6.131) учтено, что силы ре-

акции штанги

T, действующие на цилиндры, равны по модулю. Это

легко доказать, используя уравнение движения невесомой штанги в

проекции на ось X и третий закон Ньютона. Ускорения центров

масс

a цилиндров также равны, поскольку штангу считаем абсо-

лютно твердым телом.

Уравнения моментов для цилиндров относительно осей вра-

щения, проходящих через их центры масс, имеют вид (см. (6.47)):

RFJ

1тр1

=

β

, (6.134)

RFJ

2тр2

=

β

. (6.135)

Здесь

1

J и

2

J − моменты инерции сплошного и тонкостенного ци-

линдров относительно осей, проходящих через их центры масс со-

ответственно;

β

– угловое ускорение, одинаковое для сплошного и

тонкостенного цилиндров в силу уравнения кинематической связи,

которое следует из условия качения цилиндра без проскальзыва-

ния:

aR

=

β

. (6.136)

Воспользуемся известными выражениями для моментов

инерции однородных сплошного (6.44) и тонкостенного цилиндров

относительно осей, проходящих через их центры масс:

2

1

Rm

J = , (6.137)

Русаков В.С. и др. Механика. Методика решения задач

Подождите немного. Документ загружается.