Русаков В.С. и др. Механика. Методика решения задач

Глава 5. Кинематика в теории относительности

181

Ответ:

ϑϑ

tg

2

3

tg =

′

,

2

cos3

2

ϑ

+

=

′

LL .

Задача 4

Космонавт спустя время

0

τ

(по собственным часам) после

старта получает радиограмму с сообщением о рождении внука.

Тотчас же, для того, чтобы внук получил поздравление вовремя, он

посылает ответную радиограмму, в которой поздравляет внука с

совершеннолетием (возраст равен Т). Какова скорость космическо-

го корабля?

Ответ:

22

0

4 TTcV +=

τ

.

Задача 5

Система отсчета S' движется относительно лабораторной

системы отсчета S

со скоростью V = c/2 в сторону, противополож-

ную оси X. В системе отсчета S частица движется со скоростью

U = c/2 под углом

ϑ

к оси X. Найти модуль скорости частицы U

′

в

системе отсчета S'. Определить, какой угол

ϑ

′

составляет скорость

частицы с осью

X' системы отсчета S'.

Ответ:

ϑϑ

ϑ

2

sincos88

cos4

−+

+

=

′

c

U,

()

ϑ

cos12

sin3

tg

+

=

′

.

Задача 6

Два космических корабля летят вдоль одной прямой в одном

направлении со скоростями

1

V >

2

V . Со второго корабля вдогонку

первому посылается два электромагнитных импульса с интервалом

времени

τ

1

относительно лабораторной системы отсчета. С каким

интервалом времени

τ

2

относительно той же системы отсчета они

вернутся назад после отражения от первого корабля?

Ответ:

⎟

⎠

⎞

⎜

⎝

⎛

+

−

⎟

⎠

⎞

⎜

⎝

⎛

−

+

=

2

1

12

Vc

ττ

.

Задача 7

Два события совершаются на расстоянии l = 6⋅10

5

км друг от

друга с промежутком времени

τ

= 1 с относительно некоторой

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

182

инерциальной системы отсчета. С какой скоростью V должен ле-

теть космический корабль, чтобы в системе отсчета, связанной с

кораблем, эти события стали одновременными?

Ответ:

м/с105,1

8

2

⋅==

l

c

V

τ

.

Задача 8

В системе отсчета S′, движущейся со скоростью 2/c вдоль

оси X лабораторной системы отсчета S, движется тело небольших

размеров со скоростью

2/c под углом

α

′ к оси X'. Найти угол

α

,

который составляет скорость тела с осью X в системе S.

Ответ:

2cos2

sin3

tg

+

′

=

α

Задача 9

Две частицы с одинаковыми скоростями V движутся вдоль

одной прямой и попадают в мишень с интервалом времени

τ

в

системе отсчета, связанной с мишенью. Найти расстояние l между

летящими частицами в системе отсчета, связанной с частицами.

Ответ:

()

2

/1 cV

V

l

−

=

τ

.

Задача 10

Космический корабль удаляется от Земли, двигаясь сначала

со скоростью

1

υ

, потом со скоростью

2

υ

. С точки зрения космо-

навта, находящегося на космическом корабле, время движения со

скоростями

1

υ

и

2

υ

одинаково. Какое расстояние L пролетит ко-

рабль, если время движения корабля по Земным часам равно Т?

(Пренебречь временем, затраченным на изменение скорости кораб-

ля.)

Ответ:

TL

21

2211

γγ

γυγυ

+

= ,

где

()

2

1

/1

1

c

υ

γ

−

= и

()

2

/1

1

c

υ

γ

−

= .

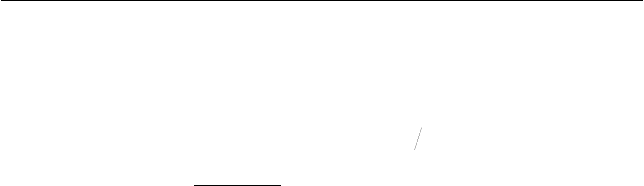
Глава 5. Кинематика в теории относительности

183

Задача 11

На легкую неподвижную частицу налетает тяжелая плита.

Определить скорость V, приобретенную частицей после упругого

столкновения с плитой, движущейся в направлении, перпендику-

лярном своей плоскости со скоростью

3c

=

υ

.

Ответ:

()

c

V 6,0

/1

2

=

+

=

υ

.

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

184

ГЛАВА 6

КИНЕМАТИКА И ДИНАМИКА АБСОЛЮТНО

ТВЕРДОГО ТЕЛА

6.1. Теоретический материал

6.1.1. Кинематика абсолютно твердого тела

Абсолютно твердое тело – тело (система материальных то-

чек), расстояния между двумя любыми материальными точками

которого можно считать постоянными в условиях данной задачи.

Рассмотрим движение абсолютно твердого тела относитель-

но лабораторной системы отсчета S. Для этого жестко свяжем

сис-

тему отсчета S' с этим телом. Таким образом, интересующее нас

абсолютно твердое тело выступает в качестве тела отсчета системы

S'.

Запишем формулы, связывающие кинематические характе-

ристики некоторой материальной точки относительно двух произ-

вольно движущихся относительно друг друга систем отсчета S и S'

(см. Главу 4):

'

r

R

r

+

=

, (6.1)

[]

'υωr'Vυ ++

=

, (6.2)

[] [][]

[

]

'aωυ'2ωr'ωr'ωAa

+

++

=

&

. (6.3)

Здесь

)(tr

,

)(' tr

− радиус-векторы, )(tυ , )(tυ

′

− скорости и )(ta ,

)(ta

′

− ускорения некоторой материальной точки относительно

систем отсчета S и S' соответственно;

)(tR , )(tV и )(tA – радиус-

вектор, скорость и ускорение начала системы отсчета S', которое

может и не совпадать с материальной точкой рассматриваемого

абсолютно твердого тела; )(

tω и )(tω

&

– угловая скорость и угловое

ускорение системы S' (абсолютно твердого тела) вокруг оси враще-

ния, проходящей через начало системы отсчета S' (рис. 6.1).

Если некоторая материальная точка M (см. рис. 6.1) принад-

лежит абсолютно твердому телу (телу отсчета системы S'), то, по-

скольку )(tυ

′

и )(ta

′

, для этой точки:

'

r

R

r

+

=

, (6.4)

[]

ωr'Vυ +

=

, (6.5)

[] [][]

ωr'ωr'ωAa ++

=

&

. (6.6)

Глава 6. Кинематика и динамика абсолютно твердого тела

185

Из уравнения для скорости произвольной материальной точ-

ки абсолютно твердого тела (6.5) следует принцип суперпозиции

движений (материальных точек) абсолютно твердого тела.

Принцип суперпозиции движений абсолютно твердого

тела

– любое перемещение абсолютно твердого тела (материаль-

ных точек этого тела) в пространстве можно представить как су-

перпозицию последовательно осуществляемых

поступательного

движения этого тела (параллельного переноса со скоростью

V ) и

поворота вокруг оси вращения (вращательного движения с угловой

скоростью

ω ).

Поступательное движение абсолютно твердого тела – дви-

жение, при котором прямая, соединяющая любые две материаль-

ные точки тела, перемещается параллельно самой себе. Для описа-

ния поступательного движения абсолютно твердого тела достаточ-

но описать движение любой материальной точки этого тела.

Произвольное движение абсолютно твердого тела (и жестко

связанной с ней системы отсчета S') однозначно задается

законом

движения любой материальной точки тела (начало системы отсчета

S' совпадает с этой точкой тела) )(

tR и законом изменения угловой

скорости вращения тела (системы отсчета S') относительно этой

точки )(

tω .

Число степеней свободы

механической системы – число не-

зависимых физических величин, так называемых

обобщенных ко-

ординат

, однозначно определяющих положение тел системы в

пространстве.

Рис. 6.1. Радиус-векторы произвольной материальной точки M

абсолютно твердого тела в лабораторной системе отсче-

та S и системе отсчета S', связанной с телом

S

r

O

'r

S'

ω

R

O'

M

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

186

У абсолютно твердого тела шесть степеней свободы. Напри-

мер, три координаты произвольной материальной точки тела, два

угла, задающих направление прямой, соединяющей две точки и

угол поворота тела вокруг этой прямой.

Плоское движение абсолютно твердого тела

Плоское движение

– движение тела, при котором траекто-

рии всех материальных точек тела лежат в параллельных плоско-

стях. В случае плоского движения абсолютно твердое тело имеет

три степени свободы.

Вращательное движение абсолютно твердого тела вокруг

неподвижной оси – плоское движение, при котором материальные

точки тела двигаются по окружностям с центрами, лежащими на

этой оси, называемой

осью вращения. В этом случае абсолютно

твердое тело обладает одной степенью свободы.

При плоском движении скорость )(

tυ и ускорение )(ta мате-

риальной точки абсолютно твердого тела лежат все время в плос-

кости движения P этой точки (см. рис. 6.2).

Действительно, пусть cons

t

−

n – единичный вектор нормали

к плоскости движения, тогда

()

0

d

=

⎟

⎠

⎞

⎜

⎝

⎛

=

t

r

nnυ

,

(

)

()()()

0==+=

∂

naυnυn

nυ

&&

t

. (6.7)

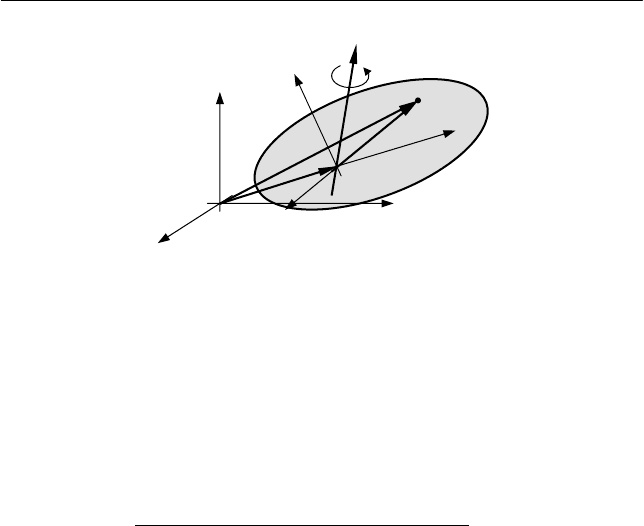
Рис. 6.2. Кинематические характеристики материальной точки М

абсолютно твердого тела при его плоском движении

S

r

O

'r

S'

ω

υ

n

P

a

O'

M

Глава 6. Кинематика и динамика абсолютно твердого тела

187

Угловая скорость ω и угловое ускорение ω

&

абсолютно

твердого тела в случае плоского движения всегда перпендикулярны

плоскости движения.

Действительно, умножим обе части уравнения взаимосвязи

скоростей (6.5) скалярно на нормаль к плоскости движения. Так как

результат будет справедлив при любых )(tV и )(' tr , то:

()( )

{

[]

()

0'

0

=

+=

=

321

ωrnnVnυ

,

Vn

⊥

, ωn || и Vω

⊥

. (6.8)

Умножим обе части уравнения взаимосвязи ускорений (6.6)

скалярно на нормаль к плоскости движения. Так как результат бу-

дет справедлив при любых )(

tA и )(' tr , то:

()( )

{

[]

()

[

]

[

]

(

)

0''

||,00

0

=

+

+=

==

=

434214321

&

ωn

ωrωnrωnnAna ,

An

⊥

и ωn

&

|| . (6.9)

Покажем, что в случае плоского движения абсолютно твер-

дого тела в любой момент времени найдется такой вектор

0

r

′

, что

[][]

0

' rωωrVυ

′

=+

=

. (6.10)

Действительно, преобразуя (6.10), получим:

[]

0',

0

=

′

−

+

rrωV ,

0

' rrd

′

−

≡

,

[

]

[

]

0,

=

+

ωdVn .

При этом будем искать такой вектор d , что nd

⊥

, тогда:

[] [][][]

(

)

(

)

[

]

(

)

0

=

−

=

−

+

=+

=

nωdnVnωdndωnVωdnnV

321

,

[]

()

[]

ω

nV

nω

nV

d ==

. (6.11)

И, наконец, найдем радиус-вектор нового начала системы от-

счета

0

R , для которой будет выполняться соотношение (6.10):

00

' rRrRr

′

+=+

=

,

[

]

ω

nV

RdRrrRR +=+=

′

−+=

00

'

. (6.12)

Итак, плоское движение абсолютно твердого тела в течение

бесконечно малого интервала времени можно представить, как

"чистый" поворот относительно некоторой оси – мгновенной оси

вращения

.

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

188

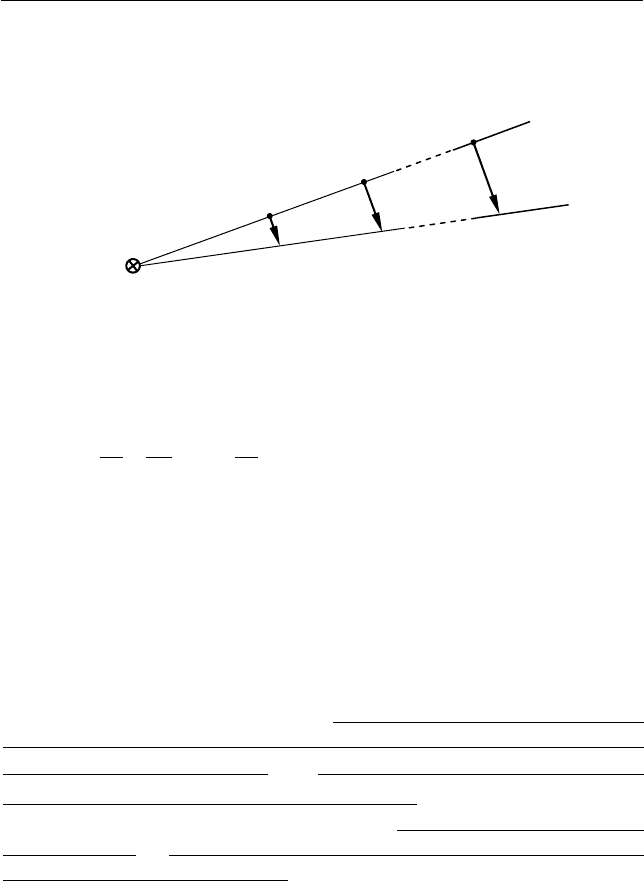
На рис. 6.3 изображена векторная диаграмма скоростей мате-

риальных точек тела, лежащих в плоскости движения на одной

прямой, проходящей через мгновенную ось вращения.

Как видно на рис. 6.4, в этом случае выполняется соотноше-

ние:

i

RRR

υυυ

ω

==== K

2

1

, (6.13)

где

i

υ

– скорость материальной точки абсолютно твердого тела, а

R

i

– расстояние от этой материальной точки до мгновенной оси

вращения.

Мгновенная ось вращения – ось вращения, относительно

которой в течение бесконечно малого интервала времени можно

представить абсолютно твердого тела, как "чистый" поворот, т.е.

представить скорость движения произвольной материальной точки

тела в виде (6.10).

В общем случае положение мгновенной оси вращения изме-

няется относительно абсолютно твердого тела в выбранной систе-

мы отсчета – радиус-вектор

0

R , задающий положение мгновенной

оси, является функцией времени (см. (6.12)).

Мгновенная ось вращения всегда перпендикулярна плоско-

сти движения и проходит через неподвижную в данный момент

времени материальную точку абсолютно твердого тела или точку

пространства, которая жестко связана с этим абсолютно твердым

телом.

Рис. 6.3. Векторная диаграмма скоростей материальных точек

абсолютно твердого тела при его плоском движении

1

υ

R

1

ω

R

2

R

i

2

υ

i

υ

Глава 6. Кинематика и динамика абсолютно твердого тела

189

Движение абсолютно твердого тела, закрепленного в точке

Если абсолютно твердое тело (тело отсчета системы S') за-

креплено в точке, покоящейся относительно системы S, то, совмес-

тив начала отсчета обеих систем (

0

=

R

,

0

=

V

,

0

=

A

), получим:

'

r

R

r

+

=

, (6.14)

[

]

ωr'υ

=

, (6.15)

[] [][]

ωr'ωr'ωa +

=

&

. (6.16)

Из уравнения (6.15) для скорости произвольной материаль-

ной точки абсолютно твердого тела, закрепленного в точке, следует

теорема Эйлера.

Теорема Эйлера – абсолютно твердое тело, закрепленное в

точке, может быть переведено из одного положения в любое другое

одним поворотом вокруг неподвижной оси, проходящей через точ-

ку закрепления. Причем это утверждение справедливо как для бес-

конечно малого, так и для конечного поворота. Однако результат

двух конечных поворотов зависит от их последовательности, в от-

личие от двух бесконечно малых поворотов.

Если система отсчета S

1

с общим началом с системой S вра-

щается относительно нее с угловой скоростью

Ω и абсолютно

твердое тело, закрепленное в начале отсчета этих систем, вращает-

ся с угловой скоростью

1

ω относительно системы S

1

, то в соответ-

ствии с (6.5):

{

[]

[

]

[

]

[

]

[

]

'',''''

11

0

ωrrωΩrωΩrυΩrVυ

=

+

=

+

=++

=

, (6.17)

.ωΩω

1

+

=

(6.18)

Здесь

υ

− скорость материальной точки абсолютно твердого тела

относительно системы S,

ω

− угловая скорость вращения абсо-

лютно твердого тела относительно той же системы.

Как видим, угловая скорость

ω

вращения данного тела, за-

крепленного в точке относительно первой системы отсчета, будет

равна сумме угловых скоростей второй системы отсчета

1

ω и тела

относительно этой системы

2

ω .

Как и в случае плоского движения, движение абсолютно

твердого тела, закрепленного в точке, можно представить как "чис-

тый" поворот вокруг мгновенной оси вращения.

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

190

6.1.2. Динамика абсолютно твердого тела

Момент импульса

L материальной точки относительно

некоторой точки пространства

– векторное произведение радиус-

вектора

r материальной точки относительно данной точки про-

странства на ее импульс

p в заданной системе отсчета:

[]

rpL

=

. (6.19)

Момент импульса L механической системы относитель-

но точки

– сумма моментов импульсов

i

L материальных точек,

входящих в систему:

∑

=

i

LL . (6.20)

Найдем связь между моментом импульса механической сис-

темы

L относительно произвольной неподвижной точки О и мо-

ментом импульса этой системы

0

L относительно ее центра масс O'

в лабораторной системе отсчета (см. рис. 6.4).

Радиус-вектор

i-ой материальной точки

i

r

относительно точ-

ки О равен:

ii

rrr

′

+

=

цм

, (6.21)

где

цм

r

– радиус-вектор центра масс относительно точки О,

i

r

′

–

радиус-вектор материальной точки системы относительно ее цен-

тра масс.

Момент импульса системы материальных точек относитель-

но точки О в соответствии с (6.19) и (6.20) равен:

Рис. 6.4. Связь между радиус-векторами матери-

альной точки в лабораторной системе

отсчета S и системе центра масс S'

m

i

r

'

i

r

O

цм

r

O'

S

S'

Русаков В.С. и др. Механика. Методика решения задач

Подождите немного. Документ загружается.