Русаков В.С. и др. Механика. Методика решения задач

Глава 5. Кинематика в теории относительности

151

Принципиально важно, что эти два события происходят од-

новременно

в системе S: t

1

= t

2

, Δt = t

2

–t

1

= 0. Для системы S' эти

события будут происходить не одновременно. В соответствии с

(5.4) для пространственных интервалов

12

Δ xxx

−

=

и

12

Δ xxx

′

−

′

=

′

можно записать:

()

x

cV

x

x Δ

/1

Δ

2

γ

=

−

=

′

или

γ

x

′

=

Δ

Δ . (5.7)

Другими словами,

для системы отсчета, в которой события

происходят одновременно, наблюдается сокращение простран-

ственного интервала между этими событиями (по сравнению с

любой другой системой отсчета) вдоль направления относи-

тельного движения систем

.

Если событиями являются измерения координат линейки (см.

рис. 5.4), то:

()

l

cV

l

γ

=

−

=

2

0

/1

или

γ

0

l

l = . (5.8)

Здесь

xl

′

≡ Δ

0

– собственная длина линейки (длина линейки в не-

подвижной относительно линейки системе отсчета S', при этом из-

мерение координат концов линейки может происходить в разные

моменты времени);

xl Δ≡ – длина линейки в системе отсчета S,

относительно которой линейка движется со скоростью

V (измере-

ние координат концов линейки должно происходить в один и тот

же момент времени).

5.1.4. Пространственно-временной интервал

Пространственно-временной интервал между двумя со-

бытиями:

()()()()

=−−−+−+−≡

2

12

2

12

2

12

2

1212

ttczzyyxxS

2

12

22

12

22222

ΔΔΔΔ tcrtczyx −=−++= . (5.9)

Здесь 0ΔΔΔ

222

12

≥++= zyxr – пространственный интервал

(расстояние между точками пространства, в которых произошли

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

152

рассматриваемые события) и 0Δ

12

≥= tt – временной интервал

между событиями

.

Воспользовавшись преобразованиями Лоренца (5.2), легко

показать, что

пространственно-временной интервал между дву-

мя событиями одинаков во всех инерциальных системах отсче-

та

, то есть является инвариантом по отношению к преобразовани-

ям Лоренца при переходе от одной инерциальной системы отсчета

к другой:

1212

SS

′

=

. (5.11)

Заметим, что при этом переходе пространственный

r

12

и временной

t

12

интервалы либо оба уменьшаются, либо оба увеличиваются.

Пространственноподобный интервал − вещественный про-

странственно-временной интервал между двумя событиями, для

которого 0

2

12

>S . В этом случае: r

12

> ct

12

.

Свойства пространственноподобного интервала

между двумя событиями

1. Существует такая инерциальная система отсчета, в кото-

рой события происходят одновременно, но в разных точках про-

странства. В этой системе отсчета пространственный интервал

12

r

′

между событиями принимает минимальное значение:

1212

2

12

22

1212

rStcrS

′

=

′

=−= , (5.12)

2

12

22

1212

tcrr −=

′

. (5.13)

2. Не существует

системы отсчета, в которой события проис-

ходят в одной точке пространства.

3. События, связанные пространственноподобным интерва-

лом, в результате перехода в другую систему отсчета могут проис-

ходить во времени в обратной последовательности.

4. Эти события не могут быть связаны причинно-

следственной связью, поскольку для этого потребовалась бы ско-

рость передачи сигнала, превышающая скорость света:

0

2

12

>S ,

1212

ctr >

, c

t

r

>=

12

υ

. (5.14)

5. Эти события не могут происходить с одним и тем же телом

(достаточно малым, чтобы считать, что события происходят в од-

Глава 5. Кинематика в теории относительности

153

ной и той же точке пространства относительно системы отсчета,

связанной с этим телом), поскольку тело не может двигаться со

скоростью, превышающей скорость света.

Времениподобный интервал − мнимый пространственно-

временной интервал между двумя событиями, для которого 0

2

12

<S .

В этом случае:

r

12

< ct

12

.

Свойства времениподобного интервала

между двумя событиями

1. Существует такая инерциальная система отсчета, в кото-

рой оба события происходят в одной и той же точке пространства,

но в разное время. В этой системе отсчета временной интервал

12

t

′

между событиями принимает минимальное значение:

()

,

2

12

22

12

22

12

2

12

1212

2

12

22

1212

tctcrS

ticStcrS

′

−=−=

′

=

′

=−=

(5.15)

2

12

22

1212

tcr

c

i

t −−=

′

. (5.16)

2. Не существует

системы отсчета, в которой события проис-

ходят в одно и то же время:

0

12

=

′

t

.

3. События, связанные времениподобным интервалом, в ре-

зультате перехода в другую систему отсчета не могут происходить

во времени в обратной последовательности.

4. Эти два события могут быть связаны причинно-

следственной связью, поскольку для этого требуется скорость пе-

редачи сигнала меньше скорости света:

0

2

12

<S ,

1212

ctr < ,

c

t

r

<=

12

υ

. (5.17)

5. Эти события могут происходить с одним и тем же телом

,

поскольку тело может двигаться со скоростью, меньшей скорости

света, то

ct

12

> r

12

и 0

2

12

<S .

Светоподобный интервал − нулевой пространственно-

временной интервал между двумя событиями

0

2

12

=S .

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

154

Свойства светоподобного интервала

между двумя событиями

1. Если события происходят в одной точке пространства, то

они происходят одновременно (и наоборот) в любой инерциальной

системе отсчета:

0

2

12

22

1212

=−= tcrS , 00

1212

=

⇔

=

tr . (5.18)

2. Не существует инерциальной системы отсчета, в которой

два события, разделенные пространственным интервалом происхо-

дят одновременно или разделенные временным интервалом, про-

исходят в одной точке пространства.

3. События, связанные светоподобным интервалом, в резуль-

тате перехода в другую систему отсчета не могут происходить во

времени в обратной последовательности.

Докажем это. Для рассматриваемых событий

tcx ΔΔ

±

=

, сле-

довательно, в соответствии с преобразованиями Лоренца для ин-

тервалов (5.4), можно записать:

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅−=

⎟

⎠

⎞

⎜

⎝

⎛

−=

′

c

V

t

x

c

V

tx

c

V

tt

m

1Δ

Δ

1ΔΔΔΔ

22

γγγ

. (5.19)

Как видим, знак временного интервала

t

′

Δ совпадает со знаком

интервала

tΔ при любых возможных скоростях движения системы

S' относительно системы S.

4. Эти два события могут быть связаны причинно-

следственной связью, если используется сигнал, передающийся со

скоростью света:

0

2

12

=S ,

1212

ctr =

, c

t

r

==

12

υ

. (5.20)

5. Эти события не могут происходить с одним и тем же те-

лом, имеющим массу покоя, поскольку оно не может двигаться со

скоростью света.

Понятия времениподобный, пространственноподобный и

светоподобный интервалы – понятия абсолютные

, не зависящие от

выбора инерциальной системы отсчета.

5.1.5. Преобразование (сложение) скоростей

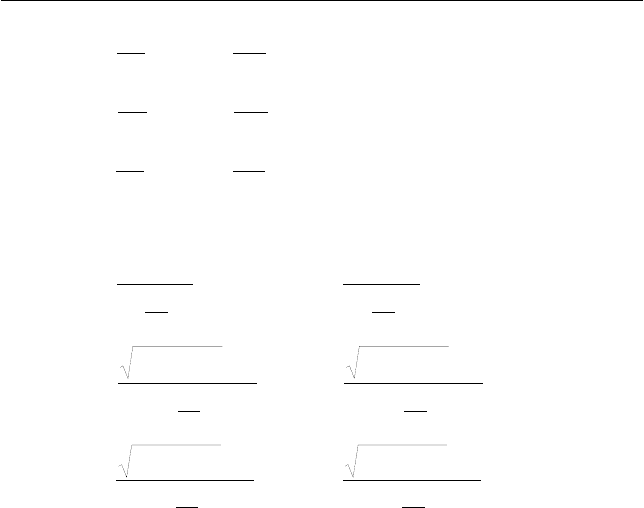
В соответствии с преобразованиями Лоренца (5.2) и опреде-

лением скорости (см. п. 1.1 в Главе 1)

Глава 5. Кинематика в теории относительности

155

⎪

⎩

⎪

⎨

⎧

=

;

d

,

d

,

d

t

z

t

y

t

x

z

y

x

υ

⎪

⎩

⎪

⎨

⎧

′

=

′

=

′

=

′

;

d

,

d

,

d

t

z

t

y

t

x

z

y

x

υ

(5.21)

получим:

()

⎪

⎩

⎪

⎨

⎧

−

⋅−

=

′

−

⋅−

=

′

−

=

′

;

1

/1

,

1

/1

,

1

2

x

z

x

y

x

c

V

cV

c

V

cV

c

V

υ

()

⎪

⎩

⎪

⎨

⎧

′

+

′

⋅−

=

′

+

′

⋅−

=

′

+

′

=

.

1

/1

,

1

/1

,

1

2

x

z

x

y

x

c

V

cV

c

V

cV

c

V

υ

(5.22)

Относительная скорость – скорость движения одного тела

относительно системы отсчета, связанной с другим телом. Эта ско-

рость не может быть больше скорости света.

Скорость сближения тел – скорость изменения расстояния

между телами в данной системе отсчета. Эта скорость может быть

больше скорости света.

5.2. Основные типы задач и методы их решения

5.2.1. Классификация задач кинематики

в теории относительности

Большинство задач кинематики в теории относительности

можно условно отнести к следующим типам задач или их комбина-

циям. Задачи на:

1) преобразования Лоренца или их следствия ("относитель-

ность одновременности", "замедление времени" и "сокращение

длины");

2) инвариантность пространственно-временных интервалов;

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

156

3) преобразования скоростей.

Как правило, один из типов задач имеет основное, другие –

подчиненное по отношению к условию задачи значение.

5.2.2. Общая схема решения задач кинематики

в теории относительности

I.

Определиться с событиями и системами отсчета.

1. Нарисовать чертеж, на котором изобразить рассматривае-

мые тела (если это необходимо).

2. Выбрать движущиеся друг относительно друга инерциаль-

ные системы отсчета и изобразить на чертеже их системы

координат (из соображений удобства).

3. Изобразить и обозначить скорости тел.

4. Выбрать интересующие нас события и записать их про-

странственно-временные координаты относительно вы-

бранных систем отсчета.

II. Записать полную систему уравнений для искомых величин.

1. Записать преобразования Лоренца или их следствия (для

задач типа (1)).

2. Записать пространственно-временные интервалы между

событиями (для задач типа (2)).

3. Записать формулы преобразования скоростей (для задач

типа (3)).

4. Использовать условия задачи (например, соотношения ме-

жду характеристиками системы и пространственно-

временными координатами событий).

III. Получить искомый результат в аналитическом и числен-

ном видах.

1. Решить систему полученных уравнений.

2. Провести анализ решения (рассмотреть характерные слу-

чаи).

3. Получить численный результат.

Глава 5. Кинематика в теории относительности

157

5.3. Примеры решения задач

Задача 5.1

(Преобразования Лоренца или их следствия)

Стержень пролетает с постоянной скоростью мимо метки,

неподвижной в системе отсчета S. Время пролета в этой системе

Δt = 20 нс. В системе же отсчета S', связанной со стержнем, метка

движется вдоль него в течение Δt' = 25 нс. Найти собственную дли-

ну стержня.

Решение

I. Пусть стержень, а значит и система S', движутся со скоро-

стью V вдоль оси X системы S. С такой же по величине скоростью,

но в обратном направлении, движется метка относительно стержня.

Для решения задачи воспользуемся рис. 5.4 (см.

п. 5.1. Теоретический материал). Определим события А и В, как

моменты пролета метки мимо обоих концов стержня.

Обозначим

пространственно-временные координаты этих событий, как (

1

x

′

,

1

t

′

)

и (

2

x

′

,

2

t

′

) в системе отсчета S' и как (

1

x

,

1

t

) и (

2

x

,

2

t

) в системе от-

счета S. Заметим, что в соответствии с выбором событий

21

xx = .

II. Искомая собственная длина стержня

0

l равна простран-

ственному интервалу между событиями А и В в системе отсчета,

связанной со стержнем −

120

xxl

′

−

′

=

. Поскольку метка движется

относительно стержня со скоростью V, то

tVl

′

=

Δ

0

, (5.23)

где

12

Δ ttt

′

−

′

=

′

− временной интервал между рассматриваемыми

событиями в системе отсчета S'.

Для нахождения V запишем преобразования Лоренца для

временных интервалов t

′

Δ и

12

Δ ttt

−

=

(см. (5.5)):

()

2

/1

Δ

cV

t

−

=

′

. (5.24)

Заметим, что в данном случае сокращается интервал времени

tΔ

, поскольку в системе отсчета S события А и В происходят в од-

ной точке пространства (наблюдается "замедление времени").

III. Используя (5.24), определим величину скорости V:

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

158

2

Δ

1

⎟

⎠

⎞

⎜

⎝

⎛

′

−=

t

cV . (5.25)

В соответствии с (5.23) и (5.25) искомая собственная длина

стержня (длина стержня в неподвижной относительно него системе

отсчета S') равна

2

0

'Δ

Δ

1ΔΔ

⎟

⎠

⎞

⎜

⎝

⎛

−

′

=

′

=

t

tctVl . (5.26)

Подставив в (5.26) значения Δt = 20 нс и Δt' = 25 нс, заданные

в условии задачи, а также значение скорости света м/с103

8

⋅≅c ,

получим:

=

0

l 4,5 м.

Задача 5.2

(Преобразования Лоренца или их следствия)

Собственное время жизни некоторой нестабильной частицы

=

0

Δt

10 нс. Какой путь пролетит эта частица, двигаясь с постоян-

ной скоростью, до распада в лабораторной системе отсчета, где ее

время жизни =tΔ 20 нс?

Решение

I. Выберем системы отсчета. Свяжем систему отсчета S' с

движущейся частицей. Следовательно, система S' движется отно-

сительно лабораторной системы S со скоростью движения частицы

V. Для решения задачи воспользуемся рис. 5.3 (см.

п. 5.1. Теоретический материал). Определим события А и В как со-

бытия, состоящие в рождении и распаде частицы соответственно.

Пусть пространственно-временные координаты этих

событий в

системе отсчета S равны (

1

x ,

1

t ) и (

2

x ,

2

t ), а в системе отсчета S' –

(

1

x

′

,

1

t

′

) и (

2

x

′

,

2

t

′

), причем

21

xx

′

=

′

. Собственное время жизни неста-

бильной частицы

0

Δt – время жизни в системе отсчета S', в которой

эти два события происходят в одной и той же точке пространства:

120

ΔΔ tttt

′

−

′

=

′

= (5.27)

II. Искомый путь l, который пролетит частица до своего рас-

пада в лабораторной системе отсчета S определяется ее скоростью

и временем жизни частицы в этой системе:

tVl Δ= . (5.28)

Глава 5. Кинематика в теории относительности

159

Для нахождения скорости частицы (а, следовательно, и ско-

рости движущейся системы отсчета S') воспользуемся следствием

преобразований Лоренца – "замедлением времени". Поскольку в

системе отсчета S' события А и В происходят в одной точке про-

странства, то, согласно (5.5), должно наблюдаться сокращение ин-

тервала времени в системе S' между рассматриваемыми событиями.

Таким образом, собственное время жизни и

время жизни в лабора-

торной системе отсчета связаны следующим соотношением:

()

2

0

/1Δ

Δ

Δ cVt

t

t −==

γ

. (5.29)

III. Используя (5.29), определим скорость системы отсчета S':

2

0

Δ

1

⎟

⎠

⎞

⎜

⎝

⎛

−=

t

cV . (5.30)

Подставляя полученное выражение (5.30) для скорости в

(5.28), определим искомый путь l, который пролетит частица до

своего распада в лабораторной системе отсчета S:

2

0

Δ

1Δ

⎟

⎠

⎞

⎜

⎝

⎛

−=

t

tcl . (5.31)

Подставив в (5.31) численные значения величин

0

Δt и

tΔ

,

заданные в условии задачи, получаем:

l = 5,2 м.

Задача 5.3

(Преобразования Лоренца или их следствия)

Система отсчета S' движется относительно системы S вдоль

оси X с постоянной скоростью V = 0,9c. В каждой системе в точках

с координатами –200 м, –100 м, 0 м, 100 м и 200 м находятся оди-

наковые синхронизованные часы. За начало отсчета времени в обе-

их системах отсчета взят такой момент, когда часы, неподвижные

относительно системы S и имеющие координату x = 0 м, окажутся

напротив часов, неподвижных относительно системы S' и имеющих

координату x' = 0 м. Определить время, которое в этот момент бу-

дут показывать часы, а также их координаты "с точки зрения" на-

блюдателей, находящихся как в системе S, так и в системе S'. Изо-

бразить расположение часов обеих

систем и примерное положение

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

160

стрелок этих часов в этот момент времени относительно различных

систем отсчета.

Решение

I. Пусть событие A

j

(j =1, 2, 3, 4, 5) заключается в том, что в

момент времени

0

A

=

j

t по часам системы S фиксируется показа-

ния j-ых часов, расположенных в системе S' в точке с координатой

j

x

A

′

(принимающей значения –200 м, –100 м, 0 м, 100 м и 200 м для

разных часов) в системе S'. Событие B

k

(k =1, 2, 3, 4, 5) – фиксация

показания k-ых часов системы S, имеющих координату

k

x

B

(–200 м, –100 м, 0 м, 100 м и 200 м) в системе S в момент времени

0

B

=

′

k

t по часам системы S'. Обратим внимание на то, что все со-

бытия A

j

происходят в один и тот же момент времени в системе S.

И наоборот, все события B

j

происходят в один и тот же момент

времени в системе S'.

II. Пространственно-временные координаты событий A

j

и B

k

в системах S и S' связаны преобразованиями Лоренца (см. (5.3)),

полученными с учетом 0

A

=

j

t и 0

B

=

′

k

t :

jj

xx

AA

γ

=

′

,

jj

x

c

V

t

A

2

A

γ

−=

′

; (5.32)

kk

xx

BB

′

=

γ

,

kk

x

c

V

t

B

2

B

′

=

γ

. (5.33)

Здесь

j

t

A

′

– показания часов системы S',

j

x

A

– координата часов

системы S' в системе S,

k

t

B

– показания часов системы S,

k

x

B

′

– ко-

ордината часов системы S в системе S'.

Систему уравнений (5.32), (5.33) дополним выражением для

Лоренц-фактора:

()

2

/1

1

cV−

=

γ

. (5.34)

III. Решая полученную систему уравнений (5.32)

− (5.34) от-

носительно неизвестных пространственно-временных координат

(

j

t

A

′

,

j

x

A

и

k

t

B

,

k

x

B

′

) интересующих нас событий A и B и модуля

скорости

V движения системы отсчета S' относительно S, получим:

Русаков В.С. и др. Механика. Методика решения задач

Подождите немного. Документ загружается.