Русаков В.С. и др. Механика. Методика решения задач

Глава 4. Движение материальной точки в неинерциальных системах

131

другую – в меридиональной плоскости, в которой лежит вектор

начальной скорости пули

V (рис. 4.7). Будем считать, что поверх-

ность Земли является сферической, и Земля вместе со связанной с

ней системой отсчета X'Y'Z' вращается с постоянной угловой ско-

ростью

Т

π

ω

2

=

, где T = 24 ч.

На пулю в процессе полета действуют сила гравитационного

взаимодействия с Землей

гр

F

и силы инерции – центробежная сила

инерции

цб

F

и сила инерции Кориолиса

Кор

F

, изображенные на

рис. 4.7 в соответствии с (4.16) и (4.17). Отклонение пули от верти-

кальной черты мишени вызывает сила инерции Кориолиса.

Центробежная сила инерции имеет горизонтальную состав-

ляющую, и, следовательно, изменяет горизонтальную проекцию

скорости пули. Однако учет центробежной силы инерции даст ма-

лые поправки к величине и направлению скорости полета пули.

Сила инерции

Кориолиса не меняя величины скорости пули,

изменяет направление ее полета. При этом проекция скорости по-

лета пули на направление выстрела практически не меняется. По-

этому будем считать, что в первом приближении движение в гори-

зонтальном направлении происходит с постоянной скоростью, рав-

ной начальной скорости пули.

II. Время полета пули t находим

из условия равномерного

движения в направлении выстрела:

V

s

t

=

. (4.51)

Ускорение в восточном направлении, перпендикулярном на-

чальной скорости пули, определяется силой инерции Кориолиса

(см. рис. 4.7) и равно

ϕ

ω

sin2 Va

=

. (4.52)

Отклонение пули от вертикальной черты мишени при уско-

ренном движении в течение времени

τ

равно

2

at

l = . (4.53)

III. Решая полученную систему уравнений (4.51) – (4.53), на-

ходим искомое значение отклонения пули от вертикальной черты

мишени:

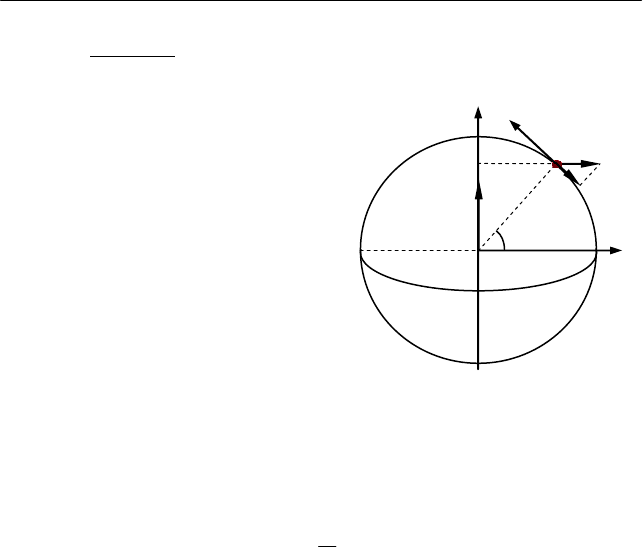
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

132

7

sin

2

≈=

V

s

l

ϕω

см. (4.54)

Оценим изменение горизон-

тальной проекции скорости пули

τ

VΔ под действием горизонтальной

составляющей центробежной силы

инерции

τ

цб

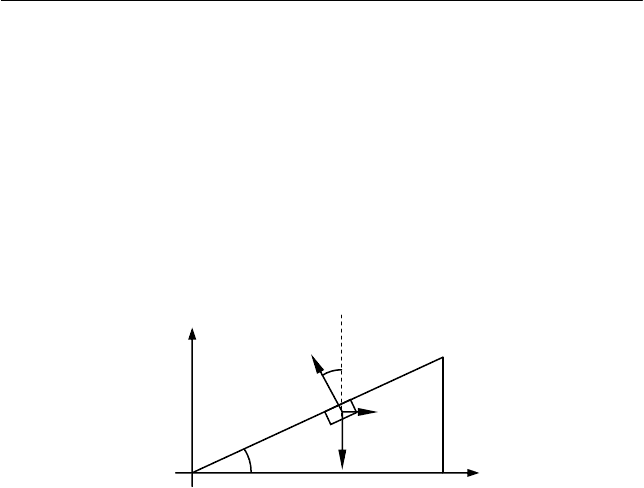
F . Запишем уравнение

движения пули в проекции на тан-

генциальную ось (см. рис. 4.8):

τ

цб

Fa =m . (4.55)

Используя (4.16) и (4.55), получаем

для горизонтальной проекции ус-

корения пули:

=−=

ϕω

τ

sin

2

ra

ϕϕω

sincos

2

R−= . (4.56)

Изменение горизонтальной проекции скорости пули под дей-

ствием центробежной силы инерции с учетом (4.51) равно:

V

s

RtaV

ϕϕω

ττ

sincosΔ

2

−=≅ . (4.57)

Подстановка численных значений заданных в условии задачи вели-

чин в (4.57) дает м/с900м/с01,0Δ

=

<

−

≅

VV

τ

, что подтверждает

справедливость принятого допущения.

Задача 4.6

(Вращающаяся неинерциальная система отсчета)

Вращение Земли вызывает отклонение поверхности воды в

реках от горизонтального положения. Определить, у какого берега

и на какую величину h уровень воды в реке будет выше. Река течет

в северном полушарии на широте

o

60=

ϕ

с севера на юг. Ширина

реки км1=L , скорость течения м/с1

=

V , период обращения Земли

вокруг своей оси ч24=T . Считать ускорение свободного падения

на данной широте равным

2

м/с8,9=g .

Рис. 4.8

ω

цб

F

φ

Z'

Y'

r

R

τ

цб

F

τ

Глава 4. Движение материальной точки в неинерциальных системах

133

Решение

I. Выделим мысленно небольшой объем жидкости вблизи по-

верхности и рассмотрим его движение в неинерциальной системе

отсчета, связанной с Землей. Направим ось Y вертикально вверх

(вдоль линии отвеса), а ось X – горизонтально, перпендикулярно

скорости течения реки в сторону правого берега (на запад).

На рис. 4.9 изображены силы, действующие на элемент объ-

ема жидкости – сила

тяжести mg , равнодействующая сил давления

со стороны всей остальной воды N и сила инерции Кориолиса

Кор

F .

Жидкость считаем несжимаемой, сил вязкого трения нет. На-

правление течения реки направлено за плоскость чертежа. Равно-

действующая сил давления направлена перпендикулярно поверх-

ности жидкости и образует угол

α

с вертикалью.

II. Жидкость движется в направлении, перпендикулярном

плоскости чертежа, следовательно, векторная сумма сил, лежащих

в плоскости чертежа и изображенных на рисунке, равна нулю:

0

Кор

=+

+

FNgm . (4.58)

Уравнение (4.58) в проекциях на оси выбранной системы ко-

ординат принимает вид:

.0cos

,0sin

Кор

=−

=+−

mgN

FN

α

(4.59)

Разность высот правого и левого берегов реки, как видно на

рис. 4.9, равна

α

tgLh

=

. (4.60)

Рис. 4.9

h

L

α

N

Кор

F

m

g

α

X

Y

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

134

Для силы инерции Кориолиса (см. (4.17)) в данном случае

справедливо выражение:

ϕ

ω

sin2

кор

VmF = . (4.61)

III. Решая систему уравнений (4.59) – (4.61), получаем, что

уровень воды у правого берега будет выше на величину

g

VL

h

ϕω

sin2

= . (4.62)

Подстановка численных значений заданных в условии задачи

величин в (4.62) дает искомое значение разности высот правого и

левого берегов см3.1≅h .

Задача 4.7

(Вращающаяся неинерциальная система отсчета)

Тонкий однородный стержень длиной L и массой m, шарнир-

но закрепленный в верхней точке О, вращается с постоянной угло-

вой скоростью

ω

вокруг вертикальной оси, проходящей через дан-

ную точку (см. рис. 4.10). Определить угол устойчивого вращения

стержня.

Решение

I. Задачу решаем в неинерциальной системе отсчета, связан-

ной со стержнем и вертикальной осью вращения. Будем считать

стержень абсолютно твердым телом. На стержень действуют три

силы: сила тяжести mg, сила реакции со стороны шарнира и цен-

тробежная сила инерции. Силой сопротивления воздуха пренебре-

гаем. Под действием силы тяжести и силы

реакции

со стороны шарнира стержень со-

вершает вращательное движение относи-

тельно лабораторной инерциальной систе-

мы отсчета, причем различные участки

стержня движутся по окружностям разных

радиусов. Следовательно, различна и сила

инерции

ин

dF , действующая на отдельные

элементы стержня в неинерциальной сис-

теме отсчета.

II. При устойчивом вращении стер-

жень отклонен от вертикальной оси на по-

стоянный угол

α

. Поскольку стержень по-

Рис. 4.10

α

ω

O

dl

ин

dF

mg

Глава 4. Движение материальной точки в неинерциальных системах

135

коится в выбранной неинерциальной системе отсчета, сумма мо-

ментов всех сил, действующих на стержень в этой системе, относи-

тельно горизонтальной оси, проходящей через точку О перпенди-

кулярно плоскости чертежа (рис. 4.10) и направленной из плоско-

сти чертежа, равна нулю:

0

ин

=+ MM

mg

. (4.63)

При записи (4.63) учтено, что момент силы реакции шарнира отно-

сительно указанной оси равен нулю.

Запишем выражение для момента силы тяжести:

α

sin

2

L

mgM

mg

−= . (4.64)

Для нахождения суммарного момента сил инерции рассмот-

рим элемент стержня длиной dl, находящийся на расстоянии l от

точки О. Центробежная сила инерции (см. (4.16)), действующая на

этот элемент, равна

rlSF

2

ин

dd

ωρ

= , (4.65)

где

ρ

– плотность стержня, S – площадь его поперечного сечения,

r – расстояние от элемента стержня до оси вращения.

Момент силы инерции относительно горизонтальной оси

можно записать в виде:

ααωρα

cossindcosdd

2

инин

lllSlFM == . (4.66)

Суммарный момент сил инерции равен

===

∫∫

L

llSMM

0

22

инин

dcossind

ααωρ

ααω

cossin

3

1

22

mL= . (4.67)

III. Решая полученную систему уравнений (4.63), (4.64) и

(4.67) относительно угла

α

, получаем:

2

3

cos

ω

α

L

g

= , (4.68)

0sin =

α

. (4.69)

Нетрудно видеть, что при

L

g

2

3

>

ω

значение угла

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

136

⎟

⎠

⎞

⎜

⎝

⎛

=

2

3

arccos

ω

α

L

g

(4.70)

соответствует устойчивому вращению стержня, а значение

α

= 0,

которое следует из уравнения (4.69), соответствует неустойчивому

вращению стержня. В случае

L

g

2

3

≤

ω

устойчивым является вер-

тикальное положение стержня (

α

= 0).

Задача 4.8

(Вращающаяся неинерциальная система отсчета)

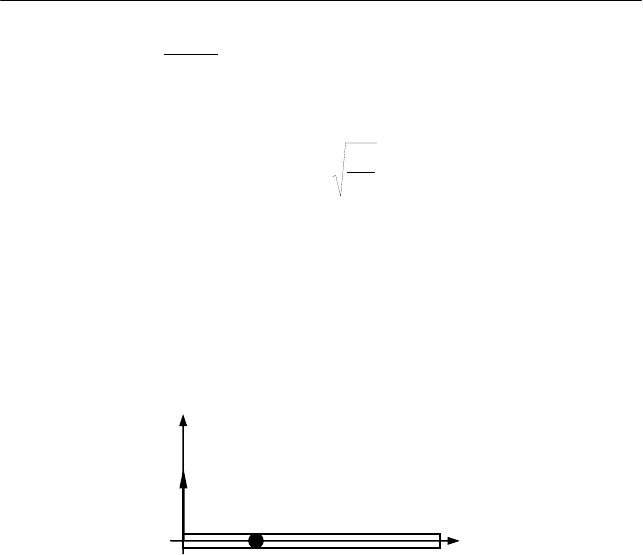
Гладкая горизонтальная трубка длиной

L равномерно враща-

ется с угловой скоростью

ω вокруг вертикальной оси, проходящей

через один из ее концов (см. рис. 4.11).

Определить, за какое время

t

0

маленький шарик, находящий-

ся на расстоянии

l от оси трубки, достигнет ее конца, а также мо-

дуль скорости шарика относительно земли

0

υ

в момент его вылета

из трубки. Начальную скорость шарика относительно трубки при-

нять равной нулю.

Решение

I. Задачу решаем в неинерциальной системе отсчета, связан-

ной с трубкой и вертикальной осью вращения. Оси X' и Y' правой

системы координат X'Y'Z' направим вдоль трубки и угловой скоро-

сти ее вращения соответственно (см. рис. 4.11). Шарик считаем ма-

териальной точкой, а трубку – абсолютно твердым телом. На ша-

рик в процессе движения действуют четыре силы:

сила тяжести mg,

сила реакции трубки, центробежная сила инерции, а также сила

инерции Кориолиса. Силами трения и сопротивления воздуха пре-

Рис. 4.11

ω

r

'

O

X'

Y'

Глава 4. Движение материальной точки в неинерциальных системах

137

небрегаем. Шарик движется вдоль трубки, причем его ускорение

относительно неинерциальной системы отсчета определяется толь-

ко центробежной силой инерции, поскольку направление действия

остальных сил перпендикулярно его движению.

II. Запишем уравнение движения шарика относительно вы-

бранной неинерциальной системы отсчета в проекции на ось, сов-

падающую с геометрической осью трубки (см. рис. 4.11):

''

2

rmma

ω

= . (4.71)

С целью упрощения дальнейшего интегрирования уравнения

(4.71) выразим проекцию ускорения шарика

a' через производную

проекции скорости по пространственной координате

r' шарика:

'

'd

d

'd

d

'd

'

υ

υυυ

rt

r

rt

a =⋅==

. (4.72)

III. Используя соотношение (4.72), исключаем проекцию ус-

корения из уравнения движения шарика (4.71):

'

'd

'

2

r

ω

υ

= . (4.73)

Полученное уравнение (4.73) решаем методом разделения

переменных:

'd''d'

'

2

'

0

rr

r

l

∫∫

=

ωυυ

υ

. (4.74)

Интегрируя (4.74), получаем связь проекции скорости шари-

ка

'

υ

и его координаты r':

22

'' lr −=

ωυ

. (4.75)

Следовательно

22

'

d

'd

lr

t

r

−=

ω

. (4.76)

Уравнение (4.76) решаем методом разделения переменных:

∫∫

=

−

0

22

d

'

'd

t

L

l

t

lr

r

ω

. (4.77)

В результате интегрирования уравнения (4.77) находим ис-

комое время движения шарика в трубке:

⎟

⎠

⎞

⎜

⎝

⎛

−+= 1ln

1

2

0

l

L

l

L

t

ω

. (4.78)

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

138

Для нахождения скорости шарика относительно трубки вос-

пользуемся (4.75):

'X

22

'' eυ ⋅−= lr

ω

, (4.79)

где

'X

e − единичный вектор вдоль оси X'.

Скорость шарика относительно лабораторной инерциальной

системы отсчета в соответствии с (4.8) может быть записана в виде:

[

]

'X

22

'Z

'' eeυrωυ ⋅−+−=

′

+

′

= lrr

ωω

, (4.80)

где

'Z

e − единичный вектор вдоль оси Z'. Следовательно, искомый

модуль скорости шарика относительно лабораторной системы от-

счета равен:

22

'2 lr −=

ωυ

. (4.81)

Задача 4.9

1

(Поступательно движущаяся неинерциальная система отсчета)

Однородный цилиндр массой m скатывается без проскальзы-

вания с клина массой M и углом при основании

α

, стоящего на

гладкой горизонтальной поверхности. Найти ускорение клина.

Решение

I. Задачу решаем в неинерциальной системе отсчета, связан-

ной с клином, оси которой X' и Y' направим вдоль горизонтальной

и вертикальной поверхностей клина соответственно (см. рис. 4.12 и

4.13).

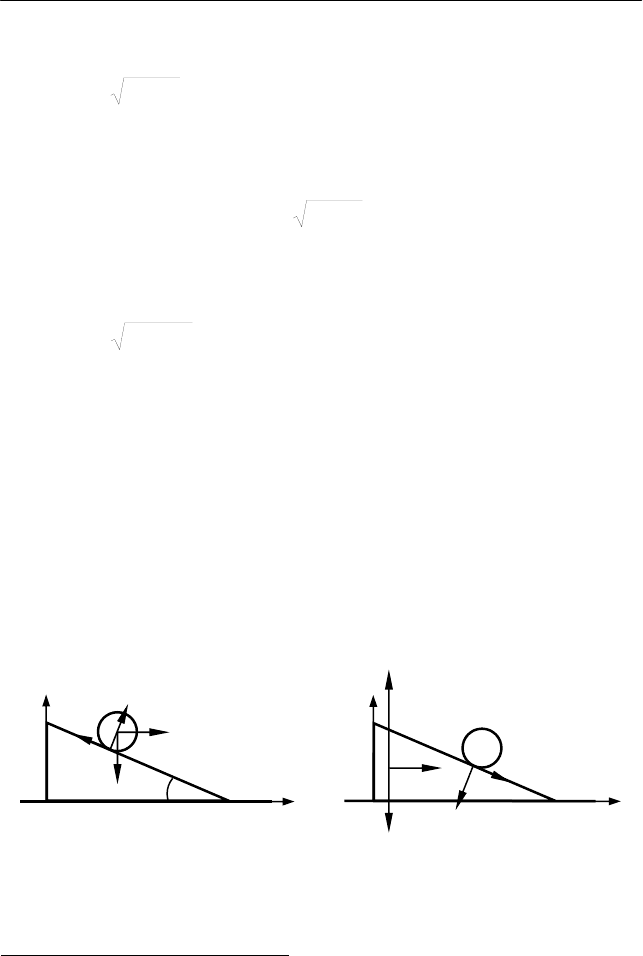
На цилиндр действуют четыре силы: сила тяжести mg, сила

трения покоя F

тр

(качение происходит без проскальзывания) и сила

1

Задачи 4.9 и 4.10, а также задачу 2 для самостоятельного решения реко-

мендуем решать после ознакомления с содержанием Главы 6.

Рис. 4.12 Рис. 4.13

X'

Y'

α

0

am−

N

F

т

р

mg

Mg

X'

Y'

R

F

тр

N

0

aM

−

Глава 4. Движение материальной точки в неинерциальных системах

139

нормальной реакции N со стороны клина, а также переносная сила

инерции

0

am

−

(рис. 4.12), обусловленная движением клина отно-

сительно лабораторной инерциальной системы отсчета с ускорени-

ем

0

a , направленным в отрицательном направлении оси X'. Силой

сопротивления воздуха пренебрегаем.

На клин действуют: сила тяжести Mg, силы нормального

давления N и трения покоя F

тр

со стороны цилиндра, сила нормаль-

ной реакции опоры R и переносная сила инерции

0

aM

−

(рис. 4.13).

II. Запишем уравнение движения центра масс цилиндра в

проекциях на оси выбранной системы координат:

0тр'

cossin maFNma

x

+

−=

α

, (4.82)

mgFNma

y

−

+=

α

sincos

тр'

, (4.83)

где

'x

a ,

'y

a – проекции ускорения a центра масс цилиндра, для ко-

торых можно записать:

α

cos

'

aa

x

=

,

α

sin

'

aa

y

−

= . (4.84)

Уравнение вращательного движения (см. (6.30) в Главе 6)

цилиндра относительно оси, совпадающей с его осью и направлен-

ной за плоскость чертежа (см. рис. 4.12), имеет вид:

rF

mr

тр

2

=

ϕ

&&

, (4.85)

где

ϕ

&&

– угловое ускорение цилиндра, r – его радиус. При записи

(4.85) учтено известное выражение для момента инерции J цилинд-

ра относительно оси, совпадающей с осью цилиндра –

2

mr

J = , а

также равенство нулю моментов сил инерции, нормальной реакции

и тяжести относительно указанной оси.

Из условия качения без проскальзывания получаем уравне-

ние связи ускорения оси цилиндра (совпадающего с ускорением

центра масс a) с его угловым ускорением:

ra

ϕ

&&

=

. (4.86)

Запишем также уравнение движения клина в проекции на ось

Х':

0тр

cossin0 MaFN

+

−

=

α

. (4.87)

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

140

III. Решая совместно уравнения (4.82) – (4.87), получаем вы-

ражение для модуля ускорения клина:

)sin21(3

2sin

2

0

α

++

=

mM

mg

a . (4.88)

Следовательно, искомое ускорение клина относительно лаборатор-

ной инерциальной системы отсчета равно:

X

2

0

)sin21(3

2sin

ea

α

++

−=

mM

mg

, (4.89)

где

X

e − единичный вектор лабораторной инерциальной системы

отсчета, совпадающий с направлением оси X' неинерциальной сис-

темы отсчета.

Задача 4.10

(Поступательно движущаяся неинерциальная система отсчета)

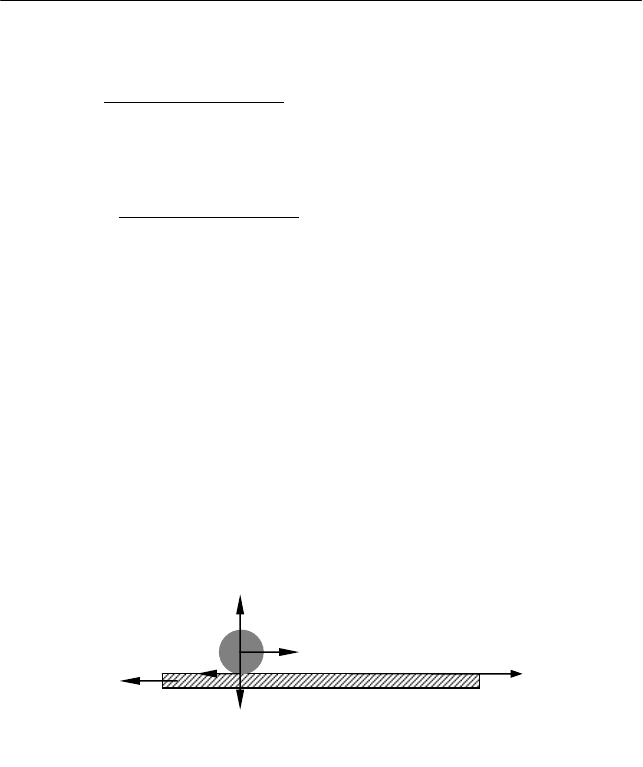
Цилиндр массой m и радиусом R находится на расстоянии L

от правого края доски. Доска начинает двигаться с ускорением

a

влево (рис. 4.14), при этом цилиндр катится по доске без проскаль-

зывания. С какой скоростью

цм

V относительно доски будет дви-

гаться центр масс цилиндра в тот момент, когда он будет находить-

ся над краем доски?

Решение

I. Задачу решаем в неинерциальной системе отсчета, связан-

ной с доской. Направим ось X' системы координат противоположно

ускорению доски. На цилиндр в процессе движения действуют че-

тыре силы: сила тяжести

g

m , сила нормальной реакции опоры

N

,

сила трения покоя

тр

F (проскальзывания при качении нет) и пере-

носная сила инерции

am− . Силой сопротивления воздуха пренеб-

регаем.

Рис. 4.14

a

X'

mg

N

am

−

тр

F

Русаков В.С. и др. Механика. Методика решения задач

Подождите немного. Документ загружается.