Русаков В.С. и др. Механика. Методика решения задач
Подождите немного. Документ загружается.

Глава 3. Законы изменения импульса и механической энергии
111
Общая масса шариков равна массе поршня. Во сколько раз изме-
нится расстояние между равновесным положением поршня и дном
цилиндра, если массу поршня увеличить в два раза? Считать моду-
ли скоростей шариков у дна цилиндра одинаковыми.
Решение
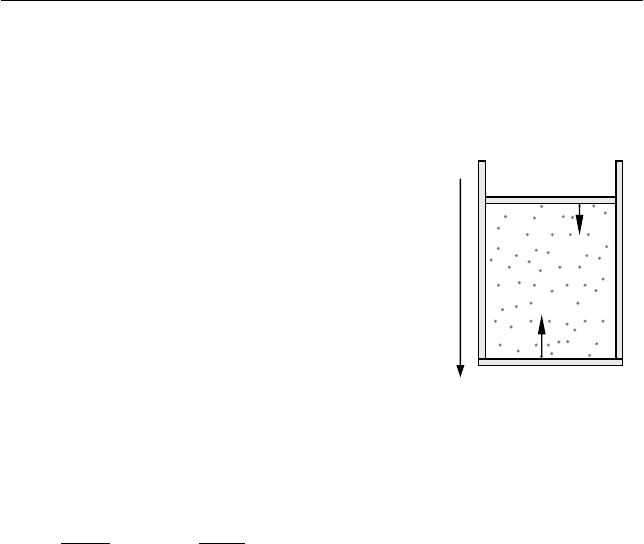
I. Направим ось X декартовой сис-
темы координат, жестко связанной с ци-
линдром, вертикально вниз (см.
рис. 3.21). Будем считать в соответствии с
условием, что маленьких шариков на-
столько много, что дрожанием поршня в
результате соударений с шариками мож-
но пренебречь. Поскольку шарики малы,
не будем учитывать соударения между
ними.
II. Запишем закон сохранения
меха-
нической энергии произвольного шарика на интервале времени
между последовательными его соударениями с дном цилиндра и
поршнем:
22
2
1
2
0
υυ
m
mgH
m
+= . (3.121)
где
υ
0
и
υ
1
– модули скоростей шарика у дна цилиндра и поверхно-
сти поршня соответственно, H – расстояние между дном цилиндра
и поршнем.
В результате соударения с поршнем проекция импульса ша-
рика на ось X изменяется на величину
1
2Δ
υ
mp
=
. (3.122)
За время t
0
между двумя последовательными ударами произ-
вольного шарика о поршень произойдет N соударений всех шари-
ков с поршнем. Изменение импульса механической системы, со-
стоящей из N шариков, за время t
0
равно импульсу средней на дан-
ном интервале времени силы F, действующей на поршень со сто-
роны шариков:
0
Δ FtpN = . (3.123)
В соответствии со вторым законом Ньютона запишем усло-
вие равновесия поршня:
0=
−
FMg . (3.124)
Рис. 3.21
X
υ
0
υ
1
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
112
Поскольку в поле сил тяжести Земли движение шариков про-
исходит с постоянным ускорением
g, модули скоростей произволь-
ного шарика у дна цилиндра и поверхности поршня связаны соот-
ношением:
2
0
10
t
g+=
υυ
. (3.125)
III. Решим систему уравнений (3.121) – (3.125) относительно
расстояния H между дном цилиндра и поршнем:
2
2
0
)(
)2(
2
MmNg
mNMmN
H
+
+
⋅=
υ
. (3.126)
При увеличении массы поршня в два раза расстояние H
2
ме-
жду дном цилиндра и поршнем, находящимся в новом равновесном
состоянии, становится равным:
2
2
0
2
)2(
)4(
2
MmNg
mNMmN
H
+
+
⋅=
υ
. (3.127)
Следовательно, при увеличении массы поршня расстояние
между равновесным положением поршня и дном цилиндра изме-
нится в k раз:
3
2
2
)2(
))(4(
MmN
MmNMmN
H
H
k
+
++
== . (3.128)
Учитывая, что по условию задачи mN = M, окончательно по-
лучим:
27
20
=k . (3.129)
3.4. Задачи для самостоятельного решения
Задача 1
Три лодки одинаковой массой m идут в кильватер (друг за
другом) с одинаковой скоростью
υ
. Из средней лодки одновре-
менно в переднюю и заднюю лодки бросают со скоростью u отно-
сительно лодки грузы массой m
1
. Каковы будут скорости лодок по-
сле переброски грузов? Изменением импульса и механической
энергии воды, а также силами трения пренебречь.
Ответ:
u
mm
m
1
1
1
+
+=
υυ
,
υ
υ
=
2
, u
mm
m
1
1
3
+
−=
υυ
.

Глава 3. Законы изменения импульса и механической энергии
113
Задача 2
На гладкой горизонтальной поверхности лежат два одинако-
вых шарика массами m
0
, соединенные невесомой пружинкой жест-
костью k и длиной l
0
в недеформированном состоянии. В один из
шариков попадает летящая горизонтально вдоль оси пружины со
скоростью
υ
пуля массой m и застревает в нем. Найти максималь-
ное и минимальное расстояние между шариками в процессе их
движения.
Ответ: l
max
= l
0
+ Δl, l
min
= l
0
– Δl, где
kmmmm
m
ml
)2)((
Δ
00
0
++
=
υ
.
Задача 3
С концов платформы массой М и длиной l, которая может
перемещаться без трения, навстречу друг другу бегут два зайца
массами m и 2m с постоянными относительно платформы скоро-
стями. Второй заяц (массой 2m) бежит в два раза быстрее первого.
На сколько сместится платформа, когда второй заяц добежит до ее
конца?
Ответ
:
()
l
Mm
m
x
+
=
32
3
.
Задача 4
На нити, прикрепленной к воздушному шару массой M, сво-
бодно висящему в воздухе, сидит жук массой m, который начинает
двигаться с постоянной относительно нити скоростью
U вверх. Оп-
ределить скорости шара и жука относительно Земли.
Ответ:
Uυ
Mm
m
+
−=
ш
, Uυ
Mm
M
+
=
ж
.
Задача 5
На неподвижной тележке находятся два человека. В каком
случае тележка приобретет большую скорость: если люди спрыг-
нут с тележки одновременно или друг за другом в одном направле-
нии?
Ответ:
тележка приобретет большую скорость, если люди спрыг-
нут друг за другом.
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
114
Задача 6
Три упругих шара одинакового радиуса с массами m
1
, m
2
и m
3
находятся на одной прямой. Двигаясь с некоторой скоростью, пер-
вый шар массой m
1
испытывает центральное соударение cо вторым
покоящимся шаром массой m
2
. Чему должна быть равна масса вто-
рого шара, чтобы после его соударения с третьим покоящимся ша-
ром скорость последнего была максимальной?
Ответ:
312
mmm = .
Задача 7
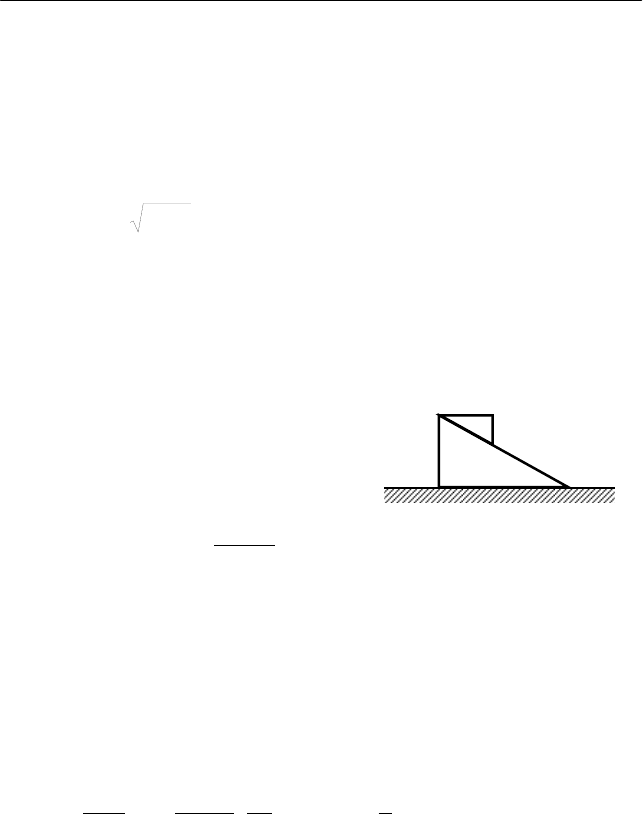
На горизонтальной поверхности лежит клин массой M с дли-
ной основания a. Второй клин массой m и длиной основания b < a
начинает соскальзывать с поверхности нижнего клина из положе-
ния, изображенного на рисунке. На
какое расстояние и в какую сторону
переместится нижний клин к моменту
касания верхним клином горизон-
тальной поверхности
? Силами трения
пренебречь.
Ответ: влево на
)(Δ ba
Mm
m
x −
+
= .
Задача 8
Частица массой m испытала столкновение с покоящейся час-
тицей массой М, в результате которого первая частица отклонилась
на угол π/2, а вторая частица стала двигаться в направлении, со-
ставляющим угол
α
= 30° с первоначальным направлением движе-
ния налетающей частицы. Как изменилась кинетическая энергия
системы этих двух частиц после столкновения, если M/m = 5?
Ответ:
5
2
sin
cos
1
1
Δ
2
2k
0
k
=
⎥
⎦
⎤
⎢
⎣
⎡
+−=
α
α
M
m
E
E
.
Задача 9
Частица массой m
1
испытала абсолютно упругое центральное
столкновение с покоящейся частицей массой m
2
. Определить отно-
сительное изменение кинетической энергии налетающей частицы.
b
a
M
m

Глава 3. Законы изменения импульса и механической энергии
115
Ответ:
()
2
21
21
k
0
k
4Δ
mm
mm
E
E
+
= .
Задача 10
Частица массой m
1
испытала абсолютно упругое столкнове-
ние с покоящейся частицей массой m
2
. Определить относительное
изменение кинетической энергии налетающей частицы, если в ре-
зультате столкновения она отскочила под прямым углом к своему
первоначальному направлению движения.
Ответ:
21
1
k
0
k
2Δ
mm
m
E
E
+
= .
Задача 11
После абсолютно упругого столкновения частицы массой m
1
с покоящейся частицей массой m
2
обе частицы разлетелись сим-
метрично относительно направления первоначального движения
первой частицы, и угол между их направлениями разлета
α
= 60°.
Найти отношение масс этих частиц.
Ответ:
2
2
1
=
m
m
.
Задача 12
При бомбардировке атомов гелия α-частицами с энергией
МэВ1
0α
=E найдено, что налетающая частица отклонилась на угол
°= 60
ϕ
по отношению к первоначальному направлению полета.
Считая удар абсолютно упругим, определить энергию атома гелия
He
E и
α
-частицы
α
E после соударения.
Ответ: МэВ75,0sin
2
α0He
==
ϕ
EE , МэВ25,0cos
2
α0α
==
ϕ
EE .
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
116
ГЛАВА 4
ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ В НЕИНЕРЦИАЛЬ-
НЫХ СИСТЕМАХ ОТСЧЕТА. СИЛЫ ИНЕРЦИИ
4.1. Теоретический материал
Рассмотрим две системы отсчета S и S', движущиеся произ-
вольно друг относительно друга. Зададим движение системы от-
счета S' относительно системы S зависимостями от времени ради-
ус-вектора
)(tR начала системы отсчета S' и угловой скорости
вращения )(tω системы S' вокруг своего начала отсчета (рис. 4.1).
Физически бесконечно малый поворот системы отсчета S' (в
том числе и тела отсчета) описывается вектором
d
α
(рис. 4.2). На-
правление этого вектора совпадает с осью поворота и согласно
правилу буравчика задает направление поворота, а его модуль
d
α
≡ ⎪d
α
⎪ равен углу поворота.
Найдем скорость изменения произвольного вектора
c , жест-
ко связанного с телом отсчета системы S'. В соответствии с рис. 4.2
модуль изменения вектора
c равен:
γα
sindd ⋅⋅= cc , (4.1)
следовательно
[]
cc ,d αd
=
(4.2)
и
Рис. 4.1. Взаимная ориентация осей
координат произвольно
движущихся систем отсчета
S и S'.
S
)(tr
O
)(tr
′
)(tR
)(tω
S'
O'
M
Рис. 4.2. Изменение произволь-
ного вектора
c
, жестко
связанного с телом от-
счета системы S'.
γ
d
α
d
α
c
cd
O'

Глава 4. Движение материальной точки в неинерциальных системах
117
[]
ωcc
α
c ≡
⎥
⎦
⎤
⎢
⎣
⎡
=
td
d
&
, (4.3)
где
td
α
ω
d
≡ – угловая скорость вращения.
Запишем радиус-вектор )(tr произвольной материальной
точки M относительно системы S через радиус-вектор )(tR начала
системы отсчета S' относительно системы S и радиус-вектор
)(tr
′
материальной точки M относительно системы
S
′
(рис. 4.1):
)()()( ttt rRr
′
+=
. (4.4)
Продифференцируем обе части уравнения (4.4) по времени
при постоянных ортах системы S. В соответствии с определением
скорости и ускорения материальной точки (см. Главу 1), а также
угловой скорости вращения системы отсчета, получим:
(
)
=
∂
′′
+
′′
+
′′
∂
+=
′
+==
S
S
S
S
t
zyx kji
VrRrυ
&
&
&
()
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
′
∂
′
+
∂
′
∂
′
+
∂
′
∂
′
+
′′
+
′′
+
′′
+=
SSS
S'S'S'
t
z
t
y
t
xzyx
kji
kjiV
&
&&
[]
[
]
[
]
()
=
′
′
+
′
′
+
′′
+
′
+
=
kωjωiωυV zyx
[
]
rωυV
′
+
′
+
, (4.5)
[
]
=
∂
′
∂
+
′
+==
S
S
S
S
t
rω
υVυa
&
&
&
[]
[
]
[
]
[
]
=
′
+
′
+
′
+
′
+
′
+
=
rωυωrωυωaA ,
&
[]
[
]
[
]
[
]
rωωrωυωaA
′
+
′
+
′
+
′
+
=
&
2 . (4.6)
Здесь нижние индексы S и S' означают дифференцирование при
постоянных ортах систем S и
S
′
соответственно, V – скорость и A
– ускорение начала отсчета системы
S
′
относительно S.
В результате мы получили взаимосвязь (формулы сложения)
радиус-векторов )(
tr и
)(tr
′
, скоростей )(tυ и
)(tυ
′
, а также уско-
рений )(
ta и
)(ta
′
материальной точки относительно двух произ-
вольно движущихся относительно друг друга систем отсчета S и S':
r
R
r
′
+
=
, (4.7)
[]
{
υυυrωVυ
′
+
=
′
+
′
+
=
пер
наяотноситель
переносная
43421
, (4.8)

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
118
[]
[
]
[
]
[
]
{
=
′
+
′
+
′
+
′
+
=
ноеотноситель
Кориолиса
переносное
мительноецентростре
2 aυωrωωrωAa
321
44443444421
43421
&
aaa
′
++
=
Корпер
. (4.9)
Здесь
[]
rωVυ
′
+=
пер
– переносная и υ
′
– относительная скорости
движения материальной точки;
[
]
υωa
′
=
2
Кор
– ускорение Корио-
лиса
,
[][]
rωωa
′
=
цс
– центростремительное,
[] [][]
rωωrωAa
′
+
′
+
=
&
пер
– переносное и a
′
– относительное уско-
рения материальной точки.
Если материальная точка покоится относительно системы S',
то
r
R
r
′
+
=
, (4.10)
[]
43421
переносная
пер
rωVυυ
′
+=
=
, (4.11)
[]
[
]
[
]
44443444421
43421
&
переносное
мительноецентростре
пер
rωωrωAaa
′
+
′
+=
=
(4.12)
Уравнение движения материальной точки относительно
неинерциальной системы отсчета
Пусть система отсчета S является инерциальной (см. Гла-
ву 2). Запишем уравнение движения материальной точки M, на ко-
торую действуют силы
i
F , относительно системы отсчета S – 2-ой
закон Ньютона:
∑
=
i
i
m Fa . (4.13)
Подставим в уравнение (4.13) полученное выражение (4.9)
для ускорения материальной точки относительно произвольно
движущейся системы отсчета S' и несколько его преобразуем:
[]
[
][]
[
]
∑
=
′
+
′
+
′
+
′
+
i
i
mmmmm FaυωrωωrωA 2
&
,
[
]
[
]
[
]
[
]
43421
44443444421
43421
&
Кориолиса
переносная
аяцентробежн
2 υωrωωrωAFa
′
−
′
−
′
−−=
′
∑
mmmmm
i
i
, (4.14)

Глава 4. Движение материальной точки в неинерциальных системах
119
Корпер
FFFa ++=
′
∑
i
i
m . (4.15)
В результате мы получили уравнение движения материаль-
ной точки относительно в общем случае неинерциальной системы
отсчета S'. Как видим, в неинерциальной системе отсчета также
можно использовать второй закон Ньютона, если к "материаль-
ным" силам, действующим на материальную точку со стороны ма-
териальных тел, добавить так называемые
силы инерции:
переносную –
[]
[
]
[
]
[
]
цб
аяцентробежн
пер
FrωArωωrωAF
+
′
−
−
=
′
−
′
−−=
&
43421
&
mmmmm , (4.16)
Кориолиса –
[]
υωF
′
−= m2
Кор
. (4.17)
Заметим, что силы инерции вызваны не взаимодействием ма-
териальных объектов, а выбором неинерциальной системы отсчета,
относительно которой рассматривается движение тел. В отличие от
"материальных" сил для сил инерции нельзя указать тела, со сторо-
ны которых они действуют, следовательно, к ним не применим
третий закон Ньютона (см. Главу 2).
Переносная сила инерции
связана как с ускоренным движе-
нием начала системы отсчета S', так и с вращением этой системы
относительно инерциальной системы отсчета. Сила Кориолиса воз-
никает только при движении материальной точки относительно
вращающейся неинерциальной системы отсчета S'.
Любую задачу можно решать как в инерциальной, так и в не-
инерциальной системах отсчета, пользуясь либо уравнениями
дви-
жения, либо законами сохранения (см. Главу 3). При этом необхо-
димо учитывать силы инерции, их импульс и работу точно так же,
как и для "материальных" сил – сил взаимодействия материальных
объектов.
4.2. Основные типы задач и методы их решения
4.2.1. Классификация задач
Большинство задач на движение тел в неинерциальных сис-
темах отсчета можно условно отнести к следующим типам задач
или их комбинациям. Задачи на движение тел в:

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
120
1) поступательно движущейся неинерциальной системе от-
счета,
2) вращающейся неинерциальной системе отсчета.
4.2.2. Общая схема решения задач механики в
неинерциальных системах отсчета с использованием
законов Ньютона
I.
Определиться с моделями материальных объектов и явле-
ний.
1. Нарисовать чертеж, на котором изобразить рассматривае-
мые тела.
2. Выбрать неинерциальную систему отсчета и изобразить на
чертеже ее систему координат (из соображений удобства).
3. Изобразить и обозначить все силы, в том числе и силы
инерции, а также необходимые кинематические характе-
ристики системы.
4. Выбрать модели тел и их движения (если это
не сделано в
условии задачи).
II. Записать полную систему уравнений для искомых величин.
1. Записать уравнения движения в проекциях на оси коорди-
нат выбранной неинерциальной системы отсчета для всех
тел системы.
2. Использовать третий закон Ньютона для материальных
сил, если это не было сделано ранее в п. 3.
3. Использовать законы, описывающие индивидуальные
свойства сил.
4. Записать уравнения кинематической связи.
5. Использовать результаты ранее решенных задач и
особые
условия задачи.
III. Получить искомый результат в аналитическом и числен-
ном видах.
1. Решить систему полученных уравнений.
2. Провести анализ решения (проверить размерность и лиш-
ние корни, рассмотреть характерные случаи, установить
область применимости).
3. Получить численный результат.
