Русаков В.С. и др. Механика. Методика решения задач

Глава 7. Законы сохранения момента импульса и механической энергии

241

ний длин и масс, расположенная выше изображенной кривой, соот-

ветствует случаю соударения стержня с потолком.

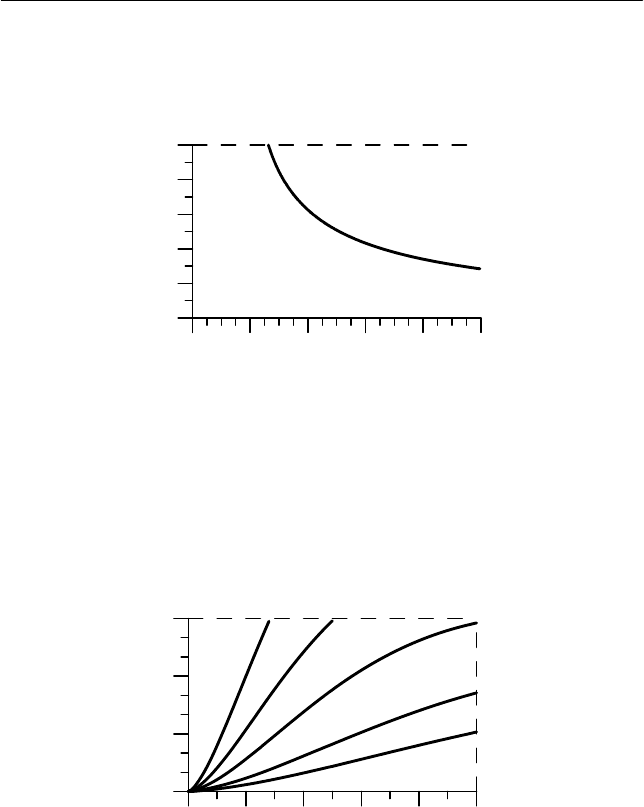
На рис. 7.4 изображены зависимости максимального угла от-

клонения стержня после соударения от отношения длин маятника и

стержня

()

Ll /

max

α

при различных значениях отношения их масс

)/( Mm .

Как видим, при увеличении отношения длин маятника и

стержня максимальный угол отклонения стержня возрастает, при-

0 0.4 0.8 1.2 1.

6

2

0

0.2

0.4

0.6

0.8

1

l/L

m/M

2/

max

π

α

=

2/

max

π

α

<

Рис. 7.3

Рис. 7.4

00.20.40.

6

0.8 1

0

30

60

90

l/L

m/M = 2 1

0,5

0,3

0,1

°,

max

α

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

242

чем скорость возрастания увеличивается с увеличением отношения

масс маятника и стержня.

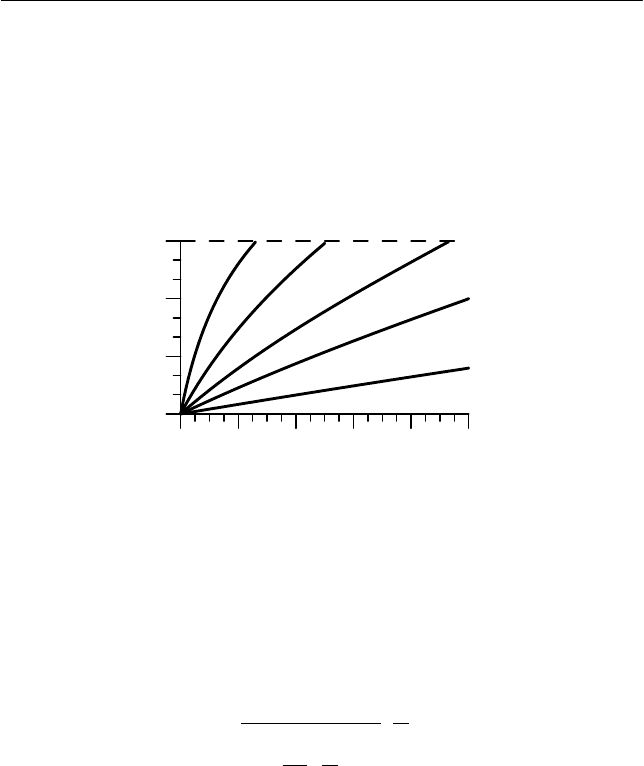
На рис. 7.5 изображены зависимости максимального угла от-

клонения стержня после соударения от отношения масс маятника и

стержня

()

Mm /

max

α

при различных значениях отношения их длин

)/( Ll .

Как видим, при увеличении отношения масс маятника и

стержня максимальный угол отклонения стержня возрастает, при-

чем скорость возрастания увеличивается с увеличением отношения

длин маятника и стержня.

Ответ:

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+

−=

l

L

l

L

m

M

2

max

3

24

1arccos

α

.

Задача 7.2

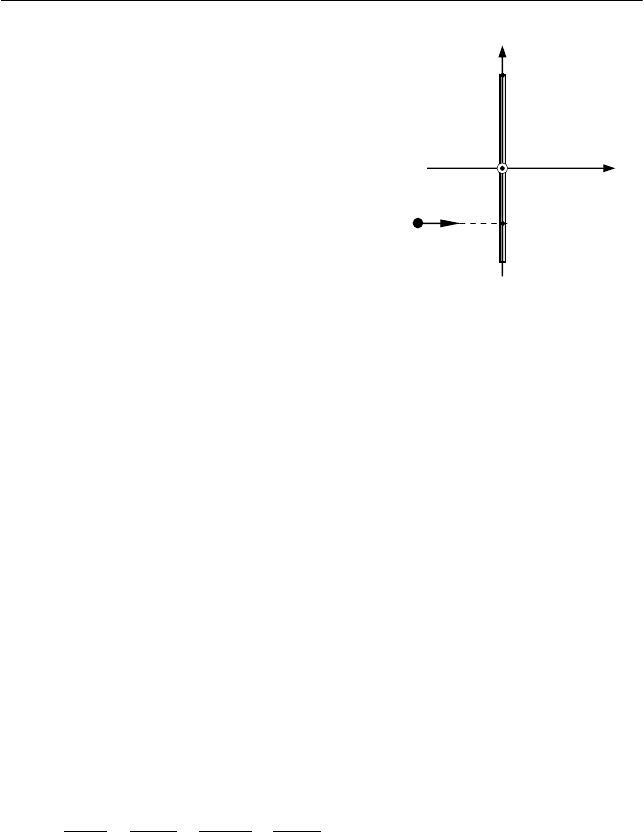
На гладкой горизонтальной поверхности лежат небольшая

шайба массой m и тонкий однородный стержень длиной L и массой

M. Шайбе сообщили скорость

υ

в горизонтальном направлении

перпендикулярно стержню (см. рис. 7.6). Шайба абсолютно упруго

соударяется со стержнем в точке B на расстоянии l от его центра

(точка O). Определить это расстояние в трех случаях:

m/M

l/L = 1

0,5

°,

max

α

0 0.4 0.8 1.2 1.

6

2

0

30

60

90

0,3

0,2

0,1

Рис. 7.5

Глава 7. Законы сохранения момента импульса и механической энергии

243

1) сразу после соударения шайба

останавливается,

2) шайба передает стержню мак-

симальный импульс,

3) скорость конца стержня (точка

A на рис. 7.6) после соударения равна

нулю.

Решение

I. Задачу решаем относительно ла-

бораторной инерциальной системы от-

счета. Поскольку соударение шайбы со

стержнем является абсолютно упругим, а

на систему тел «стержень + шайба» не действуют внешние силы

вдоль горизонтальной поверхности, то выполняются все три закона

сохранения: закон сохранения импульса, закон сохранения момента

импульса и закон сохранения механической энергии. Выберем сис

-

тему координат так, как показано на рис. 7.6. Ось, относительно

которой будем рассматривать вращение, удобно взять проходящей

через центр стержня перпендикулярно горизонтальной поверхно-

сти и направленной из плоскости чертежа.

II. Запишем три закона сохранения для выбранной системы

тел для интервала времени до соударения – сразу после соударе-

ния.

Закон сохранения проекции импульса на

ось X выбранной

системы координат:

υ

′′

+

′

= Mmm

. (7.34)

Закон сохранения момента импульса относительно выбран-

ной оси:

ω

υ

0

Jlmlm +

′

=

. (7.35)

Закон сохранения механической энергии:

2222

2

0

222

ωυυυ

JMmm

+

′′

+

′

= . (7.36)

Здесь

υ

′

,

υ

′′

– проекции скоростей шайбы и центра стержня на ось

X сразу после соударения (проекции скоростей на ось Y в этот мо-

мент времени равны нулю),

ω

– угловая скорость вращения стерж-

ня в тот же момент времени.

Рис. 7.6

A

O

B

X

Y

υ

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

244

Момент инерции стержня относительно оси, проходящей че-

рез его центр масс, равен (6.43):

2

0

12

1

MLJ

= . (7.37)

В соответствии с принципом суперпозиции движений (см.

(1.26) в Главе 1) скорость

A

υ

точки А стержня складывается из

скорости центра масс и скорости вращательного движения этой

точки вокруг оси, проходящей через центр масс:

2

A

L

ωυυ

−

′′

=

. (7.38)

III. Решение системы уравнений (7.34) – (7.38) относительно

искомых величин имеет вид:

2

0

2

0

)(

MmlJMm

++

+−

=

′

υυ

, (7.39)

2

0

)(

2

MmlJMm

MJ

M

m

++

⋅=

′′

υυ

, (7.40)

2

0

)(

2

MmlJMm

MJ

J

ml

++

⋅=

υω

, (7.41)

⎟

⎠

⎞

⎜

⎝

⎛

−

++

=

0

2

0

A

2

1

)(

2

J

lL

M

MmlJMm

mMJ

υ

. (7.42)

Расстояние l от точки соударения до начала координат, при

котором шайба остановится после удара, найдем из (7.39) при

0=

′

υ

с учетом (7.37):

m

mM

Ll

12

−

=

. (7.43)

Как следует из (7.40), максимальное значение скорости цен-

тра стержня достигается при

l = 0. При этом условии шайба пере-

даст стержню максимальный импульс.

Значение

l, при котором скорость точки A сразу после удара

будет равна нулю, находим из (7.42) с учетом (7.37):

Ll

6

1

= . (7.44)

После попадания шайбы в точку с такими координатами

стержень сразу после удара будет совершать только вращательное

Глава 7. Законы сохранения момента импульса и механической энергии

245

движение вокруг мгновенной оси вращения, проходящей через

точку A.

Ответ:

1) шайба остановится сразу после удара, если

m

mM

Ll

12

−

=

;

2) шайба передаст стержню максимальный импульс, если она

попадет в центр масс стержня (

l = 0);

3) скорость точки A сразу после удара будет равна нулю при

условии

Ll

6

1

= .

Задача 7.3

Два одинаковых однородных вращающихся тела сфериче-

ской формы массой

m и радиусом r движутся навстречу друг другу

с одинаковыми по модулю скоростями

0

υ

. Угловые скорости вра-

щения тел,

1

ω и

2

ω , составляют угол

α

и равны по модулю

021

ω

== ωω . В результате лобового абсолютно неупругого соуда-

рения образуется одно тело той же плотности, форму которого

можно также считать сферической. Определить угловую скорость

ω вращения образовавшегося тела и изменение кинетической

энергии системы

k

Δ

E

.

Решение

I. Система двух тел в данной задаче предполагается изолиро-

ванной. Следовательно, суммарный импульс системы и суммарный

момент импульса в лабораторной инерциальной системе отсчета

сохраняются. Направим ось X лабораторной системы отсчета вдоль

линии, соединяющей центры масс двух тел до соударения.

II. Запишем закон сохранения проекции импульса рассматри-

ваемой системы тел на ось X для интервала

времени, включающего

момент их соударения:

υ

mmm 2

00

=− , (7.45)

где

υ

– проекция на ось X скорости поступательного движения

образовавшегося после соударения тела массой 2

m. Как видим,

0=

υ

, следовательно, движение образовавшегося тела является

чисто вращательным.

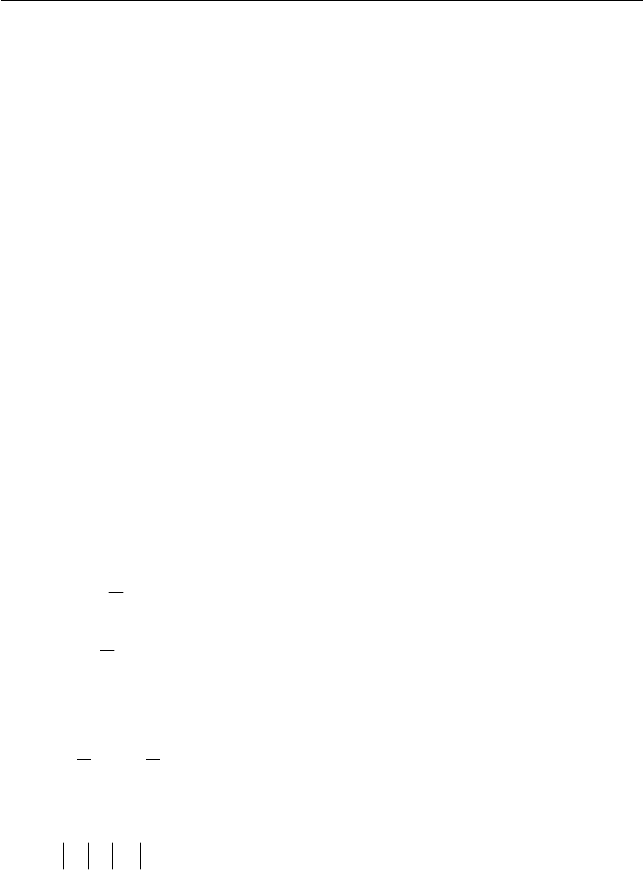
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

246

Запишем закон сохранения момента импульса рассматривае-

мой системы тел относительно их общего центра масс на интервале

времени, включающем момент их соударения:

LLL =

+

21

, (7.46)

где

1

L и

2

L – моменты импульса первого и второго тел до соуда-

рения,

L – момент импульса образовавшегося тела после соударе-

ния. Поскольку скорости тел до соударения направлены вдоль ли-

нии, на которой находится центр масс системы, то в соответствии с

формулой (6.27) Главы 6 момент импульса каждого из рассматри-

ваемых тел относительно центра масс системы тел равен моменту

импульса тела относительно его центра масс.

Моменты импульса

каждого из сферически симметричных

тел относительно их собственных центров масс в соответствии с

формулой (6.32) Главы 6 равны:

101

ωL J

=

, (7.47)

202

ωL J

=

, (7.48)

ωL J

=

, (7.49)

где

0

J и J – моменты инерции каждого из соударяющихся тел и

образовавшегося тела относительно их собственных осей враще-

ния. В соответствии с (6.45):

2

0

5

2

mrJ

= , (7.50)

2

)2(

5

2

RmJ = . (7.51)

Радиус

R образовавшегося тела находим из условия сохране-

ния плотности (а, следовательно, и объема):

33

3

4

3

4

2

Rr

ππ

= . (7.52)

Согласно условию задачи модули угловых скоростей враще-

ния тел до их соударения равны:

021

ω

== ωω . (7.53)

Изменение кинетической энергии рассматриваемой системы

тел

k

Δ

E

в результате их абсолютно неупругого соударения в соот-

ветствии с (7.6) равно:

Глава 7. Законы сохранения момента импульса и механической энергии

247

⎟

⎠

⎞

⎜

⎝

⎛

+−=

22

2

Δ

2

00

2

0

2

k

ωυω

JmJ

E . (7.54)

III. Решая систему уравнений (7.46) – (7.53), получаем мо-

дуль угловой скорости вращения образовавшегося в результате со-

ударения тела:

2

cos

2

cos2

3

0

α

ω

α

ωω

==

J

. (7.55)

Поскольку в соответствии с (7.46) – (7.49)

()

21

0

ωωω +=

J

,

(7.56)

а модули угловых скоростей вращения тел до их соударения равны

(7.53), то угловая скорость вращения образовавшегося тела

ω на-

правлена по биссектрисе угла

α

, образованного векторами угловых

скоростей

1

ω и

2

ω .

Искомое изменение кинетической энергии рассматриваемой

системы тел в результате соударения получим, подставляя (7.55) в

(7.54) с учетом (7.50) – (7.52):

()

=−

⎟

⎠

⎞

⎜

⎝

⎛

−+=

2

0

2

00

k

1cos1Δ

υαω

m

J

JE

()

2

0

3

2

0

2

1cos1

4

2

5

2

υαω

mmr −

⎟

⎠

⎞

⎜

⎝

⎛

−+=

. (7.57)

Задача 7.4

Две одинаковые гантели массой m в виде шариков, соеди-

ненных стержнем, скользят по гладкой

горизонтальной поверхности навстречу

друг другу со скоростями

1

υ

и

2

υ

так, как

изображено на рис. 7.7. Момент инерции

каждой гантели относительно оси, прохо-

дящей через ее центр масс перпендику-

лярно плоскости чертежа, равен J, а рас-

стояние между центрами шариков ганте-

ли – l. Как будут двигаться гантели после

абсолютно упругого соударения?

Рис. 7.7

A

B

D

1

υ

2

υ

C

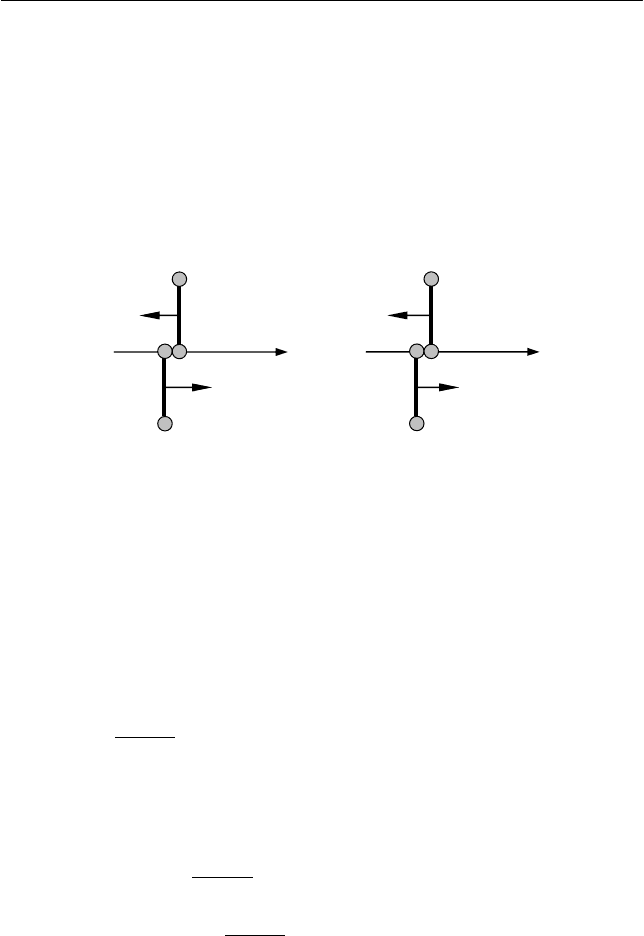
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

248

Решение

I. Задачу решаем в двух системах отсчета: лабораторной сис-

теме, ось X декартовой системы координат которой направим так,

как показано на рис. 7.8, и системе отсчета, связанной с центром

масс системы тел, с осью X', изображенной на рис. 7.9.

По условию задачи гантели движутся по гладкой горизон-

тальной поверхности, следовательно, центр масс системы тел, со-

стоящей из двух гантелей, движется с постоянной скоростью, и

система отсчета, связанная с центром масс, является инерциальной.

Поскольку рассматриваемая система тел замкнута, а соуда-

рение абсолютно упругое, то выполняются законы сохранения ме-

ханической энергии, импульса и момента импульса для этой систе-

мы в любой из выбранных систем отсчета.

II.

По условию задачи в лабораторной системе отсчета ганте-

ли движутся поступательно со скоростями

υ

1

и

υ

2,

следовательно,

проекция скорости центра масс на ось X лабораторной системы

отсчета (см. Главу 3) равна

2

21

цм

υυ

υ

−

= , (7.58)

а проекции скоростей центров масс гантелей

1

u и

2

u на ось X' от-

носительно системы центра масс обеих гантелей определяются вы-

ражениями:

uu =

+

=−=

2

21

цм11

υυ

, (7.59)

uu −=

+

−=−−=

2

21

цм22

υυ

. (7.60)

Рис. 7.8

A

B

D

υ

1

υ

2

C

X

Рис. 7.9

A

B

D

u

C

X'

Глава 7. Законы сохранения момента импульса и механической энергии

249

Запишем закон сохранения проекции импульса на ось X' для

системы двух гантелей на интервале времени, включающем момент

их соударения, в выбранной системе центра масс:

2121

umummumu

′

+

′

=+

, (7.61)

где

1

u

′

и

2

u

′

– скорости центров масс ган-

телей после соударения.

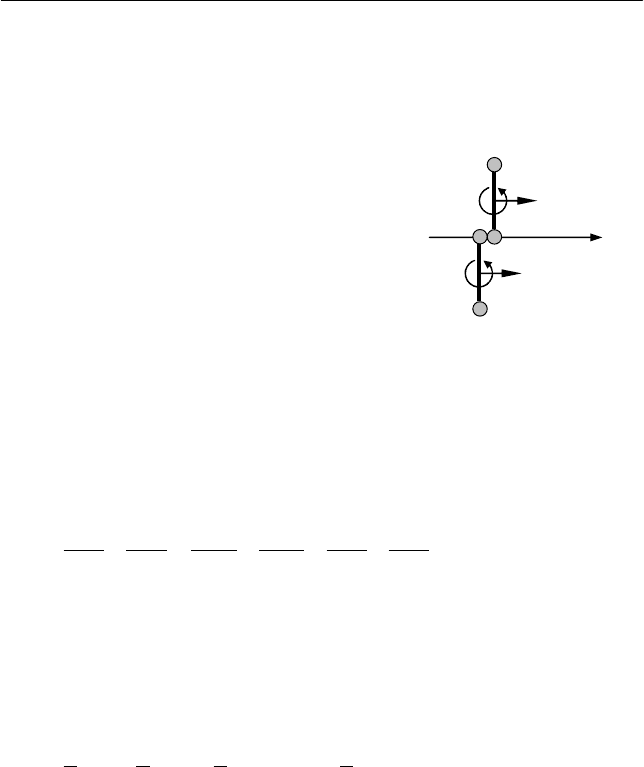
В общем случае после соударения

движение каждой гантели будет суперпо-

зицией поступательного движения ее цен-

тра масс и вращательного движения во-

круг оси, проходящей через ее центр масс

перпендикулярно поверхности, по кото-

рой происходит скольжение гантелей

(см. рис. 7.10).

Запишем закон сохранения механической

энергии системы

двух гантелей на интервале времени, включающем момент соуда-

рения, в системе их центра масс, при этом учтем, что при плоском

движении твердого тела его кинетическая энергия выражается фор-

мулой (7.10):

222222

2

1

2

1

2

1

2

1

ωω

JJumummumu

++

′

+

′

=+

. (7.62)

Здесь

1

ω

и

2

ω

– угловые скорости вращения гантелей после соуда-

рения.

Запишем также закон сохранения момента импульса системы

двух гантелей относительно оси, проходящей через их центр масс

перпендикулярно поверхности, по которой происходит скольжение

гантелей, на том же интервале времени:

221121

2222

ωω

Jum

l

Jum

l

mu

l

mu

l

+

′

−+

′

=+ . (7.63)

В (7.63) учтено, что момент импульса гантели относительно

выбранной оси в соответствии с формулой (6.23) из Главы 6 равен

сумме момента импульса центра масс гантели относительно этой

оси в системе центра масс двух гантелей и момента импульса ган-

тели относительно оси, проходящей через ее

центр масс, в системе

отсчета, связанной с этим центром масс.

Учитывая симметрию задачи в системе центра масс двух ган-

телей, запишем очевидные соотношения между угловыми скоро-

Рис. 7.10

B

A

D

ω

2

C

X'

2

u

′

ω

1

u

′

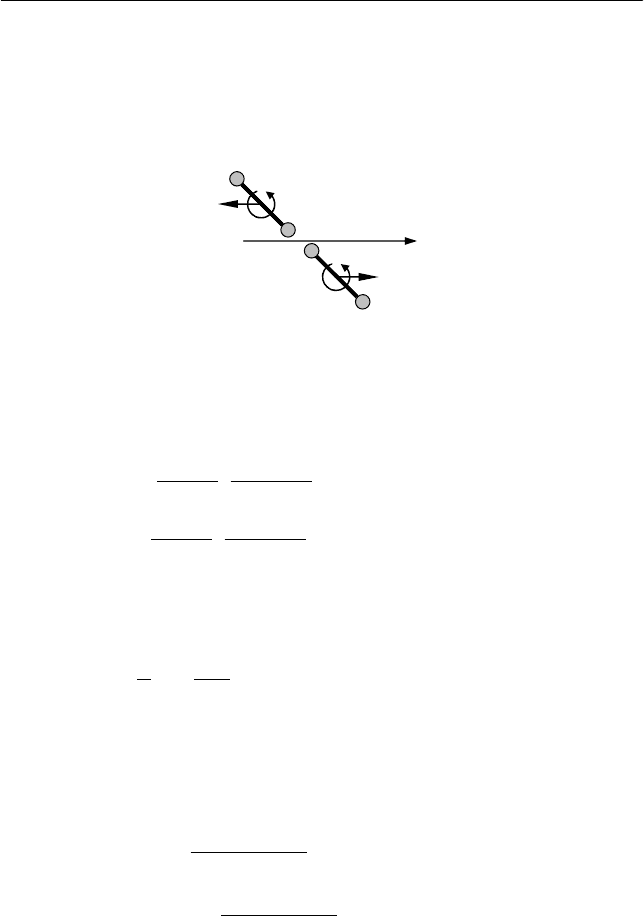
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

250

стями вращения гантелей и скоростями их центров масс после со-

ударения (см. рис. 7.11):

ω

=

21

, (7.64)

uuu

′

=

′

−

=

′

12

. (7.65)

III. Решим систему уравнений (7.59) – (7.65) относительно

1

u

′

,

2

u

′

,

1

ω

и

2

ω

:

u

J

m

l

Jml

uu

′

=

+

−

⋅

+

=

′

−=

′

4

2

21

υυ

, (7.66)

ω

υυ

ωω

=

+

⋅

+

==

J

m

l

lm

4

2

21

. (7.67)

Заметим, что момент инерции гантели при заданной массе m

максимален в случае, когда ее масса сосредоточена на концах ган-

тели:

42

2

mll

mJ =

⎟

⎠

⎞

⎜

⎝

⎛

≤ . (7.68)

Следовательно, в соответствии с (7.66) 0

21

≥

′

−

=

′

=

′

uuu (см.

рис. 7.11).

Скорости центров масс гантелей после соударения в лабора-

торной системе отсчета равны:

J

m

l

Jml

u

4

2

1

цм1

+

−

=+

′

=

′

υυ

, (7.69)

J

m

l

Jml

u

4

2

1

2

цм2

+

−

−=+

′

−=

′

υυ

. (7.70)

Итак, в результате абсолютно упругого соударения, движе-

ние гантелей представляет собой суперпозицию поступательного

Рис. 7.11

u

′

B

A

D

ω

C

X'

ω

u

′

Русаков В.С. и др. Механика. Методика решения задач

Подождите немного. Документ загружается.