Русаков В.С. и др. Механика. Методика решения задач

Глава 6. Кинематика и динамика абсолютно твердого тела

221

2

22

RmJ = . (6.138)

В соответствии с законом Амонтона–Кулона (см. п. 2.1.2 в

Главе 2) для сил трения покоя, действующих на цилиндры, спра-

ведливы неравенства:

1тр1

NF

μ

≤ . (6.139)

2тр2

NF

μ

≤ . (6.140)

III. Воспользовавшись соотношениями (6.130) − (6.138), вы-

разим силы нормальной реакции наклонной поверхности клина и

сил трения покоя со стороны этой поверхности на оба цилиндра

через величины, заданные в условии задачи, и искомый угол при

основании клина

α

:

α

cos

11

gmN

=

, (6.141)

α

cos

22

gmN

=

, (6.142)

α

sin

43

1

21

тр1

gm

mm

F

+

= , (6.143)

()

α

sin

43

2

21

тр2

gm

mm

F

+

= . (6.144)

Подставляя выражения (6.141) − (6.144) в неравенства (6.139)

и (6.140), получим условия, при которых качение цилиндров про-

исходит без проскальзывания:

21

43

mm

tg

+

≤

μα

, (6.145)

()

21

2

43

mm

tg

+

≤

μα

. (6.146)

Поскольку правая часть неравенства (6.146) меньше правой

части неравенства (6.145) при любых значениях коэффициента

трения

μ

и масс цилиндров m

1

и m

2

, то искомая область значений

угла при основании клина

α

, при которых цилиндры будут скаты-

ваться без проскальзывания, определяется неравенством (6.146).

В соответствии с (6.146) область возможных значений угла

α

однозначно определяется отношением масс цилиндров при задан-

ном значении коэффициента трения

μ

:

()

⎟

⎠

⎞

⎜

⎝

⎛

+

≤

1/2

4/3

arctg

21

mm

μα

. (6.147)

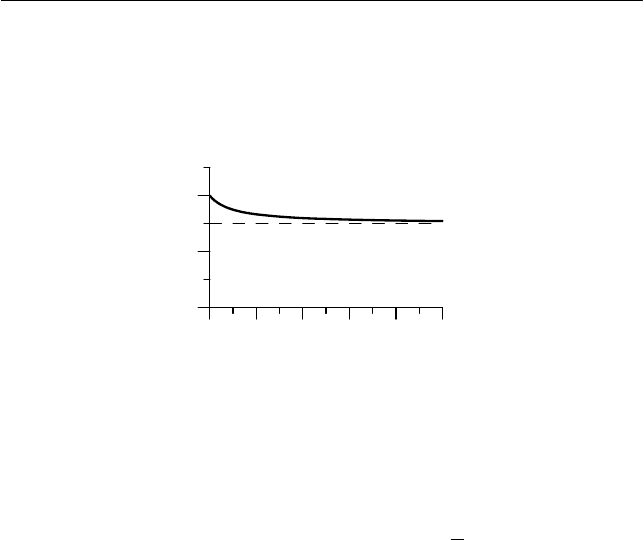
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

222

На рис. 6.18 изображен график зависимости предельной ве-

личины

μ

α

/tg

пр

от отношения массы сплошного цилиндра к мас-

се тонкостенного

21

/ mm .

Как видим, область значений угла

α

, при которых цилиндры

будут скатываться без проскальзывания, ограничена сверху пре-

дельным значением

пр

α

, которое равно

(

)

μ

2arctg

при

21

mm

<

и

асимптотически стремится к значению

⎟

⎠

⎞

⎜

⎝

⎛

μ

2

3

arctg

при неограни-

ченном увеличении отношения масс цилиндров

21

/ mm (рис. 6.18).

Задача 6.10

Цилиндрическая шайба радиусом

r = 3 см касается борта

гладкой горизонтальной площадки, имеющей форму круга радиу-

сом

R = 10 м. Шайбе придали скорость 30

0

=

υ

м/с, направленную

вдоль борта. Коэффициент трения между бортом и шайбой равен

1,0

=

μ

. Определить модуль скорости шайбы

к

υ

после того, как

прекратится проскальзывание между бортом и шайбой, а также ин-

тервал времени

t

к

, через который это произойдет.

Решение

I. Движение шайбы рассматриваем относительно лаборатор-

ной инерциальной системы отсчета, жестко связанной с горизон-

тальной площадкой. Уравнение движения центра масс шайбы бу-

дем записывать в проекциях на нормальную

n и тангенциальную

Рис. 6.18

21

/ mm

μ

α

/tg

пр

0246810

0

1

2

Глава 6. Кинематика и динамика абсолютно твердого тела

223

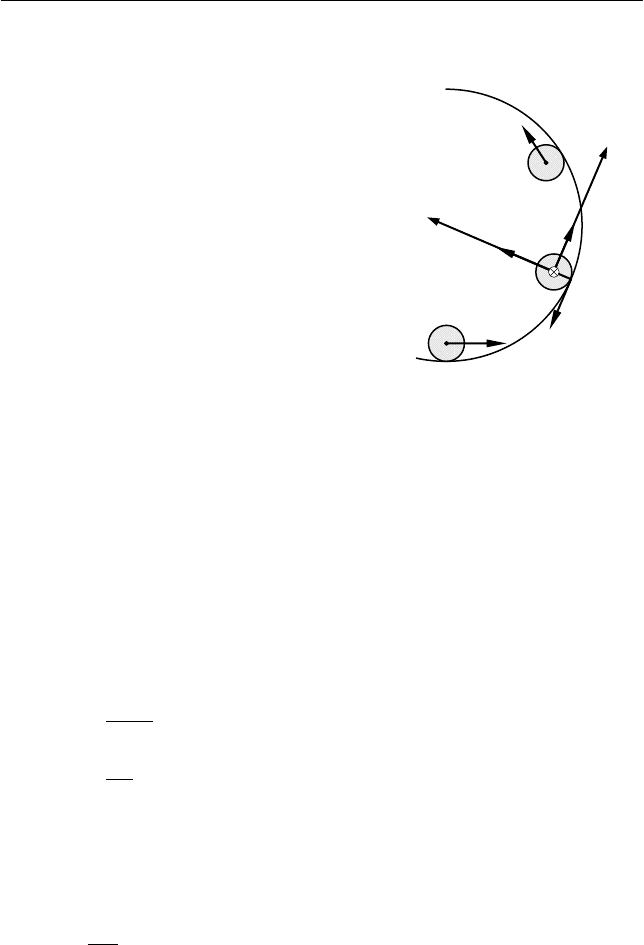
τ оси (см. п. 1.1. Теоретический материал в Главе 1), связанные с

центром движущейся шайбы (см. рис. 6.19).

При плоском движении шайбы

вдоль борта площадки на нее действуют

сила нормальной реакции

N

и сила тре-

ния

тр

F со стороны борта. При этом мо-

мент силы трения относительно оси, про-

ходящей через центр масс шайбы, вызы-

вает ее вращение вокруг указанной оси.

Скорость центра масс шайбы будет

уменьшаться, а угловая скорость ее вра-

щения

− увеличиваться, до тех пор, пока

не прекратится проскальзывание шайбы

о борт площадки. Начиная с этого мо-

мента сила трения шайбы о борт равна

нулю, а модуль скорости центра масс

шайбы не изменяется.

II. Запишем уравнение движения центра масс шайбы относи-

тельно лабораторной системы отсчета в проекциях на выбранные

нормальную

n и тангенциальную τ оси:

Nma

n

= , (6.148)

тр

Fma −=

τ

. (6.149)

Нормальная и тангенциальная проекции ускорения центра масс

шайбы определяются соотношениями (см. п. 1.1. Теоретический

материал в Главе 1):

rR

a

n

−

=

2

υ

, (6.150)

t

a

d

υ

τ

= , (6.151)

где

υ

− модуль скорости центра масс шайбы и )( rR

−

− радиус

кривизны его траектории.

Уравнение моментов (6.47) для вращающейся шайбы относи-

тельно оси, проходящей через ее центр масс, имеет вид:

rF

t

J

тр0

d

=

ω

. (6.152)

Момент инерции шайбы относительно указанной оси (6.44) равен:

Рис. 6.19

0

υ

)(t

υ

к

υ

n

τ

N

тр

F

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

224

2

0

mr

J =

. (6.153)

На начальном этапе (

к

tt

<

) шайба движется с проскальзыва-

нием и на нее в соответствии с законом Амонтона

− Кулона (см.

п. 2.1.2.В в Главе 2) действует сила трения скольжения, равная:

NF

μ

=

тр

. (6.154)

Запишем уравнение кинематической связи между угловой

скоростью вращения и скоростью центра масс шайбы после пре-

кращения проскальзывания (при

к

tt ≥ ):

ω

υ

r

=

. (6.155)

III. Воспользовавшись соотношениями (6.148)

− (6.151) и

(6.154), получим дифференциальное уравнение для модуля скоро-

сти центра масс шайбы на начальном этапе движения шайбы

(

к

tt < ):

rRt −

−=

2

d

υ

μ

υ

. (6.156)

Решаем уравнение (6.156) с помощью метода разделения пе-

ременных:

∫∫

−

−=

t

rR

0

2

d

0

μ

υ

, (6.157)

trR

rR

t

μυ

υυ

0

)(

+−

−

= . (6.158)

Связь угловой скорости вращения шайбы с модулем скоро-

сти ее центра масс получаем из (6.148) − (6.154):

()

2

d

υ

μω

rRrt −

= ,

(6.159)

Подставляя (6.158) в (6.159), получаем:

()

∫

+−

−

=

t

trR

r

rR

t

0

2

0

2

0

d

12

)(

μυ

ω

. (6.160)

В результате угловая скорость шайбы на начальном этапе ее

движения равна:

()

trRr

t

μυ

ω

0

2

0

2

)(

+−

= .

(6.161)

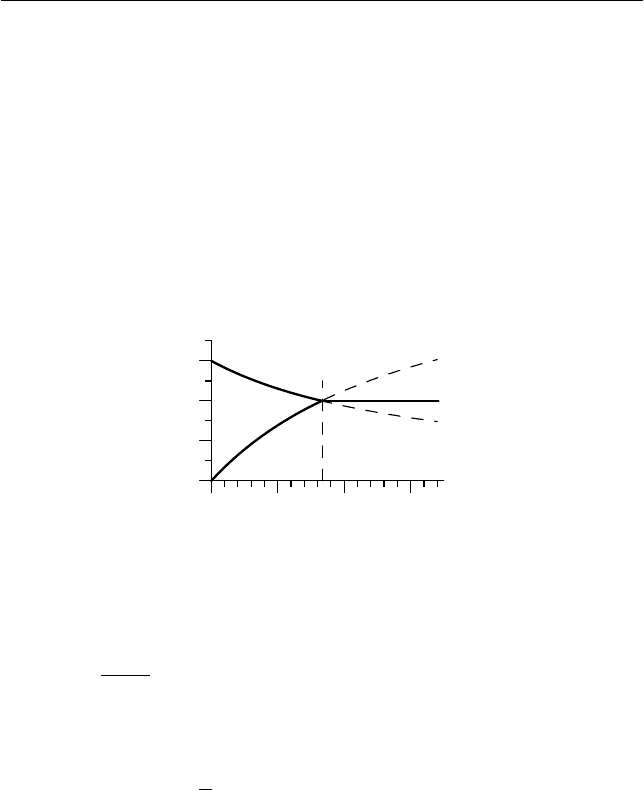
Глава 6. Кинематика и динамика абсолютно твердого тела

225

В соответствии с (6.158) модуль скорости центра масс шайбы

уменьшается от значения

0

υ

(при t = 0), в то время как угловая

скорость вращения шайбы увеличивается по закону (6.161). В мо-

мент прекращения проскальзывания (через интервал времени t

к

по-

сле сообщения шайбе скорости

0

υ

) угловая скорость вращения

шайбы и модуль скорости ее центра масс связаны уравнением ки-

нематической связи (6.157).

На рис. 6.20 представлены зависимости модуля скорости

центра масс шайбы

υ

и произведения угловой скорости вращения

шайбы на ее радиус

r

ω

.

Графики представленных зависимостей пересекаются в мо-

мент времени t

к

(см. рис. 6.20). Подставляя (6.158) (6.161) в уравне-

ние (6.157) получаем значение интервала времени t

к

:

0

к

2

μυ

rR

t

−

= . (6.162)

После прекращения проскальзывания при дальнейшем дви-

жении шайбы модуль скорости ее центра масс не меняется и равен:

0кк

3

2

)(

υυυ

==≡ tt . (6.163)

Как видим, искомый модуль скорости шайбы определяется

только ее начальной скоростью

0

υ

и не зависит от других величин,

заданных в условии задачи.

Подставляя заданные численные значения в (6.162) и (6.163),

находим искомые величины:

66,1

к

≅

t с, 20

к

=

υ

м/с.

Рис. 6.20

0123

0

10

20

30

t, c

,,

r

ω

υ

м/c

υ

r

ω

t

к

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

226

6.4. Задачи для самостоятельного решения

Задача 1

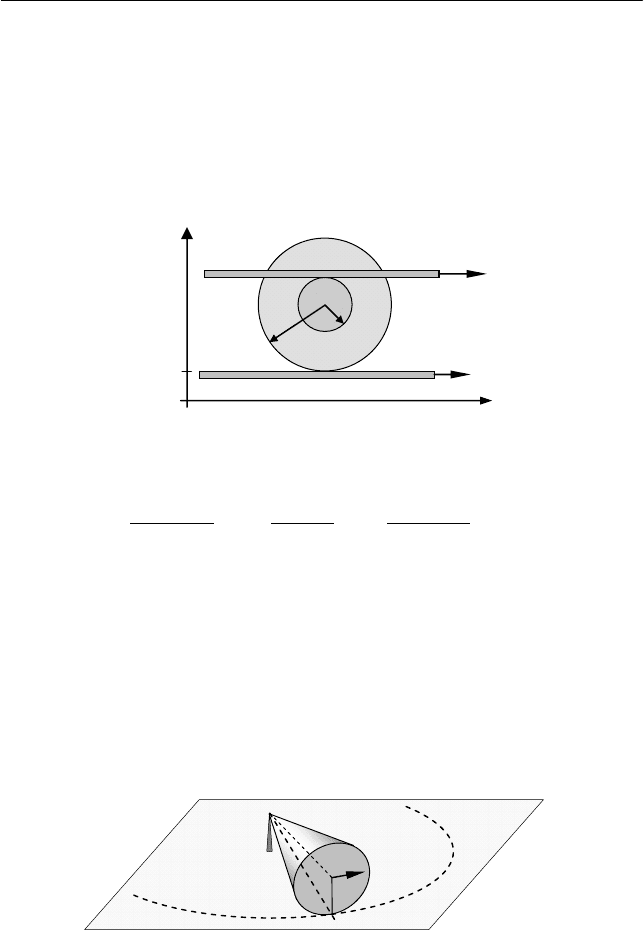
Две параллельные рейки движутся в одну сторону с постоян-

ными скоростями

υ

1

и

υ

2

относительно лабораторной системы от-

счета XY. Между рейками зажата катушка с радиусами R и r (см.

рис.), которая движется вдоль реек без проскальзывания.

Найти координату y

м

мгновенной оси вращения, угловую

скорость вращения

ω

катушки и скорость

υ

ее оси.

Ответ:

21

2

м

)(

υυ

υ

−

+

=

rR

y

,

)(

21

rR +

−

=

υυ

ω

,

rR

+

=

21

υυ

υ

.

Задача 2

Круглый конус высотой h и радиусом основания r катится

без скольжения по горизонтальной поверхности (см. рис.). Верши-

на конуса шарнирно закреплена в точке O на уровне центра осно-

вания конуса, который движется с постоянной по модулю скоро-

стью

υ

. Найти угловую скорость вращения конуса

ω

и его угловое

ускорение

β

.

0

X

Y

υ

1

υ

2

R

r

υ

r

h

O

Глава 6. Кинематика и динамика абсолютно твердого тела

227

Ответ:

2

1

⎟

⎠

⎞

⎜

⎝

⎛

+=

h

r

υ

ω

,

rh

2

υ

β

= .

Задача 3

Однородный диск радиусом R раскрутили вокруг его оси до

угловой скорости

ω

и положили на горизонтальную поверхность.

Коэффициент трения между поверхностью и диском равен

μ

. Че-

рез какое время

τ

угловая скорость вращения уменьшится в n = 2

раза.

Ответ:

g

R

μ

ω

τ

⋅=

8

3

.

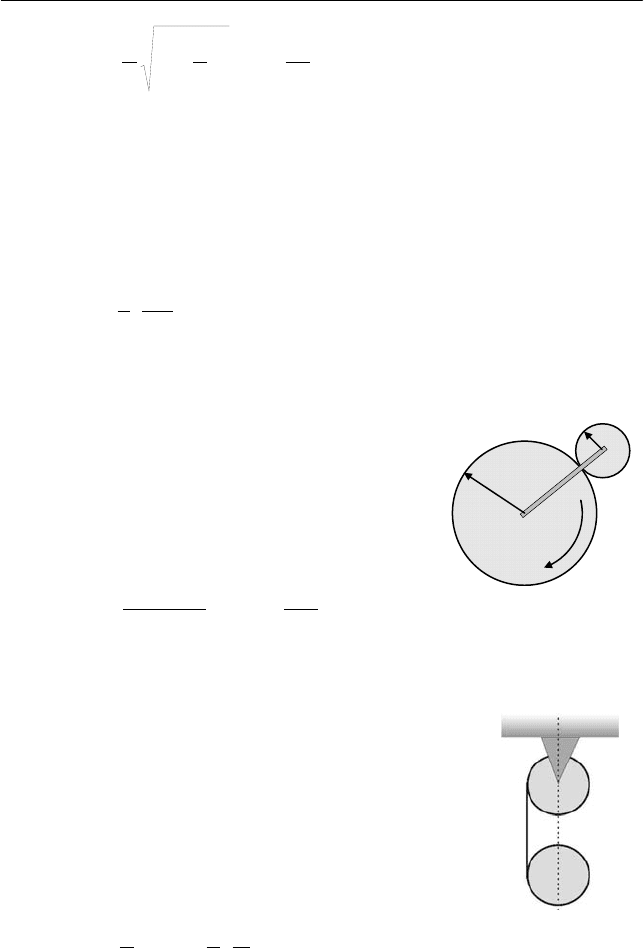
Задача 4

Кривошип, соединяющий оси двух

зубчатых колес радиусами R и r, вращается с

угловой скоростью

Ω

(см. рис.). Внутреннее

колесо неподвижно. Найти угловую скорость

вращения внешнего колеса

ω

и его относи-

тельную (по отношению к кривошипу) угло-

вую скорость вращения

отн

ω

.

Ответ:

r

rR )( +

=

Ω

ω

,

r

R

Ω

ω

=

отн

.

Задача 5

На два одинаковых однородных блока ра-

диусами R намотана легкая нерастяжимая нить

(см. рис.). В процессе движения оси блоков ос-

таются параллельными и находятся в вертикаль-

ной плоскости. Трением в закрепленной оси

верхнего блока, а также проскальзыванием нити

по блокам пренебречь. Найти модуль ускорения

оси нижнего блока a и модуль

его углового ус-

корения

β

.

Ответ:

ga

5

4

= ,

R

g

⋅=

5

2

β

.

R

r

Ω

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

228

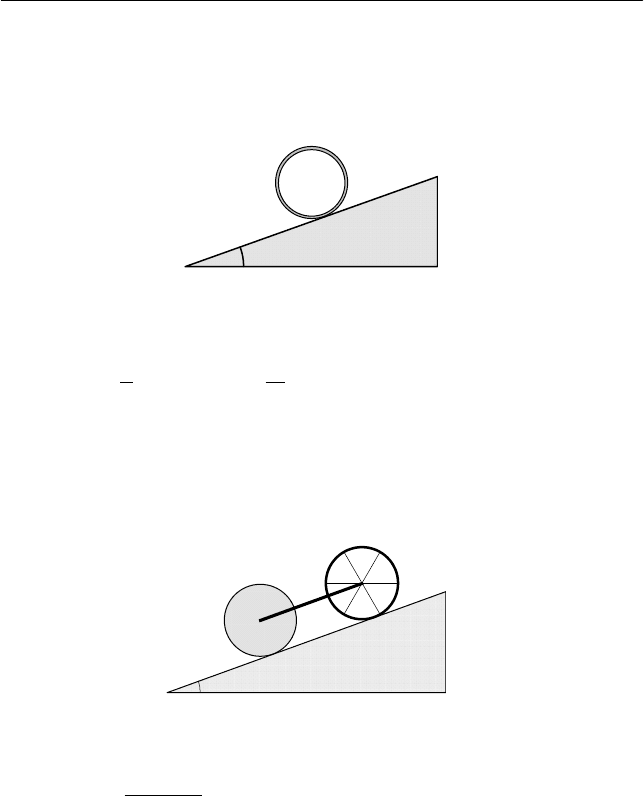
Задача 6

Тонкостенный цилиндр массой m скатывается без проскаль-

зывания по наклонной поверхности клина с углом при основании

α

(см. рис.).

Найти ускорение a оси цилиндра и силу трения, действую-

щая на него со стороны наклонной поверхности клина.

Ответ:

α

sin

2

1

ga = ,

α

sin

2

1

тр

mgF = .

Задача 7

Оси тонкостенного и сплошного цилиндров соединены неве-

сомым стержнем. Цилиндры скатываются без проскальзывания по

наклонной поверхности клина с углом при основании

α

(см. рис.).

Радиусы цилиндров одинаковы, масса каждого цилиндра m.

Определить силу F реакции стержня.

Ответ:

7

sin

α

mg

F =

.

Задача 8

Сплошному однородному цилиндру массой m и радиусом R

сообщили вращение вокруг его оси с угловой скоростью

ω

. Затем

положили его боковой поверхностью на горизонтальную плоскость

и предоставили самому себе. На какое расстояние переместится

цилиндр за время, в течение которого движение цилиндра проис-

α

Глава 6. Кинематика и динамика абсолютно твердого тела

229

ходило со скольжением. Коэффициент трения между поверхностью

и цилиндром равен

μ

.

Ответ:

g

R

x

μ

ω

18

Δ

22

= .

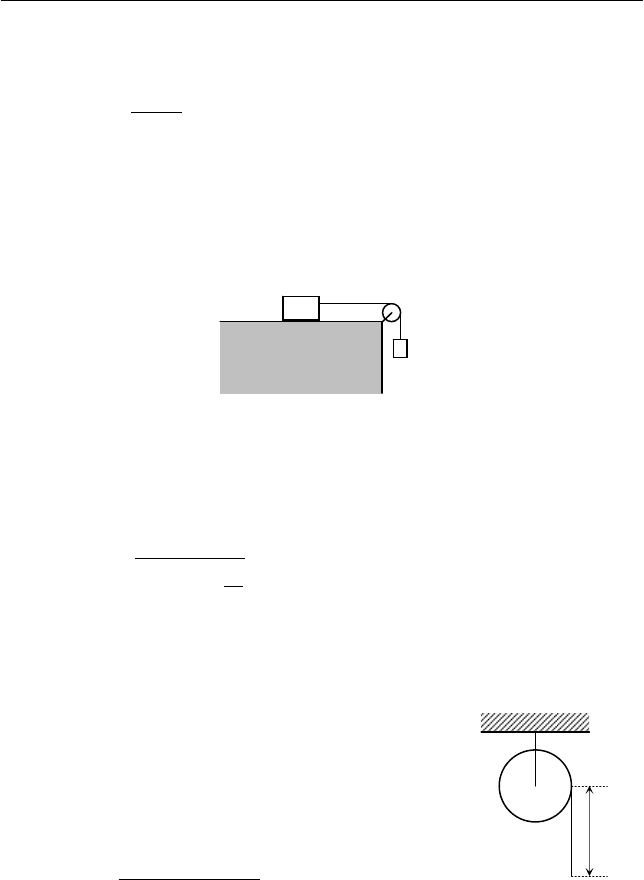
Задача 9

Два тела массами m

1

и m

2

соединены невесомой нерастяжи-

мой нитью, перекинутой через однородный блок массой m (см.

рис.).

Коэффициент трения между первым телом и горизонтальной

поверхностью равен

μ

. В процессе движения тел не происходит

проскальзывания нити по поверхности блока. Найти ускорение

второго тела, пренебрегая трением в оси блока.

Ответ:

2

21

12

m

mm

ga

++

−

=

μ

, при

12

mm

μ

> ;

0

=

a , при

12

mm

μ

≤

.

Задача 10

Однородный сплошной цилиндр массой M

может свободно вращаться вокруг своей непод-

вижной горизонтальной оси (см. рис.). На ци-

линдр намотана тонкая нить длиной L и массой

m. Найти ускорение a свешивающейся части

нити в зависимости от ее длины x.

Ответ:

)(2

2

xLmML

mgx

a

−+

= .

m

1

m

2

x

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

230

Задача 11

Система тел, состоящая из груза и двух

одинаковых блоков, изображена на рисунке.

Ось левого блока закреплена, а правый блок

свободно лежит на нити. При движении тел

системы не происходит проскальзывания ни-

ти относительно поверхностей блоков. Счи-

тая заданными массу груза m, массы блоков

M и их радиусы R, определить ускорение гру

-

за

a. Трением в оси блока пренебречь.

Ответ:

g

Mm

a

2

7

+

=

.

m

M

Русаков В.С. и др. Механика. Методика решения задач

Подождите немного. Документ загружается.