Руев Г.А. и др. Методы вычислений и их реализация в Excel
Подождите немного. Документ загружается.


81
Модифицированный метод Эйлера
В данном методе вычисление
1+i
y
состоит из двух этапов:
(
)
iiii
yxhfyy ,
~
1
+
=
+
,
( ) ( )
[ ]
111
~
,,
2
+++
++=
iiiiii
yxfyxf
h
yy
. (5.7)
Данная схема называется также методом предиктор-корректор.
Это английское название, означающее «предсказать-исправить».
Действительно, на первом этапе приближенное значение
предсказывается с первым порядком точности, а на втором этапе это
предсказание исправляется, так что результирующее значение имеет
второй порядок точности.
Методы Рунге-Кутты
Идея построения явных методов Рунге-Кутты
p
-го порядка
заключается в получении приближений к значениям
(
)
1+i
xy
по
формуле вида
(
)
hyxhyy
iiii
,,
1
ϕ
+
=
+
, где
( ) ( )
∑
=
=
q
n
i
nnii
hkchyx
1
,,
ϕ
(
)
(
)
ii
i
yxfhk ,
1
=
,
(
)
(
)
(
)
hkyhxfhk
i
ii
i
12122
,
βα
++=
,
(
)
(
)
(
)
(
)
hkhkyhxfhk
ii
ii
i
23213133
,
ββα
+++=
,
…
(
)
(
)
(
)
(
)
hkhkyhxfhk
i
qqq
i
qiqi
i
q 11,11
...,
−−
++++=
ββα
.
Здесь
, , 0
n nj
j n q
α β
< < ≤
– некоторые фиксированные числа
(параметры), которые подбирают таким образом, чтобы получить
нужный порядок аппроксимации p.
Как правило, для каждого p существует не одна схема Рунге-
Кутты порядка p, а целое параметрическое семейство. Так, схемы
Рунге-Кутта второго порядка точности образуют
однопараметрическое семейство
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

82
( )
( )
[ ]
.1
2
,
2
,,
21
2
1
11
ii
ii
i
ii
i
ii
i
akkahyy
k
a
h
y
a
h
xfkyxfk
+−+=
++==
+
(5.8)
Выделим из семейства методов (5.8) два наиболее простых и часто
используемых частных случая.
При
2
1
=a
получаем формулы
(
)
(
)
[ ]
..210,
2
,,,
21
12
1
1
,.,,ikk
h
yy
hkyhxfkyxfk
ii
ii
i
ii
i
ii
i
=++=
++==
+
, (5.9)
которые совпадают с формулами модифицированного метода Эйлера
(5.7).
При a=1 выводим новый простой метод
( )
..210,
2
,
2
,,
21
12
1
,.,,ihkyy
k
h
y
h
xfkyxfk
i
ii
i
ii
i
ii
i
=+=
++==
+
,
который называется методом средней точки.
Схема Рунге-Кутта четвертого порядка точности.
При p=4 можно получить один из вариантов метода:
( )
( )
( )
,...2,1,0,22
6
,,,
2
,
2
,
2
,
2
,,
43211
34
2
3
1
21
=++++=
++=
++=
++==
+
ikkkk
h
yy
hkyhxfk
hk
y
h
xfk
hk
y
h
xfkyxfk
ii
iiii
iiii
(5.10)
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

83
ПРИМЕР 5.1.
Решить задачу Коши:
(
)
( )
10,2
2
=+= yyx
dx
dy
на отрезке
[
]
1,0
с шагом
1
,
0
=
h
с
помощью явного метода Эйлера (5.5), модифицированного метода
Эйлера (5.7) и четырехэтапного метода Рунге-Кутта (5.10).
Точное решение:
(
)
5,05,1
22
−−−= xxexy
x
.
Построим разностную сетку
9,...,1,0, =⋅= ihix
i
.
Расчетные формулы по явному методу Эйлера для данного примера:
1
0
=
y
,
(
)
9,...,1,0,2
2
1
=+⋅⋅+=
+
iyxhyy
iiii
.
Расчетные формулы модифицированного метода Эйлера:
1
0
=
y
,
(
)
iiii
yxhyy +⋅⋅+=
+
2
1
2
~
,
( ) ( )
[ ]
1
22
1
~
22
2
++
+⋅++⋅+=
iiiiii
yxyx
h
yy
,
Расчетные формулы метода Рунге-Кутта:
1
0
=
y
,
( )
( )
( )
.9,...,2,1,0,22
6
,
2
2,
22
2
,
22
2,2
43211
3
2
4
2
2
3
1
2
2
2
1
=++++=
+++⋅=
++
+⋅=
++
+⋅=+⋅=
+
ikkkk
h
yy
hk
yhxk
hk
y
h
xk
hk
y
h
xkyxk
ii
iiii
iiii
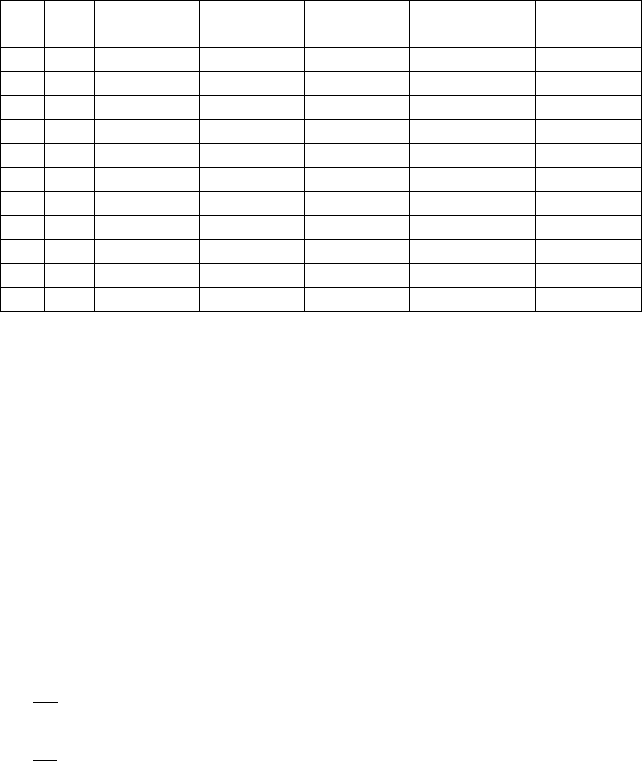
Результаты вычислений в Excel приведены ниже
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
84
i
i
x
Эйлер
i
y
~
Модиф.
Эйлер
Рунге-
Кутта
Точное
0 0
1
1
1
1
1
1 0.1
1.2
1.2
1.22
1.218393
1.222104
2 0.2
1.442
1.462
1.488593
1.488609
1.497737
3 0.3
1.7384
1.788993
1.824368
1.826287
1.843178
4 0.4
2.10408
2.200166
2.24674
2.250465
2.278311
5 0.5
2.556896
2.718774
2.779016
2.784329
2.827423
6 0.6
3.118275
3.372771
3.449508
3.456112
3.520175
7 0.7
3.81393
4.196062
4.292669
4.300192
4.3928
8 0.8
4.674716
5.229881
5.350447
5.358432
5.489549
9 0.9
5.73766
6.524423
6.673919
6.68181
6.864471
10
1
7.047191
8.140804
8.325282
8.332399
8.583584
Видно, что в сравнении с точным решением, самым точным является
метод Рунге – Кутта.
Численные методы решения систем ОДУ первого
порядка
Рассмотренные выше методы решения задачи Коши для одного
уравнения могут быть использованы также для решения систем
дифференциальных уравнений первого порядка и уравнений высших
порядков.
Пусть задана задача коши для системы двух уравнений первого
порядка:
( )
zyx
dx
dy
,,
ϕ
=
( )
zyx
dx
dz
,,
ψ
=
(
)
(
)
0000
, zxzyxy
=
=
Обобщим формулы явного метода Эйлера (5.5):
(
)
iiiii
zyxhyy ,,
1
ϕ
+
=
+
(
)
iiiii
zyxhzz ,,
1
ψ
+
=
+
,
модифицированного метода Эйлера (5.7):
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

85
(
)
( )
iiiii
iiiii
zyxhzz
zyxhyy
,,
~
,,
~
1
1
ψ
ϕ
+=
+
=
+
+
( ) ( )
[ ]
( ) ( )
[ ]
iiiiiiii
iiiiiiii
zyxzyx
h
zz
zyxzyx
h
yy
~
,
~
,,,
2
~
,
~
,,,
2
1
1
ψψ
ϕϕ
++=
++=
+
+
,
схемы Рунге-Кутта четвертого порядка точности (5.10):
( )
( )
( ) ( )
( ) ( )
,,,,,,
,
2
,
2
,
2
,
2
,
2
,
2
,
2
,
2
,
2
,
2
,
2
,
2
,,,,,,
22
6
22
6
334334
22
3
22
3
11
2
11
2
21
43211
43211
hlzhkyhxlhlzhkyhxk
hl
z
hk
y
h
xl
hl
z
hk
y
h
xk
hl
z
hk
y
h
xl
hl
z
hk
y
h
xk
zyxlzyxk
llll
h
zz
kkkk
h
yy
iiiiii
iiiiii
iiiiii
iiiiii
ii
ii
+++=+++=
+++=
+++=
+++=
+++=
==
++++=
++++=
+
+
ψϕ
ψϕ
ψϕ
ψϕ
Вычисления приближенного решения проводятся путем
последовательного применения этих формул.
Рассмотрим задачу Коши для уравнения второго порядка
( ) ( )
0000
2
2
,,,, zx
dx
dy
yxy
dx
dy
yxf
dx
yd
==
=
Введем вторую неизвестную функцию
( )
dx
dy
xz =
. Тогда исходная
задача Коши для уравнения сводится к следующей задаче для системы
двух ОДУ первого порядка:
( ) ( ) ( )
0000
,,,, zxzyxyzyxf
dx
dz
z
dx
dy
===
=
,
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

86
которая решается с помощью методов, описанных выше.
ПРИМЕР 5.2.
Найти решение задачи Коши:
( ) ( ) ( )
00,10,2
2
2
===++
dx
dy
yxxy
dx
dy
dx
yd
на отрезке
[
]
1,0
.
Точное решение:
(
)
223 −++=
−−
xxeexy
xx
.
Проверим, что точное решение удовлетворяет данному
дифференциальному уравнению. Действительно:
( )
( )
( ) ( )
010,120030
2231222
2
2
12
00
2
2
2
2
=+−==−++=
=−++++−−++−=
=++
+−=
+−−=
−−−−−−
−−
−−
e
dx
dy
ey
xxxeexeexee
xy
dx
dy
dx
yd
xee
dx
yd
xee
dx
dy
xxxxxx
xx
xx
Решим задачу явным методом Эйлера (5.5), модифицированным
методом Эйлера (5.7) и методом Рунге-Кутты (5.10) на сетке с шагом
2
,
0
=
h
.
Введем функцию
( )
dx
dy
xz =
и получим следующую задачу Коши
для системы двух ОДУ первого порядка:
( ) ( )
00,10,2 ==+−−=
=
zyxyz
dx
dz
z
dx
dy
.
Используем формулы явного метода Эйлера:
iii
hzyy
+
=
+1
(
)
iiiii
xyzhzz
+
−
−
+
=
+
2
1
0,1
00
=
=
zy
,
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
87
модифицированного метода Эйлера:
( )
iiiii
iii
xyzhzz
hzyy
+−−+=
+
=
+
+
2
~
~
1
1
[ ]
( ) ( )
[ ]
hxx
xyzxyz
h
zz
zz
h
yy
ii
iiiiiiii
iiii
+=
+−−++−−+=
++=
+
++
+
1
11
1
~
~
22
2
~
2
.
четырехэтапного метода Рунге – Кутты:
( )
( )
( ) ( )
.2,
,
222
2,
2
,
222
2,
2
,2,
22
6
22
6
33434
22
3
2
3
11
2
1
2
11
43211
43211
hxhkyhlzlhlzk
h
x
hk
y
hl
zl
hl
zk
h
x
hk
y
hl
zl
hl
zk
xyzlzk
llll
h
zz
kkkk
h
yy
iiii
iiii
iiii
iiii
ii
ii
+++−+−=+=
++
+−
+−=+=
++
+−
+−=+=
+−−==
++++=
++++=
+
+
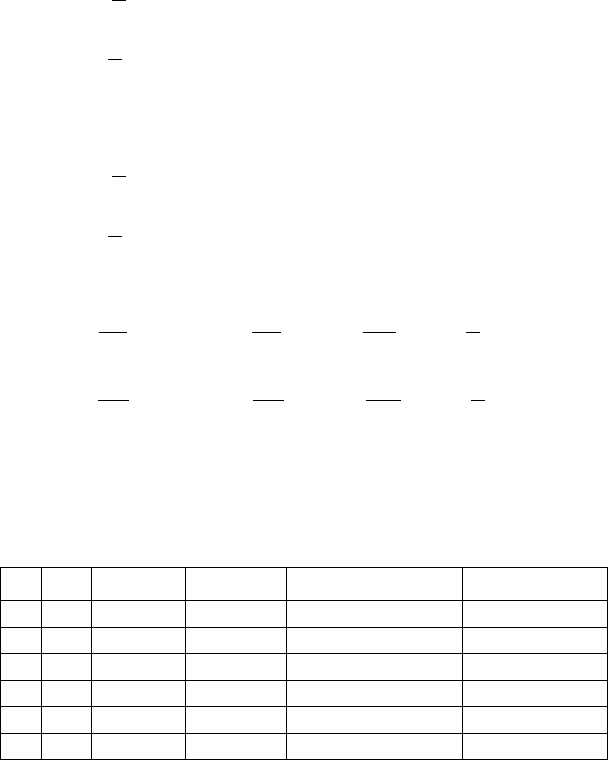
Решение оформим в виде таблиц.
Схема Эйлера:
k
i
x
i
y
i
z
Точное решение
Погрешность
0
0
1
0
1
0
1
0.2
1
-0.2
0.983685
0.016315
2
0.4
0.96
-0.28
0.947216
0.012784
3
0.6
0.904
-0.28
0.905009
0.001009
4
0.8
0.848
-0.2288
0.866913
0.018913
5
1
0.80224
-0.14688
0.839397
0.037157
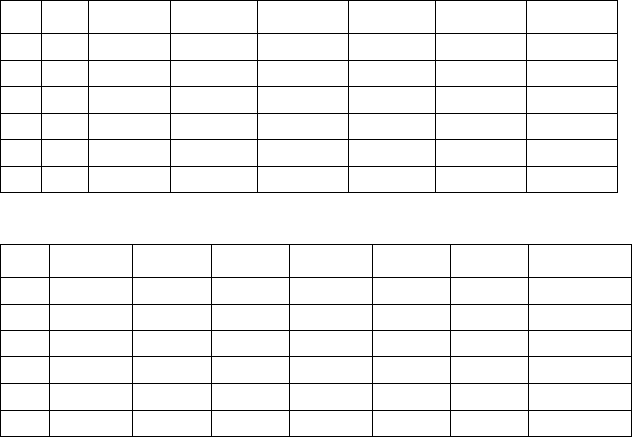
Модифицированный метод Эйлера:
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
88
k
i
x
i
y
~
i
z
~
i
y
i
z
Точ.реш Погреш.
0 0 1 0 1 0 1 0
1 0.2 1 -0.2 1 -0.18 0.983685 0.016315
2 0.4 0.964 -0.268 0.962 -0.244 0.947216 0.014784
3 0.6 0.9132 -0.2588 0.9108 -0.2342 0.905009 0.005791
4 0.8 0.86396
-0.20268 0.8615 -0.178 0.866913 0.005413
5 1 0.8259 -0.1191 0.823432 -0.09441 0.839397 0.015965
Схема Рунге-Кутта:
i
x
i
y
i
z
1
k
1
l
4
k
4
l
Погреш.
0
1
0
0
0.2
0.9837
-0.146
0
-1
-0.15
-0.486
1.79E-05
0.4
0.9472
-0.207
-0.146
-0.491
-0.209
-0.13
2.76E-05
0.6
0.905
-0.207
-0.207
-0.134
-0.209
0.113
3.18E-05
0.8
0.8669
-0.168
-0.207
0.1097
-0.17
0.272
3.25E-05
1
0.8394
-0.104
-0.168
0.2695
-0.105
0.37
3.09E-05
Как можно видеть, максимальная погрешность, определяемая как
разность между точным и рассчитанным значением функции
y
, в
методе Рунге-Кутта не превышает
5
1025,3
−
⋅
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

89
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ РЕШЕНИЯ КРАЕВЫХ
ЗАДАЧ ДЛЯ ОДУ
Постановка задачи
Найти решение линейного дифференциального уравнения
(
)
(
)
(
)
xzuxeuxqu
=
−
′
+
′
′
,
[
]
bax ,
∈
, (6.1)
удовлетворяющего краевым условиям:
(
)
(
)
ψ
ϕ
=
=
buau ,
(6.2)
К такому виду задач сводится, например, задача об определении
прогибов балки, которая на концах опирается шарнирно.
Теорема.
Пусть
(
)
(
)
[
]
(
)
(
)
0;,,,
2
≥
∈
xebaCxzxexq
.
Тогда существует единственное решение поставленной задачи.
Решение будем отыскивать методом конечных разностей.
Основные этапы метода конечных разностей:
1. Область непрерывного изменения аргумента
[
]
ba,
заменяется
дискретным множеством точек, называемых узлами:
h
b
nniihax
i
1
,,...,1,0,
−
==+=
.
2. Искомая функция непрерывного аргумента
x
приближенно
заменяется функцией дискретного аргумента на заданной сетке, т.е.
(
)
(
)
nh
uuuxu ,...,
0
=
→
. Функция
h
u
называется сеточной.
3. Исходное дифференциальное уравнение заменяется
алгебраическим разностным уравнением относительно сеточной
функции. Такая замена называется разностной аппроксимацией.
Таким образом, решение дифференциального уравнения сводится к
отысканию значений сеточной функции в узлах сетки, которые
находятся из решения алгебраических уравнений.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

90
Аппроксимация производных
Для аппроксимации первой производной можно воспользоваться
формулами:
( )
( )
h
uu
Lxu
ii
hi
−
=≈
′
++ 1
– правая разностная производная,
( )
( )
h
uu
Lxu
ii
hi
1−−
−
=≈
′
– левая разностная производная,
( )
( )
(
)
(
)
h
uuLL
Lxu
iihh
hi
2
2
110 −+
−+
−
=
+
=≈
′
– центральная разностная
производная.
Существует множество способов аппроксимации производной,
которые следуют из определения производной:
( )
(
)
(
)
x
xuxxu
xu
x
∆
−
∆
+
=
′
→∆ 0
lim
.
На основе формул для разностной аппроксимации первой
производной можно построить разностную аппроксимацию второй
производной:
( ) ( )( )
( ) ( )
( )
ih
iii
iiii
ii
ii
uL
h
uuu
h
h
uu
h
uu
h
xuxu
xuxu
2
2
11
11
1
2
=
+−
=
=
−
−
−
=
′
−
′
≈
′
′
=
′′
−+
−+
+
(6.3)
Аналогично можно получить аппроксимации производных более
высокого порядка.
Определение.
Погрешностью аппроксимации
n
-ой производной называется
разность
(
)
(
)
(
)
(
)
(
)
xuLxux
n
h
n
−=
δ
.
Для определения порядка аппроксимации используется
разложение в ряд Тейлора.
Рассмотрим правую разностную аппроксимацию первой
производной:
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
