Руев Г.А. и др. Методы вычислений и их реализация в Excel
Подождите немного. Документ загружается.

71
Для оценки погрешности метода
( ) ( )
( ) ( )
∫∫
∑∑
∫
∑
∫
−−
−
−=
−=
=
−=
−=Ψ
−−
==
−
=
−
i
i
i
i
i
i
x
x
ii
x
x
i
n
i
i
n
i
i
x
x
n
i
i
b
a
n
dxxfxfhxfdxxf
xhfdxxfxfhdxxf
11
1
2
1
2
1
11
2
1
1
2
1
ϕ
ϕ
.
воспользуемся формулой Тейлора:
( ) ( ) ( )
[ ]
iii
i
i
i
i
i
xxxxfxxfxfxf ,,
2
1
1
2
2
1
2
1
2
1 −
−−−
∈
−
′′
+
−
′
+
=
ξξξ
.
Тогда
( ) ( )
( ) ( )
( )
( )
( )
( )
−−
−
′′
+
−−
−
′
=
=
−
′′
+
−
′
=
=
−
′′
+
−
′
=
=
−
−
′′
+
−
′
+
=
−
−
−−
−
−
−−
−−
−−−−
−−
−
−
∫
∫
3
2
11
3
2
1
2
2
11
2
2
1
3
2
1
2
2
1
2
2
1
2
1
2
1
2
2
1
2
1
2
1
6
1
2
6
1
2
2
1
2
1
11
1
1
i
i
i
ii
i
i
i
i
i
x
x
i
i
x
x
i
i
x
x
i
i
i
i
x
x
ii
i
i
i
i
i
xxxxfxxxx
f
xxfxx
f
dxxxfxxf
dxxfxxfxxfxf
i
i
i
i
i
i
i
i
ξ
ξ
ξ
ξ
ξξ
ξξϕ
Поскольку
2
2
1
h
xx
i
i
=−
−
и
2
2
11
h
xx
i
i
−=−
−
−
, то
( ) ( )
iii
f
hhh
f
ξξϕ
′′
=
+
′′
=
24886
1
3
33
Пусть
[ ]
(
)
xfM
bax
′′
=
∈ ,
max , тогда
( ) ( )
ab
Mh
Mn
h
M
h
f
h
n
i
n
i
in
−==≤
′′
=Ψ
∑∑
==
2424
1
2424
23
1
3
1
3
ξ
,
т.е. формула средних прямоугольников имеет второй порядок
точности.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
72
Формула трапеций
Во всех рассмотренных формулах площадь криволинейной
трапеции заменялась на площадь прямоугольников.
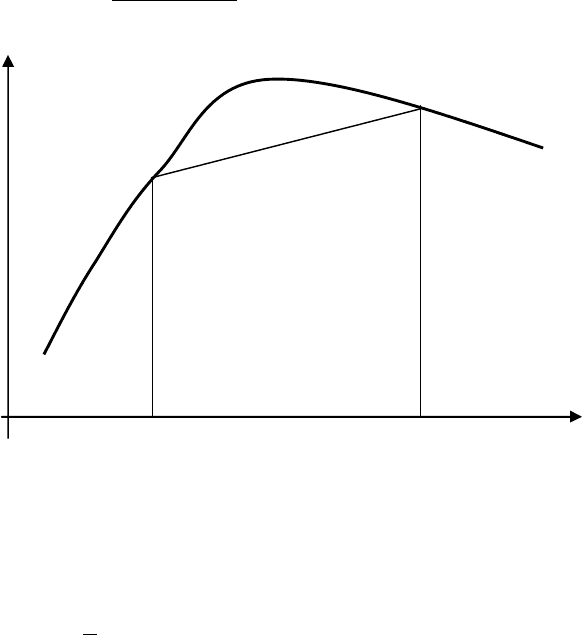
В методе трапеций криволинейная трапеция заменяется на
прямоугольную (рис. 4.3), площадь которой вычисляется по
известным формулам:
( )
(
)
(
)
( )
1
1
2
1
−
−
−
+
≈
∫
−
ii
ii
x
x
xx
xfxf
dxxf
i
i
.
Рис. 4.3. Метод трапеций
Формула трапеций может быть также получена путем замены
подынтегральной функции интерполяционным полиномом первой
степени:
( ) ( ) ( ) ( ) ( )
[ ]
11,1
1
−−
−−−=
iiiii
xfxxxfxx
h
xL
.
x
(
)
xf
1−i
x
i
x
y
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

73
Действительно
( ) ( ) ( ) ( ) ( )
( ) ( )
( )
( ) ( )
h
xfxf
hxf
h
hxf
h
dxxfxx
h
dxxfxx
h
dxxL
ii
ii
x
x
ii
x
x
ii
x
x
i
i
i
i
i
i
i
22
1
2
1
11
1
2
1
2
11,1
111
−
−
−−
+
=−−=
=−−−=
∫∫∫
−−−
.
Тогда для всего отрезка
[
]
ba,
получим:
( ) ( )
(
)
(
)
∑∑
∫∫
=
−
=
+
==
−
n
i
ii
n
i
x
x
b
a
h
xfxf
dxxfdxxf
i
i
1
1
1
2
1
.
Можно показать, что формула трапеций совпадает с формулой
средних для таблично заданной функции и также имеет второй
порядок точности.
Формулу трапеций можно также записать в виде:
( )
(
)
(
)
( )
+
+
=
∑
∫
=
n
i
i
b
a
xf
bfaf
hdxxf
1
2
.
Формула Симпсона
При вычислении интеграла
( )
∫
−
i
i
x
x
dxxf
1
с помощью метода Симпсона (парабол),
функцию
(
)
xf
на локальном отрезке
[
]
ii
xx ,
1−
заменяют
параболой, проходящей через точки
(
)
(
)
11
,
−− ii
xfx
,
−−
2
1
2
1
,
ii
xfx
,
(
)
(
)
ii
xfx ,
,
где
2
1
2
1
ii
i
xx
x
+
=
−
−
– середина локального отрезка.
Построим полином Лагранжа второй степени:
(
)
(
)
[
]
iii
xxxxLxf ,,
1,2 −
∈
≈
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
74
( )
( ) ( )( )
( )
−−+
−−−−
−
=
−
−
−−
−
i
i
i
i
iiii
i
i
fxxxx
fxxxxfxxxx
h
xL
2
1
2
111
2
1
2
,2
2
2
.
Здесь
(
)
ii
xff
=
,
=
−−
2
1
2
1
ii
xff
,
(
)
11 −−
=
ii
xff
.
Тогда
( ) ( )
( )
( )( )
( )
( )
( )( )
( )
++=
=
−+
−−
−=
=
−−−+
−−−
−−
+−
=
=
−−+
−−
−−
−
==
−
−
−
−
−
−−
−
−
−
−
−
−
−
∫
∫
∫
∫
∫
∫
∫∫
−
−
−
−
−
−
−−
i
i
i
i
i
i
x
x
iii
x
x
ii
i
x
x
iii
x
x
i
ii
x
x
ii
i
x
x
i
i
i
x
x
i
x
x
fff
h
hh
f
hh
f
hh
f
h
dx
h
xxxxf
dxhxxxxf
dxxx
h
xxf
h
dxxxxxf
dxxxxxf
dxxxxxf
h
dxxLdxxf
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
2
11
3333
2
1
33
1
2
1
11
2
1
1
2
2
1
1
2
1
2
11
2
,2
4
6
4323
2
43
2
2
2
2
2
2
2
1
1
1
1
1
1
11
Таким образом, мы получаем формулу Симпсона
( ) ( ) ( )
∑
∫
=
−
−
+
+
+==
n
i
i
ii
i
b
a
xf
xx
fxf
h
dxxf
1
1
1
2
4
6
.
Можно показать, что формула Симпсона имеет четвертый
порядок точности.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
75
ПРИМЕР 4.1.
Вычислить интеграл J=
( )
( )
∫
−
−−
2
1
2
13 dxxx
.
Найдем значение определенного интеграла точно:
=+=
b
a
x
xxx
3
2
3-
4
-
4
J
234
5,25.
Разобьем отрезок
[
]
2,1
−
на 10 частей, т.е.
(
)
3,0
10
12
=
−
−
=h
.
Вычислим значение интеграла по формулам левых, правых, средних
прямоугольников, по формуле трапеций и формуле Симпсона.
Для этого составим таблицы:
i
i
x
(
)
i
xf
2
1+
+
ii
xx
+
+
2
1ii
xx
f
i
i
i
fff
+
+
−
−
2
11
4
0 -1
4
-0.85
4.213375
25.1205
1 -0.7
4.267
-0.55
4.181125
24.9675
2 -0.4
3.976
-0.25
3.671875
21.9525
3 -0.1
3.289
0.05
2.847625
17.0475
4 0.2
2.368
0.35
1.870375
11.2245
5 0.5
1.375
0.65
0.902125
5.4555
6 0.8
0.472
0.95
0.104875
0.7125
7 1.1
-0.179
1.25
-0.35938
-2.0325
8 1.4
-0.416
1.55
-0.32863
-1.8075
9 1.7
-0.077
1.85
0.359125
2.3595
10
2
1
Для нахождения интеграла методом левых прямоугольников,
необходимо просуммировать элементы третьего ряда в диапазоне
90
÷
=
i
и умножить на шаг
3
,
0
=
h
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

76
Аналогично для формулы правых прямоугольников, суммировать
в диапазоне
101
÷
=
i
.
Сумма элементов пятого столбца, помноженная на шаг, даст
результат по формуле средних прямоугольников.
Согласно формуле трапеций, необходимо к полусумме первого и
последнего значения элементов третьего столбца добавить сумму всех
остальных членов этого столбца, и умножить результат на шаг
3
,
0
=
h
.
Суммируя значения последнего столбца и умножая ее на
6
h
=0,05,
найдем интеграл по методу Симпсона, результаты соберем в таблицу:
Формула левых прямоугольников 5.7225
Формула правых прямоугольников 4.8225
Формула средних прямоугольников
5.23875
Формула трапеций 5.2725
Формула Симпсона 5.25
Как следует из таблицы, для данной подынтегральной функции
формула левых прямоугольников дает приближенное значение с
избытком, а формула правых прямоугольников – с недостатком.
Хорошую точность дали метод трапеций и метод средних
прямоугольников.
Результаты различаются, поскольку значения известной
подынтегральной функции в методе средних были вычислены в
средних точках, а не получены путем интерполяции.
Метод Симпсона дал абсолютно точное значение интеграла.
Это связано с тем, что первообразная функция в данном примере
является полиномом четвертого порядка, для которых метод
Симпсона дает точное значение.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
77
ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Постановка задачи
Многие задачи науки и техники сводятся к решению
обыкновенных дифференциальных уравнений (ОДУ). ОДУ
называются такие уравнения, которые содержат одну или несколько
производных от искомой функции. В общем виде ОДУ можно
записать в виде:
(
)
(
)
0,...,,,, =
′′′
n
yyyyxF
, (5.1)
где
x
– независимая переменная,
(
)
i
y
-
i
-ая производная от искомой функции,
n
– порядок уравнения.
Общее решение ОДУ
n
-го порядка содержит
n
произвольных
постоянных
n
ccc ,...,,
21
, т.е. общее решение имеет вид
(
)
n
cccxy ,...,,,
21
ϕ
=
.
Для выделения единственного решения необходимо задать
n
дополнительных условий. В зависимости от способа задания
дополнительных условий существуют два различных типа задач:
задача Коши и краевая задача. Если дополнительные условия
задаются в одной точке, то такая задача называется задачей Коши.
Дополнительные условия в задаче Коши называются начальными
условиями. Если же дополнительные условия задаются в более чем
одной точке, т.е. при различных значениях независимой переменной,
то такая задача называется краевой. Сами дополнительные условия
называются краевыми или граничными.
Ясно, что при
1
=
n
можно говорить только о задачи Коши.
Примеры постановки задачи Коши:
( )
11,
32
== yyx
dx
dy
;
( ) ( )
01,11,
2
2
2
=
′
=+= yyxy
dx
dy
dx
yd
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

78
Примеры краевых задач:
( ) ( ) ( )
01,10,sin2
2
2
===−+ yyxy
dx
dy
dx
yd
( ) ( ) ( )
23,01,01,
2
2
3
3
==
′
=−+= yyy
dx
dy
dx
yd
xx
dx
yd
.
Решить такие задачи аналитически удается лишь для некоторых
специальных типов уравнений, поэтому применение приближенных
методов решения является необходимостью.
Приближенные методы решения задачи Коши для ОДУ
первого порядка
Требуется найти решение y(x) ОДУ первого порядка
( )
yxf
dx
dy
,=
(5.2)
на отрезке
[
]
n
xx ,
0
при условии
(
)
00
yxy
=
. (5.3)
Приближенное решение будем искать в узлах расчетной сетки
niihxx
i
,...,1,0,
0
=
+
=
с шагом
n
xx
h
n 0
−
=
.
Необходимо найти приближенные значения в узлах сетки y
i
=y(x
i
).
Результаты расчетов занесем в таблицу
i
x
0
x
1
x
…
n
x
i
y
0
y
1
y
…
n
y
Интегрируя уравнение на отрезке
[
]
1
,
+ii
xx
, получим
( )
∫
+
=−
+
1
,
1
i
i
x
x
ii
dxyxfyy
. (5.4)
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
79
Для того, чтобы найти все значения
i
y
, нужно каким-то образом
вычислить интеграл, стоящий в правой части (5.4).
Применяя различные квадратурные формулы, будем получать методы
решения задачи (5.2), (5.3) разного порядка точности.
Метод Эйлера
Если для вычисления интеграла в (5.4) воспользоваться
простейшей формулой левых прямоугольников первого порядка
( ) ( )
ii
x
x
yxhfdxyxf
i
i
,,
1
=
∫
+
,
то получим явную формулу Эйлера:
(
)
iiii
yxhfyy ,
1
+
=
+
,
1
,...,
1
,
0
−
=
n
i
. (5.5)
Явный метод Эйлера имеет первый порядок аппроксимации.
Реализация метода.
Поскольку
(
)
0000
,,, yxfyx
известны, применяя (5.5)
последовательно, определим все y
i
:
(
)
0001
, yxhfyy
+
=
,
(
)
1112
, yxhfyy
+
=
, ….
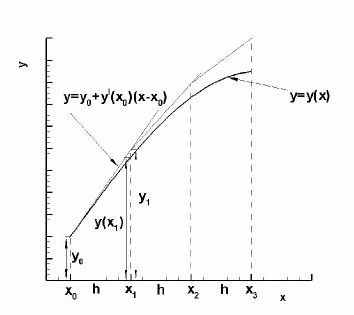
Геометрическая интерпретация метода Эйлера
(рис. 5.1.):
Пользуясь тем, что в точке
0
x
известно решение
(
)
00
yxy
=
и
значение его производной
( ) ( )
000
,
0
yxf
dx
dy
xy
xx
==
′
=
, можно записать
уравнение касательной к графику искомой функции
(
)
xyy
=
в точке
(
)
00
, yxf
:
(
)
(
)
0000
, xxyxfyy
−
+
=
.
При достаточно малом шаге
h
ордината
(
)
0001
, yxhfyy
+
=
этой
касательной, полученная подстановкой в правую часть значения
hxx
+
=
01
, должна мало отличаться от ординаты
(
)
1
xy
решения
(
)
xy
задачи Коши.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
80
Следовательно, точка
(
)
11
, yx
пересечения касательной с прямой
1
xx
=
может быть приближенно принята за новую начальную точку.
Через эту точку снова проведем прямую
(
)
(
)
1111
, xxyxfyy
−
+
=
,
которая приближенно отражает поведение касательной к
(
)
xy
в точке
(
)
(
)
11
, xyx
.
Подставляя сюда
hxx
+
=
12
(т.е. пересечение с прямой
2
xx
=
),
получим приближенное значение
(
)
xy
в точке
2
x
:
(
)
1112
, yxhfyy
+
=
и
т.д.
В итоге для
i
-ой точки получим формулу Эйлера.
Рис. 5.1. Геометрическая интерпретация метода Эйлера
Если в (5.4) использовать формулу правых прямоугольников:
( ) ( )
11
,,
1
++
=
∫
+
ii
x
x
yxhfdxyxf
i
i
,
то получим неявный метод Эйлера
(
)
111
,
+++
+
=
iiii
yxhfyy
,
1
,...,
1
,
0
−
=
n
i
. (5.6)
Этот метод называют неявным, поскольку для вычисления
неизвестного значения
(
)
11 ++
≈
ii
xyy
по известному значению
(
)
ii
xyy
≈
требуется решать уравнение, в общем случае нелинейное.
Неявный метод Эйлера также имеет первый порядок
аппроксимации.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
