Руев Г.А. и др. Методы вычислений и их реализация в Excel
Подождите немного. Документ загружается.


11
Приближенные (итерационные) методы решения НАУ
Пусть интервалы изоляции корней известны. Познакомимся с
несколькими итерационными методами, позволяющими найти корень
на известном интервале изоляции [a, b].
Метод деления отрезка пополам (дихотомии).
Идея метода заключается в делении отрезка, на котором
содержится корень, пополам, до тех пор, пока не будет достигнута
заданная точность.
Поделим отрезок
[
]
ba,
пополам. Координата середины отрезка
определится как
2
ba
c
+
=
. Теперь корень остался на одной из частей:
[
]
ca,
или
[
]
bc,
. Если
(
)
(
)
0
<
⋅
cfaf
, то это говорит о том, что функция
на отрезке
[
]
ca,
меняет свой знак, то есть на данном интервале
находится корень. В этом случае деление отрезка можно повторить,
приняв в качестве нового правого конца точку
c
, т.е. приравняв
cb
=
.
В противном случае, корень попал на половину
[
]
bc,
, и необходимо
изменить значение левого конца отрезка:
c
a
=
. Поскольку корень
всегда заключен внутри отрезка, итерационный процесс можно
останавливать, если длина отрезка станет меньше заданной точности:
ε
<−ab
.
ПРИМЕР 1.2.
Найдем первый корень уравнения
(
)
01136
23
=++−= xxxxf
с
точностью
05
,
0
=
ε
.
Вычисления выполним при помощи электронной таблицы Excel,
задавая начальные значения концов интервала изоляции и формул для
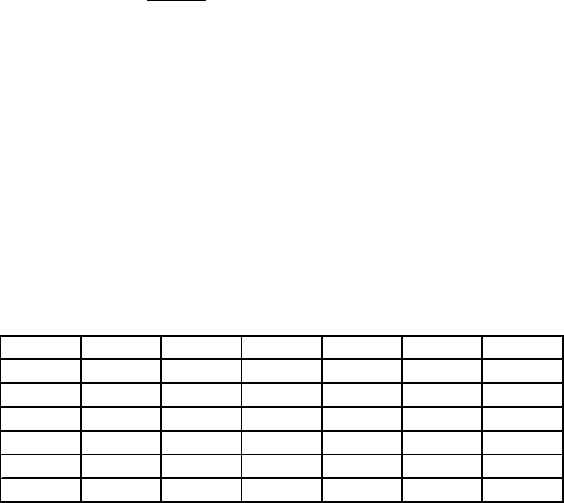
выполнения итераций. Результаты оформляются в виде таблицы
a b c f(a) f( c) |b-a|
1 -2 -1 -1.5 -27 -10.375 1
2 -1.5 -1 -1.25 -10.375 -4.078125 0.5
3 -1.25 -1 -1.125 -4.078125 -1.392578 0.25
4 -1.125 -1 -1.0625 -1.392578 -0.1604 0.125
5 -1.0625 -1 -1.03125 -0.1604 0.42868 0.0625
6 -1.0625 -1.03125 -1.046875 -0.1604 0.136372 0.03125
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
12
где во второй строке во втором и третьем столбцах заданы
0
a
,
0
b
–
начальные границы интервала изоляции корня;
c
вычисляется по
формуле
2
ii
i
ba
c
+
=
,
...3,2,1
=
i
, а
i
a
,
i
b
в свою очередь
определяются как
(
)
(
)
>⋅
=
−
−−−
случаепротивномвa
cfafеслиc
a
i
iii
i
,
;0,
1
111
и
(
)
(
)
>⋅
=
−
−−−
.,
;0,
1
111
случаепротивномвc
cfafеслиb
b
i
iii
i
В результате расчета приближенное значение первого корня
047,1
1
−≈x
при заданной величине точности
05,0
=
ε
. При
001,0
=
ε
необходимо сделать большее число итераций, поэтому к
приведенной выше таблице добавятся строки:
7 -1.0625 -1.04688 -1.05469 -0.1604 -0.01146 0.015625
8 -1.05469 -1.04688 -1.05078 -0.01146 0.062598 0.007813
9 -1.05469 -1.05078 -1.05273 -0.01146 0.025606 0.003906
10 -1.05469 -1.05273 -1.05371 -0.01146 0.007084 0.001953
11 -1.05469 -1.05371 -1.0542 -0.01146 -0.00218 0.000977
12 -1.0542 -1.05371 -1.05396 -0.00218 0.002451 0.000488
13 -1.0542 -1.05396 -1.05408 -0.00218 0.000134 0.000244
Как можно видеть, значение корня в этом случае
054,1
1
−
≈
x
, что
является более близким к точному значению. Второй и третий корни
находятся аналогично.
Метод простой итерации
Для метода простой итерации (МПИ) уравнение (1.1)
необходимо сначала преобразовать к виду
(
)
xx
ϕ
=
. Это всегда
можно сделать с помощью эквивалентных преобразований. Далее,
выберем начальное приближение
[
]
bax ,
0
∈
. Следующие итерации
производятся по формуле:
(
)
kk
xx
ϕ
=
+1
, т.е.
(
)
01
xx
ϕ
=
,
(
)
12
xx
ϕ
=
, и
т.д. Если последовательность
{
}
k
x
,
,...2,1
=
k
сходится, то
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
13
(
)
**
lim xxx
k
ϕ
==
, то есть в пределе получаем искомое решение
уравнения. Итерационный процесс следует остановить, когда
ε
<−
+ kk
xx
1
. В качестве начального приближения обычно берут
середину отрезка
[
]
ba,
:
2
0
ba
x
+
=
.
Привести исходное уравнение (1.1) к виду
(
)
xx
ϕ
=
можно
бесконечным числом способов. Из всевозможных функций ϕ(x)
выбирают ту, которая порождает сходящуюся к корню
последовательность
{
}
k
x
.
Достаточное условие сходимости. Пусть
(
)
x
ϕ
имеет
производную на отрезке
[
]
ba,
,
(
)
[
]
bax ,
∈
ϕ
и
(
)
1<≤
′
qx
ϕ
для всех
x
из отрезка
[
]
ba,
. Тогда итерационный процесс сходится к корню
уравнения, т.е.
*
lim xx
k
k
=
∞→
.
Доказательство. Из формулы МПИ следует, что
(
)
(
)
(
)
***
1
xxxxxx
kkk
ϕϕϕ
−=−=−
+
Применяя теорему Лагранжа о среднем, получим
(
)
(
)
(
)
***
xxqxxxx
kkk
−≤−
′
≤−
ξϕϕϕ
.
Аналогично
*
1
*
xxqxx
kk
−≤−
−
,
*
2
*
1
xxqxx
kk
−≤−
−−
и т.д.
Следовательно,
( )
abqxxq
xxqxxqxxqxx
kk
kkkk
−≤−≤
≤−≤−≤−≤−
−−+
*
0
*
2
3*
1
2**
1
...
Так как
1
<
q
, то
0lim =
∞→
k
k
q
и, следовательно,
*
lim xx
k
k
=
∞→
.
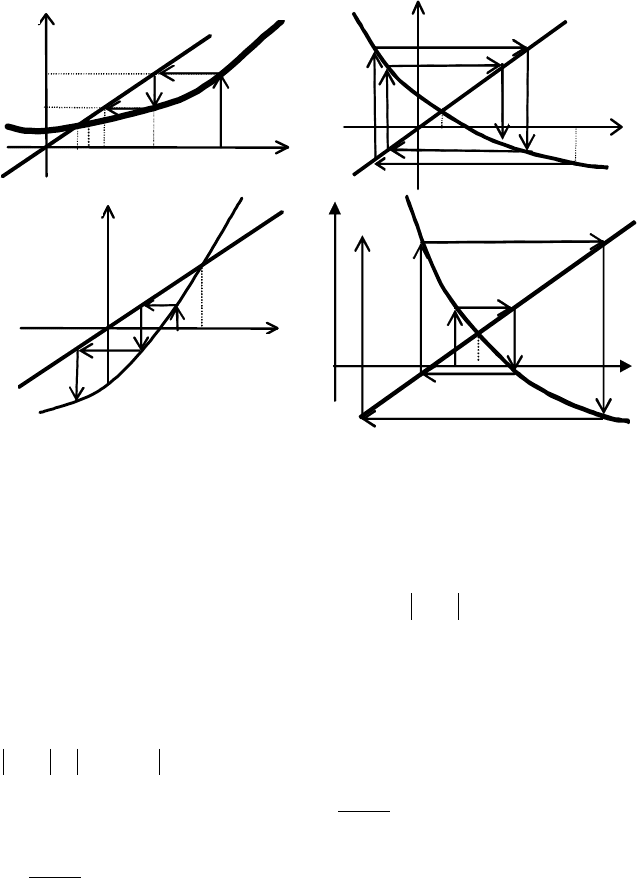
Геометрическая интерпретация метода простой итерации
представлена на рис. 1.4 для случаев
10
<
′
<
ϕ
(а),
1
−
<
′
ϕ
(б),
1
>
′
ϕ
(в) и
01
<
′
<
−
ϕ
(г).
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
14
y
y=x
x
x*
x
0
x
1
y=
ϕ
(x)
x
2
а
y=x
x
x*
x
0
x
1
y=
ϕ
(x)
x
3
x
2
x
4
б
y
y
y=x
x
x
0
x
1
y=
ϕ
(x)
x
2
в
x*
y=x
x
x*
x
0
x
1
y=
ϕ
(x)
x
3
x
2
x
4
г
y
Рис. 1.4. Сходящийся (а, б) и расходящийся (в, г) МПИ
Метод релаксации
На практике часто в качестве функции
(
)
x
ϕ
выбирают функцию
(
)
(
)
xcfxx −=
ϕ
, где
c
– некоторая постоянная. Постоянную
c
выбирают таким образом, чтобы условие
(
)
1<≤
′
qx
ϕ
выполнялось
бы для всех
[
]
bax ,∈
.
При таком выборе функции
(
)
x
ϕ
метод простой итерации
называют методом релаксации.
Получим условия на выбор константы
c
:
(
)
(
)
(
)
(
)
0211111 <
′
−<−⇒<
′
−<−⇒<
′
−=
′
xfcxfcxfcx
ϕ
Таким образом, если
(
)
0<
′
xf
, то
( )
0
2
<<
′
c
xf
. Если же
(
)
0>
′
xf
,
то
( )
0
2
>>
′
c
xf
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
15
Отсюда видно, что знак постоянной
c
совпадает со знаком
производной
(
)
xf
′
. Часто
c
берут в виде:
m
M
c
+
=
2
, где
(
)
(
)
xfM
′
= max
,
(
)
(
)
xfm
′
=min
.
Убедимся, что такой выбор
c
удовлетворяет условию
сходимости. Пусть
(
)
0>
′
xf
. Тогда
0
>
M
и
0
>
m
, и,
следовательно,
0
>
c
и
( )
(
)
(
)
( )( )
0
222
>
+
′
′
−
+
=
+
−
′
mMxf
xfmM
mMxf
, т.к.
(
)
xfM
′
>
.
Следовательно,
( )
0
2
>>
′
c
xf
.
Пусть теперь
(
)
0<
′
xf
. Тогда
0
<
M
,
0
<
m
0
<
⇒
c
и
( )
(
)
(
)
( )( )
0
222
>
+
′
−
−
′
=
′
−
+ mMxf
mMxf
xfmM
, т.к.
(
)
(
)
(
)
0,0 >−
′
>+
′
MxfmMxf
и
0
>
−
m
.
Следовательно,
( )
0
2
<<
′
c
xf
.
ПРИМЕР 1.3.
Найдем с точностью
001,0
=
ε
второй корень уравнения
(
)
01136
23
=++−= xxxxf
, лежащий на интервале
[
]
3,1
. Для
определения значения параметра
c
необходимо найти максимальное
и минимальное значения производной функции
(
)
xf
′
на отрезке
[
]
3,1
.
Для этого необходимо найти значения
(
)
xf
′
на концах интервала и в
точках экстремума, где
(
)
0=
′
′
xf
(если эти точки лежат на
исследуемом отрезке). Далее среди этих значений выбираются
максимальное и минимальное. В нашем случае
(
)
3123
2
+−=
′
xxxf
,
(
)
631231 −=+−=
′
f
(
)
6336273 −=+−=
′
f
,
(
)
0126 =−=
′
′
xxf
при
2
=
x
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

16
Экстремум производной находится на заданном отрезке
[
]
3,1
,
находим значение производной в этой точке:
(
)
9324122 −=+−=
′
f
. Следовательно
(
)
69,6,6max −=−−−=M
,
(
)
99,6,6min −=−−−=m
,
15
2
9
6
22
−=
−−
=
+
=
m
M
c
.
Таким образом,
( )
(
)
1136
15
2
23
++−+= xxxxx
ϕ
.
Выберем начальное приближение
2
2
31
0
=
+
=x
, следующие
приближения вычисляются по формуле
(
)
1136
15
2
23
1
++−+=
+ kkkkk
xxxxx
, k=0, 1, 2,..
Условием окончания итерационного процесса является условие:
001,0
1
=<−
+
ε
kk
xx
или
(
)
001,0<
k
xf
.
Результаты вычислений оформим на рабочем листе Excel в виде
таблицы:
A B C
1 Номер
итерации
k
x
kk
xx −
+1
2
0 2
3 1 2,133333 0,133333
4 2 2,106983 0,026351
5
3 2,1121 0,005117
6 4 2,111101 0,000999
7 5 2,111296 0,000195
Здесь формулы для вычисления
1
x
имеют вид:
=B2+2/15*(B2^3-
6*B2^2+3*B2+11), а для
1 0
x x
−
:
=ABS(B3-B2). Остальные вычисления получаются простым
копированием формул.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
17
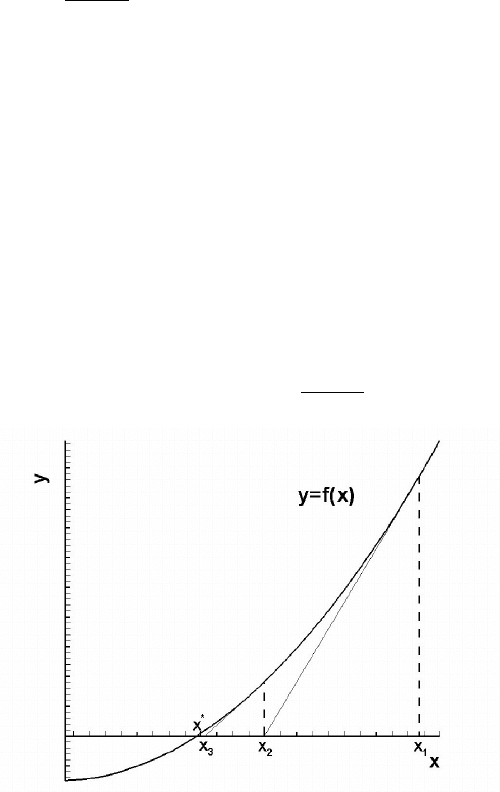
Метод Ньютона (касательных)
Для уравнений (1.1) метод Ньютона определяется формулой:
(
)
( )
k
k
kk
xf
xf
xx
′
−=
+1
. Суть метода состоит в замене нелинейной
функции f(x) линейной. Геометрическая иллюстрация метода
представлена на рис. 1.5.
Участок кривой
(
)
xfy =
на отрезке
[
]
1
,
+
∈
kk
xxx
заменяется
отрезком касательной, проведенной из точки
k
x
к графику функции
(
)
xfy =
.
Уравнение касательной имеет вид
(
)
(
)
(
)
kkk
xfxxxfy
′
−+=
.
Найдем точку пересечения касательной с графиком функции
0
=
y
,
т.е. с осью абсцисс, и обозначим ее
1+k
x
.
Тогда уравнение касательной в этой точке будет иметь вид
(
)
(
)
(
)
kkkk
xfxxxf
′
−+=
+1
0 .
Отсюда можно найти
(
)
( )
k
k
kk
xf
xf
xx
′
−=
+1
.
Рис. 1.5. Графическая интерпретация метода Ньютона
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

18
Можно показать, что
2
*
1
*
1
xxqxx
kk
−<−
++
,
т.е. метод сходится со вторым порядком.
Метод Ньютона можно трактовать как метод простой итерации,
если функцию
(
)
x
ϕ
выбрать в виде
( )
(
)
( )
xf
xf
xx
′
−=
ϕ
.
Замечание.
Если известен интервал изоляции, в котором
(
)
xf
′
′
не меняет
знак, то в качестве начального приближения берут тот конец
интервала изоляции, для которого знаки
(
)
xf
и
(
)
xf
′
′
совпадают.
ПРИМЕР 1.4.
Найдем с помощью метода Ньютона третий корень уравнения
01136
23
=++− xxx
, лежащий на интервале
[
]
5,4
, с точностью
001,0
=
ε
.
Сначала убедимся, что
(
)
xf
′
′
не меняет знака на этом отрезке.
(
)
126 −=
′
′
xxf
(
)
0>
′
′
xf
при
2
>
x
,
т.е.
(
)
0>
′
′
xf
на интервале [4,5].
Так как
(
)
015 >=f
,
то на этом конце знаки
(
)
xf
и
(
)
xf
′
′
совпадают и
5
0
=x
.
Вычисления оформим в виде таблицы:
Номер итерации
k
x
(
)
k
xf
(
)
k
xf
′
kk
xx −
+1
0 5 1 18
1 4.944444
0.027606
17.00926
0.055556
2 4.942821
2.33E-05 16.98059
0.001623
3 4.94282 1.66E-11 16.98057
1.37E-06
Здесь
(
)
1136
23
++−=
kkkk
xxxxf
,
(
)
3123
2
+−=
′
kkk
xxxf
,
(
)
( )
k
k
kk
xf
xf
xx
′
−=
+1
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
19
В качестве корня можно взять значение:
943,4
=
x
.
Из таблицы видно, что процесс сошелся уже на второй итерации.
Для того, чтобы сравнить методы дихотомии и касательных,
найдем первый корень уравнения
01136
23
=++− xxx
на отрезке
[
]
1,2 −−
методом Ньютона:
Так как
(
)
126 −=
′
′
xxf
,
то
(
)
0<
′
′
xf
на интервале
[
]
1,2 −−
,
а так как
(
)
0272 <−=−f
, то
2
0
−=x
.
Номер итерации
k
x
(
)
k
xf
(
)
k
xf
′
kk
xx −
+1
0 -2 -27 39 -
1 -1.30769
-5.41966
23.82249
0.692308
2 -1.08019
-0.50182
19.46272
0.227502
3 -1.05441
-0.00613
18.9882 0.025783
4 -1.05408
-9.5E-07 18.98229
0.000323
Заданная точность достигается на 4-ой итерации.
Напомним, что метод дихотомии (Пример 1.2) достиг точности
0,001 лишь на 10-ой итерации.
Вычислим второй корень нашего уравнения на отрезке
[
]
3,1
.
Поскольку вторая производная
(
)
126 −=
′
′
xxf
меняет знак на
отрезке
[
]
3,1
при
2
=
x
, уменьшим интервал изоляции так, чтобы
изменения знака не происходило.
Рассмотрим интервал
[
]
3;1,2
.
Вычислим значения функции и второй производной на левом
конце отрезка:
(
)
06,01,2 >=
′
′
f
,
(
)
0101,01,2 >=f
.
Поскольку функция и вторая производная имеют один знак, в качестве
начального приближения выбираем
1,2
0
=x
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

20
Номер
итерации
k
x
(
)
k
xf
(
)
k
xf
′
kk
xx −
+1
0 2.1 0.101 -8.97 -
1 2.11126 3.95E-05 -8.96286 0.01126
2 2.111264
6.47E-12 -8.96286 4.4E-06
3 2.111264
0 -8.96286 7.22E-13
В сравнении с методом простой итерации значение корня было
получено за две итерации вместо шести.
Эти примеры показывают, что метод Ньютона сходится быстрее,
чем метод дихотомии и метод простой итерации. Но для его
использования необходимо выбирать начальное приближение,
достаточно близкое к корню.
Упрощенный метод Ньютона.
Эта модификация метода Ньютона используется, если
производная
(
)
xf
′
представляет собой сложную функцию, и для ее
вычисления на каждой итерации тратится много времени.
Зададим
0
x
– начальное приближение и вычислим производную
(
)
0
xfz
′
=
. На следующих итерациях используется вычисленное
значение производной:
(
)
z
xf
xx
k
kk
−=
+1
.
Это упрощение несколько замедляет процесс сходимости к
решению, однако сокращает время каждого итерационного цикла.
Метод хорд
В этом методе кривая
(
)
xf
заменяется прямой линией – хордой,
стягивающей точки
(
)
(
)
afa,
и
(
)
(
)
bfb,
.
В зависимости от знака выражения
(
)
(
)
afaf
′
′
метод хорд имеет
два варианта, изображенных на рис. 1.6, а, б.
Пусть
(
)
(
)
0>
′
′
afaf
(рис. 1.6, а). Тогда bx =
0
, точка
a
будет
оставаться неподвижной.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
