Руев Г.А. и др. Методы вычислений и их реализация в Excel
Подождите немного. Документ загружается.

41
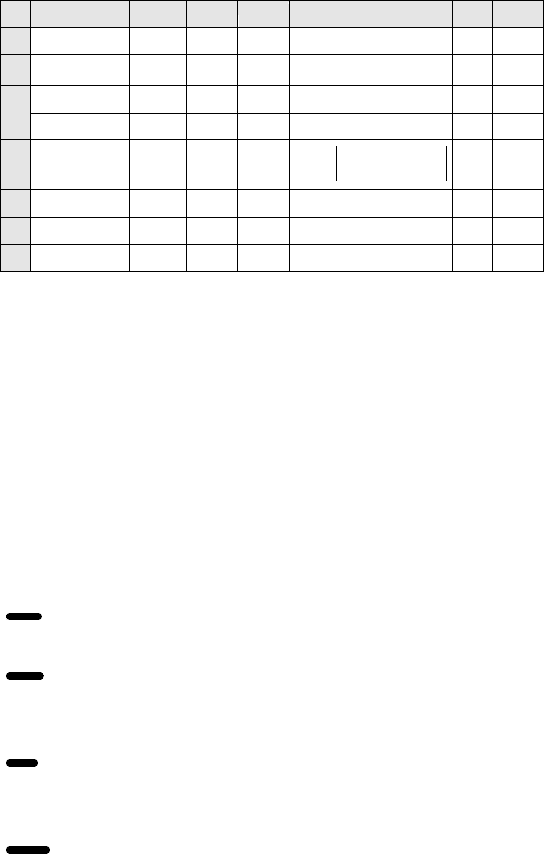
Занесем исходные данные на рабочий лист.
A B C D E F G
1
0 -0,5
-0,25
1,25
2
α
=
-0,6
0 -0,2
β
=
1
3
-0,3
0,2 0 0,4
4
5
номер
итерации
(
)
k
x
1
(
)
k
x
2
(
)
k
x
3
(
)
(
)
k
i
k
i
i
xx −
+1
max
6
0 0 0 0 -
7
1 1.25
1 0.4 1.25
8
2
Выделим ячейки B7:D7 и введем формулу (2.9):
{=МУМНОЖ($B$1:$D$3;ТРАНСП(B6:D6))+ТРАНСП($G$1:$G$3)}.
Остальные формулы для вычисления
(
)
k
i
x
получаются
копированием.
Метод Гаусса-Зейделя
В отличие от метода Якоби, в котором вычисления всех
компонент вектора
(
)
1+k
-го приближения проводилось однообразно,
в методе Гаусса-Зейделя для расчета
i
-й компоненты следующего
приближения используется уже вычисленное на этом, т.е.
(
)
1
+
k
-м
шаге, новые значения первых
1
−
i
компонент:
( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )
( )
1
11,
1
22
1
11
1
211,
1
11,
1
22
1
11
1
2323
1
1212
22
1
2
13132121
11
1
1
...
1
...
......
1
...
...
1
...
1
+
−−
+++
++
+
−−
+++
++
+
−−−−=
−−−−−−−=
−−−−=
−−−−=
k
mmm
k
m
k
mm
mm
k
m
k
mm
k
iii
k
iii
k
i
k
ii
ii
k
i
k
mm
kkk
k
mm
kkk
xaxaxaf
a
x
xaxaxaxaxaf
a
x
xaxaxaf
a
x
xaxaxaf
a
x
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

42
Или, в компактном виде:
( ) ( ) ( )
−−=
∑∑
+=
−
=
++
m
ij
k
jij
i
j
k
jiji
ii
k
i
xaxaf
a
x
1
1
1
11
1
, i=1, 2, …, m. (2.12)
Достаточное условие сходимости этого метода, как и для методы
Якоби, является условие диагонального преобладания:
∑
≠
=
>
m
ji
j
ijii
aa
1
,
m
i
,...,
2
,
1
=
.
ПРИМЕР 2.6.
Найдем решение СЛАУ из Примера 2.4 методом Гаусса-Зейделя.
=+−
=++
=++
41023
553
10248
321
321
321
xxx
xxx
xxx
.
Расчетные формулы:
(
)
(
)
(
)
( ) ( ) ( )
( ) ( ) ( )
1
2
1
1
1
3
3
1
1
1
2
32
1
1
2,03,04,0
2,06,01
25,05,025,1
+++
++
+
+−=
−−=
−−=
kkk
kkk
kkk
xxx
xxx
xxx
.
Таблица итераций выглядит в данном случае следующим образом:
Номер
итерации
(
)
k
x
1
(
)
k
x
2
(
)
k
x
3
(
)
(
)
k
i
k
i
i
xx −
+1
max
0 0 0 0
1 1.25 0.25 0.075 1.25
2 1.10625 0.32125 0.132375
0.14375
3 1.056281
0.339756
0.151067
0.049969
4 1.042355
0.344374
0.156168
0.013926
5 1.038771
0.345504
0.157469
0.003584
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

43
Здесь
(
)
( )
( )
075,025,02,025,13,04,0
25,002,025,16,01
25,1025,005,025,1
1
3
1
2
1
1
=⋅+⋅−=
=⋅−⋅−=
=⋅−⋅−=
x
x
x
,
( ) ( )
( ) ( )
( ) ( )
01,025,1
075,0
25,0
25,1
max
0
3
1
3
0
2
1
2
0
1
1
1
=>=
=
−
−
−
ε
xx
xx
xx
(
)
( )
( )
132,032125,02,010625,13,04,0
32125,0075,02,010625,16,01
10625,1075,025,025,05,025,1
2
3
2
2
2
1
=⋅+⋅−=
=⋅−⋅−=
=⋅−⋅−=
x
x
x
,
( ) ( )
( ) ( )
( ) ( )
01,014375,0
057375,0
07125,0
14375,0
max
1
3
2
3
1
2
2
2
1
1
2
1
=>=
=
−
−
−
ε
xx
xx
xx
и т.д.
Из таблицы видно, что нужная точность достигнута уже на 5-ой
итерации вместо 11-ой по методу простой итерации.
При реализации в Excel расчетные формулы для
(
)
1
i
x
примут вид:
(
)
1
1
x
=1/$B$1*($G$1-$C$1*C6-$D$1*D6),
(
)
1
2
x
=1/$C$2*($G$2-$B$2*B7-$D$2*D6),
(
)
1
3
x
=1/$D$3*($G$3-$B$3*B7-$C$3*C7).
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
44
АППРОКСИМАЦИЯ ФУНКЦИЙ
Слово «аппроксимация» происходит от латинского approximo —
приближаюсь.
Аппроксимировать – это означает приближенно заменить. Задачи
интерполяции возникают при обработке результатов экспериментов,
когда измерения какой-либо величины выполнены в конечном числе
точек. Требуется найти промежуточные значения этой функции. Это
так называемая задача о восстановлении функции. Кроме того, при
проведении расчетов сложные функции удобно заменять
(аппроксимировать) алгебраическими многочленами или другими
элементарными функциями, которые достаточно просто вычисляются
(задача о приближении функции). Методы интерполяции
используются для приближенного интегрирования и решения
дифференциальных уравнений, а также являются основой
компьютерной графики и других современных цифровых технологий.
Постановка задачи интерполяции
На интервале
[
]
ba,
заданы точки
i
x
,
N
i
,...,
1
,
0
=
;
bxa
i
≤
≤
, и
значения неизвестной функции в этих точках
(
)
ii
fxf
=
,
Ni ,...,1,0
=
.
Требуется найти функцию
(
)
xF
,
принимающую в точках
i
x
те же значения
i
f
.
Точки
i
x
будем называть узлами интерполяции,
а условия
(
)
ii
fxF
=
– условиями интерполяции.
При этом
(
)
xF
будем искать только на отрезке
[
]
ba,
.
Если необходимо найти функцию вне отрезка, то такая задача
называется задачей экстраполяции.
Мы будем рассматривать только задачи интерполяции.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
45
Поставленная задача имеет много решений, т.к. через заданные
точки
(
)
ii
fx ,
,
N
i
,...,
1
,
0
=
, можно провести бесконечно много кривых,
каждая из которых будет графиком функции, для которой выполнены
все условия интерполяции. Для практики важен случай
аппроксимации функции многочленами, т.е.
(
)
m
m
xaxaxaaxF ++++= ...
2
210
,
где
i
a
– постоянные коэффициенты.
Все методы интерполяции можно разделить на локальные и
глобальные.
В случае локальной интерполяции на каждом интервале
[
]
ii
xx ,
1−
строится отдельный полином.
В случае глобальной интерполяции отыскивается единый
полином на всем интервале
[
]
ba,
. При этом искомый полином
называется интерполяционный полиномом.
Локальная интерполяция
Кусочно-постоянная интерполяция
При кусочно-постоянной интерполяции интерполяционный
многочлен на каждом отрезке
[
]
ii
xx ,
1−
равен константе, а именно,
левому или правому значению функции.
Для левой кусочно-постоянной интерполяции
(
)
1−
=
i
fxF
, если
ii
xxx
<
≤
−1
, т.е.
( )
<≤
<≤
<≤
=
−− NNN
xxxf
xxxf
xxxf
xF
11
211
100
,
...
,
,
.
Для правой кусочно-постоянной интерполяции
(
)
i
fxF
=
, если
ii
xxx
≤
<
−1
, т.е.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
46
( )
≤<
≤<
≤<
=
− NNN
xxxf
xxxf
xxxf
xF
1
212
101
,
...
,
,
.
Легко понять, что при таком выборе функции
(
)
xF
условия
интерполяция выполняются. Однако, построенная функция является
разрывной, что ограничивает ее применение.
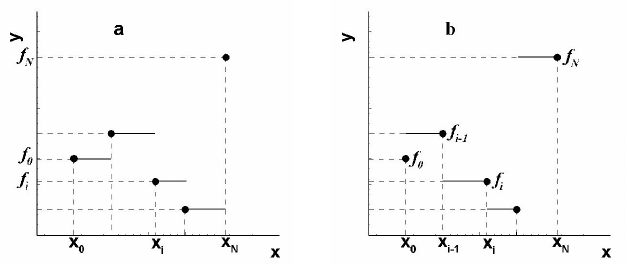
Графическое представление для кусочно-постоянной
интерполяции можно увидеть на рис. 3.1.
Рис. 3.1. Левая (а) и правая (б) кусочно–постоянная интерполяции
Кусочно-линейная интерполяция
На каждом интервале
[
]
ii
xx ,
1−
интерполирующая функция
является линейной
(
)
iii
lxkxF
+
=
.
Значения коэффициентов
i
k
и
i
l
находятся из выполнения
условий интерполяции на концах отрезка
[
]
ii
xx ,
1−
:
(
)
11 −−
=
iii
fxF
,
(
)
iii
fxF
=
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

47
С помощью этих условий получаем систему уравнений:
=+
=+
−−
iiii
iiii
flxk
flxk
11
, откуда находим
1
1
−
−
−
−
=
ii
ii
i
xx
ff
k
,
i
ii
ii
ii
x
xx
ff
fl
1
1
−
−
−
−
−=
.
Следовательно, функцию
(
)
xF
можно записать в виде:
( ) ( )
ii
ii
ii
fxx
xx
ff
xF +−
−
−
=
−
−
1
1
,
если
ii
xxx
≤
≤
−1
, т.е.
( )
( )
( )
( )
≤≤+−
−
−
≤≤+−
−
−
≤≤+−
−
−
=
−−−
−
−
NNNN
NN
NN
xxxfxx
xx
ff
xxxfxx
xx
ff
xxxfxx
xx
ff
xF
111
11
1
2111
12
12
1000
01
01
,
...
,
,,
.
При использовании линейной интерполяции сначала нужно
определить интервал, в который попадает значение
x
, а затем
подставить его в формулу.
Итоговая функция является непрерывной, но ее производная
разрывна в каждом узле интерполяции.
Погрешность такой интерполяции будет меньше, чем в случае
кусочно-постоянной интерполяции.
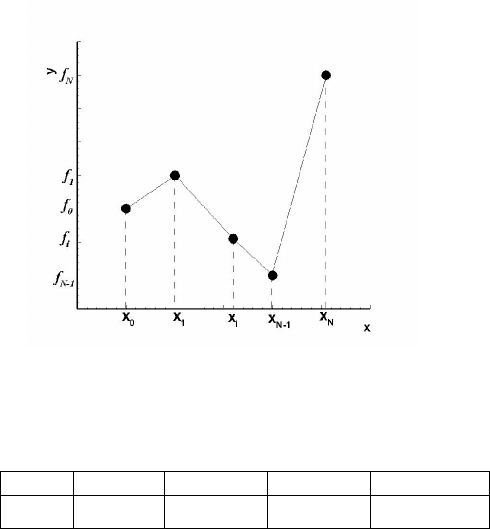
Иллюстрация кусочно-линейной интерполяции приведена на рис.
3.2.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
48
Рис. 3.2. Кусочно-линейная интерполяция
ПРИМЕР 3.1
Заданы значений некоторой функции:
x
0 2 3 3,5
f
-1 0.2 0,5 0,8
Требуется найти значение функции при
1
=
z
и
2
,
3
=
z
при
помощи кусочно-постоянной и кусочно-линейной интерполяции.
Решение.
Точка
1
=
z
принадлежит первому отрезку
[
]
2,0
, т.е.
1
=
i
и,
следовательно,
по формулам левой кусочно-постоянной интерполяции
(
)
11
0
−
=
=
fF
,
по формулам правой кусочно-постоянной интерполяции
(
)
2,01
1
=
=
fF
.
Теперь воспользуемся формулами кусочно-линейной
интерполяции:
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
49
6,0
2
12,0
01
01
1
=
+
=
−
−
=
xx
ff
k
,
12
2
2,1
2,0
1
00
01
11
−=−=
−
−
−= x
xx
ff
fl
,
и тогда
(
)
(
)
4,0116,01
−
=
−
=
F
.
Точка
2
,
3
=
z
принадлежит третьему интервалу
[
]
5,3;3
,
т.е.
3
=
i
и, следовательно,
по формулам левой кусочно-постоянной интерполяции
(
)
5,02,3
2
=
=
fF
,
по формулам правой кусочно-постоянной интерполяции
(
)
8,02,3
3
=
=
fF
.
Воспользуемся формулами кусочно-линейной интерполяции:
6,0
35,3
5,08,0
23
23
3
=
−
−
=
−
−
=
xx
ff
k
,
3,15,36,08,0
3
23
23
33
−=⋅−=
−
−
−= x
xx
ff
fl
, и
(
)
(
)
62,03,12,36,02,3
=
−
=
F
.
Кубический интерполяционный сплайн
Слово сплайн, происходящее от английского слова spline,
означает гибкую линейку, используемую для проведения гладких
кривых через заданные точки на плоскости. Форма этого
универсального лекала на каждом отрезке описывается кубической
параболой. Сплайны широко используются в инженерных
приложениях, в частности, в компьютерной графике, поскольку
позволяют с хорошей точностью задать кривые в виде нескольких
массивов коэффициентов.
Итак, на каждом
i
-м отрезке
[
]
ii
xx ,
1−
,
N
i
,...,
2
,
1
=
, решение будем
искать в виде полинома третьей степени:
( ) ( )
(
)
(
)
6
2
32
i
i
i
iiiii
xx
d
xx
cxxbaxS
−
+
−
+−+=
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

50
Неизвестные коэффициенты
iiii
dcba ,,,
,
N
i
,...,
2
,
1
,
0
=
, находим из:
• условий интерполяции:
(
)
iii
fxS
=
,
N
i
,...,
2
,
1
=
,
(
)
001
fxS
=
;
• непрерывности функции
(
)
(
)
111 −−−
=
iiii
xSxS
,
N
i
,...,
3
,
2
=
;
• непрерывности первой и второй производной:
(
)
(
)
111 −−−
′
=
′
iiii
xSxS
,
(
)
(
)
111 −−−
′
′
=
′
′
iiii
xSxS
,
N
i
,...,
3
,
2
=
.
Учитывая, что
( ) ( )
(
)
(
)
6
2
3
1
1
2
1
11111
−
−
−
−−−−−
−
+
−
+−+=
i
i
i
iiiii
xx
d
xx
cxxbaxS
,
для определения
N4
неизвестных
получаем систему
24
−
N
уравнений:
ii
fa
=
,
N
i
,...,
2
,
1
=
;
1
32
6
2
−
−=+−
ii
i
i
i
iii
ff
h
d
h
chb
,
N
i
,...,
2
,
1
=
;
2
2
1
ii
iiii
hd
hcbb −=−
−
,
N
i
,...,
2
,
1
=
;
1−
−
=
iiii
cchd
,
N
i
,...,
3
,
2
=
, где
1−
−
=
iii
xxh
.
Недостающие два уравнения выводятся из дополнительных
условий:
(
)
(
)
0
=
′
′
=
′
′
bSaS
.
Можно показать, что при этом
0
0
=
=
N
cc
.
Из системы можно исключить неизвестные
i
b
,
i
d
, получив
систему
1
+
N
линейных уравнений (СЛАУ) для определения
коэффициентов
i
c
:
0
0
=
c
,
0
=
N
c
,
( )
−
−
−
=+++
−
−+
+++−
1
11
1111
62
i
ii
i
ii
iiiiiii
h
ff
h
ff
chchhch
,
1
,...,
2
,
1
−
=
N
i
(3.1)
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
