Руев Г.А. и др. Методы вычислений и их реализация в Excel
Подождите немного. Документ загружается.

31
Разделив первую строку на главный элемент, как и прежде,
исключают
1
x
из остальных уравнений.
Затем для оставшихся столбцов и строк выбирают второй
главный элемент и т.д.
ПРИМЕР 2.4.
Рассмотрим применение метода Гаусса с выбором главного
элемента на примере следующей системы уравнений:
=+
=−+
=+
− 6
5
45,0
2
3
32
32
1
1
x
xx
xx
x
x
.
В первом уравнении коэффициент при
1
x
равен 0,
во втором 1 и в третьем -2,
т.е. максимальный по модулю коэффициент находится в третьем
уравнении.
Поэтому переставим третье уравнение на место первого:
=+
=−+
=+−
45,0
5
62
32
32
3
1
1
xx
xx
x
x
x
.
В третьем уравнении коэффициент при
1
x
равен 0.
Исключим
1
x
из второго уравнения:
=+
=−
=+−
45,0
85,0
62
32
32
31
xx
xx
xx
Рассмотрим второе и третье уравнения.
Исключим
2
x
из третьего уравнения.
Для этого умножим второе на -0.5 и сложим с третьим:
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
32
=
=−
=+−
025,1
85,0
62
3
32
31
x
xx
xx
.
Далее находим значения
i
x
обратным ходом:
из третьего уравнения получаем
0
3
=
x
,
из второго
8
2
=
x
, и из первого
3
1
−
=
x
.
Выполним проверку:
( )
=+
=−+
=+⋅
−−
−
60
508
4085,0
32
3
.
Такая перестановка уравнений необходима для того, чтобы
уменьшить влияние ошибок округления на конечный результат.
Часто возникает необходимость в решении СЛАУ, матрицы
которых являются слабо заполненными, т.е. содержат много нулевых
элементов. В то же время эти матрицы имеют определенную
структуру.
Среди таких систем выделим системы с матрицами ленточной
структуры, в которых ненулевые элементы располагаются на главной
диагонали и на нескольких побочных диагоналях. Для решения
систем с ленточными матрицами коэффициентов вместо метода
Гаусса можно использовать более эффективные методы.
Для случая трехдиагональных матриц разработан экономичный
метод прогонки.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
33
Метод прогонки
Рассмотрим метод прогонки для СЛАУ вида:
=−
−==+−
=+−
−
+−
nnnnn
iiiiiii
fxcxa
nifxbxcxa
fxbxc
1
11
12111
1,...,2,
(2.6)
Решение данной системы ищем в виде:
nixx
iiii
,...3,2,
111
=+=
−−−
βα
(2.7)
Здесь α
i
, β
i
– неизвестные прогоночные коэффициенты.
Как и метод Гаусса, метод прогонки состоит из двух этапов.
На первом (прямом) этапе определяются прогоночные
коэффициенты, на втором (обратном) вычисляется вектор решения.
Прямой этап.
Сравнивая соотношение (2.7) при i=2:
1211
βα
+= xx
и следствие первого уравнения системы (2.6):
1
1
2
1
1
1
c
f
x
c
b
x −=
,
получим формулы для первых прогоночных коэффициентов:
1
1
1
1
1
1
,
c
f
c
b
−==
βα
.
Подставляя (2.7) во второе уравнение (2.6), получим:
(
)
iiiiiiiii
fxbxcxa
=
+
−
+
+−− 111
β
α
.
Или, после преобразования,
(
)
iiiiiiiii
fxbaxca
=
+
+
−
+−− 111
β
α
,
откуда
1
1
1
1 −
−
+
−
−
−
−
−
=
iii
iii
i
iii
i
i
ac
af
x
ac
b
x
α
β
α
Сравнивая с (2.7), получим
1
1
1
,
−
−
−
−
−
−=
−
=
iii
iii
i
iii
i
i
ac
af
ac
b
α
β
β
α
α
.
Таким образом, можно найти все
1,...,1,,
−
=
ni
ii
β
α
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
34
Обратный этап.
Подставляя последнее прогоночное соотношение (2.7) в
последнее уравнение (2.6), получим:
(
)
1
1
11
−
−
−−
−
−
−=
=
−
+
nnn
nnn
n
nnnnnnn
ac
af
x
fxcxa
α
β
β
α
.
Затем, последовательно применяя (2.7), находим:
1211
2122
111
...
βα
βα
β
α
+=
+=
+
=
−−−−
−−−
xx
xx
xx
nnnn
nnnn
.
Таким образом, алгоритм метода прогонки можно представить в виде:
1. Находим
1
1
1
1
1
1
,
c
f
c
b
−==
βα
;
2. Для
1
,...,
1
−
=
n
i
вычисляем
1
1
1
,
−
−
−
−
−
−=
−
=
iii
iii
i
iii
i
i
ac
af
ac
b
α
β
β
α
α
.
3. Находим
1
1
−
−
−
−
−=
nnn
nnn
n
ac
af
x
α
β
.
4. Для
1
,...,
1
−
=
n
i
находим:
iiii
xx
β
α
+
=
+1
.
Теорема.
Пусть коэффициенты
i
a
,
i
b
системы уравнений при
1
,...,
3
,
2
−
=
n
i
отличны от нуля и пусть
iii
abc +≥
при
n
i
,...,
2
,
1
=
.
Тогда прогонка корректна и устойчива.
При выполнении этих условий знаменатели в алгоритме метода
прогонки не обращаются в нуль и, кроме того, погрешность
вычислений, внесенная на каком либо шаге расчетов, не будет
возрастать при переходе к следующим шагам. Данное условие есть не
что иное, как условие диагонального преобладания.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

35
Итерационные методы решения линейных алгебраических
систем
Метод простой итерации
Преобразуем исходную систему линейных уравнений
fx
r
r
=A
к
эквивалентной системе вида:
β
r
r
r
+= xx α
, (2.8)
где
x
r
– искомый вектор,
α
и
β
r
– некоторые новые матрица и вектор, соответственно.
Будем решать (2.8) методом последовательных приближений.
В качестве нулевого приближения можно взять
(
)
0
0
i
x
=
.
Следующее приближение находим по рекуррентным формулам
(
)
(
)
...,2,1,0,
1
=+=
+
kxx
kk
β
r
r
r
α
(2.9)
Такой итерационный процесс будем называть методом простых
итераций (МПИ). Так же, как и в случае МПИ для решения
нелинейных алгебраических уравнений, метод (2.9) сходится не для
любой матрицы
α
.
Достаточным условием сходимости МПИ (2.9) к решению системы
(2.8) при любом начальном векторе
(
)
0
x
r
является требование
1<α
,
где
∑
=
≤≤
=
n
j
ij
ni
1
1
max
α
α
– норма матрицы
α
.
Существует несколько способов построения порождающей
матрицы
α
, для которой выполняется достаточное условие
сходимости.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
36
Метод Якоби
Предположим, что диагональные элементы матрицы
A
исходной
системы не равны нулю (
0
≠
ii
a
,
m
i
,...,
2
,
1
=
). Разрешим первое
уравнение системы относительно
1
x
, второе относительно
2
x
и т.д.
Получим следующую эквивалентную систему, записанную в
скалярном виде:
( )
( )
( )
11,2211
23231212
22
2
13132121
11
1
...
1
...
...
1
...
1
−−
−−−−=
−−−−=
−−−−=
mmmmmm
mm
m
mm
mm
xaxaxaf
a
x
xaxaxaf
a
x
xaxaxaf
a
x
. (2.10)
Зададим вектор нулевого приближения
(
)
0
i
x
.
Следующие приближение будем вычислять по рекуррентным
соотношениям
( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )
( )
k
mmm
k
m
k
mm
mm
k
m
k
mm
kkk
k
mm
kkk
xaxaxaf
a
x
xaxaxaf
a
x
xaxaxaf
a
x
11,2211
1
23231212
22
1
2
13132121
11
1
1
...
1
...
...
1
...
1
−−
+
+
+
−−−−=
−−−−=
−−−−=
(2.11)
В свернутом виде данную систему можно переписать как
( ) ( )
−=
∑
≠
=
+
m
ij
j
k
jiji
ii
k
i
xaf
a
x
1
1
1
, i=1, 2, …, m.
Условием окончания итерационного процесса служит условие
(
)
(
)
ε
<−
++ 11
max
k
i
k
i
i
xx
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
37
Достаточное условие сходимости.
Метод Якоби является вариантом МПИ, в котором
mi
a
f
ji
ji
a
a
ii
i
i
ii
ij
ij
...,,2,1,,
,0
,
==
=
≠−
=
βα
Если для исходной матрицы A выполнено условие диагонального
преобладания, т.е.
∑
≠
=
>
m
ji
j
ijii
aa
1
,
m
i
,...,
2
,
1
=
, то выполняется условие
1<α
, т.е. итерационный процесс (2.11) сходится при любом выборе
начального приближения.
Если исходная система уравнений не удовлетворяет условию
сходимости, то ее приводят к виду с диагональным преобладанием.
Выбор начального приближения влияет на количество итераций,
необходимых для получения приближенного решения. Чаще всего в
качестве начального приближения берут
( )
ii
i
ii
a
f
x ==
β
0
или
(
)
0
0
=
i
x
.
Замечание.
Указанное выше условие сходимости является достаточным, т.е.
если оно выполняется, то процесс сходится. Но данное условие не
является необходимым, процесс может сходиться и при отсутствии
диагонального преобладания.
ПРИМЕР 2.5.
Решить СЛАУ из Примера 2.3 с помощью метода Якоби с
точностью
01
,
0
=
ε
.
С помощью прямого метода обратной матрицы найдено решение
038,1
1
=
x
,
346,0
2
=
x
,
158,0
2
=
x
.
Найдем решение методом Якоби.
Для начала проверим условие диагонального преобладания:
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
38
3210
135
248
+>
+>
+>
Приводим систему уравнений к виду (2.8):
( )
( )
( )
213
312
321
234
10
1
35
5
1
2410
8
1
xxx
xxx
xxx
+−=
−−=
−−=
или
213
312
321
2,03,04,0
2,06,01
25,05,025,1
xxx
xxx
xxx
+−=
−−=
−−=
.
Тогда
(
)
(
)
(
)
( ) ( ) ( )
( ) ( ) ( )
kkk
kkk
kkk
xxx
xxx
xxx
21
1
3
31
1
2
32
1
1
2,03,04,0
2,06,01
25,05,025,1
+−=
−−=
−−=
+
+
+
В качестве начального приближения выберем
(
)
0
0
=
i
x
.
Дальнейшие вычисления оформим в виде таблицы:
Номер
итерации
(
)
k
x
1
(
)
k
x
2
(
)
k
x
3
(
)
(
)
k
i
k
i
i
xx −
+1
max
0 0 0 0 -
1 1.25 1 0.4 1.25
2 0.65 0.17 0.225 0.83
3 1.10875 0.565 0.239 0.45875
4 0.90775 0.28695 0.180375
0.27805
5 1.061431
0.419275
0.185065
0.153681
6 0.994096
0.326128
0.165426
0.093147
7 1.045579
0.370457
0.166997
0.051483
8 1.023022
0.339253
0.160418
0.031204
9 1.040269
0.354103
0.160944
0.017247
10 1.032712
0.34365 0.15874 0.010453
11 1.03849 0.348625
0.158916
0.005778
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
39
Здесь
(
)
( )
( )
4,0
1
25,1
1
3
1
2
1
1
=
=
=
x
x
x
,
( ) ( )
( ) ( )
( ) ( )
01,025,1
4,0
1
25,1
max
0
3
1
3
0
2
1
2
0
1
1
1
=>=
=
−
−
−
ε
xx
xx
xx
,
(
)
( )
( )
225,012,025,13,04,0
17,04,02,05,16,01
65,04,025,015,025,1
2
3
2
2
2
1
=⋅+⋅−=
=⋅−⋅−=
=⋅−⋅−=
x
x
x
,
( ) ( )
( ) ( )
( ) ( )
01,083,0
175,0
83,0
6,0
max
1
3
2
3
1
2
2
2
1
1
2
1
=>=
=
−
−
−
ε
xx
xx
xx
,
(
)
( )
( )
239,017,02,065,03,04,0
565,0225,02,065,06,01
10875,1225,025,017,05,025,1
3
3
3
2
3
1
=⋅+⋅−=
=⋅−⋅−=
=⋅−⋅−=
x
x
x
,
( ) ( )
( ) ( )
( ) ( )
01,045875,0
014,0
395,0
45675,0
max
2
3
3
3
2
2
3
2
2
1
3
1
=>=
=
−
−
−
ε
xx
xx
xx
, и т.д.
Процесс продолжается, пока погрешность не станет меньше
01
,
0
, что
происходит на 11-ой итерации.
Следовательно,
приближенное решение имеет вид:
03849,1
1
=
x
,
348625,0
2
=
x
,
158916,0
3
=
x
,
что с точностью ε совпадает с решением, полученным по методу
обратной матрицы.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
40
При реализации в Excel расчетные формулы для
(
)
1
i
x
, при
условии, что исходные данные введены в лист Excel, как показано
ниже,
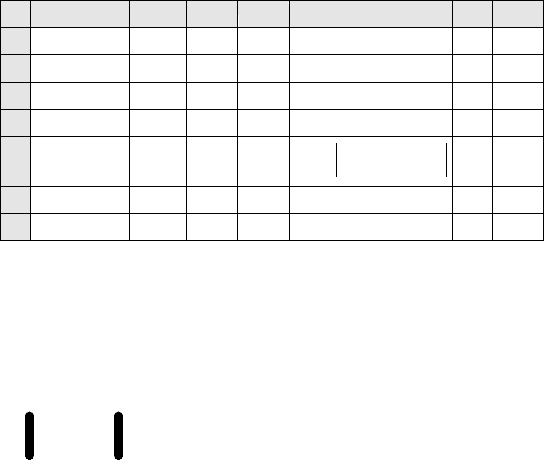
A B C D E F G
1
8 4 2 10
2
A= 3 5 1 f= 5
3
3 -2 10 4
4
5
номер
итерации
(
)
k
x
1
(
)
k
x
2
(
)
k
x
3
(
)
(
)
k
i
k
i
i
xx −
+1
max
6
0 0 0 0 -
7
1 1.25
1 0.4 1.25
имеют вид:
(
)
1
1
x
=1/$B$1*($G$1-$C$1*C6-$D$1*D6),
(
)
1
2
x
=1/$C$2*($G$2-$B$2*B6-$D$2*D6),
(
)
1
3
x
=1/$D$3*($G$3-$B$3*B6-$C$3*C6),
( ) ( )
1 0
max
i i
i
x x
−
{=МАКС(ABS(B8:D8-B7:D7))}.
Фигурные скобки означают нажатие комбинации клавиш
CTRL+SHIFT+ENTER после набора формулы.
Остальные формулы для вычисления
(
)
k
i
x
получаются
копированием.
Можно провести вычисления в табличном процессоре Excel и с
использованием функций умножения матрицы на вектор на основе
матричной формы (2.9) метода Якоби.
Здесь
α=
−
−−
−−
02,03,0
2,006,0
25,05,00
, β=
4,0
1
25,1
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
