Руев Г.А. и др. Методы вычислений и их реализация в Excel
Подождите немного. Документ загружается.


91
( ) ( )
( )
( ) ( )
( ) ( ) ( ) ( ) ( )
( ) ( )
( ) ( ) ( )
( )
i
iiii
ii
iiiiii
ii
iihii
xu
h
h
uxu
h
xuhxu
xux
xu
h
xuhxuhxuxuu
h
uu
xuxuLxux
′′
=
−
′′
+
′
+
−
′
=
+
′′
+
′
+=+==
−
−
′
=−
′
=
++
++
2
2
...
2
,
2
2
11
1
δ
δ
Т.е. правая разностная производная имеет первый по
h
порядок
аппроксимации. Аналогичные оценки можно сделать для левой
разностной производной.
Центральная разностная производная имеет второй порядок
аппроксимации.
Аппроксимация второй производной по формуле (6.3) также
имеет второй порядок аппроксимации.
Для того чтобы аппроксимировать дифференциальное уравнение,
необходимо в нем заменить все производные их аппроксимациями.
Рассмотрим задачу (6.1), (6.2) и заменим в (6.1) производные:
( ) ( )
h
uu
xu
h
uuu
xu
ii
i
iii
i
2
,
2
11
2
11 −+−+
−
=
′
+−
=
′′
.
В результате получим:
ψϕ
==
−==−
−
+
+
−
−+−+
n
iii
ii
i
iii
uu
nizue
h
uu
q
h
uuu
,
,1,...,1,
2
2
0
11
2
11
(6.4)
Порядок аппроксимации исходной задачи равен 2, т.к. вторая и
первая производные аппроксимированы с порядком 2, а остальные –
точно.
Итак, вместо дифференциальных уравнений (6.1), (6.2) получена
система линейных уравнений вида
( )
( )
( )
ψ
ϕ
=
−=
=+++−−
=
+−
n
iiiiiii
u
ni
zhuhquehuhq
u
,1,...,1
,22242
2
1
2
1
0
(6.5)
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

92
для определения
i
u
в узлах сетки. Матрица данной системы имеет
вид:
( )
( )
( )
++−−
++−−
++−−
=
−−−
1...0000
2242000
..................
0022420
0002242
0...0001
11
2
1
22
2
2
11
2
1
hqehhq
hqehhq
hqehhq
A
nnn
Данная матрица является трехдиагональной, т.е. все ненулевые
элементы расположены на главной диагонали и двух прилегающих к
ней диагоналях.
Для решения таких СЛАУ имеется экономичный метод прогонки (см.
с. 31-32). Решая полученную систему уравнений, мы получим
решение исходной задачи.
Для краевой задачи (6.1), (6.2) имеем:
( )
( )
( )
ψ
ϕ
=
−=
=+++−−
=
+−
n
iiiiiii
u
ni
zhuhquehuhq
u
,1,...,1
,22242
2
1
2
1
0
Коэффициенты СЛАУ определяются формулами:
(
)
( )
.,1,0
,22,2,24
,1,...,2,2,2,24,2
1
11
2
1111
2
1
22
ψ
ϕ
=−==
−−=+=+=
−==+=+=−=
nn
iiiiiiii
fca
hqzhfhqbehc
nizhfhqbehchqa
Прямой этап метода прогонки:
ϕβα
==
11
,0
,
1
1
1
,
−
−
−
−
−
−=
−
=
iii
iii
i
iii
i
i
ac
af
ac
b
α
β
β
α
α
, i=2, 3, …n.
Обратный этап метода прогонки:
,0,...,2,1,
1
−−=+=
=
+
nniuu
u
iiii
n
βα
ψ
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

93
Условие устойчивости (условие диагонального преобладания) тогда
имеет вид:
hqhqeh
iii
−++≥+ 2224
2
.
Пусть
i
q
h
max
2
≤ .
Тогда
iii
hqqhqh ±=≥≥ max2
и, следовательно,
02
≥
−
i
hq
,
02
≥
+
i
hq
,
т.е.
42222 =−++=−++ hqhqhqhq
iiii
.
Тогда условие устойчивости имеет вид
424
2
≥+
i
eh
и, как можно
видеть, справедливо всегда.
ПРИМЕР 6.1.
Найти решение краевой задачи:
(
)
(
)
(
)
(
)
(
)
.11,00,4
=
=
=
−
′
+
′
′
uuxxuxuxu
Выпишем разностную схему
.1,0
,
2
4
2
0
11
2
11
==
=−
−
+
+
−
−+−+
n
ii
iiiii
uu
xu
h
uu
h
uuu
Условие устойчивости примет вид
5,0
4
2
max
2
==≤
i
q
h .
Пусть
2
,
0
=
h
.
Тогда число шагов
5
2,0
01
=
−
=n
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

94
.1
,2,0355115
,
21
1
221
,0
5
11
2
1
22
1
0
=
=+−
=
++
+−
−
=
+−
+−
u
iuuu
x
hh
u
h
u
hh
u
u
iii
iiii
Или
0
0
u
=
1 2
51 35 0,2
u u− + =
1 2 3
15 51 35 0,4
u u u− + =
2 3 4
15 51 35 0,6
u u u− + =
3 4 5
15 51 35 0,8
u u u− + =
5
1
u
=
Решим СЛАУ методом прогонки. Коэффициенты СЛАУ:
1,0,1
4,3,2,15
4,3,2,1,2,0,35,51,5
555
==−=
==
=====
fac
ia
iifbcn
i
iii
Прямой ход. Из первого уравнения находим:
51
2,0
51
35
21
−= uu
.
Сравнивая это выражение с основной формулой, видим, что
0039,0
51
2,0
,6863,0
51
35
11
−=−===
βα
.
Из второго уравнения
(
)
0113,0
5115
154,0
,8598,0
5115
35
5115
154,0
5115
35
4,0355115
1
1
2
1
2
1
1
1
3
2
32121
−=
−
−
==
−
−=
−
−
+
−
−=
=
+
−
+
α
β
β
α
α
α
β
α
β
α
u
u
uuu
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
95
Аналогично для третьего и четвертого уравнений:
(
)
0202,0
5115
156,0
,9186,0
5115
35
5115
156,0
5115
35
6,0355115
2
2
3
2
3
2
2
2
4
3
43232
−=
−
−
==
−
−=
−
−
+
−
−=
=
+
−
+
α
β
β
α
α
α
β
α
β
α
u
u
uuu
(
)
0296,0
5115
158,0
,9403,0
5115
35
5115
158,0
5115
35
8,0355115
3
3
4
3
4
3
3
3
5
4
54454
−=
−
−
==
−
−=
−
−
+
−
−=
=
+
−
+
α
β
β
α
α
α
β
α
β
α
u
u
uuu
Обратный ход начинаем с известного значения функции
1
5
=
u
Применяем прогоночное соотношение
9107,00296,019403,0
4544
=
−
⋅
=
+
=
β
α
uu
8164,00202,09107,09186,0
3433
=
−
⋅
=
+
=
β
α
uu
6907,0
2322
=
+
=
β
α
uu
4701,0
1211
=
+
=
β
α
uu
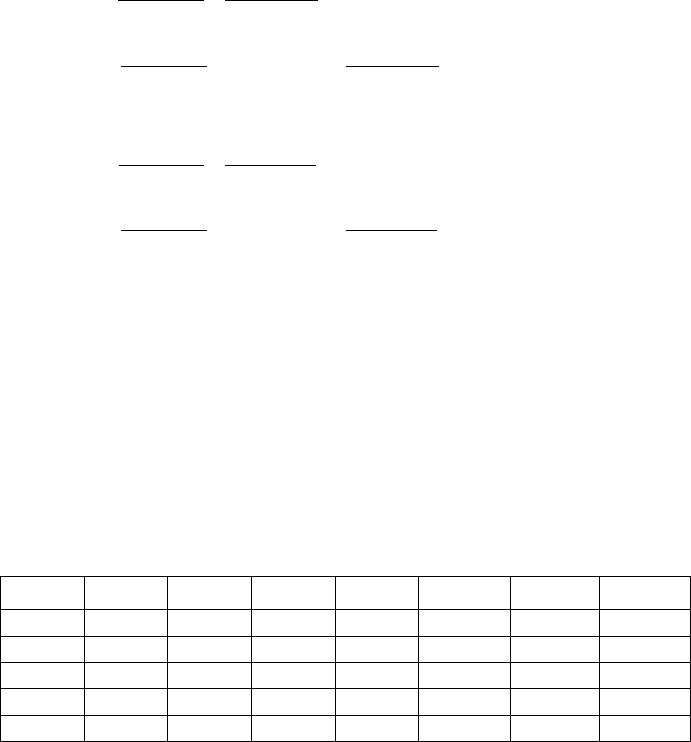
Вычисления оформим в виде таблицы:
i
i
a
i
c
i
b
i
f
i
α
i
β
i
u
1
51
35
0.2
0.6863
-0.0039
0.4701
2
15
51
35
0.4
0.8598
-0.0113
0.6907
3
15
51
35
0.6
0.9186
-0.0202
0.8164
4
15
51
35
0.8
0.9403
-0.0296
0.9107
5
0
-1
1
1
Рассмотрим задачу с граничные условия более общего вида.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

96
ПРИМЕР 6.2.
Решить ОДУ 2-го порядка
(
)
(
)
(
)
(
)
(
)
(
)
[
]
baxxzxuxexuxqxu ,,
∈
=
−
′
+
′
′
,
с краевыми условиями:
(
)
(
)
( ) ( )
0,,,,
,
,
222
111
>−
=
′
−
=
′
−
iiiii
const
bubu
auau
λγσλγ
σλγ
σλγ
В этом случае при построении разностной схемы необходимо еще
аппроксимировать и краевые условия. Аппроксимация в общем виде
выглядит так:
( ) ( )
h
uu
bu
h
uu
au
nn 101
,
−
−
≈
′
−
≈
′
.
В результате получим разностную схему:
1
01
101
σλγ
=
−
−
h
uu
u
1,...,2,
2
2
11
2
11
−==−
−
+
+−
−+−+
nizue
h
uu
q
h
uuu
iii
ii
i
iii
2
1
22
σλγ
=
−
−
−
h
uu
u
nn
n
Или
1
11
0
1
1
σ
λλ
γ
=−
−
h
u
u
h
(
)
(
)
(
)
1,...,2,22242
2
1
2
1
−==+++−−
+−
nizhuhquehuhq
iiiiiii
2
2
22
σ
λ
γλ
=
++−
n
n
u
hh
u
Мы получили СЛАУ типа (6.5) с трехдиагональной матрицей,
решение которой также можно найти методом прогонки.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
97
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
И РЕКОМЕНДАЦИИ К ЭКЗАМЕНУ
Задача 1.
Получить решение уравнения
(
)
099
23
=+−+= xxxxf
методом деления отрезка пополам с точностью 0,05.
Интервал изоляции
[
]
8,3;4
−
−
.
Проверим, что данных отрезок является интервалом изоляции
корня. Найдем значение функции на концах этого интервала:
(
)
34
−
=
−
f
,
(
)
768,28,3
=
−
f
. Т.е. на интервале содержится корень
уравнения. Проверим, что он единственный.
(
)
0923
2
=−+=
′
xxxf
097,2
6
93442
43,1
6
93442
2
1
−=
⋅⋅+−−
=
=
⋅⋅++−
=
x
x
Следовательно,
(
)
0
>
′
xf
на всем интервале
2
xx
<
, а
8,3097,2
2
−
>
−
=
x
,
т.е. функция
(
)
xf
монотонно возрастающая на
[
]
8,3;4
−
−
,
следовательно, данный интервал содержит один корень
уравнения и является интервалом изоляции.
Расчеты проведем в Excel по методу деления отрезка пополам,
результаты оформим в виде таблицы.
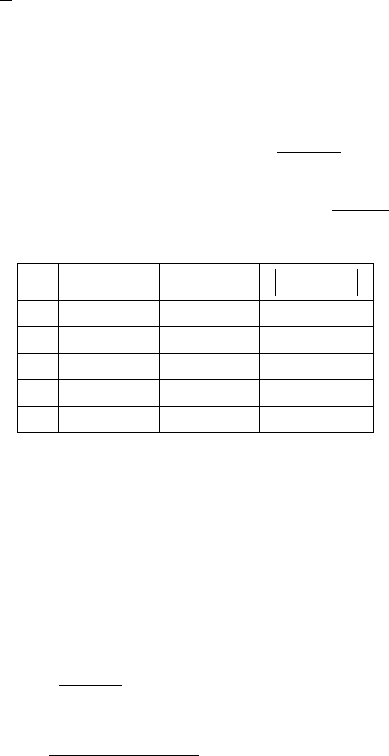
k
a
b
c
(
)
af
(
)
cf
ab −
0 -4
-3.8
-3.9
-3
-0.009
0.2
1 -3.9
-3.8
-3.85
-0.009
1.405875
0.1
2 -3.9
-3.85
-3.875
-0.009
0.705078
0.05
3 -3.9
-3.875
-3.8875
-0.009
0.349705
0.025
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

98
Расчетные формулы:
(
)
(
)
>⋅
=
−
−−−
случаепротивномвa
cfafеслиc
a
i
iii
i
,
;0,
1
111
(
)
(
)
>⋅
=
−
−−−
.,
;0,
1
111
случаепротивномвc
cfafеслиb
b
i
iii
i
,...2,1,0,
2
=
+
= i
ba
c
ii
i
Ответ: x=-3.8875
Задача 2.
Получить решение уравнения
(
)
099
23
=+−+= xxxxf
методом простой итерации с точностью 0.001. Интервал изоляции
[
]
3,5
−
−
.
Аналогично доказываем, что интервал является интервалом
изоляции.
(
)
465
−
=
−
f
,
(
)
183
=
−
f
(
)
0
>
′
xf
на всем интервале
2
xx
<
, а
3097,2
2
−
>
−
=
x
, т.е. функция
(
)
xf
монотонно возрастающая на
[
]
3,5
−
−
, следовательно, данный
интервал является интервалом изоляции.
Расчетные формулы:
(
)
kkk
xcfxx
−
=
+1
2
0
ba
x
+
=
[ ]
( )
[ ]
( )
xfmxfM
M
m
c
bax
bax
′
=
′
=
+
=
∈
∈
,
,
min,max,
2
Найдем значения констант. Для этого вычислим значения первой
и второй производных:
(
)
( )
026
923
2
=+=
′′
−+=
′
xxf
xxxf
.
Экстремум производной функции находится в точке
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
99
(
)
[ ]
3,5
3
1
0
−−∉−=
=
′
′
x
xf
.
Находим значения производной на концах отрезка
(
)
( )
1296273
56910755
=−−=−
′
=
−
−
=
−
′
f
f
.
Таким образом,
0294,0
56
12
2
,12,56 =
+
=== cmM
.
(
)
990294,0
23
1
+−+−=
+ kkkkk
xxxxx
,
4
2
35
0
−=
−
−
=x
.
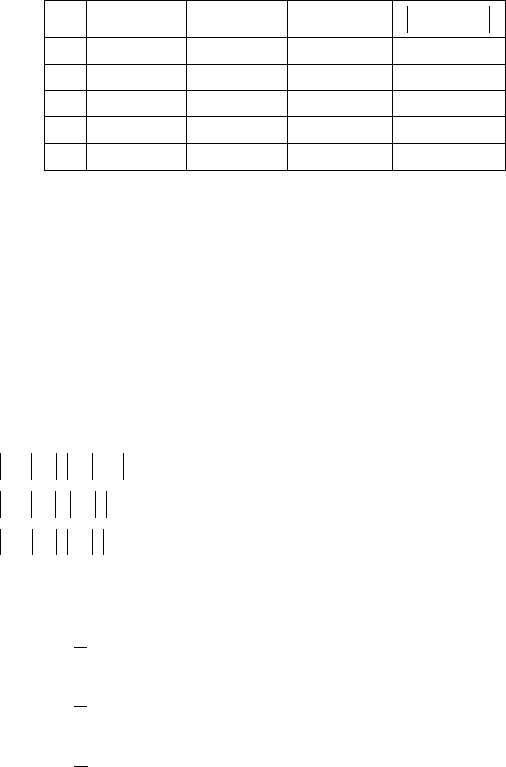
Вычисления оформляем в таблице
k
k
x
(
)
k
xf
1−
−
kk
xx
0
-4
-3
1
-3.9118
-0.35069
0.0882
2
-3.90149
-0.05198
0.01031
3
-3.89996
-0.0079
0.001528
4
-3.89973
-0.0012
0.000232
Ответ: x= -3,8997
Задача 3.
Получить решение уравнения
(
)
099
23
=+−+= xxxxf
методом Ньютона с точностью 0,001. Интервал изоляции
[
]
3,5
−
−
.
Проверка значений интервала изоляции была сделана в примере
выше. Расчетные формулы метода Ньютона:
(
)
( )
k
k
kk
xf
xf
xx
′
−=
+1
или в нашем случае
923
99
2
23
1
−+
+−+
−=
+
kk
kkk
kk
xx
xxx
xx
Выбираем нулевое приближение.
(
)
26
+
=
′
′
xxf
,
(
)
285
−
=
−
′
′
f
,
(
)
46945251255
−
=
+
+
+
−
=
−
f
. Знак функции и знак второй
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
100
производной совпадают на правом конце отрезка, поэтому выбираем
его в качестве начального приближения
5
0
−
=
x
.
Результаты представлены в таблице
k
k
x
(
)
k
xf
(
)
k
xf
′
1−
−
kk
xx
0
-5
-46
56
1
-4.17857
-8.89217
35.02423
0.821429
2
-3.92469
-0.72721
29.36009
0.253886
3
-3.89992
-0.00659
28.82821
0.024769
4
-3.89969
-5.6E-07
28.82332
0.000229
Ответ: x=-3,89969
Задача 4.
Решить систему линейных уравнений методом простой
итерации с точностью 0,05:
66
182
339
321
321
321
=−+
=+−
=−+−
xxx
xxx
xxx
Проверим условие диагонального преобладания:
2116
3128
4319
=+≥−
=+≥−
=−+≥−
Условия диагонального преобладания выполняются.
Разрешим систему уравнений относительно
i
x
( )
( )
( )
0
6
6
1
21
8
1
33
9
1
0
21
1
3
31
1
2
32
1
1
=
−−−=
−−−=
+−−=
+
+
+
i
kkk
kkk
kkk
x
xxx
xxx
xxx
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
