Руев Г.А. и др. Методы вычислений и их реализация в Excel
Подождите немного. Документ загружается.

21
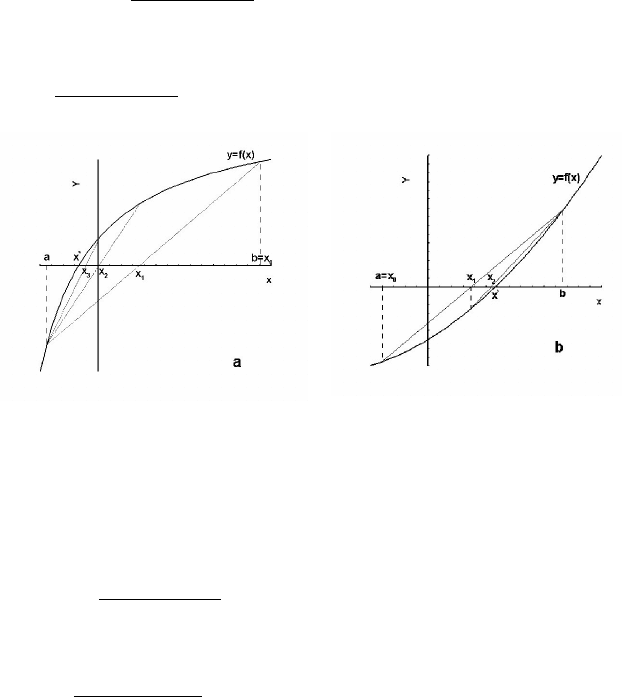
Следующее приближение
1
x
находим как точку пересечения
хорды, соединяющей точки
(
)
(
)
afa,
и
(
)
(
)
00
, xfx
с осью
x
.
Поскольку уравнение хорды записывается как
( )
(
)
(
)
( )
ax
ax
afxf
afy −
−
−
+=
0
0
,
то точка пересечения хорды с осью
x
находится из выражения:
(
)
(
)
( ) ( )
afxf
axaf
ax
−
−
−=
0
0
.
Рис. 1.6. Метод хорд для
(
)
(
)
0>
′
′
afaf
(a) и
(
)
(
)
0<
′
′
afaf
(b)
Пусть теперь
(
)
(
)
0<
′
′
afaf
(рис. 1.6, б).
Тогда
ax =
0
, точка
b
неподвижна.
Проведем хорду, соединяющую точки
(
)
(
)
bfb,
и
(
)
(
)
00
, xfx
:
( )
(
)
(
)
( )
0
0
0
0
xx
xb
xfbf
xfy −
−
−
+=
.
Вычисляем точку пересечения хорды с осью
x
:
(
)
(
)
( ) ( )
0
00
01
xfbf
xbxf
xx
−
−
−=
.
На следующей итерации в качестве
0
x
надо взять вычисленное
значение
1
x
и т.д.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

22
Таким образом, мы получим следующую последовательность
вычислений в зависимости от вида функции:
Если
(
)
(
)
0>
′
′
afaf
, то
bx =
0
и
(
)
(
)
( ) ( )
afxf
axaf
ax
k
k
k
−
−
−=
+1
.
Если же
(
)
(
)
0<
′
′
afaf
, то
ax =
0
и
(
)
(
)
( ) ( )
k
kk
kk
xfbf
xbxf
xx
−
−
−=
+1
, где
k
- номер итерации.
Окончание итерационного цикла в данном методе происходит
либо по условию малости невязки уравнения:
(
)
ε
<
k
xf
, либо по
условию
ε
<−
+ kk
xx
1
.
ПРИМЕР 1.5.
Найти первый и третий корень уравнения
01136
23
=++− xxx
методом хорд.
Концы интервала изоляции для первого корня
2
−
=
a
и
1
−
=
b
,
соответственно. Проверим знак выражения
(
)
(
)
afaf
′
′
для данного
уравнения:
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
0242712261123262
23
>−−=−−+−+−−−
.
Таким образом, расчет ведется по формулам:
bx =
0
и
(
)
(
)
( ) ( )
afxf
axaf
ax
k
k
k
−
−
−=
+1
.
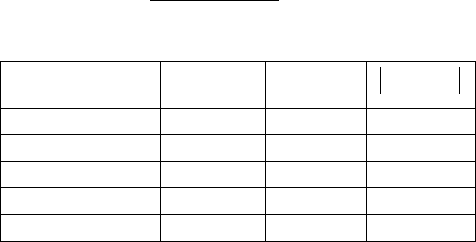
В результате получим таблицу:
Номер
итерации
k
x
(
)
k
xf
kk
xx −
+1
0 -1 1 -
1 -1.03571
0.345618
0.035714
2 -1.0479 0.117007
0.012187
3 -1.05201
0.039334
0.004108
4 -1.05339
0.013192
0.001379
5 -1.05385
0.004421
0.000462
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
23
Заданная точность достигнута на пятой итерации.
Для третьего корня
4
=
a
,
5
=
b
, и
(
)
(
)
(
)
(
)
01291246114346444
23
<⋅−=−⋅+⋅+⋅−=
′′
ff
,
следовательно, расчет ведется по вторым формулам:
ax =
0
и
(
)
(
)
( ) ( )
k
kk
kk
xfbf
xbxf
xx
−
−
−=
+1
.
Результаты вычислений показаны ниже:
Номер
итерации
k
x
(
)
k
xf
kk
xx −
+1
0 4 -9 -
1 4.9 -0.711 0.9
2 4.941555
-0.02147 0.041555
3 4.942783
-0.00062 0.001229
4 4.942819
-1.8E-05 3.57E-05
Заданная точность достигнута на четвертой итерации.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
24
МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
К решению систем линейных алгебраических уравнений сводятся
многочисленные практические задачи (по некоторым оценкам, более
75% всех задач). Можно с полным основанием утверждать, что
решение линейных систем является одной из самых
распространенных и важных задач вычислительной математики.
Существует много методов и современных пакетов прикладных
программ для решения СЛАУ, но для того, чтобы их успешно
использовать, необходимо разбираться в основах построения методов
и алгоритмов, иметь представления о недостатках и преимуществах
используемых методов.
Постановка задачи
Требуется найти решение системы
m
линейных уравнений,
которая в общем виде записывается в виде
=+++
=+++
=+++
mmmmmm
mm
mm
fxaxaxa
fxaxaxa
fxaxaxa
...
...
...
...
2211
22222121
11212111
. (2.1)
В матричном виде эта система уравнений записывается как:
fx
r
r
=A
(2.1′)
где
=
mmmm
m
m
aaa
aaa
aaa
...
............
...
...
21
22221
11211
A
- матрица системы,
=
m
f
f
f
f
...
2
1
r
- вектор правых частей,
=
m
x
x
x
x
...
2
1
r
- вектор неизвестных.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.

25
Таким образом, задача состоит в том, чтобы при известных
коэффициентах матрицы
A
и элементах вектора
f
r
найти такие
значения
(
)
T
m
xxx ...
21
, что при подстановке их в систему
уравнений (2.1) они превращаются в тождества.
Необходимым и достаточным условием существования
единственного решения СЛАУ является условие
0det
≠
A
, т.е.
определитель матрицы
A
не равен нулю. В случае равенства нулю
определителя матрица
A
называется вырожденной и при этом СЛАУ
(2.1) либо не имеет решения, либо имеет их бесчисленное множество.
В дальнейшем мы будем предполагать наличие единственного
решения.
Все методы решения линейных алгебраических задач можно
разбить на два класса: прямые (точные) и итерационные
(приближенные).
Прямые методы решения СЛАУ
Метод Крамера
Метод Крамера относится к классу точных методов решения
СЛАУ. На практике он часто используется при небольшой
размерности системы
52
÷
=
m
. Формулы метода Крамера решения
СЛАУ выглядят как:
A
A
det
det
i
i
x =
, (
m
i
,...,
2
,
1
=
) (2.2)
Эти формулы позволяют находить неизвестные в виде дробей,
знаменателем которых является определитель матрицы системы, а
числителем – определители матриц
i
A
, получаемых из
A
заменой i-
го столбца столбцом правых частей. Так матрица
1
A
получается из
матрицы
A
заменой первого столбца на столбец правых частей
f
r
.
Размерность системы (т.е. число неизвестных
m
) является
главным фактором, из-за которого формулы Крамера не могут быть
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
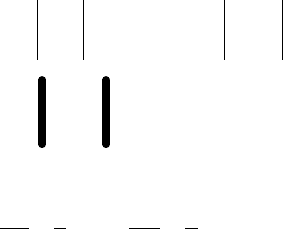
26
использованы для численного решения СЛАУ большого порядка. При
непосредственном раскрытии определителей решение системы с
m
неизвестными требует порядка
m
m!
арифметических операций.
Таким образом, для решения системы, например, из
100
=
m
уравнений потребуется совершить
158
10≈
операций, что не под силу
даже самым мощным современным ЭВМ. Для небольших m решение
можно найти с помощью функций Excel.
ПРИМЕР 2.1.
Рассмотрим метод Крамера на примере системы двух линейных
уравнений вида
=−
=+
02
1
21
21
xx
xx
.
Найдем определители:
1
02
11
det
1
−==A
,
2
10
11
det
2
−=
−
=A
,
3
12
11
det
1
−=
−
=A
.
Решение по формулам Крамера:
3
1
3
1
1
=
−
−
=x
,
3
2
3
2
2
=
−
−
=x
.
ПРИМЕР 2.2.
Решить методом Крамера СЛАУ
=++
=++
−=+
5853
723
12
321
321
21
xxx
xxx
xx
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
27
Занесем на рабочий лист матрицу СЛАУ, вектор правых частей
f
,
A=
853
231
012
, f=
5
7
1−
, а также вспомогательные матрицы
A
1
=
−
855
237
011
A
2
=
−
853
271
012
A
3
=
−
553
731
112
.
С помощью функции Excel МОПРЕД вычислим
∆ = det A = 26,
∆1 = det A1 = - 60,
∆2 = det A2 = 94,
∆3 = det A3 = - 20.
По формулам (2.2) находим
x1 = ∆1/∆ = - 2.3077,
x2 = ∆2/∆ = 3.6154,
x3 = ∆3/∆ = - 0.7692.
Метод обратной матрицы
Если
0det
≠
A
, то существует матрица
1−
A
, обратная к данной.
Умножим исходную систему уравнений (2.1) на обратную матрицу
слева. Получим
fx
r
r
11 −−
= AAA
.
Известно, что произведение обратной матрицы на исходную дает
единичную матрицу
E
, и, следовательно, получаем
fx
r
r
1−
= AE
, или
fx
r
r
1−
= A
(2.3)
Решение СЛАУ свелось к умножению известной обратной
матрицы на вектор правых частей. Таким образом, задача решения
СЛАУ и задача нахождения обратной матрицы связаны между собой,
поэтому часто решение СЛАУ называют задачей обращения матрицы.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
28
Проблемы использования этого метода те же, что и при
использовании метода Крамера: нахождение обратной матрицы –
трудоемкая операция. Однако для небольших m решение может быть
получено с помощью функций Excel.
ПРИМЕР 2.3.
С помощью метода обратной матрицы решить систему
=+−
=++
=++
41023
553
10248
321
321
321
xxx
xxx
xxx
Занесем на рабочий лист Excel матрицу коэффициентов
−
=
1023
153
248
A
и вектор правых частей
=
4
5
10
f
r
.
Выделим на рабочем листе область размером
33
×
ячейки для
обратной матрицы и вызовем функцию МОБР.
В поле Массив занесем адреса ячеек исходной матрицы A, и, нажав
комбинацию клавиш Ctrl+Shift+Enter, получим A
-1
:
0.195489
-0.16541
-0.02256
-0.1015
0.278195
-0.00752
-0.07895
0.105263
0.105263
Полученную обратную матрицу умножим на вектор правых частей
f
r
.
Для этого выделим столбец из трех ячеек и вызовем функцию
МУМНОЖ.
В поля Массив 1 и Массив 2 занесем адреса ячеек, в которых
находятся найденная обратная матрица и вектор правых частей, после
чего, нажав комбинацию клавиш Ctrl+Shift+Enter, получим решение
СЛАУ
1.037594
0.345865
0.157895
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
29
Замечание.
Если одна из клавиш Ctrl или Shift не нажата, вычисления будут
выполнены не во всем выделенном диапазоне, а только в одной
ячейке. В этом случае весь процесс вызова функции необходимо
повторить.
Метод Гаусса
Наиболее известным и популярным прямым методом решения
СЛАУ является метод Гаусса. Этот метод заключается в
последовательном исключении неизвестных. Метод состоит из двух
этапов.
На первом (прямом) этапе исходная система сводится к системе с
треугольной матрицей, которая решается на втором (обратном) этапе.
На прямом этапе используются следующие эквивалентные
преобразования строк расширенной матрицы системы: перестановка
строк, умножение строки на ненулевую константу, сложение строк.
Прямой этап. Пусть в системе уравнений
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
=+++
=+++
=+++
00
2
0
21
0
1
0
2
0
22
0
221
0
21
0
1
0
12
0
121
0
11
...
...
...
...
mmmmmm
mm
mm
fxaxaxa
fxaxaxa
fxaxaxa
первый элемент
(
)
0
0
11
≠a
.
Назовем его ведущим элементом первой строки.
Разделим все элементы этой строки на
(
)
0
11
a
, и исключим
1
x
из всех
последующих строк, начиная со второй, путем вычитания первой
(преобразованной), умноженной на коэффициент при
1
x
в
соответствующей строке. Получим
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
=++
=++
=+++
11
2
1
2
1
2
1
22
1
22
1
1
1
12
1
121
...
...
...
...
mmmmm
mm
mm
fxaxa
fxaxa
fxaxax
.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
30
Если
(
)
0
1
22
≠a
, то на него можно разделить второе уравнение, а
затем исключить
2
x
из всех остальных уравнений.
С помощью аналогичных преобразований приходим к системе
уравнений с верхней треугольной матрицей
( ) ( ) ( ) ( )
( ) ( ) ( )
( ) ( )
( )
=
=++
=+++
=++++
m
mm
mm
mm
mm
fx
fxax
fxaxax
fxaxaxax
...
...
...
...
3
2
3
23
2
2
2
23
2
232
1
1
1
13
1
132
1
121
(2.4)
Обратный этап.
Решаем систему (2.4) с верхней треугольной матрицей в обратном
порядке:
( )
( ) ( )
( ) ( ) ( ) ( )
−−−−=
−=
=
−
−
−
−−
mm
m
m
mm
m
mm
m
mm
xaxaxafx
xafx
fx
1
13
1
132
1
12
1
11
1
,1
1
11
...
...
. (2.5)
В случае если один из ведущих элементов равен нулю,
изложенный алгоритм метода Гаусса неприменим. Кроме того, если
какие-либо ведущие элементы малы, то это приводит к усилению
ошибок округления и ухудшению точности счета.
Поэтому обычно используется другой вариант метода Гаусса –
схема Гаусса с выбором главного элемента.
Путем перестановки строк и других эквивалентных
преобразований добиваются выполнения условия:
(
)
(
)
,
00
ijii
aa ≥
miiij ,...,2,1,1,...,1
+
+
−
=
,
т.е. осуществляется выбор первого главного элемента.
Переставляют уравнения так, чтобы в первом уравнении
коэффициент
11
a
был максимальный по модулю.
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
