Розенберг В.Я. Введение в теорию точности измерительных систем

Подождите немного. Документ загружается.

согласно определению, приведенному в § 1.4, следует, что в схеме изме-

рения (см. рис. 1.3,а и 1.6) отсутствуют какие бы то ни было вероят-

ностные механизмы, оказывающие возмущающие воздействия, за исклю-

чением основного вероятностного механизма ВМ

, определяющего смысл

измерительного эксперимента, ввиду чего идеальная система является

детерминированной. Это предположение, в частности, означает отсут-

ствие ограничений на объем наблюдений, обусловливаемых действием

ВМ~; наблюдению оказывается доступным весь ансамбль реализаций

случайного процесса, т. е. сам процесс, а не конечный набор его реали-

заций. Из этого же предположения вытекает, что тезаурус считается

полным, т. е. содержащим модели, адекватно описывающие исследуе-

мые объекты. Далее, предположение о комплексном характере измере-

ния (см. § 1.4) означает, что определяется вид математической модели

и значения ее параметров; что касается оценки степени адекватности мо-

дели, то необходимость в такой оценке отпадает в силу предположения

о полноте тезауруса.

С учетом сказанного, перепишем выражение (2.85) в виде

{(х, у)

у=А

х; х, уеЕМ}, (3.1)

где х отождествляется с исследуемым объектом (процесс, система); у—

результат измерения, — модель объекта х; А

— оператор ИС, закон, по

которому любому объекту х ставится в однозначное соответствие его

модель у; М — тезаурус, используемый при измерении.

Допустим, что тезаурус задан в виде (2.5), т. е.

М = {т-.т=П{х, а.г), 1е={ТД}, (3.2)

Задача измерения состоит в следующем: предъявлен объект х,

«истинная» модель которого т

, априори неизвестная, принадлежит те-

заурусу М:

х = т

= ]{Х)А{1

Х, а/) (3.3)

Необходимо найти оператор (закон, правило, алгоритм) А

, кото-

рый каждому т

ставит в соответствие его модель

у=т*

=!}

(х, а,и)е1. (3.4)

Способ нахождения этого оператора, который можно назвать «син-

тезом по определению», состоит в следующем. Допустим, что на множе-

стве М задано расстояние р (1.26), т. е. (М, р) —метрическое простран-

ство. Условие т

, т

^М означает, что

Уг> а/Нэ'и, : / (л:) =

(л,а,

), (3-5)

откуда

Г(х)-Мх, а*)=-0 (3.6)

и, на основании (1.26),

иА*> а/„) = аг^ттр[7(х), ^(х, а/)] =

= аг§р[7(х), //и (х, а/и)], (3.7)

где

р[Г(х), а,)] =

р(|Г(х)-№х,

а,)|).

Выражение (3.7), которое в иных обозначениях можно переписать

в виде

т*

= аг^1шпр(л:, т

), (3.8)

уе

совпадающем с (1.31), представляет собой искомый алгоритм измере-

ния. Из аксиомы тождества (1.26) и (3.5) следует, что для идеальной

системы

гат

[7(х), !,-(х, а/)] = 0 (3.9)

/, а/

и /и = «, а

/н

а,-

для любого функционала, удовлетворяющего (1.26).

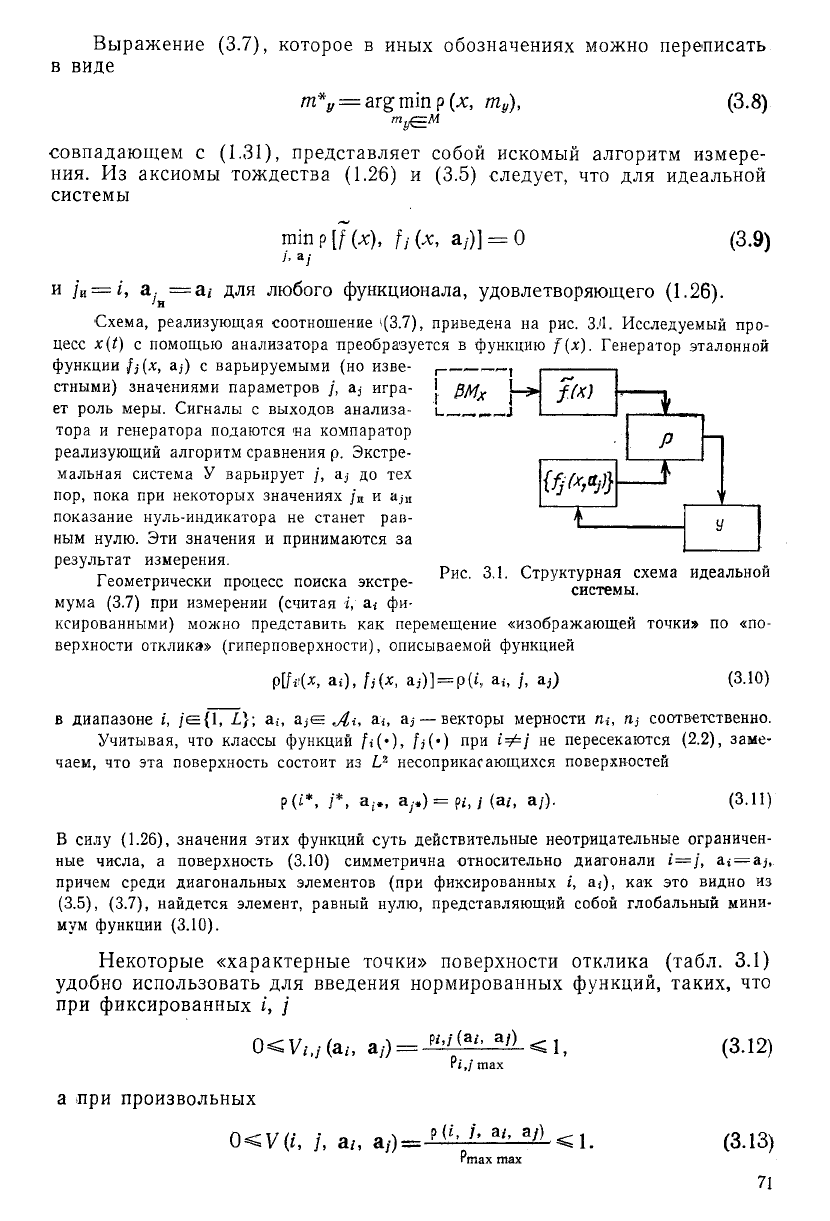
•Схема, реализующая соотношение <(3.7), приведена на рис. ЗЛ. Исследуемый про-

цесс х(() с помощью анализатора преобразуется в функцию [(х). Генератор эталонной

функции }}(х, а,) с варьируемыми (но изве-

стными) значениями параметров /, а,- игра-

ет роль меры. Сигналы с выходов анализа-

тора и генератора подаются «а компаратор

реализующий алгоритм сравнения р. Экстре-

мальная система У варьирует /, а,- до тех

пор, пока при некоторых значениях /

и а^и

показание нуль-индикатора не станет рав-

ным нулю. Эти значения и принимаются за

результат измерения.

Геометрически процесс поиска экстре-

мума (3.7) при измерении (считая I, а,- фи-

ксированными) можно представить как перемещение «изображающей точки» по «по-

верхности отклика» (гиперповерхности), описываемой функцией

аО, [](х, а,)] = р(г, а

(

, а,) (3.10)

в диапазоне I, /е{1, I}; а;, а^е а;, а,- — векторы мерности Пг, п, соответственно.

Учитывая, что классы функций /г('). Ы')

И не

пересекаются (2.2), заме-

чаем, что эта поверхность состоит из I? несоприкасающихся поверхностей

(I*, /*, а;., а

.) =

р«,

/ (а/, а/). (3.11)

В силу (1.26), значения этих функций суть действительные неотрицательные ограничен-

ные числа, а поверхность (3.10) симметрична относительно диагонали »=/, аг = а,-,

причем среди диагональных элементов (при фиксированных I, а,-), как это видно из

(3.5), (3.7), найдется элемент, равный нулю, представляющий собой глобальный мини-

мум функции (3.10).

Некоторые «характерные точки» поверхности отклика (табл. 3.1)

удобно использовать для введения нормированных функций, таких, что

при фиксированных /

0<У,.

(а,, а/) = "'

(а/

а/)

<1, (3.12)

1,1 шах

а при произвольных

0<У(г, /, а/, а,)=

р(

'' ''

а/

а/)

<1. (3.13)

Ртах тах

Рис. 3.1. Структурная схема идеальной

системы.

Таблица 3.1

Наименования характерных точек и значений

Характерные точки и значения поверхности отклика

Координаты минимумов:

локальных (г ф /)

глобального (г = /)

(а*1, а*/)

—

аг§ тт

(г*, /*, а

;

», а -,)

аге.^г

а/е^у

Значения, локальных минимумов

р(а*/, а*/), г*, /* = Т71

(

(а*1, а*/) = 0,

Наибольшее расстояние между

элементами класса

5црр(/*, /*, а,.., а у») =Р;

/Шах

, /*=Т1

а^еМ

а у.е^/

Наибольшее расстояние между

элементами тезауруса

зирр (г, /, аи а/) = р

тахтах

а/е^/

Результат измерения также соответствует максимуму функций

0<Л

4>3

-(а«, а,) = 1-1/^-(аг, (3.14)

0<Л(1, /, а,) = 1—У{1, /, а

)<1, (3.15)

так как монотонное преобразование не смещает точки экстремума.

Свойства функций (3.12) — (3.15) и, в частности, элементы, обра-

щающие неравенства в равенства, с учетом свойств функции (3.10) и

табл. 3.1—очевидны.

Важный смысл приобретают экстремальные значения

= (3.16)

1/**,.=р*/р

тахтах

(3.17)

•функций (3.12) и (3.13) соответственно, сравниваемые между собой для

всех г, /' в процессе поиска глобального экстремума в (3.7).

Пример 1. Критерии метрического пространства. Рассмотрим (3.16)

з случае, когда М представляет собой функциональное метрическое пространство I

-{1.30). Имеем

и) = \\п-и\к

={1\п(х)-п(х)\рс1ху

1р

, (зле)

—00

где |[-||—знак нормы [72]*).

Используя неравенство Минковского [72], можем записать:

Р01

(Ь-Ь) = II/оь II 11^11^=2, (3.19)

*> Для упрощения письма во всех последующих выражениях, содержащих опре-

деленные интегралы, обозначения пределов (областей) интегрирования опускаем, за

исключением случаев, требующих особого указания.

где и = }/\\} Ц^ — нормированные функции; или

откуда получаем нормированные функции р

0Л

^ и р^ соответственно в виде

Ч = "2"

II — /о

или

п -

ь.

V, =1

111„

1ь,

4-{ ]

|Ы*)-М*)1"'**

{{|Л (х)-и(х) \рл%у

,р

1/р

а в соответствии с (3.14), (3.15)

МР

Лоь

= 1—Уоь,

Лх.

= 1—Уь.

(3.20).

(3.21У

(3.22>

(3.23>

Формула (3.21), при значениях р=1, р=2, р = оо, в условиях наилучшего при-

ближения функций ?\{х) и /

(х, а) имеет вид, указанный в табл. 3.2. Заметим, что.

Таблица 3.2\"

Р^п

Ш1П

Г(*) -

? {X,

а) | =

шш

]/1 [Г(*)-И*. а)]

тттах| / (х)

—

(х, а) | =

а х

[Цх)-Т(х< а*)]

йх

V]Р (*) + У1

(х, а*) йх

\!(х*)-!(х*,а*)[

Г(

/ (•**•

*) |

частным случаем (3.20), когда ^(х) и Ь(х) суть плотности вероятности и р— 1»,

является так называемое расстояние по вариации

причем, очевидно,

Л^ =

1 —

= ^ (тт) [/>, (х),

р*

(х)] йх,

(3.24>

где (гаш)(',') означает, что интегрирование производится по той из функций, кото-

рая при данном х имеет меньшее значение.

Заметим, что функционалы (3.12) — (3.15) не удовлетворяют аксиоме треугольни-

ка, а (3.14), (3.15)—также и аксиоме тождества, т. е. они не являются расстоянием

(1.30). Очевидно, однако, что их свойства таковы, что позволяют с успехом исполь-

зовать их для решения задачи измерения. Приведем еще два примера подобных функ-

ционалов, применение которых оказывается эффективным при сравнении функций опре-

деленных классов [11, 95].

Пример 2. Корреляционный критерий имеет вид

рх=\1ШЫх)ах\

и существует для

}(х)1=Ь

Из неравенства Буняковского-Шварца следует

11 (хО Ы(х)йх |

= , /~р

=| ГМ*)М*)Л*| <1. <

у 5/м*)

Лс

) №)<**

и 1

Равенство слева достигается в случае, когда сравниваемые функции ортогональ-

ны, справа — когда ^(х) = а?

(х); (а = сопз{). Как обычно,

= 1—А

. (3.26)

Легко показать, что связано с У

ц соотношением

В условиях наилучшего приближения

| (х) ! (х, а) йх |

У*^ =

— тах

у^ |

(х) йх | р (х, а) йх

\Г(х)!(х, а*)йх\

= 1 •'

-, (3.27)

у (х, а*)йх

где а* — результат измерения.

Пример 3. Энтропийный критерий [95].

Пусть

{Цх)} = {1(х):}(х)еи, || Ц») ||^=1, ?(х)>0}. (3.28)

Поскольку этому условию удовлетворяет, например, множество одномерных плотностей

вероятностей, далее для конкретности будем иметь в виду именно эти функции и обо-

значим {((х)} Д {р

(х)}

Д с/-.

Необходимо определить критерий сравнения функций Р\(х),

(х)<^3>

удовле-

творяющий условиям 0^р(рь р

)<°° и р(р

рг) = 0 <==>

р1

= рг.

Предварительно рассмотрим вспомогательное утверждение. Пусть, дополнительно

к (3.28), 3* удовлетворяет некоторым довольно общим ограничениям вида

3» = {р(х) :Л(Р)= /

Яг(х)р(х)йх=Сг-,

»=1ТТ}, (3.29)

где (Л:) — некоторые функции; с

— константы.

Определим также функционал

Я(р)=—

р(х)\п р(х)йх, (3.30)

называемый энтропией. В [38] приведены примеры решения «прямой» задачи: в усло-

виях (3.28), (3.29) найти так называемое экстремальное распределение р{х), достав-

ляющее максимум энтропии (3.30).

Нам необходимо решение «обратной» задачи, формулируемой следующим обра-

зом: дано некоторое конкретное распределение р(х); требуется найти минимальные

(к=

ограничения вида (3.29), при которых р(х)—р(х). Решение этой вариационной

задачи имеет вид [97]

Н (р) = — | р (X) 1п"р (х) ах Д М {— \ър (х)}. (3.31)

Например, полагая

1 - —

Р №

= е

2по

учитывая, что

| р (х) ёх = 1, Н (р) = — 1п

—00

иа основании (3.31) получаем (3.29) в виде '>

3» = |р(х) :Р(р) = ^ х*р(х)йх =

о*

еп ерь , имея в виду, что р1 (х) = р (х) можем записать

А Н(ри Рг) ДЯМ-Я

(Рг)

ДН(р

рг) = Н (

Р1

) - Н (р

(3.32)

что находится в полном согласии с условиями, указанными в иостановке задачи.

Величину (3.32) можно пронормировать, используя, например, следующие вы-

ражения

= кН/Н (рг),

А<1

= 1—Уа,

= е~

ля

, (3.33)

У я = 1—Лн, (3.34)

где Ул — относительная энтропия; Л^ — избыточность [38]; А

— энтропийный коэф-

фициент подобия; Ун—энтропийный коэффициент различия [95] сравниваемых рас-

пределений.

Отметим некоторые свойства коэффициента А

1) для «абсолютно неслучайной», т. е. детерминированной величины рг(х) =

=6(х) (6(х) — дельта-функция Дирака).

В этом случае

//,ДЯ (р

) = — | 3 (х) 1п 8 (х) ах = — оо

и поэтому

= е

Нз

/е

Н1

= 0;

2) если распределение рг(х) экстремально, т. е. р

(х)=р(х)=р\(х), АН—0 и

Лн=е°=.'1.

Таким образом О^Ан^.! и Лн возрастает по мере увеличения степени неопреде-

ленности р

(х) в пределах наложенных на него ограничений. Примеры применения

указанных критериев в ряде измерительных задач содержатся в [11]. Некоторые из та-

ких примеров будут приведены ниже.

Свойства поверхности неопределенности представляют интерес

с точки зрения выбора эффективных алгоритмов поиска экстремума.

Например, для поверхностей (3.11), расположенных на диагонали I*

—

=/*, следует считать, что функции }г(х, а,), ^{х, а,) принадлежат одно-

му и тому же параметрическому семейству {/(х, а)}, причем вид функ-

ции / известен. Таким образом,

^(х, а*) А/(х, а*) Ау и

//(*. а/)Д/(*, а/) 4 у,-.

Поскольку р есть метрика, вследствие аксиомы симметрии имеем

р(а», а

;

)=р[/(х, а,-), Цх,

-)]

;

[/(х,

), }(х, а

)] = р(а

, а*), (3.35)

•т. е. функция р(а,-, а

) симметрична относительно своих аргументов.

Без введения уточняющих предположений трудно высказать какие-либо

дополнительные соображения относительно свойств поверхности (3.11).

Необходимо выбрать вид функций а,) и функционала р.

Пример {101]. Рассмотрим свойства функции (3.35) применительно к одному до-

статочно представительному классу функций, определяемому выражением

У = |/(х, а, Ь, с): I (х, а, Ь,

с)

—а\

Для пространства Ьр (1.30) можем переписать (3.18) в виде

{<Н,

Ы, С1, а/, 6/, с/) = |

сражение привод!

йх

ИР

После несложных преобразований это выражение приводится к виду

р )ЧР

йх

, (3.36)

рМк

где а=а

7а

(

<=(—оо, оо), оо, оо); т== (с

— с^/^-е (—оо, оо).

Параметры а,-, 6,- считаются фиксированными. Отрица-

тельным значениям Р соответствует изменение направления оси

аргумента с надлежащим изменением масштаба.

Исследование поверхности р(а, т) проведем, рассма-

тривая ее сечения плоскостями, проходящими через точку экс-

тремума (а=1, Р=1, т=0). Нас будет, в частности, интере-

совать «острота» этой поверхности вблизи точки экстремума,

определяющая разрешающую способность измерения параме-

тров а.1, Ьи с,. (Напомним, что в радиолокационных задачах

разрешающая способность определяется аналогичными свой-

ствами «функции неопределенности» [41].)

1. Функция

О 1

Рис. 3.2. Сечение по-

верхности отклика

плоскостью (аОр).

РИДРК I. 0) = | а I | {^(х)|РЛс}

,/р

(3.37)

представлена на рис. 3.2. Угловой коэффициент определяется выражением

аф\

1р

С |

! (х) \Рйх^'

(а - 1).

Существенно следующее:

— зависимость р(а) линейна по обе стороны от точки экстремума и, как следо-

вало ожидать, симметрична относительно оси а=1;

до (а)

Ъг—ъг

— разрешающая способность, определяемая значением первой производной по па-

раметру в точке экстремума, тем больше, чем больше норма импульса и пропорцио-

нальна а, и й,:'/з>;

— разрешающая способность не зависит от формы [(х) импульса.

2. Рассмотрим поведение функции

р (Р)

(1. Р. 0) = афур {|

!(х)~! (Х/Р) \ра

1р

Применяя неравенство Минковского, имеем

Р (Р)

афУР [

{11 !(х)

Iрах)

11р

+ {|1! (х/Р)!РОх]

1/р

] =

= аф\1Р(

+ р'

/Р

) {{|Г(х)|рах}

1/р

. (3.38)

В частном случае при 1 для функций, монотонно убывающих по обе стороны от

единственного экстремума,

откуда

р,(Р)=а,6

(Р-1) / \Н*)№,

что аналогично (3.37) (рис. 3.3). На графике

<*Р1

(Р)

•

ар

аф1 \ | / (х) |

д,х

51§п (р-1).

Заметим, что измерение |3 можно уподобить измере-

нию скорости подвижной цели в импульсной радиолокации.

Если расстояние до цели Ж^)=V^, то запаздывание им-

пульса

т(0=2ш7с=рЧ.

Задержанный импульс

Г (() = {[(=110 -Р'Н], т. е. р:

\ 1 /

Рис. 3.3. Сечение поверх-

ности отклика пло-

скостью (|30рх).

— р' 1 —

20/с

ИР

или

= (Р'

— 1) с/2р.

3. Рассмотрим теперь функцию

РМД Р(1, 1,

= аф\

Р /(*)-/(х-г)|РЙх}'

Отметим следующее:

а) РМ=РН).

Действительно,

Р (т)

{

(х) —/(х—т) | Рйх] Ч>

= { Л / (х+т) -I

(х) |

йх} ЧР = р

(—т),

что, впрочем, видно и из (3.35);

(3.39)

б) 11т р(х) = / [ |^(х)|Рйх)

1/р

= тахр(1:)

1 |-»00 I ^

> 1

+ {/ |/(х—Т)|РЙХ}

/Р = 2{/ \!(х)\рахуп>.

Если рассмотреть функцию (3.14), в данном случае имеющую вид

рМ

Л(т) = 1

тах

(т) '

то, как легко видеть, действительно 0<А(:)<А(")=1 и, кроме того, Нгп Л(т)=0-

I т |->00

Далее, функциям /(*), отличным от нуля в конечном интервале Д, соответствует

функция Л(т), отличная от нуля в интервале 2А. Если же область существования

}(х) ограничена лишь с одной стороны или вообще не ограничена, то область сущест-

вования Л(т) не ограничена с обеих сторон. Отмеченные свойства функции Л(т) ана-

логичны свойствам нормированной функции корреляции (3.25)

Г/(х)Г(х-х )йх

. (3.40)

Ар М

| (х) йх

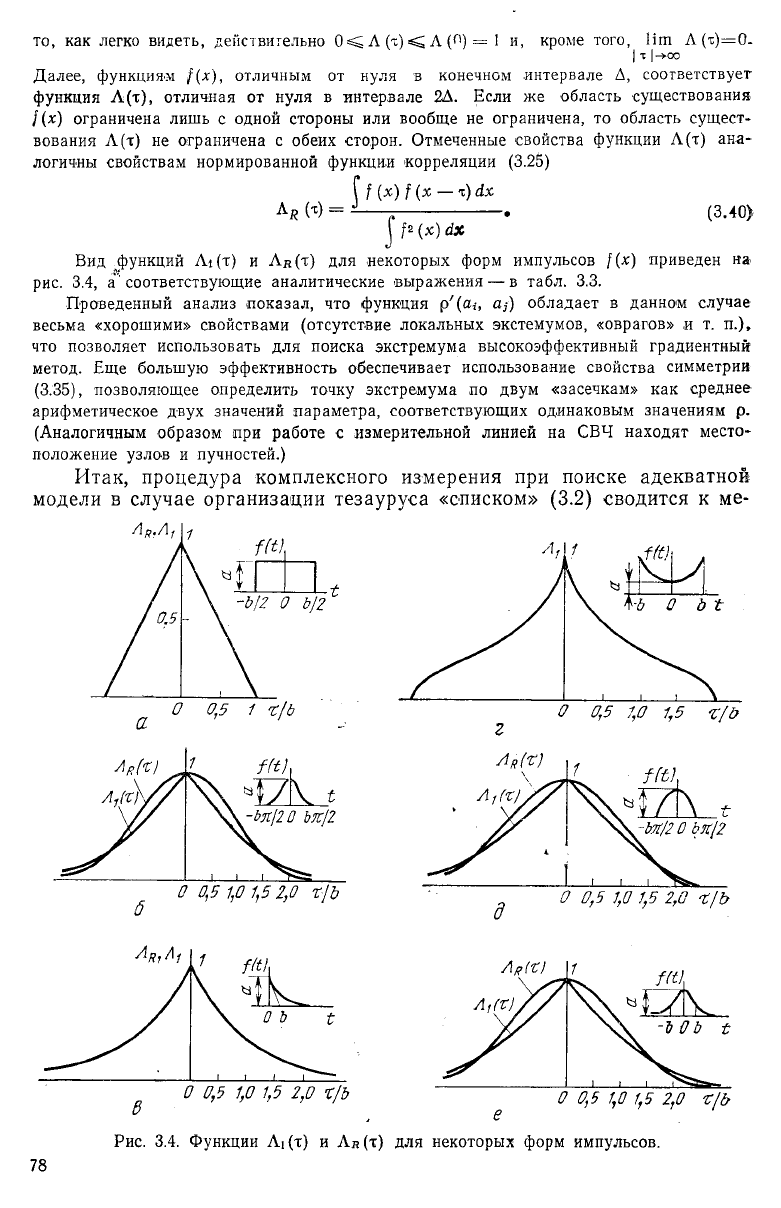
Вид функций

Д.1

(т) и Л

(т) для некоторых форм импульсов }{х) приведен на

рис. 3.4, а' соответствующие аналитические выражения — в табл. 3.3.

Проведенный анализ показал, что функция р'(а,, а,-) обладает в данном случае

весьма «хорошими» свойствами (отсутствие локальных экстемумов, «оврагов» и т. п.),

что позволяет использовать для поиска экстремума высокоэффективный градиентный

метод. Еще большую эффективность обеспечивает использование свойства симметрии

(3.35), позволяющее определить точку экстремума по двум «засечкам» как среднее

арифметическое двух значений параметра, соответствующих одинаковым значениям р.

(Аналогичным образом при работе с измерительной линией на СВЧ находят место-

положение узлов и пучностей.)

Итак, процедура комплексного измерения при поиске адекватной

модели в случае организации тезауруса «списком» (3.2) сводится к ме-

О 0,5 1 х/Ь

-Ьж/20 ЬХ/2

О 0,5 1,0 1,5 2,0 Г]Ь

О 0,5 1,0 1,5 2,0 Х/Ь

ьоь г

О 0,5 1,0 1,5 2,0 Г/^

Рис. 3.4. Функции Л[ (т) и Лл(т) для некоторых форм импульсов.

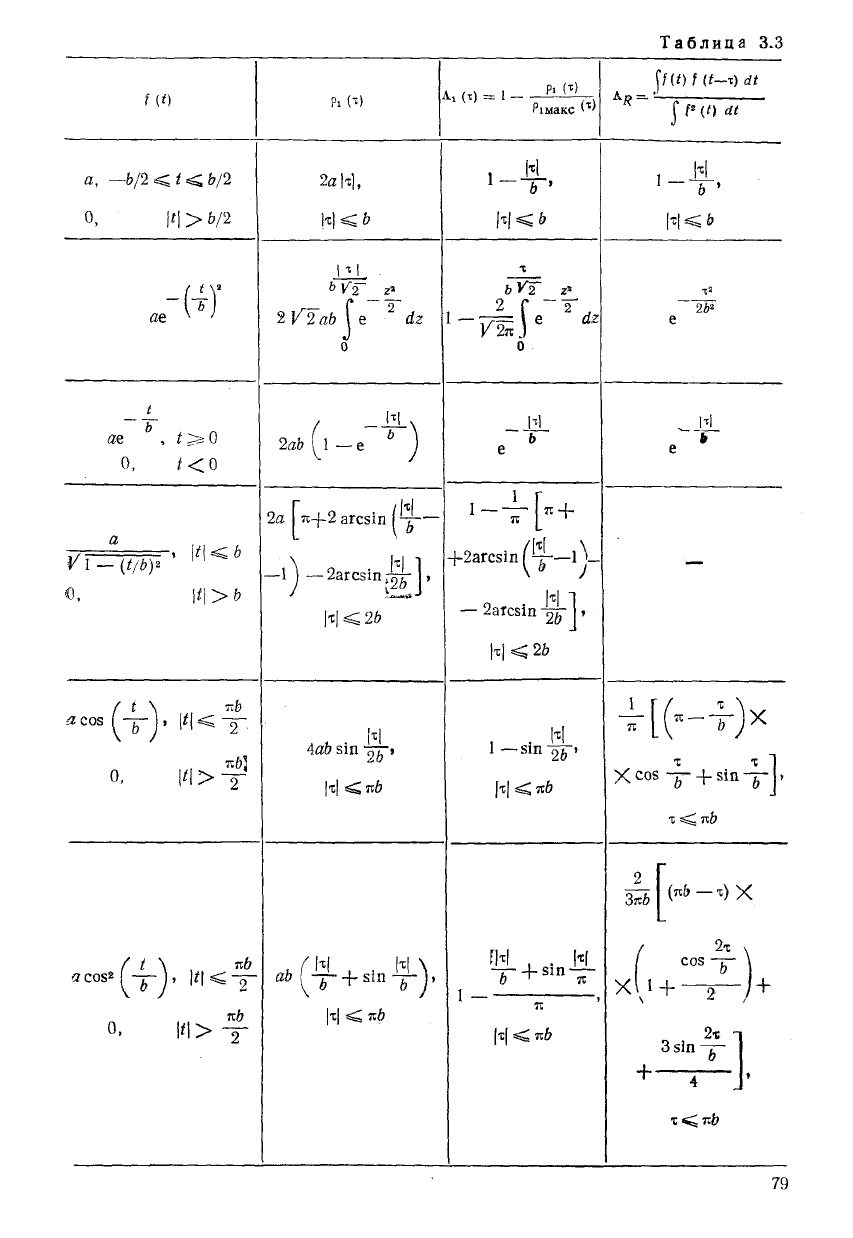
Таблица 3.3

ПО

Р1

Ршакс <

г)

[/(0

((-*)

а*

А о =. ' — .

Р (0 л

а, —&/2<*<&/2

О,

К]

> 6/2

2я|х],

1 Л

Ь »

М < ь

6 '

«е

М .

У2

2КУя& |е

йг

УГ г»

1 —

т?~

е йг

У 2л 3

-с

ее ,

(

О, ^<0

2аЬ (

1 — е

)

77 •

0, |<|>&

2а п+2 агсзт

-1)-2агс

ш,|г],

< 2 ь

1 Г

1 —

•

+2агсз1п —Л_

|х|

—

2агс81п >

|х| <

2Ь

—

/ I \

«С05 Г-у "2",

пЬ]

о, \(\ > -у

АаЪ 51п

|г| <

лб

8Ш

26"'

[х|

пб

г)х

X X

Хсов —-|_з№-у .

лЬ

/ < \ , яб

кЬ

0. 1<1>"Г

С М м \

аЪ +

|х| < лЬ

ГЫ , . м

1 — ,

|т|

< пЬ

2 Г

/ С08 ~ \

4 }