Розенберг В.Я. Введение в теорию точности измерительных систем

Подождите немного. Документ загружается.

2. Классы на любом данном уровне не имеют общих элементов

Щ^ПЩ 1:^ = 0' V'». = Г77^ уу. (2.8)

3. Поскольку (2.7) и (2.8) определяют разбиение, элементы (под-

множества) каждого данного множества

связаны между собой отношением эквивалентности.

4. Между связанными классами, расположенными на разных уров-

нях, существует отношение включения (порядка)

Щ гг» С М\ |Д С ... С м\ с ... С м\

(1)

= М, (V). (2.9)

Вместо перебора Д п

—

возможных вариантов при организации

11=1

„списком" (2.5), в данном случае осуществляется направленный поиск

с числом попыток, не превышающим, очевидно, ^ —0- Это, конечно,

гораздо экономней, чем при организации «списком». В частности, при

V —2,

= 1, р имеем двоичное дерево и поиск сводится к дихото-

м и и — на каждом уровне производится всего одно испытание, и, таким

образом, необходимо всего ^ попыток, вместо 2^ — 1.

Вместо выражения (2.5), в данном случае можем записать

М — {т:т — [1(х, а,-),

= (ь, ..., у, 1„=1, л,,

(2.Ю)

— 1, ц, а;

Е=

Л,-}.

Таким образом, конкретную модель можно определить, перечислив

последовательность качественных свойств (значений признаков), отли-

чающих ее от моделей других классов, и указав совокупность количе-

ственных свойств (значений параметров), отличающих ее от других

моделей данного класса. Определение класса можно трактовать как

перечень высказываний (признаков), истинных для данного класса

К ЙГ" = {т:1(1)М (2) Д ... Д

(V)}. (2.11)

Из подобного построения вытекают следующие правила формиро-

вания кодов, терминов и определений понятий:

1. Назовем кодом адреса данного класса г-разрядное число

Я, = «'(1)*(2)...ф), (2.12)

н котором цифра ф„) (А,= 1, V) в каждом разряде соответствует зна-

чению (номеру)

(X) -го признака (или, что то же — номеру класса на

I(Я)-ом уровне иерархии). Тогда код адреса при его чтении слева на-

право указывает направление поиска на каждом очередном шаге при

перемещении по классификационному дереву. Зафиксировать значения

всех признаков — значит выделить конкретную траекторию на класс!

фикационном дереве.

2. Полное наименование данного класса, т. е. соответствующий тер

мин, является словесным обозначением кода адреса и образуется путе!

перечисления признаков при перемещении по дереву (чтении кода адре

са) в обратном направлении. Краткие формы терминов и определенш

образуются путем указания лишь последнего признака /(V) для дан

ного понятия, поскольку из контекста ясно, что оно является частных

случаем (подклассом) более общего понятия.

В дальнейшем мы увидим, что при определенном выборе прпзнако?.

возможно существование классов, соответствующих произвольному чис-

лу возвратных циклов и ветвлений, так что (даже при конечном |л)

число признаков класса может оказаться неограниченным. Этому соот-

ветствует формирование текста произвольной длины из заданного

алфавита. В данном случае чем длиннее оказывается «фраза», состоя-

щая из отдельных высказываний, тем больше сведений она содержит

о классифицируемом объекте.

Во многих случаях, кроме структуры классификационного дерева,

может быть задана дополнительная информация в виде априорных ве-

роятностей Р(1, а.) классов \ и значений параметров а.. В этих случаях

выражения (2.5) и (2.10) соответственно принимают вид

М={т\т = и(х, а,-), Р(1, а,-)}, (2.13)

М = {т:т = (х, а,), Р(1 а.)}, (2.14)

и тезаурус можно рассматривать как множество моделей с заданным

на нем распределением вероятностей (т. е. в виде «пары» (М, Р)).

Наличие априорной вероятности дополнительно сокращает среднее вре-

мя поиска.

Рассмотрим примеры задания параметрических множеств, входящих в (2.5)

или (2.13).

1. .Множество гармонических сигналов с неизвестными параметрами

{т

: т — а

зт (2я^+<р),.(а, (2.15>

или

{т

: т

зт (2я//+ф),

р{а,

I, ф)}. (2.16?

2. Множество стационарных гауссозских процессов с корреляционными функция-

ми вида

или

, К ('): К (') = Е аи ехр (— аъ |

-с

|) сов (Ши тг, т) е К

371

^ (2.17>

(х) : К (х) = 2 «и ехр

(— щ

] х

соз а,-

х,

(<ц

а/

> аи) (2.18)

3. Множество стационарных случайных процессов, вполне определяемых одно-

мерной плотностью вероятностей (так называемый «белый шум»), являющейся элемен-

том параметрического множества

I ( \ I — а

\ )

|р (х) :р(х)= а„ ехр I — \

+ +

й1 \. (л„ а

, а», а

(2.19)

| р(х):р (х) =• ехр

^ —

Дз

^ + ^ )'

(

аи а

Яз

а4

' /*

Здесь выражение, определяющее р

^), является решением дифференциального уравне-

ния Пирсона

ёр{{)__

((

—

а)

<11 Яз а4 + а4

и включает в себя гауссовское, пуассоновское, гамма-распределения и ряд других. За-

метим, что множество {р{х)} можно задать также «отрезком» ряда Эджворта, так на-

зываемым «экспонентным семейством» и некоторыми другими способами.

Таким образом, объектом классификации служат модели т, являю-

щиеся элементами полного множества М моделей. Признаки I

и параметры суть те характеристические свойства исследуемого объ-

екта, которые надлежит установить путем измерительного эксперимента.

Априорная вероятность Р(1, а.г) описывает действие основного вероятно-

стного механизма ВМ

(см. рис. 1.6).

Из (2.6) следует, что задача организации тезауруса с иерархиче-

ской структурой состоит в выделении последовательности н, ..., I

признаков, после чего определяется совокупность параметрических

множеств вида (2.10) или (2.14). Разумеется, система признаков,

используемая при классификации моделей, определяется конкретной

областью исследований, для которой создается тезаурус, а также со-

стоянием теории в этой области.

В настоящее время, наряду с дифференциацией наук, наблюдается тенденция

к их синтезу на основе общих методологических концепций. Это обстоятельство, в част-

ности, находит проявление во все более широком использовании в различных областях

вероятностных моделей исследуемых объектов. Построение вероятностных моделей

производится на основе разработанной А. Н. Колмогоровым аксиоматики теории веро-

ятностей. Тот факт, что аксиоматические построения теории вероятностей обнаруживают

весьма полное соответствие условиям проведения измерительного эксперимента, объяс-

няется не счастливым стечением обстоятельств, а тем, что теория вероятностей является

аппаратом *>, разработанным специально для обработки опытных данных с целью по-

лучения определенных выводов на основе наблюдений, получаемых в эксперименте со

случайным исходом, т. е. при наличии неконтролируемых влияющих факторов. В соот-

ветствии с этим в теории вероятностей исходят из следующих положений.

Прежде всего вводится представление о множестве (пространстве) й эле-

ментарных событий соей, каждое из которых отождествляется с исходом

одного эксперимента.

Далее, выделяются подмножества Ей (г=1, 2, ...), называемые события-

м и, причем такие, что теоретико-множественные операции, производимые над этими

подмножествами в счетном числе, образуют подмножества, которые также являются

событиями. Совокупность таких подмножеств .(включая само Й, называмое достовер-

*' Теорию вероятностей иногда рассматривают как раздел теории меры, являю-

щейся, в свою очередь, разделом теории множеств [72].

ным событием и пустое множество 0, называемое невозможным событием) назы-

вается а-алгеброй и обозначается буквой . Таким образом, имеем

/=1

Наконец, каждому событию ставится в соответствие неотрицательное число

Р (•Л)' называемое вероятностью этого события (вероятностной мерой),

причем такое, что

/>(а) = 1, Я(0) = о

и, если М П -А} = 0 («. / = 1. 2,...\ьф /), то

( = 1

Последнее условие называется условием счетной аддитивности.

Таким образом, вероятностная модель задается тройкой

(2. Р)г (2.21>

называемой вероятностным пространством, в которой й — любое множе-

ство рассматриваемых элементарных событий, еГ — некоторая 0-алгебра подмножеств

множества О, Р — счетно-аддитивная вероятностная мера, определенная на ,

Система признаков, выбираемая при классификации вероятностных моделей, должна

учитывать всевозможные виды вероятностных пространств. При этом должна получиться

тройка векторов (1

, \

), каждый из которых представляет собой последовательности

признаков соответствующих элементов О, <•?*, Р, образующих в совокупности вероят- '

постное пространство. Поскольку вид о-алгебры ёГ определяется конкретными особен-

ностями решаемой задачи, мы ограничимся рас-

смотрением признаков, связанных только с мно-

жеством {2 элементарных событий и вероятност-

ной мерой Р. В приложениях теории случайных

процессов [68] последние определяются как ан-

самбль реализаций (множество Й) с заданным

на нем вероятностным распределением (мера Р),

без указания особенностей о-алгебры &Г.

Так как в дальнейшем предполагается, что

исследуемые объекты могут быть описаны моделя-

ми случайных процессов (что соответствует доста-

точно широкому классу объектов), целесообразно

придерживаться аналогичной методики.

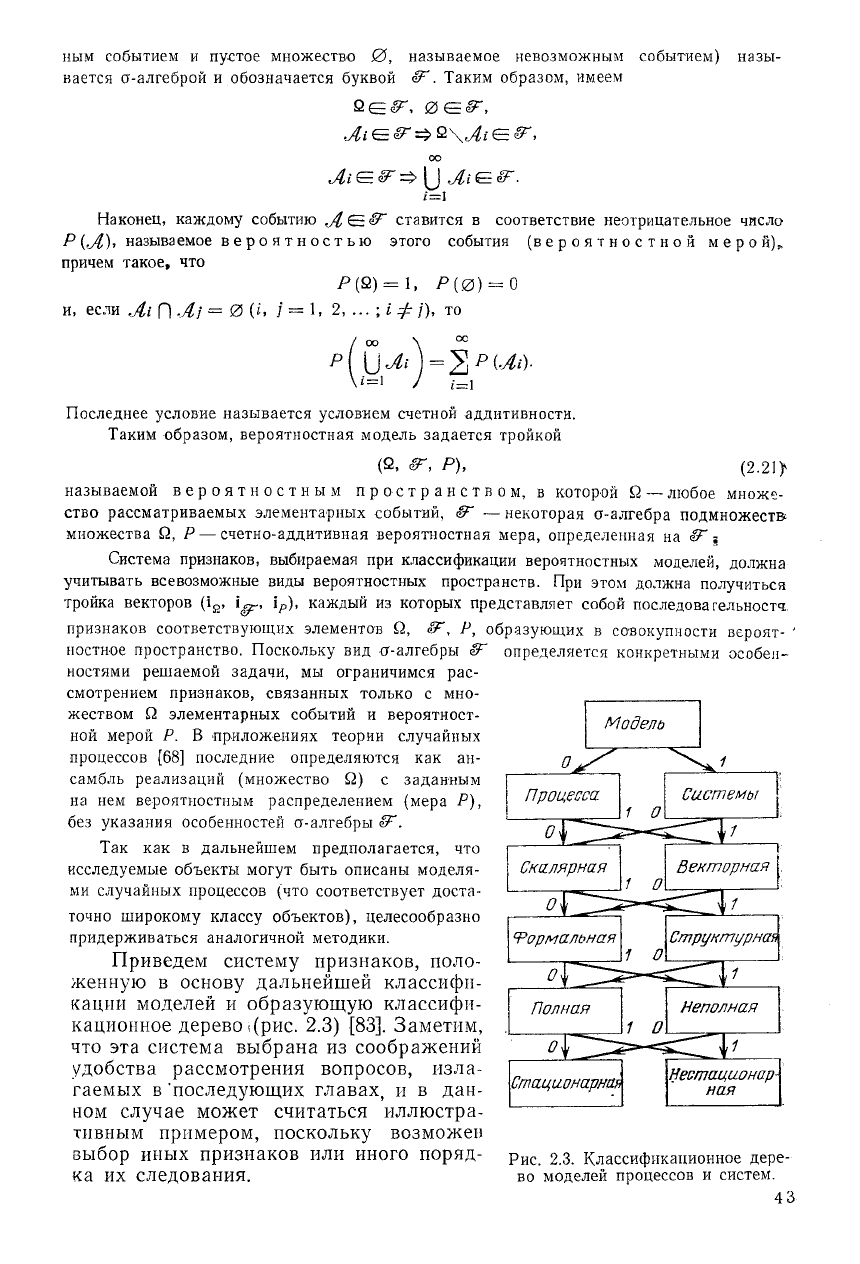
Приведем систему признаков, поло-

женную в основу дальнейшей классифи-

кации моделей и образующую классифи-

кационное дерево I(рис. 2.3) [83]. Заметим,

что эта система выбрана из соображений

удобства рассмотрения вопросов, изла-

гаемых в 'последующих главах, и в дан-

ном случае может считаться иллюстра-

тивным примером, поскольку возможен

выбор иных признаков или иного поряд-

Рис

2.3. Классификационное дере-

ка их следования. во моделей процессов и систем.

1. Наряду с «обычными» процессами х(Ь) будем рассматривать

двухкомпонентные процессы (упорядоченные пары процессов) вида

(1)> У(1))> называемые системами, причем компонента х(1) будет

именоваться входным процессом, а компонента у{1)—выходным. Каж-

дая из компонент может быть как скалярной, так и векторной.

Модели процессов используются для описания физических величин

(таких, как напряжение, ток, температура, давление), зависящих от

времени, пространственных и других координат; модели систем — для

описания совокупностей процессов, объединяемых по признаку наличия

причинно-следственных связей между ними (х(1)—«причина», у(1) —

«следствие»), таких, например, как каналы связи, измерительные при-

боры, преобразователи, управляющие устройства, искусственно, создан-

ные для достижения определенной цели. Понятие «система» иногда

удобно трактовать как оператор, устанавливающий соответствие меж-

ду входные и выходным процессами.

2. Далее выделим скалярные и векторные модели процессов и си-

стем. Скалярные модели описывают простейшие объекты: процесс,

развиваемый на данной паре зажимов, систему с одним входом и одним

выходом. Векторные модели описывают более сложные объекты:

совокупность процессов, действующих на различных парах зажимов,

системы, имеющие более чем по одному входу и (или) выходу.

Если изучение векторной модели можно свести к изучению сово-

купности скалярных моделей или векторных моделей с меньшим чис-

лом компонент, то такую модель мы будем называть сепарабель-

н о й.

3. Если в распоряжении исследователя имеется априорная инфор-

мация о структуре объекта, например, о механизме образования про-

цесса или внутренней организации системы, то эта информация, как

правило, должна быть использована при построении модели. Тогда

и зависимости от того, имеется (используется ли) или отсутствует (не

используется) такая информация, модели можно подразделить соот-

ветственно на структурные и формальные.

Структурные модели, описывающие структуру объекта, выра-

жаются тем или иным образом через совокупность других моделей,

благодаря чему появляется возможность управления объектом.

Формальные (феноменологические, диффузионные, плохо орга-

низованные *>) модели, определяемые, как случай, альтернативный

предыдущему, описывают явление без проникновения в его сущность.

Такое описание, как правило, является весьма громоздким и не содер-

жит указаний на возможности управления объектом.

4. Целесообразно выделить так называемые полные и неполные

модели. Полные модели определяются в общем случае вероятностной

?»;ерой, заданной на пространстве реализаций процесса или системы.

Неполные модели определяются не вероятностной .мерой, а одной

или несколькими вероятностными характеристиками, представляющими

собой результат невзаимио-однозначного преобразования меры, так что,

располагая этими характеристиками, невозможно вновь «воссоздать»

меру.

Модели (полные или неполные), связанные между собой взаимно-

однозначными преобразованиями, назовем эквивалентными.

Последние два термина заимствованы из работы [44].

5. Последний признак характеризует инвариантность или неинва-

риантность вероятностной меры или отдельных вероятностных харак-

теристик по отношению к оператору сдвига аргумента на произвольную

величину т. В соответствии с этим определяются стационарные

(инвариантные, однородные) и нестационарные (неинвариантные,

неоднородные) модели.

Попутно мы будем обсуждать детерминированные (регуляр-

ные) модели, которые являются частным случаем вероятностных

(стохастических) и получаются в предположении, что вся вероятност-

ная мера сосредоточена в одной точке ю* (на данной траектории

х(-, со*)). Этот факт может быть использован в качестве дополнитель-

ного признака, который мы, однако, специально выделять не будем.

Первые три признака характеризуют, очевидно, пространство эле-

ментарных событий О (признаки 1

), остальные признаки-—вероятност-

ную меру Р (признаки 1р). Указанные признаки порождают классифи-

кационное дерево, обладающее дихотомической структурой (двоичное

дерево), причем для задания кода адреса (1.12), соответствующего

классу, находящемуся на нижнем уровне иерархии, достаточно указать

пятизначное число (в соответствии с выбранным количеством призна-

ков) в двоичной системе счисления. Цифра в каждом разряде указы-

вает направление движения по классификационному дереву, а также

является сокращенным обозначением соответствующего термина. На-

пример, код 00110 соответствует стационарной (0) неполной (1) струк-

турной (1) скалярной (0) модели процесса (0).

В действительности оказывается, что для каждого из указанных

классов можно выделить дополнительные признаки, из-за чего класси-

фикационное дерево приобретает более сложную структуру.

2.2. МОДЕЛИ ПРОЦЕССОВ

(0) Модели процессов определяются совокупностью признаков, вы-

деляющих из всевозможных множеств множество функций, т. е. функ-

циональное пространство. Кроме того, предполагается, что конкретная

функция — элемент этого пространства — является результатом наблю-

дения в некотором эксперименте, имеющем, вообще говоря, случайный

исход. Поэтому данный класс можно определить выражением

Мо={хУ, со) : х<=Х, соей}. (2.22)

Таким образом, признаки класса состоят в том, что Т (область

определения процесса) и X (область значений процесса) суть числовые

множества (или векторные пространства) и каждому элементу /еГ со-

ответствует (см. § 1.2) единственный элемент Множество Охарак-

теризует «запас точек» множества М

. Действительно, функцию х(1, со)

можно считать функцией двух аргументов I и со. Если зафиксировать

аргумент (, обычно имеющий смысл времени, получим х((, •) —случай-

ную величину (скалярную или векторную); если же зафиксировать со,

играющее роль «случая», получим х(-, со) —функцию I, называемую

реализацией процесса (выборочной функцией, траекторией). В дальней-

шем знак со иногда будем опускать и обозначать х(-, ш)Ах(/).

Дополнительные предположения, регламентирующие те или иные

особенности множеств Т и X, позволяют выделить подклассы данного

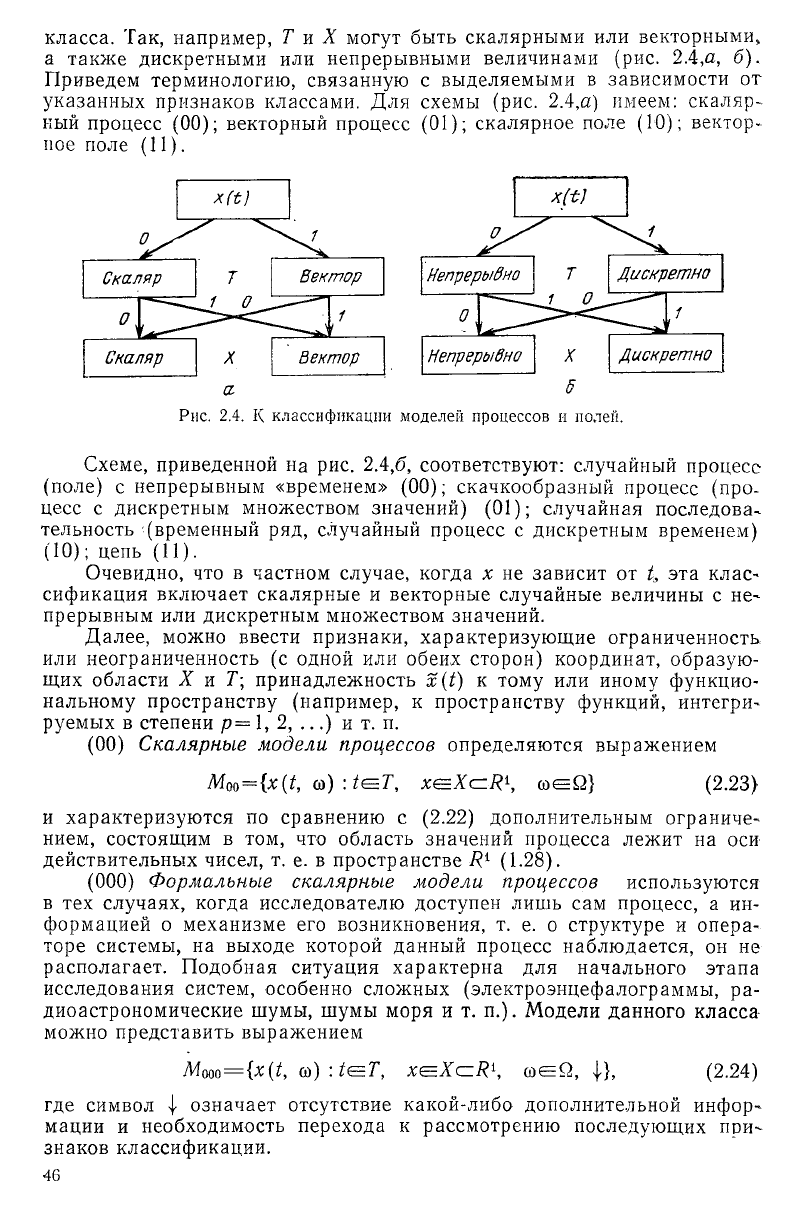
класса. Так, например, Т и X могут быть скалярными или векторными,

а также дискретными или непрерывными величинами (рис. 2.4,а, б).

Приведем терминологию, связанную с выделяемыми в зависимости от

указанных признаков классами. Для схемы (рис. 2.4,а) имеем: скаляр-

кый процесс (00); векторный процесс (01); скалярное поле (10); вектор-

ное поле (11).

Вектор

Непрерывно

Дискретно

Вектор

Непрерывно

Дискретно

Рис. 2.4. К классификации моделей процессов и полей.

Схеме, приведенной на рис. 2.4,6, соответствуют: случайный процесс

(поле) с непрерывным «временем» (00); скачкообразный процесс (про-

цесс с дискретным множеством значений) (01); случайная последова-

тельность (временный ряд, случайный процесс с дискретным временем)

(10); цепь (11).

Очевидно, что в частном случае, когда х не зависит от I, эта клас-

сификация включает скалярные и векторные случайные величины с не-

прерывным или дискретным множеством значений.

Далее, можно ввести признаки, характеризующие ограниченность

или неограниченность (с одной или обеих сторон) координат, образую-

щих области X и Г; принадлежность х(1) к тому или иному функцио-

нальному пространству (например, к пространству функций, интегри-

руемых в степени р= 1,2,...) и т. п.

(00) Скалярные модели процессов определяются выражением

Моо=№ со) : *е=7\ хевХ<=Я\ соей} (2.23)

и характеризуются по сравнению с (2.22) дополнительным ограниче-

нием, состоящим в том, что область значений процесса лежит на оси

действительных чисел, т. е. в пространстве Я

(1.28).

(000) Формальные скалярные модели процессов используются

в тех случаях, когда исследователю доступен лишь сам процесс, а ин-

формацией о механизме его возникновения, т. е. о структуре и опера-

торе системы, на выходе которой данный процесс наблюдается, он не

располагает. Подобная ситуация характерна для начального этапа

исследования систем, особенно сложных (электроэнцефалограммы, ра-

диоастрономические шумы, шумы моря и т. п.). Модели данного класса

можно представить выражением

= {х{1, со) : *е=7\ жеХс^, СОЕЕЙ, (2.24)

где символ | означает отсутствие какой-либо дополнительной инфор-

мации и необходимость перехода к рассмотрению последующих при-

знаков классификации.

(0000) Полные формальные скалярные модели процессов определя-

ются как подмножество множества Мт, выделяемое путем дополни-

тельного указания вероятностной меры Р

А/

0000

= {*(*, со) :/<=2\ соеО, Р}. (2.25)

Таким образом, рассматриваемый класс есть класс вероятностных мо-

делей, т. е. моделей, вполне определяемых заданием вероятностного

пространства (2.21).

Вероятностную меру Р можно задать различными способами

[66 ... 68], используя: функционал вероятности, функционал плотности

вероятности, характеристический функционал, бесконечную последова-

тельность конечномерных распределений. Поскольку используемые

в этих способах функции связаны между собой (взаимно-однозначными

преобразованиями, постольку получаемые этими способами модели

оказываются эквивалентными друг другу.

В последнем способе, получившем наибольшее распространение на

практике, случайный процесс рассматривается как семейство случайных

величин {Х{, {(ЕТ} С заданными конечномерными функциями распределе-

ния Р

(х,,..., х, ) систем случайных величин х.,...,х. для любого ко-

нечного множества значений так что

•Моооо=

уга = 1, 2,...; у/„ ...Лп€=Т-,зР

(х

, (2.26)

Здесь функция Р

(х

{

, ..., Х

), называемая «-мерной функцией распре-

деления случайного процесса, имеет смысл вероятности пребывания

случайного вектора х= (х

(

,..., х

(

) ниже фиксированного векторного

уровня х = ..., х

(

Рп(х

,... ,х^ = Р$

(

<х

,...,х

{

<х^ (2.27)

и (по определению) удовлетворяет условиям

0<Р

(х

(

, ...,х

(

)<1, (2.28)

'» ы

Рп (х±,..., х. ) = Р

(х. ,..., х. ), (2.29)

1 1

П 1

»„

где н, г

, ..1

— любая перестановка индексов 1, п;

(х

,..., х

) = Р

{х

,..., X; , 4~оо,... ,+оо), ут6{1, га —1}.

(2.30)

Условие (2.29) называется условием симметрии, условие (2.30) —

условием согласованности.

Вместо функции Р„ (х

(

,..., х

(

) в (2.26) можно использовать функ-

цию р

..«, х

(

) (если она существует), называемую га-мерной плот-

ностью вероятностей случайного процесса, имеющую смысл вероят-

*> Напомним, что вероятностная мера Р, в свою очередь, определяется на сг-алгеб-

рг г?" подмножеств множества О элементарных событий.

ности попадания векторной величины х = (х^,..., х

(

) в векторный эле-

ментарный интервал дх = (дх,,..., дх, )

'п.

др

п {х

(

)

(х

(

,..., х, ) =

д д

• (2.31)

*1 '

Для этой функции справедливы условия: неотрицательности

(х

{

,...,х

(

)>0, (2.32)

нормировки (ср. с (2.28))

оо

Г... [р„(х

{

, ...,х

(

)с1х

{

...йх

= 1, (2.33)

Л Л

—ос —со

симметрии (ср. с 2.29)

Рп

(х,,..., х

(

) =

Рп

(Х

(

.,..., х

(

. ), (2.34)

" '» 'я

согласованности (ср. с 2.30)

ОО 00

Рт{х. , ... , Х{ ) \ ... I рп {Х{ , ... , X. , X. , ... , X, ).

т .! л «1 'т '/п+1 л

—00 —00

йх, ... йх, п—\\. (2.35)

.1 + 1 Л

п-мерная характеристическая функция случайного процесса пред-

ставляет собой /г-кратное преобразование Фурье от р

{х

, ...,

Л'

00 оо

(ш„ ...,

/&„)

= ... \ р„ (л*,,..., л, ) е йх

... йх^.

—00 —эо

(2.36)

Практическое применение моделей вида (2.26), требующих использования беско-

нечной последовательности функций Р

(х^, . . ., х

(

); р

(х^ х ) или 9

('Уь •• •

...,

) для любых п связано с рядом трудностей. Поэтому на практике чаще всего

рассматривают подклассы данного класса моделей, выделяемые путем введения допол-

нительных предположений. Например, используют так называемый процесс п-го по-

рядка, т. е. процесс, вполне определяемый своими га-мерными функциями распределения,

но не определяемый функциями распределения порядка п—1

{х{1,

о>)

: ул, уПеТ, Г

(х

, ... ,х,

)}. (2.37

Дальнейшую классификацию этих моделей можно построить в зависимости от

значения п:

при я=1 имеем процесс 1-го порядка (абсолютно случайный процесс, «белый

шум», процесс с независимыми значениями)

о>):ул, уП^Т, р

{х

(

, ... , х

(

) = Пр! (XI, (2.38}

" 1=1 )

при п—А — процесс !!-го порядка

\ х со): утг, Рп (Х

{

, ... , Х

{

) =

Р1

(Хг, Л) ГУ р{Х1, | Х/_,, > (2.39)

I " 1=2 )

(где р(Хг, 1дгг—1, ^1-1)—условная плотность вероятности) и т. д.

Частным, но весьма важным случаем процессов 2-го порядка является гауссов-

ский процесс, однозначно определяемый (обязательно нормальной) двумерной плотно-

стью вероятностей (и, следовательно, корреляционной функцией (2) и математиче-

ским ожиданием)

х (/, со) :

= 1, п, ул, рп (х^, ... ,х

(

)

= (2ъ)~

п12

(йе1Я)

112

ехр

-0,5 ^

VI!

(XI -

М{)

(х/ -

М})

1,7=1

(2.40>

где №ч=М{х('ч)}\ У= ||— матрица, обратная корреляционной матрице В =

= ||/?(<1, {])

11,

т. е. подчиняющаяся уравнению

УИгЯк!

ОЦ,

к= 1

где

1 1 при I = /

с,-/ — < — символ Кронекера.

( 0 при I ф /

Рассматриваемый класс включает в себя также детерминирован-

ные (абсолютно неслучайные, регулярные) процессы, которые опреде-

ляются дополнительным условием, состоящим в том, что вся вероятно-

стная мера сосредоточена на одной траектории х*{1) (или, что то же,,

в данной точке и* пространства элементарных событий Й, которое

является единичным множеством, содержащим лишь эту точку). По-

этому значения детерминированного процесса для любого момента вре-

мени известны с вероятностью единица. Это условие можно описать

выражением

М0:ур

(х

) = Ь(х — х

)}, (2.41),

где б(-)—дельта-функция, которое служит определением «контину-

альной 6-функции».

С другой стороны, случайный процесс определяется выражением

(ср. с (2.26))

{*(*): Рг(хЛфЬ(х

—

Хг)}. (2.42),

Таким образом, повторение наблюдений детерминированного про-

цесса приводит к одному и тому же результату, а случайного — к раз-

ным результатам. Детерминированный процесс можно описать извест-

ной функцией 8(1)

{х

({):

(- °°,

<*>);

(/)

5 (0} •

(2.43>

Эта запись отражает тот факт, что детерминированный процесс пред-

ставляет собой единственный тип процесса, временное описание кото-

рого совпадает с его «любой реализацией» на всей временной оси, вви-

4—96 45>