Розенберг В.Я. Введение в теорию точности измерительных систем

Подождите немного. Документ загружается.

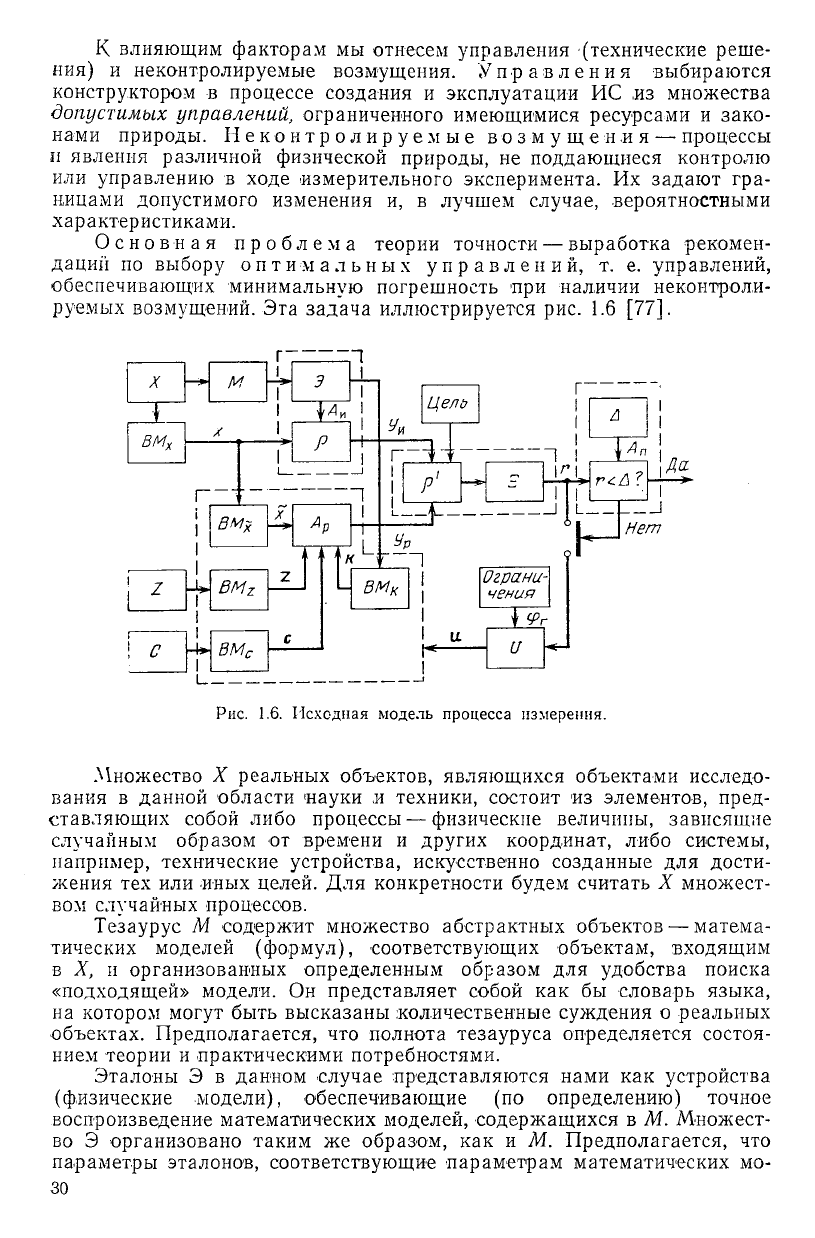
К влияющим факторам мы отнесем управления (технические реше-

ния) и неконтролируемые возмущения. Управления выбираются

конструктором в процессе создания и эксплуатации ИС из множества

допустимых управлений, ограниченного имеющимися ресурсами и зако-

нами природы. Неконтролируемые возмущения—-процессы

и явления различной физической природы, не поддающиеся контролю

или управлению в ходе измерительного эксперимента. Их задают гра-

ницами допустимого изменения и, в лучшем случае, вероятностными

характеристиками.

Основная проблема теории точности — выработка рекомен-

даций по выбору оптимальных управлений, т. е. управлений,

обеспечивающих минимальную погрешность при наличии неконтроли-

руемых возмущений. Эта задача иллюстрируется рис. 1.6 [77].

Рис. 1.6. Исходная модель процесса измерения.

Множество X реальных объектов, являющихся объектами исследо-

вания в данной области науки ,и техники, состоит из элементов, пред-

ставляющих собой либо процессы — физические величины, зависящие

случайным образом от времени и других координат, либо системы,

например, технические устройства, искусственно созданные для дости-

жения тех или иных целей. Для конкретности будем считать X множест-

вом случайных процессов.

Тезаурус М содержит множество абстрактных объектов — матема-

тических моделей (формул), соответствующих объектам, входящим

в X, и организованных определенным образом для удобства поиска

«подходящей» модели. Он представляет собой как бы словарь языка,

на котором могут быть высказаны количественные суждения о реальных

объектах. Предполагается, что полнота тезауруса определяется состоя-

нием теории и практическими потребностями.

Эталоны Э в данном случае представляются нами как устройства

(физические модели), обеспечивающие (по определению) точное

воспроизведение математических моделей, содержащихся в М. Множест-

во Э организовано таким же образом, как и М. Предполагается, что

параметры эталонов, соответствующие параметрам математических мо-

делен, можно (варьировать в необходимых пределах, причем их значения

при этом остаются известными, подобно тому, как это имеет место

в многозначных мерах.

Заметим, что в идеальном (гипотетическом) случае множества X,

М, Э считаются эквивалентными. Таким образом, цепочка X — М — Э

(материальное — абстрактное — материальное) преобразует элементы

множества исследуемых объектов в элементы множества известных

объектов. Например, если

А'

— множество физических свойств реального

внешнего мира, характеризуемых некоторыми константами, то М—си-

стема единиц, не исчерпывающая, в силу ограниченности физических

законов, всего многообразия этих свойств, а Э — множество первичных

эталонов этих единиц. Другой пример: X — множество реальных случай-

ных процессов, М — справочник по теории случайных процессов, Э —

множество соответствующих измерительных генераторов эталонных слу-

чайных процессов с регулируемыми и контролируемыми параметрами.

При проведении измерительного эксперимента имеют дело с одним

вполне конкретным исследуемым объектом — элементом х из множества

X, причем неизвестно, с каким именно. Это обстоятельство мы предста-

вим в виде действия некоторого вероятностного механизма ВМ*, «выби-

рающего наудачу» некоторый элемент ВМ

мы будем далее на-

зывать основным вероятностным механизмом, поскольку

он определяет смысл измерительного эксперимента, заключающийся

в том, что необходимо идентифицировать х с одним из эталонов с опре-

деленными значениями параметров, а отсюда — и с конкретной мо-

делью, содержащейся в М.

Идеальная система, представляющая собой гипотетическое

устройство, описываемое оператором А

, сравнивает с помощью опера-

тора компарирования р по алгоритму (1.31) данный исследуемый

объект х со всеми эталонами из множества Э, выбирая из них тот, кото-

рый близок к х в смысле критерия р. Порядок поиска этого эталона

определяется способом организации множества Э. Предполагая, что

множества X, М, Э эквивалентны, замечаем, что в силу аксиомы тож-

дества (1.26) и отсутствия влияющих факторов, результат измерения

г/„ — модель объекта х — будет свободен от погрешностей. Заметим так-

же, что при фиксированном х результат измерения у

не случаен, т. е..

идеальная система является детерминированной.

Реальная система (с оператором Л

) представляет собой

устройство, содержащее меру и компаратор. Ее необходимо описывать

моделью, учитывающей наличие влияющих факторов. С этой целью мы

вводим в рассмотрение возможные управления и (вариант схемы, конст-

рукции, регламента обслуживания и т. п.), выбираемые из допустимого

множества V, ограниченного имеющимися ресурсами ?

, а также не-

контролируемые возмущения, исходы действия которых в процессе дан-

ного измерительного эксперимента определяются соответствующими

вероятностными механизмами (ВМ). К числу факторов, оказывающих

неконтролируемые воздействия на результат измерения, мы отнесем:

— ограниченность числа и (или) длительности доступных для наб-

людения реализаций исследуемого процесса, в результате чего в кон-

кретном измерительном эксперименте мы имеем дело не с самим иссле-

дуемым процессом (ансамблем реализаций), а с отдельными реализа-

циями х(1), появлением которых управляет вероятностный механизм

ВМ~, определяющий статистический характер проблемы измерения;

— действие внешних неконтролируемых процессов (темпера-

тура, давление, влажность и т. п.), влияющих на элеметы ИС и изме-

няющихся во времени непредвиденным образом; реализации г(1) «вы-

бираются» вероятностным механизмом ВМ

;

— отклонение значений параметров с(/) элементов ИС от номина-

ла в результате неизбежного технологического разброса, естественных

процессов старения, окисления и т. п., из-за чего эти значения с изме-

няются во времени и от одного экземпляра ИС данного типа к другому,

что учитывается включением вероятностного механизма ВМ

;

— отклонение значений параметров рабочей меры, имеющейся

в составе ИС, от номинала, вызванное несовершенством системы пере-

дачи размеров единиц от эталонов через последовательность образцо-

вых средств измерений, соответствующую принятой поверочной схеме,

к данному рабочему прибору. Отклонение имеет случайный характер

из-за действия влияющих факторов на образцовые и рабочие средства

в процессе передачи, что можно описать с помощью действия вероят-

ностного механизма ВЛ1ь. С действием этого вероятностного механизма

мы свяжем также неполноту реально используемого тезауруса (несо-

вершенство теории), что эквивалентно наличию неизмеряемых парамет-

ров исследуемого процесса.

Таким образом, мы полагаем, что имеются два «полезных» входа —

один «явный», на который подается исследуемый процесс, и другой —

«неявный», по которому в ИС вводится информация от эталонов. Кроме

того, считаем, что ИС имеет «паразитные» входы, связанные с осталь-

ными влияющими факторами.

В результате воздействия влияющих факторов при фиксированном

х результат измерения г/

в реальной ИС, в отличие от результата

измерения у

в идеальной ИС, случаен, т. е. реальная ИС является

стохастической.

Погрешность измерения можно трактовать как результат

сравнения в соответствии с некоторым критерием р', указанным в нор-

мативном документе или зависящим от цели измерения, выходных сиг-

налов идеальной у

и реальной у

систем. Погрешность измерения пред-

ставляет собой число (значение функционала).

Как уже отмечалось, при многократном повторении измерения (при

фиксированном х) показание г/

идеальной системы остается одним

л тем же, а показание у

реальной системы изменяется случайным

образом из-за наличия случайных механизмов ВМ~, ВМ&, ВМ

, ВМ

являющихся источниками погрешности. Поэтому погрешность измерения

есть случайная величина, которая, естественно, полностью характери-

зуется своим законом распределения. Оператор 3 ставит в -соответствие

этому закону некоторую числовую характеристику — погрешность

системы г или погрешность типа систем Я. Эти величины

можно определить как при фиксированном жеХ (условная по-

грешность), так и на всем множестве X (безусловная по-

грешность). В последнем случае они характеризуют метрологиче-

ское качество системы или типа систем на -всем множестве возможных

применений.

Допустимый уровень качества данной системы регламентируется

требованиями «потребителей» и количественно выражается значением

допуска Д. Оператор контроля (поверки) А

, сравнивая г и Д,

вырабатывает решения «годен» (г<Д) или «не годен» (г^Д). (В про-

::?ссе контроля роль идеальной системы играет образцовая система.)

Решение «не годен» — сигнал к дальнейшему усовершенствованию си-

стемы, путем выбора оптимального управления и*<=11 в соответствии

с алгоритмом (1.35). Решение «годен» — сигнал к эксплуатации.

Перейдем к обсуждению этой схемы в целом, а также вариантов,

зытекающих из нее как частные случаи при некоторых упрощающих

предположениях. Отметим вначале, что ее можно описать в терминах

теории информации, если трактовать тезаурус как алфавит языка, на

котором передается сообщение, идеальную систему — как канал без

шумов, а реальную — как канал с шумами. В идеальной системе

априорная неопределенность снимается полностью и объект безошибоч-

но идентифицируется с конкретным элементом тезауруса. Количество

получаемой при этом информации зависит от объема тезауруса и равно

начальной энтропии. Реальная система снимает не всю неопределен-

ность, поскольку она подвержена действию вероятностных механизмов

ВЛ1~,ВМй, ВМ

, ВМ*. Остаточная неопределенность рассматривается

к::к погрешность системы.

Далее, рассматривая различные множества X, соответствующие той

или иной области науки и техники (механика, радиотехника, химия,

идерная физика, акустика, медицина и т. д.), можно интерпретировать

результаты исследования этой модели применительно к разным видам

измерений (соответственно, механических, радиотехнических, химиче-

-•;;их, параметров ионизирующих излучений, акустических, медицинских

: т. д.). Следует учесть, чуо структура математических моделей, вхо-

дящих в тезаурус, для различных областей может оказаться одинако-

вой (известно, например, что теория случайных процессов развивается

:ак математическая дисциплина, инвариантная, как и всякий другой

раздел математики, к физической природе рассматриваемых процессов).

Практические последствия этого обстоятельства трудно переоценить:

поскольку процессы различной природы с помощью первичных преобра-

зователей можно получить в форме процесса единой природы (пред-

почтительно— электрической), возможна чрезвычайно широкая унифи-

кация методов и средств измерений, оценки погрешностей, образцовых

и эталонных средств, поверки и т. п., при условии, что алгоритмы обра-

ботки реализуются средствами радиоэлектроники.

Теория точности должна охватывать в рамках единого построения

как комплексные, так и элементарные статистические измерения, без-

относительно к тому, в какой области эти задачи возникают.

В отличие от детерминированных измерений, которые не будут

дялее изучаться, мы говорим о статистических измерениях, имея

при этом в виду, что действие всех вероятностных механизмов (см.

рис. 1.6) описывается в вероятностных терминах.

Уточним, что под комплексным измерением мы понимаем

измерение, имеющее целью:

— выбор вида математической модели исследуемого объекта (за-

дача проверки гипотез о виде модели);

— определение числовых значений параметров этой модели (зада-

ча «собственно» измерений или оценки параметров);

— количественную оценку степени адекватности выбранной модели

.^следуемому объекту.

К элементарным статистическим измерениям следует, например,

отнести:

->—96

1. Принятие решения (без оценки параметров). К этому классу

измерительных задач относятся задачи распознавания образов, обнару-

жения объекта (сигнала в шуме), контроля систем, технической диаг-

ностики. В математической статистике эти задачи известны как задачи

проверки гипотез.

2. Оценку векторного параметра (без принятия решения о виде

математической модели). Это наиболее разработанный класс «собствен-

но измерительных» задач. В этом случае считается, что состояние ВМ

фиксировано и известно, и рис. 1.6 иллюстрирует задачу анализа и опти-

мизации некоторого конкретного прибора.

3. Оценку скалярной величины — частный случай предыдущей зада-

чи — включающую в себя такие виды измерений, как измерение тока,

напряжения, частоты, коэффициента нелинейных искажений, мощности

шума.

4. Воспроизведение реализации случайного процесса в координатах

«физическая величина — время», причем значения этих координат вы-

ражены в принятых единицах. Примерами систем, реализующих задачи

такого рода, являются аналого-цифровые преобразователи, самописцы,

эле ктр ока р д и о гр а ф ы.

5. Воспроизведение характеристик процессов и систем в соответст-

вующих координатах. Системы подобного рода — панорамные анализа-

торы спектра, законов распределения, характернографы, измерители

переходных и частотных характеристик.

6. Воспроизведение характеристик в дискретных точках, реали-

зуемое, например, анализаторами при многоканальном одновременном

анализе.

Вполне очевидно, что элементарные измерения являются либо составными частя-

ми, либо частными случаями комплексного измерения. Действительно, если представ-

ляет интерес только вид модели, то схема описывает процесс распознавания образов.

В частности, в процессе контроля Л

играет роль образцовой системы, а Л

— пове-

ряемой.

С другой стороны, задача оценки параметров возникает лишь тогда, когда харак-

тер модели установлен. В противном случае неясно, о каких параметрах идеть речь.

Воспроизведение реализаций исследуемого процесса можно рассматривать как

вспомогательную, промежуточную задачу в собственно измерениях, поскольку реализа-

ция процесса лишь материал для получения результата измерения, но не сам резуль-

тат. При оценке точности произвольного преобразования оператор Л„ описывает желае-

мое преобразование, а представляет собой реальный преобразователь. Соответст-

венно этому у

— неискаженный, а у

— искаженный сигналы, г — мера искажений. При

этом можно оценивать точность усилителей, функциональных преобразователей, филь-

тров, приемников, измерительных устройств, предназначенных для воспроизведенич

реализаций и характеристик случайного процесса, аппроксиматоров и других систем.

Исследуемыми объектами в теории точности являются:

— измерительная система произвольного назначения (для ком-

плексных или элементарных статистических измерений в различных

областях) и ее субсистемы (блоки, модули, элементы);

— тип измерительных систем произвольного назначения и типы

субсистем;

— множество типов измерительных систем и субсистем, образую-

щих всю измерительную технику — «приборное хозяйство» страны.

Основная проблема теории точности (задача синтеза)

формулируется применительно к любому из этих объектов как задача

оптимизации (1.35)

и* = аг^ тт §1 (и), (1.39)

и(=С>

(где ^-—погрешность ИС (типа ИС, множества типов ИС); II—мно-

жество допустимых управлений, ограниченное заданными ресурсами;

и* — оптимальное управление), в предположении, что о множестве не-

контролируемых возмущений имеется априорная информация.

Например, при оптимизации множества типов измерительных си-

стем это выражение описывает, грубо говоря, предельную эффективность

усилий, направленных на совершенствование измерительной техники,

выраженную величиной народнохозяйственного эффекта, полученного

от применения измерительной техники к единице затрачиваемых

средств.

Согласно концепции управления (см. рис. 1.3,в) решение основной

проблемы предусматривает: выбор критерия решение задач анализа

и синтеза.

Задача анализа состоит в построении модели объекта (1.31),

учитывающей основные источники погрешности. Такими

источниками, например, согласно схеме рис. 1.6, являются:

— несовершенство теории (неполнота тезауруса М);

— несоответствие (неэквивалентность) множества Э эталонов мно-

жеству М моделей;

— несовершенство системы образцовых средств к;

— неоптимальность решений (управлений) и, применяемых на всех

этапах создания и эксплуатации ИС;

— наличие ограничений, регламентирующих множество V возмож-

ных решений;

— ограниченность объема наблюдений х;

— воздействие на ИС внешних влияющих факторов г;

— разброс относительно номинала и нестабильность во времени

параметров элементов с, из которых собирается ИС;

— неадекватность критерия р решаемой задаче (при неавтономном

использовании ИС).

Цель анализа—выявить подобные источники погрешности и опре-

делить ее составляющие, т. е. «вклад», вносимый каждым источни-

ком и их произвольной комбинацией в «полную» погрешность.

Цель синтеза— изыскать пути воздействия на указанные источники

для уменьшения составляющих — в первую очередь тех, которые играют

доминирующую роль. Из сказанного следует, что рекомендации теории

точности затрагивают сферы разработки теории, проектирования,

производства и эксплуатации ИС. Они также представляют интерес

при постановке конкретного измерительного эксперимента и оценке

достоверности его результатов, при реализации конкретного типа ИС,

лри планировании развития измерительной техники. В частности, при-

ступая к экспериментальному исследованию, специалист неизменно

сталкивается с вопросами, касающимися

— цели измерения (для чего измерять?);

— объекта измерения (что измерять?);

— метода измерения (как измерять?);

— средств измерения (чем измерять?);

— достоверности измерения (с какой точностью измерять?);

— имеющихся ресурсов (какой ценой измерять?).

Существенно, что ответы на эти вопросы должны быть получены до

начала эксперимента.

1.5. РЕЗЮМЕ

1. В основе любой теории лежит некоторая исходная модель объек-

та, с изучением которого она имеет дело. С обоснования такой модели

начинается рассмотрение проблем теории .информации, теории связи,

теории оптимальной фильтрации [20—45]. Не составляет в этом отно-

шении исключения и теория точности измерительных систем, объектом

изучения которой является процесс измерения (измерительный экспери-

мент). Исходная модель теории точности измерительных систем должна,

с одной стороны, учитывать достаточно полную совокупность факторов,

оказывающих влияние на процесс измерения, и их взаимодействие,

с другой стороны, допускать ее описание с помощью адекватного мате-

матического аппарата. Более того, будучи одним из разделов киберне-

тики, эта теория должна иметь органическую связь с теми разделами

кибернетики, которые посвящены вопросам получения, преобразования

и обработки информации. Попытка обоснования подобной модели и была

предпрнята в этой главе.

2. Модель (см. рис. 1.6), отражающая специфику измерительного

эксперимента, позволяет учесть:

— вероятностную природу исследуемого объекта (ВМ

);

— статистический характер наблюдения (ВМ~);

— наличие неконтролируемых возмущений (ВМ

);

— необходимость, наряду с экземпляром ИС, рассматривать тип

ИС данного назначения (ВМ

);

— погрешность, возникающую в системе передачи размера единицы

физической величины от эталонов к рабочим приборам, а также несо-

вершенство используемой теории (ВМй);

— возможность измерения произвольных характеристик исследуе-

мого объекта (А

);

— несовершенство технических решений, принимаемых при реали-

зации ИС(и), в частности, из-за наличия ограничений (ср);

— необходимость контроля (оценки качества) ИС и типа ИС (Л

);

— цель измерения.

В дальнейшем эта модель будет несколько расширена в направле-

нии учета процессов создания и эксплуатации ИС-

Математическим аппаратом, адекватным задачам теории точности,

служат, в первую очередь, теория множеств и функциональный анализ,

а также теория случайных процессов и математическая статистика.

В приведенной модели процесса измерения легко усматриваются

основные элементы моделей, используемых в теории информации,

теории связи, оптимальной фильтрации и др., что позволяет обеспечить

необходимую преемственность как по отношению к методологическим

принципам, методам и результатам современной технической кибернети-

ки, так и по отношению к классическим концепциям метрологии.

3. Содержание развиваемой в этой книге теории точности РТС

заключается в количественном описании указанной модели, позволяю-

щем установить взаимосвязь влияющих факторов и рассмотреть на

этой основе задачи оценки погрешности, ее анализа, оптимизации ИС и

типов ИС.

Глава 2

ТЕЗАУРУС

К числу основных проблем метрологии [1] относятся определение

единиц физических величии и построение рациональной системы этих

единиц. В тех случаях (см. § 1.2), когда задача измерения связана

с получением математической модели исследуемого объекта, наряду

с единицами физических величин, необходимо рассматривать множество

матемэтических моделей, а наряду с задачей построения рациональной

системы единиц —задачу систематизации (классификации) моделей

с целью обеспечения удобства поиска небходимой модели. Обсуждение

этих вопросов и составляет основное содержание данной главы. Приве-

денный материал можно рассматривать в качестве «заготовки», исполь-

зуемой в последующих главах для выявления структуры результата

нзхмерений, описания измерительных систем, влияющих факторов и

т. д. — короче, всех элементов, входящих в основную модель процесса

измерения (см. рис. 1.6), а в пределах данной главы — как описание

структуры множеств X, М, Э и действия ВМ

Полезно обратить внимание на единство признаков для процессов

и систем, а также на связь между детерминистскими и вероятностными

моделями.

2.1. ПРИНЦИП ОРГАНИЗАЦИИ ТЕЗАУРУСА

Рассмотрим вначале задачу классификации в общей постановке.

Пусть М={т} — полное множество (так называемый универсум

задачи) рассматриваемых элементов т, вообще говоря, произвольной

природы.

Классификацией (или конечным разбиением) множества М

называется конечное семейство {М

..., М

} непустых попарно непере-

секающихся подмножеств МгФ0, М^М,

= 1, Ь множества М, з объ-

единении дающих все М:

В этом случае на М определено отношение эквивалентности (1.24).

Подмножества Мг называются классами эквивалентности (разбие-

ния). Выделение классов производится с учетом характеристиче-

ских свойств элементов т, так что (см. § 1.2)

ЦМ1 = М,

М; п м, = 0, 1ф\, уь /е={ТГ~Ц•

(2.1)

(2.2)

Мг = {т:т имеет свойство г}, г=1, Ь.

(2.3)

Предполагается, что каждый данный элемент т обязательно обладает

каким-либо одним свойством и не обладает другими. Если перенуме-

ровать каким-либо образом эти свойства, можно получить классифика-

цию, содержащую классы от 1 до Ь включительно.

Характеристические свойства можно разделить на качественные и

количественные.

Качественные свойства, которые будем называть призна-

ками, характеризуются тем, что в отношении их можно высказать лишь

суждения типа «да-нет», т. е. каждый элемент либо обладает данным

признаком, либо не обладает им (примеры: классификация К. Линнея

биологических объектов, уни-

версальная десятичная класси-

фикация— УДК).

Количественные свой-

ства, которые будем называть

параметрами, характери-

зуются числовыми значениями

(примеры: возраст человека,

число страниц книги). Заме-

тим, что если область значений параметра разбить на конечное число

неперекрывающихся интервалов, сплошь заполняющих ее, то получим

предыдущий случай (примеры: разбиение населения на возрастные

группы, выделение «параметрических рядов» приборов по охватываемым

ими диапазонам [см. (1.23)]).

Если классы выделять в соответствии с признаками, то элементы

т, входящие в класс М^, будут отличаться значениями параметров а^,

соответствующими этому' классу, и классы будут представлять собой

параметрические семейства (множества) функций

Мг = {т:т={г(х, а*), (2.4)

где /<(•) — некоторая функция аргумента х, зависящая от параметра

а*, причем х, эц могут быть как скалярными, так и векторными вели-

чинами. Предполагая, что каждый элемент характеризуется лишь

одним признаком, запишем

М = {т:т=^(х, а*), *еЕ{ТД}, а^Ль}- (2.5)

Упорядоченный набор признаков I определяет «список» классов,

образующий простейший вид классификации (рис. 2.1). Поиск нужного

элемента в такой классификации производится, по-существу, методом

перебора с числом попыток, не превышающим Ь—1 вариантов, посколь-

ку (в силу предположения о полноте классификации) последнее Ь-е

решение принимается автоматически. Примерами могут служить клас-

сификации: одиночных импульсов (прямоугольный, экспоненциальный,

пилообразный, колоколообразный, косинус-квадратный), одномерных

распределений (гауссово, пуассоновское, равномерное, релеевское).

В каждом из этих случаев класс задается видом соответствующе?

функции [{(•), а элементы класса — фиксированными значениями па-

раметров этой функции. Таким образом, здесь используется лишь один

признак.

В действительности, классы чаще всего характеризуются несколь-

кими признаками, перечисляемыми в определенном порядке, причем

каждый признак может иметь несколько «значений» (именно по такому

Рис. 2.1. Организация тезауруса «спнскоглг.

ш-п

принципу построены классификация

биологических объектов и система

УДК)

•

Рассмотрим структуру класси-

фикации, получающуюся в этом случае.

Пусть параметрическое множество

(2.4) характеризуется некоторым упо-

рядоченным набором

= {ь,..., из

ц. признаков 1^=1,^), каждый из

которых, в свою очередь, может иметь

значения (1),...,^ (п

) (призна-

ки можно в этом случае трак-

товать как составляющие —КОМПО-

Рис

2.2. Иерархическая структура

нентного вектора I). Фиксируя зна- тезауруса,

чения г'*,, V первых признаков

и оставляя значения |"

у+1

, ...,

остальных признаков „свободными", полу-

Ц V

...

чим совокупность 2 П

классов

> связанных между собой иерархиче-

х = 1

ской структурой, т. е. имеющую вид „дерева классов" (рис. 2.2). Таким

образом, имеется ц уровней иерархии с классами на г-м уровне

*=1

= 1, [а), причем каждому классу на г-м уровне подчинено классов

и- .

на у-|-1-м уровне, так что = 9бозначим|через М\

(у)-Й

класс на г-м уровне иерархии, подчиненный 1)-му классу на V—1-м

уровне (Цг) = 1, п

, —1) = 1. (см. рис. 2.2). Тогда для различ-

ных уровней будем иметь

ДМ = АЦь,..., у,

М«

=М(Р

, и,

.^ =М(1:\ I

(V)

* ' V У + 1'

V-

(2.6)

где знак А обозначает понятие «равно по определению».

Очевидны следующие свойства данной классификации:

1. Система классов полна, поскольку объединение всех классов на

любом г-м уровне равно М (ср. с (2.1))

I = !

«V—] "» «V—!

и и <<7»= и

I (V—1)=1 I (V) =

(

' ( («-1) =

1 ;

(2.7)