Розенберг В.Я. Введение в теорию точности измерительных систем
Подождите немного. Документ загружается.


При р=
1
условие (3.112) есть условие абсолютной интегрируемости
Н/(*)И1= / |/(х)|Лс<оо, (3.1113)
при р=2 — условие интегрируемости в квадрате
11/(*)11
2
2= / \}(х)Чх<оо (3.114)
и т. д., при р= оо — условие ограниченности по модулю
И/ (*)11оо =
Иш
II? (*)11Р = шах |Г (х)| = А<С. со. (3.115)
р-* ОО X
Соответствующие функционалы в (3.112) суть площадь, «энергия» и пиковое зна-
чение обобщенного импульса.
Легко заметить, что большинство характеристик сигналов и цепей, представляю-
щих практический интерес в радиоизмерениях, в силу ряда физических или математи-
ческих ограничений охватываются понятием «обобщенный импульс» (табл. 3.6). За-
метим также, что на выходе последователь-
ных анализаторов функции х) получаются
в виде функций времени }({), т. е. дей-
ствительно в виде импульсов.
„ „ ,„ „ , Таким образом, понятие «обобщенный
Рис. 3.16. Схема измерения функциона-
„„ импульс» является синонимом широкого
ла интенсивности. *
г
класса характеристик сигналов и цепей, об-
ладающих некоторыми общими математи-
ческими свойствами, что позволяет применять к ним общий математический аппарат
и получать алгоритмы обработки, инвариантные к конкретному физическому содержа-
нию функции [(х), обеспечивая тем самым унификацию аппаратуры. В тех случаях,
когда некоторая функция 1|)(х) не отвечает условию (3.112), например, не является
абсолютно интегрируемой (таковы фазочастотная характеристика, некоторые виды
вольт-амперных и переходных характеристик цепей), в качестве обобщенного импульса
можно рассматривать функцию
!(х)=й
к
^(х)/ах" (3.116)
при условии
, ач (х)
л*" <
со
)' (
ЗЛ17
>
Вместо (3.111) можно также использовать функционалы вида
11/(*)11р,
ш
='Г/ \1{х)\гт(х)4хУ/Р, (3.118)
где т (х)—весовая функция. В частности, если го(х) =6(х—х
0
), то
[/ |ЯХ)|'6(Х-Х
0
)^]
1
/Р=|/(ХО)|. (3.119)
Схема измерения функционала интенсивности в соответствии с определением
(3.111), имеет вид рис. 3.16. Нелинейный безынерционный элемент с четной характе-
ристикой вида у= |х|р обеспечивает возведение импульсов |/"(01 в степень р. Инте-
гратор дает значение интеграла от |/(0|
р
за время Т. Если входной сигнал имеет вид
периодической последовательности импульсов с постоянным периодом, то интегратор
можно выполнить в виде фильтра низких частот, обеспечивающего выделение посто-
янной составляющей
т
у = у- ^ 1/(01" «И, (3.120)
о
100
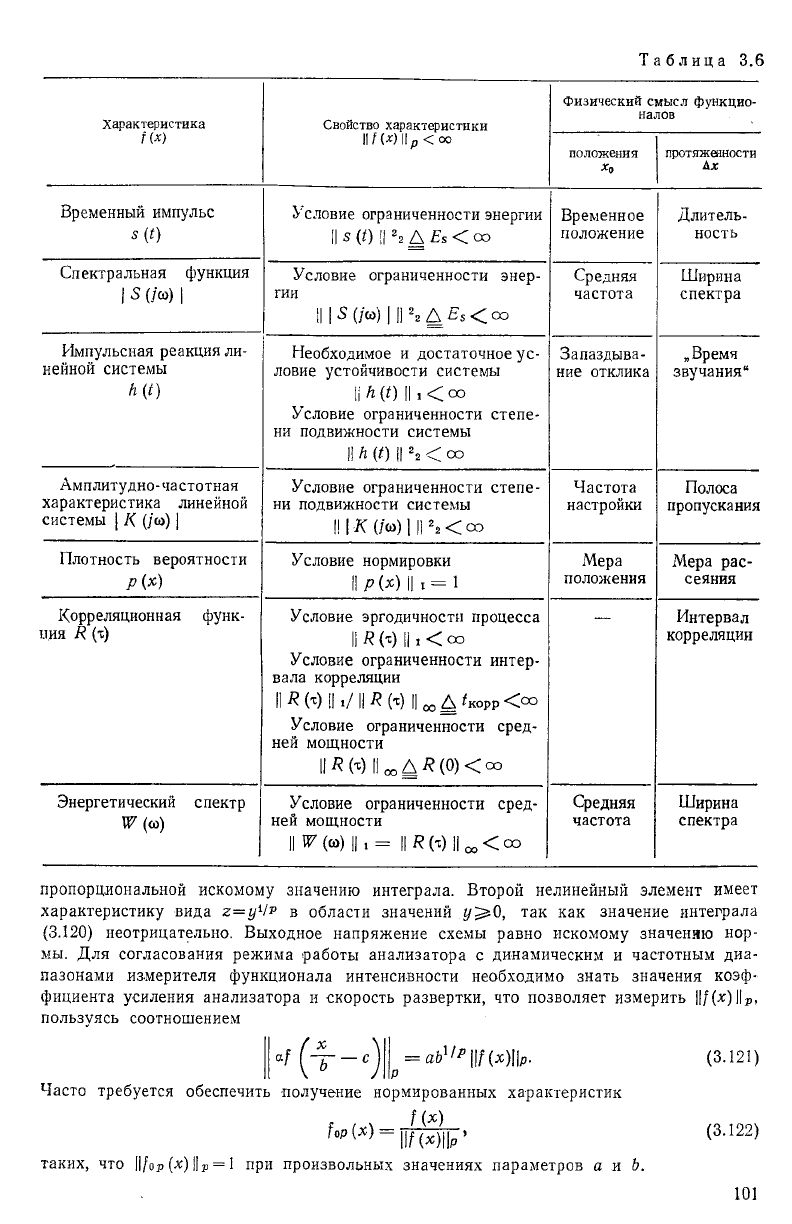
Таблица 3.6
Характеристика
Свойство характеристики
Физический смысл функцио-
налов
Пх) П/МПрСоо
положения
Хо
протяженности
Ах
Временный импульс
5(0
Условие ограниченности энергии
II 5(0 II
2
2Л&<СО
Временное
положение
Длитель-
ность
Спектральная функция
I
5 (/со) |
Условие ограниченности энер-
гии
II
1
5 (/со) |||
!
г
ДЕ
5
< со
Средняя
частота
Ширина
спектра
Импульсная реакция ли-
нейной системы
МО
Необходимое и достаточное ус-
ловие устойчивости системы
II Л
(0 II
1
< со
Условие ограниченности степе-
ни подвижности системы
II А
(0 ||
2
2
< со
Запаздыва-
ние отклика
„Время
звучания"
Амплитудно-частотная
характеристика линейной
системы | К (/ю) |
Условие ограниченности степе-
ни подвижности системы
|| |
К (/со) | || < со
Частота
настройки
Полоса
пропускания
Плотность вероятности
р{%)
Условие нормировки
II
Р(х)
||
, = 1
Мера
положения
Мера рас-
сеяния
Корреляционная функ-
ция Я (х)
Условие эргодичности процесса
II
Л (х) || , < оо
Условие ограниченности интер-
вала корреляции
II Я (т) ||,/ II Я (х) || ^ Д ^корр <оо
Условие ограниченности сред-
ней мощности
II Я СО
1!
оо А * (0)<оо
Интервал
корреляции
Энергетический спектр
Г (со)
Условие ограниченности сред-
ней мощности
||Г(со)||
1=
||«(т)||
00
<оо
Средняя
частота
Ширина
спектра
пропорциональной искомому значению интеграла. Второй нелинейный элемент имеет
характеристику вида г=у
1
/р в области значений у^0, так как значение интеграла
(3.120) неотрицательно. Выходное напряжение схемы равно искомому значению нор-
мы. Для согласования режима работы анализатора с динамическим и частотным диа-
пазонами измерителя функционала интенсивности необходимо знать значения коэф-
фициента усиления анализатора и скорость развертки, что позволяет измерить II/(ж)
II
р,
пользуясь соотношением
Часто требуется обеспечить получение нормированных характеристик
г
°
р{х
>-\\1(х)\\
Р
'
таких, что \\[о
Р
(х) ||р =
1
при произвольных значениях параметров а и 6.
(3.121)
(3.122)
101

лш
Н23ЧХ1
-и-г Т
Т
»*
2
^И
4-
ж:
•II/II;
±Г
Рис. 3.17. Структурная схема
устройства нормировки:
1 — последовательный анализатор; 2 —
усилитель с регулируемым усилением;
3 — блок управления усилением; 4 —
вычислитель нормы; 5 — блок сравне-
ния; 6 — блок выдачи опорного уровня.
Структурная схема устройства нормировки
приведена на рис. 3.17. Периодическая последо-
вательность импульсов вида (3.77) из блока 1 по-
ступает через усилитель 2 на блок 4 вычисления
нормы. Постоянное напряжение величины ||/11р,
получаемое на выходе этого блока, сравнивается
далее с опорным напряжением, вырабатываемым
блоком 6 и принимаемым за единицу. Сигнал рас-
согласования ||/1| р—1 поступает в блок 3 управ-
ления усилением, воздействуя на него таким обра-
зом, чтобы НЛ1р—1=0, т. е. НЛ1р — 1.
В соответствии с формулой (3.121) выходной
сигнал при этом будет иметь вид
00
т. е. каждый импульс последовательности будет удовлетворять условию нормировки
при любых значениях параметров Л и Г развертки.
Функционалы положения 1108 ... 110, 111].
Рассмотрим некоторые методы определения функционалов положения.
1. Метод выбранных точек основан на использовании соотношения (З.Г19) х
0
=
= аг§ / |/(х) |6(х—хц)йх, где
Хо
— значение функпионала положения, которое выби-
рается исходя из требований «устойчивости» определения по отношению к небольшим
вариациям формы обобщенного импульса. В соответствии с этим требованием исполь-
зуются способы фиксации положения импульса:
— по положению максимума (3.115)
Хо = аг§ шах (х)|;
X
• по точкам наибольшей крутизны
Хо = аг§ шах
-по положению одного из фронтов
(3.123)
#(х)
йх
Хо = аг$2 пип (х)| — кА],
(3.124)
где
С (*) 1 Г
=
\
х:
-гг>°/
или
ах
О
< к = сопз* < 1; А = тах (х)|;
а
Ш< о\;
— по положению обоих фронтов например, как среднее арифметическое;
— по положению центра симметрии и т. п.
Очевидно, что все эти способы обладают следующим свойством
Р4.1(х+с)]=Щ(х)]+с.
(3.125)
Кроме задачи фиксации положения одного импульса (по отношению к некото-
рому значению аргумента х, принятому за начало отсчета), часто возникает задача
определения разности функционалов положения двух импульсов. Так, часто оказы-
вается необходимым определить временной сдвиг между двумя импульсами (задержка,
опережение). Эта задача сводится обычно к нахождению разности функционалов по-
ложения х
с
=х"а—х'о, одинаковым образом определенных для каждого из импульсов,
102
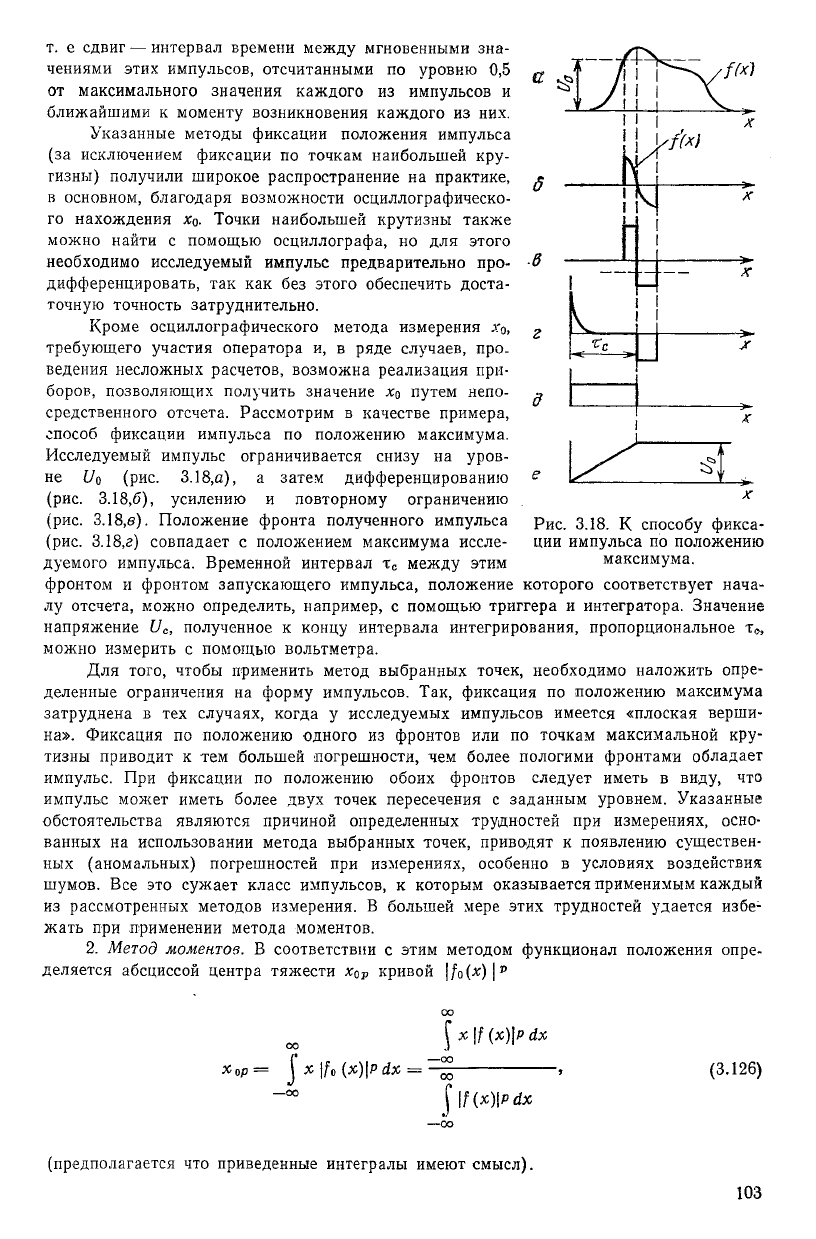
с
•В
т. е сдвиг — интервал времени между мгновенными зна-
чениями этих импульсов, отсчитанными по уровню 0,5
от максимального значения каждого из импульсов и
ближайшими к моменту возникновения каждого из них.
Указанные методы фиксации положения импульса
(за исключением фиксации по точкам наибольшей кру-
тизны) получили широкое распространение на практике,
в основном, благодаря возможности осциллографическо-
го нахождения х
0
. Точки наибольшей крутизны также
можно найти с помощью осциллографа, но для этого
необходимо исследуемый импульс предварительно про-
дифференцировать, так как без этого обеспечить доста-
точную точность затруднительно.
Кроме осциллографического метода измерения х
0
,
требующего участия оператора и, в ряде случаев, про-
ведения несложных расчетов, возможна реализация при-
боров, позволяющих получить значение х
0
путем непо-
средственного отсчета. Рассмотрим в качестве примера,
способ фиксации импульса по положению максимума.
Исследуемый импульс ограничивается снизу на уров-
не 1!
0
(рис. 3.18,а), а затем дифференцированию
(рис. 3.18,6), усилению и повторному ограничению .
х
(рис. 3.18,в). Положение фронта полученного импульса р
ис
318. К способу фикса-
(рис. 3.18,г) совпадает с положением максимума иссле- ции импульса по положению
дуемого импульса. Временной интервал т
0
между этим максимума,
фронтом и фронтом запускающего импульса, положение которого соответствует нача-
лу отсчета, можно определить, например, с помощью триггера и интегратора. Значение
напряжение И
с
, полученное к концу интервала интегрирования, пропорциональное т
с
,
можно измерить с помощью вольтметра.
Для того, чтобы применить метод выбранных точек, необходимо наложить опре-
деленные ограничения на форму импульсов. Так, фиксация по положению максимума
затруднена в тех случаях, когда у исследуемых импульсов имеется «плоская верши-
на». Фиксация по положению одного из фронтов или по точкам максимальной кру-
тизны приводит к тем большей погрешности, чем более пологими фронтами обладает
импульс. При фиксации по положению обоих фронтов следует иметь в виду, что
импульс может иметь более двух точек пересечения с заданным уровнем. Указанные
обстоятельства являются причиной определенных трудностей при измерениях, осно-
ванных на использовании метода выбранных точек, приводят к появлению существен-
ных (аномальных) погрешностей при измерениях, особенно в условиях воздействия
шумов. Все это сужает класс импульсов, к которым оказывается применимым каждый
из рассмотренных методов измерения. В большей мере этих трудностей удается избе-
жать при применении метода моментов.
2. Метод моментов. В соответствии с этим методом функционал положения опре-
деляется абсциссой центра тяжести х
ОР
кривой |/о(*)|
р
' о р
= |х|/о(*)1 РЛх = '
Лх
[|/(х)| Рйх
(3.126)
(предполагается что приведенные интегралы имеют смысл).
103

В частности, при р= 1
00
{*!/ (х)| Л*
= — (3-127)
||/(х)|<*х
—оо
— .центр тяжести по площади"; при р = 2
00
Хо2 = (3 128)
[\{(х)\*ах
—00
— «центр тяжести по энергии» и т. д.
Легко убедиться, что размерность хо
р
совпадает с размерностью х при любых р.
Рассмотрим класс функций /(х) либо четных, либо нечетных относительно центра
симметрии х. Это означает, что } (х—х) = /(х—х)—для четных функций;
/(х — х) = —}(х — х)—для нечетных функций. Отсюда следует, что функция
|/(х)|Р четна относительно х как в случае четных, так и в случае нечетных /(х). Тогда
для / (х — х)
00
I X (х)| Рйх
—ОО .
Хор— -1"Х.
^ I/ (х)|р ах
—00
Знаменатель дроби не равен нулю. Числитель равен нулю, так как он представ-
ляет собой интеграл в симметричных пределах от нечетной функции. Таким образом
Хо
Р
=х, т. е. функционал положения совпадает с абсциссой центра симметрии при лю-
бых значениях р. Если функция }(х) не является четной или нечетной, то при р\фр2
Х
Орх $
Х
0р
2
-
Если /(х) задана аналитически, то можно найти зависимость х
ор
(р). Например,
если }(х)=&~
х
, хе(0, оо), то Хо
Р
= 1/р, т. е. при р=Л х
ор
='1; при р—>оо х
йР
—>-0.
Пусть функционал положения функции [(х) есть х'
0р
. Тогда для функции
о/((х/6—с)) функционал положения
Хор=Ь(х'ор+с). (3.129)
Таким образом, при Ь=
1
х'
0р
получает приращение, равное с при любом значении а.
Отсутствие зависимости от а является, очевидно, следствием нормировки /(х) в ис-
ходном определении (3.78).
Перейдем к рассмотрению алгоритма измерения функционала положения. Пере-
пишем выражение (3.126) в виде
^ (х— х'ор)
®
(х) йх = 0, (3.130)
где ф(х) Д|/о(х) |
3
', и предположим, что мы располагаем импульсом /о(х), полученным
с помощью соответствующего анализатора (3.77). Тогда структурная схема измерителя
104
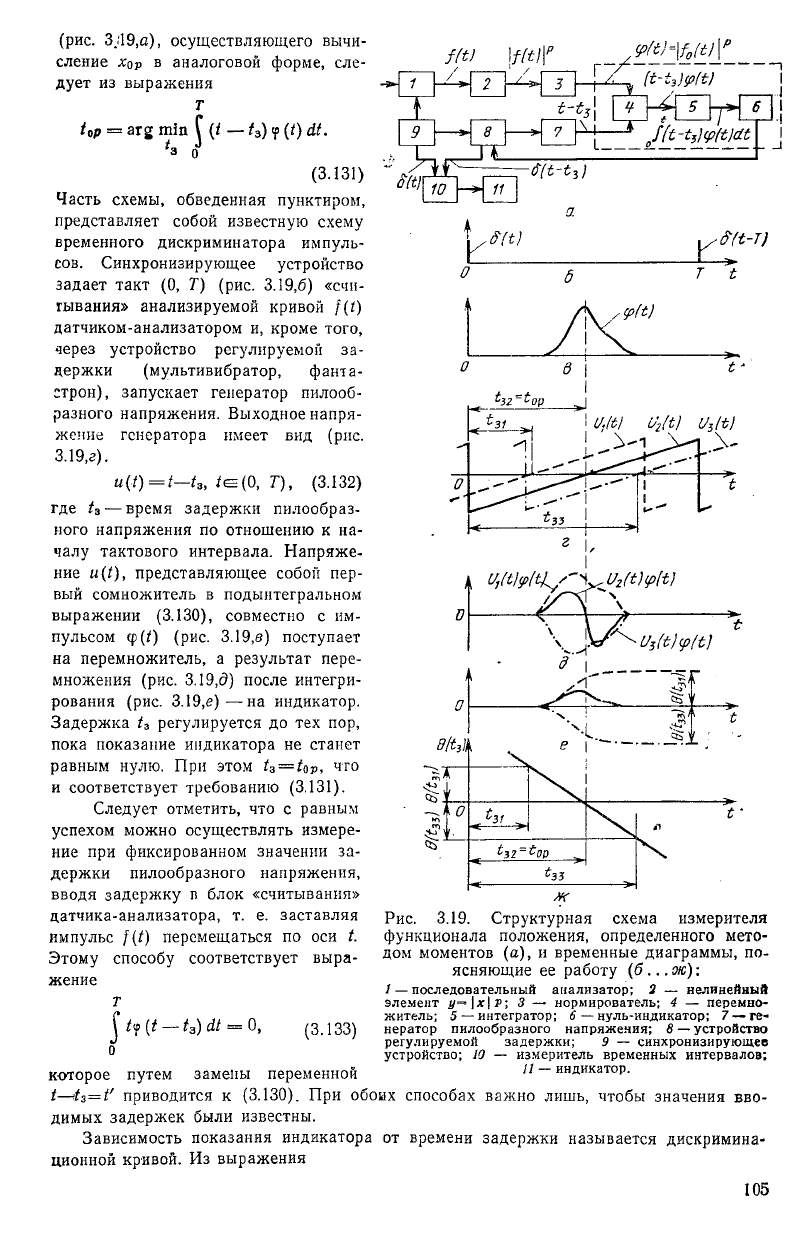
(рис. 3.119,а), осуществляющего вычи-
сление Хор в аналоговой форме, сле-
дует из выражения
т
<
0
р = аг2 ш!п \ (I — (
3
) у (/)
'з о
1
(3.131)
Часть схемы, обведенная пунктиром,
представляет собой известную схему
временного дискриминатора импуль-
сов. Синхронизирующее устройство
задает такт (О, Т) (рис. 3.19,6) «счи-
тывания» анализируемой кривой 1(1)
датчиком-анализатором и, кроме того,
через устройство регулируемой за-
держки (мультивибратор, фанта-
етрон), запускает генератор пилооб-
разного напряжения. Выходное напря-
жение генератора имеет вид (рис.
3.19,г).
иЦ)={—(
3
, *е=(0, Г), (3.132)
где и — время задержки пилообраз-
ного напряжения по отношению к на-
чалу тактового интервала. Напряже-
ние и(/), представляющее собой пер-
вый сомножитель в подынтегральном
выражении (3.130), совместно с им-
пульсом <р(/) (рис. 3.19,б) поступает
на перемножитель, а результат пере-
множения (рис. 3.19,6) после интегри-
рования (рис. 3.19,е)—на индикатор.
Задержка 1
3
регулируется до тех пор,
пока показание индикатора не станет
равным нулю. При этом и=ир, что
и соответствует требованию (3.131).
Следует отметить, что с равным
успехом можно осуществлять измере-
ние при фиксированном значении за-
держки пилообразного напряжения,
вводя задержку в блок «считывания»
датчика-анализатора, т. е. заставляя
импульс }({) перемещаться по оси I.
Этому способу соответствует выра-
жение
Т
=
(
з.133)
о
/
/
Ш\
р
1
1 /
Г"
/31
Ш1Г
1
(г-^)ф)
4
10
V.
ш
г
ж
Рис. 3.19. Структурная схема измерителя
функционала положения, определенного мето-
дом моментов (а), и временные диаграммы, по-
ясняющие ее работу (б... ж):
1 — последовательный анализатор; 2 — нелинейный
элемент у—\х\р-, 3 — нормирователь; 4 — перемно-
житель; 5 — интегратор; 6 — нуль-индикатор; 7 —ге-
нератор пилообразного напряжения; 8 — устройство
регулируемой задержки; 9 — синхронизирующее
устройство; 10 — измеритель временных интервалов;
И — индикатор.
которое путем замены переменной
I—<1
г
=1' приводится к (3.130). При обоих способах важно лишь, чтобы значения вво-
димых задержек были известны.
Зависимость показания индикатора от времени задержки называется дискримина-
ционной кривой. Из выражения
105

т
в ({„) «= | (* — * а) 7 (()
<и
= и
Р
- и (злз4)
О
следует, что в данном случае дискриминационная кривая в достаточно большой окре-
стности точки *
0
р имеет линейный характер (рис. 3.19,ж). Множитель (I—1
3
) в подынте-
гральном выражении (3.134) можно рассматривать как некоторую скользящую весовую
функцию. Возможно применение также весовых функций с{1—иного вида, напри-
мер, прямоугольных импульсов, длительность которых соизмерима с длительностью
исследуемого импульса; пары коротких импульсов, отстоящих на фиксированный ин-
тервал друг от друга; функций вида зщп (I—/о) и др.
Алгоритм измерения во всех этих случаях имеет вид
т
/*> = аг2ппп Гс(* —*з)<р(*)Л- (3.135)
'» о
Структурная схема измерителя, построенного в соответствии с (3.135), отличается от
представленной на рис. ЗЛ9,а тем, что вместо пилообразного напряжения в ней выра-
батывается напряжение, имеющее форму требуемой весовой функции. Дискриминаци-
онные кривые яри этом будут иметь форму более сложную, чем на рис. 3,'19,эл;, зави-
<1
..у
«* ,
х
г
л I аь
—
Рис. 3.20. К определению функционала протяженности методом сечений:
а —при отсчете от максимума: б — при отсчете от «плоской части».
сящую как от вида весовой функции с((), так и от формы исследуемого импульса
}({). Обычно к дискриминационной кривой предъявляются требования достаточно
большой протяженности участка ее монотонного изменения и большой крутизны в об-
ласти нуля. Первое требование обеспечивает устойчивость работы дискриминаторов,
в особенности, работающих в режиме автоматического слежения (мала вероятность
срыва), а второе — высокую точность отсчета значения функционала положения.
Функционалы протяженности.
1. Метод выбранных точек. Будем различать три разновидности метода:
— определение протяженности по условному уровню .(сечению), составляющему
заданную часть от максимального уровня («метод сечений»);
— определение протяженности по точкам, в которых характеристика обращается
в- нуль («метод нулей» и «метод первых нулей»);
— определение протяженности по условным границам, в пределах которых значе-
ние функционала интенсивности составляет заданную часть от полного значения («ме-
тод условных границ»),
а. Метод сечений. Используется определение, имеющее вид
Дх= |Х1—х
г
\ : \?(Х1,2) |— кА=0, (3.136)
где 0<&<1 —условная константа.
Границы применимости метода определяются, очевидно, требованиями существо-
вания не более чем двух решений уравнения |/(х)|—кА= 0 и условием /(х)е/,«>
(т. е. Л<оо) и являются, таким образом, довольно жесткими.
106

С=/7 = С0ГТ5{
-н
Рис. 3.21. Схема измерения
функционала протяженно-
сти методом сечений:
/ — последовательный анализа-
тор; 2 — пиковый вольтметр;
3 —триггер Шмидта; 4 — изме-
ритель временных интервалов.
Например, распределение синусоиды со случайной фазой не удовлетворяет второ-
му допущению, а частотная характеристика системы из двух связанных колебатель-
ных контуров при связи больше критической и при к^0,707 — первому. Тем не менее
данное определение имеет широкое практическое применение благодаря своей простоте
и возможности нахождения Ах непосредственно по графику или осциллограмме функ-
ции 1(х) (рис. 3.20,а).
Функционал протяженности (3.136) применяется
в качестве определения полосы пропускания избиратель-
ных систем (обычно по уровню 0,707Л), ширины диа-
граммы направленности антенн (по уровню половинной
мощности), длительности временных импульсов (поуров-
ню 0,5 А), интервала корреляции случайных процессов
(по уровню 0,01 А). В некоторых случаях, однако, пред-
почитают определять Дх в долях не от максимального
значения А, а от некоторого значения 1(х*), выбирае-
мого более или менее произвольным образом. Например,
при определении длительности временного импульса,
имеющего выброс, отсчет длительности часто производят
по уровню 0,5 Vо, где Vо — уровень, соответствующий
«плоской части» импульса (рис. 3.20,6), которая в этом
случае должна быть четко выражена.
Структурная схема измерителя, работающего по
методу сечений, приведена на рис. 3.21. Поступающие от
датчика-анализатора 1 импульсы вида (3.77) должны
иметь стандартное значение Л = сопз{, обеспечиваемое
соответствующей нормировкой и контролируемое пико-
вым вольтметром 2. Одновременно эти импульсы пода-
ются на триггер Шмидта 3, срабатывающий при дости-
жении напряжением и(() уровня кА, задаваемого дели-
телем Ди В.2, На выходе триггера образуется периоди-
ческая последовательность прямоугольных импульсов
постоянной амплитуды и длительности А1, соответ-
ствующей выбранному значению кА. Длительность этих
импульсов измеряется с помощью измерителя времен-
ных интервалов 4.
б. Метод нулей. Для финитных функций функцио
нал Ах определяется в виде
ДА-
= тедХ=|а
в
—а
н
|, (3.137)
6 /
ъА №
Г '
Ах/2^
X
Рис. 3.22. К определению
функционала протяженно-
сти:
я — методом нулей; б — по пер-
вым нулям; в — методом услов-
ных границ.
где символом тед X обозначена мера множества X; а
в
,
Чи — границы интервала (рис. 3.22,а). Для функций, при-
нимающих нулевые значения на множестве меры нуль,
Ах определяется как разность двух «нулевых» значений
аргумента, ближайших к х
0
, т. е. «по первым нулям» (рис. 3.22,6). Очевидно, что при-
менимость обоих вариантов метода весьма ограничена.
Как и в методе сечений, значение функционала протяженности в данном случае
легко найти с помощью графика или осциллограммы функции /(х). Инструментальное
измерение можно осуществить путем формирования прямоугольных импульсов стан-
дартной амплитуды и длительности, соответствующей (в определенном масштабе)
измеряемому интервалу. Например, в схеме, использующей метод нулей, прямоуголь-
ные импульсы формируются путем усиления и последующего глубокого ограничения
исследуемых импульсов или с помощью триггера Шмидта с нулевым порогом сраба-
тывания.
7

в. Метод условных границ определяется выражением
Дх =аг§ тт
ДА-', Х\
л'о+Д.е
^ Цор (х)[Р йх
•
х*о + Ьх*
| \\ор(х)\Рйх—к,
(3.138)
где 0<6<1 — условная константа (например, /г=0,95).
Для симметричных функций, полагая (без потери общности) Хо=0, получим
(рис. 3.22,а)
} №
р йх
IX:
||/(х)|Р йх
(3.139)
При р=, 1 получим протяженность «по частичной площади», при р=2 — «по ча-
стичной энергии» и т. д.
Функционал 1—к, где к — определяется на основании (3.438) или (3.139), можно
назвать коэффициентом внеполосности.
Рассматриваемый метод применим к функциям, интегрируемым в степени р, т. е.
является более универсальным, чем предыдущие, но, в отличие от ранее рассмотренных
определений, функционал (3.139) нельзя измерить непосредственно по осциллограмме,
так как необходимо выполнить сложные виды об-
работки }(х) (возведение в степень р, интегриро-
вание).
Аппаратурная реализация этого алгоритма
не вызывает существенных затруднений (рис. 3.23).
Периодическая последовательность исследуемых
импульсов (3.77) проходит через нелинейный эле-
мент с характеристикой у— |х|
р
, а затем интегри-
руется в пределах периода Г. Протяженность анализируемого участка и значение пара-
метра с должны быть такими, чтобы обеспечивалось интегрирование всего импульса. Ин-
дикатором может служить вольтметр среднего значения, показание которого, как извест-
но, пропорционально значению интеграла. Регулируя параметр с, добиваются совпадения
оси симметрии импульса с серединой анализируемого участка. Регулируя параметр а,
устанавливают показание вольтметра на первое отсчетное деление, например, на ко-
нец шкалы. Затем, меняя ширину анализируемого участка в сторону уменьшения, что
Таблица 3.7
Рис. 3.23. Схема измерения
функционала протяженности
методом условных границ.
Их)
Уз Ь
Хр
при р
Их)
1 2
3 4
5
М*)
о
0,71о
0,58а
0,5а
0,45а
Гр (*)
0,86 г 0,74г
0,71г
0,68г
0,67г
1п (х)
1
Гз
1
КЗ
1
Кз
1
КЗ
1
V 3
Ы*)
А
0,5Л
0,33 А
0,25.4 0,2,4
108
соответствует изменению предела интегрирования в формуле (3.139), следует устано-
вить показание вольтметра на второе отсчетное деление, соответствующее к-й доле
от первоначального. Значение ширины анализируемого участка, полученное при этом
будет (в соответствующем масштабе) равно искомому Ах. При реализации алгоритма
(3.138) необходимо, кроме того, отыскивать экстремум функции двух переменных.
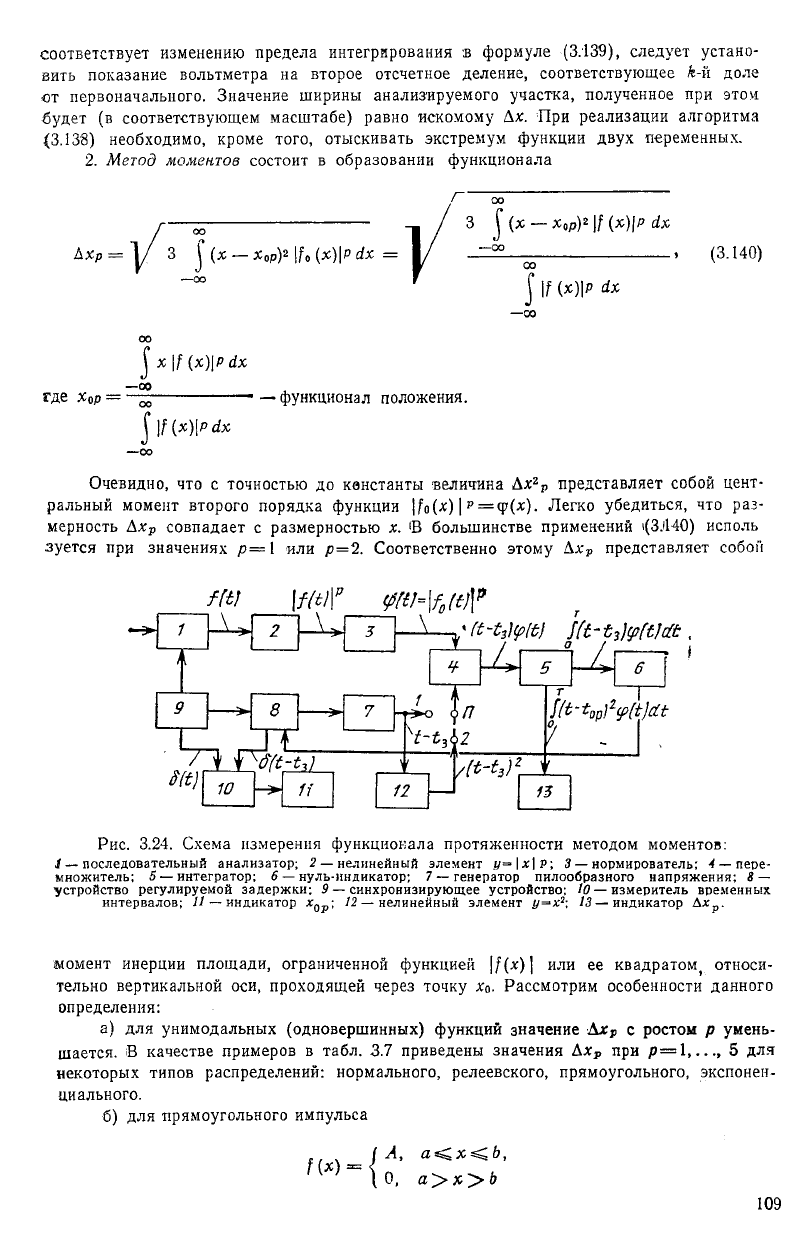
2. Метод моментов состоит в образовании функционала
АХр=|/
Л
3 ^ (х — х
0
р)
2
=
| (х — Хор)
2
[Х)\Р йх
(3.140)
р йх
где Хор
:
00
|х|/(х)|
Рйх
—00
00
|| !(х)\Рйх
—00
— функционал положения.
Очевидно, что с точностью до квнстанты величина Ах
2
р
представляет собой цент-
ральный момент второго порядка функции |/о(х) |
Р
= (р(х). Легко убедиться, что раз-
мерность Ах
р
совпадает с размерностью х. В большинстве применений |(ЗЛ40) исполь
зуется при значениях р —
1
или р=2. Соответственно этому Ах
р
представляет собой
ЯП
\№\
р
Ш)
10
н
•
а-ь
3
)ср1ь} Нь-
1— / ° / ,
/ 1 /
^ 5 -А-
9
8
7
9
8
7
Кь-Чр^срМм
V - I
12
13
Рис. 3.24. Схема измерения функционала протяженности методом моментов:
Л
— последовательный анализатор; 2— нелинейный элемент у=-\х\р; 3— нормирователь; 4— пере-
множитель; 5 — интегратор; 6 — нуль-индикатор; 7— генератор пилообразного напряжения; В —
устройство регулируемой задержки; 9— синхронизирующее устройство; Ю— измеритель временных
интервалов; Л — индикатор х
0
;
12
— нелинейный элемент у=х
2
-,
13
— индикатор Ах
момент инерции площади, ограниченной функцией |/(х)] или ее квадратом
)
относи-
тельно вертикальной оси, проходящей через точку х
0
. Рассмотрим особенности данного
определения:
а) для унимодальных (одновершинных) функций значение Ах
р
с ростом р умень-
шается. В качестве примеров в табл. 3.7 приведены значения Ах
р
при р=1,..., 5 для
некоторых типов распределений: нормального, релеевского, прямоугольного, экспонен-
циального.
б) для прямоугольного импульса
I А, а<х< 6,
ПХ)
= \0, а>х>Ь
109
