Розенберг В.Я. Введение в теорию точности измерительных систем

Подождите немного. Документ загружается.

При частотной модуляции (ЧМ)

*чм(0 = Л С08 [«,( + 5

Д2 ^ + (3.188)

причем закон ЧМ имеет вид

со

(0 =

«РР

(О /М = Шо+ДсоЕо (0, (3.189)

где (?)—полная фаза; Д<о = 5

Д2; — эффективная девиация частоты.

При использовании '(3.174), (ЗЯ75), (3.177), (ЗД78) в случае детерминированных,

сигналов мы получаем соответственно известные [84] определения девиации частоты

и коэффициента модуляции.

3. Принятый сигнал ц(/)=Л

у(/).

За счет искажающего действия канала р.(I) отличается от \{1). Часто считают,,

что эти искажения приводят лишь к изменению закона модуляции, так что

|х(г) =Л

-г(0 =«(?, а,, ..., щ-

хШ]> а„), (3.190)

где функция х(-). вообще говоря, не совпадает с функцией ф(-)- Однако, согласно-

принятому нами допущению, мы не будем учитывать этого обстоятельства и предпо-

ложим, что оператор детектирования выбирается согласно (3.162).

4. Выходной сигнал т)(/) =Л

|л(/).

Покажем на примерах |(в целях иллюстрации концепции «синтеза по определе-

нию»), что получающиеся при таком подходе алгоритмы приводят к широко применяе-

мым на практике схемным решениям 112... 14]. Заметим, что известные руководства

по основам радиотехники, излагающие способы детектирования, в гораздо большей сте-

пени аппелируют к эвристическим соображениям, чем это необходимо при использова-

нии указанной концепции.

А. Амплитудное детектирование.

Решая уравнение (3.185) относительно А(1), получим

А(()=у АмОзесшо*. (3.19!)

Согласно (3.162) это выражение представляет собой искомый алгоритм ампли-

тудного детектирования. Однако он нереализуем из-за наличия бесконечных разрывов,

которые претерпевает функция 5ес соо^ в точках я(26 + 1)/2 (к— целое число). Чтобы

обойти это затруднение, найдем приближенные реализуемые алгоритмы. С этой целью

заменим в (3.191) «нереализуемую» функцию зес Юо( «реализуемой» функцией

достаточно близкой к зес а>о(, но не имеющей разрывов. При этом

(3-192)

где О(-) —некоторый дополнительный оператор;

а) пусть

(зесо^ *е={*: 1

ес«.< |< Л*};

Ь'И$12п (зес со„Г),

|зес <о

г | > М}.

Подобная функция получается при двухстороннем ограничении функции

вес <Оо( на уровнях ±М (Л1=сопз1<оо). Появляющиеся при этом «провалы», харак-

терные для процесса амплитудного детектирования, можно, как обычно, сгладить при

помощи соответствующим образом подобранного линейного фильтра, реализующего

оператор 0( •);

б) полагая в (3.193) М= 1, получим

120

?(*) =51дп(5ес ШоО =51дп Л

Ам (0-

(3.194)

при этом

^ЛМ(ОШ) =^АМ(*) 5

'§п ГАМ (О = IVАм (/) I

и после фильтрации

м*) = (3.195)

где к (I) —импульсная реакция фильтра.

Последнее выражение описывает работу классической схемы двухтактного линей-

ного амплитудного детектора;

в) если положить

?(/) =51^0)0^, (3.196)

то (с учетом фильтрации) получим алгоритм

А(1)= | м

АМ

(т) 51Нсо

тк (1-х) Л, (3.197)

описывающий процесс синхронного детектирования.

В условиях отсутствия модулирующего сигнала рассматриваемые алгоритмы

описывают работу, например, детекторных вольтметров переменного тока [14]. В со-

четании с алгоритмами измерения функционалов протяженности, описанными в пре-

дыдущем примере, они приводят к широко известным схемам модулометров, основан-

ных на методе «двойного детектирования» [12 ... 14].

Б. Частотное детектирование

Положим для упрощения записи в (3.188) А0= 1,

фо

= я/2 и перепишем это вы-

ражение в виде

чм

(0 = 5^пФ(0, (4.198)

где Ч

(0—полная фаза. Формально дифференцируя (ЗЛ98) и решая полученное урав-

нение относительно (№/а1, получим закон частотной модуляции (3.189) в виде

, ЙФ (О Л

цм

(()

<о({) = —±±= (3.199)

аг аг

По аналогии с (3.195) запишем

®(0'

к(1 — т)йт. (3.200)

йг

Таким образом, колебание вначале необходимо подвергнуть высокоча-

стотному дифференцированию '(например, с помощью колебательного контура), в ре-

зультате чего оно приобретает характер АМ-ЧМ сигнала, закон АМ которого воспро-

изводит функцию а затем — обычному амплитудному детектированию и сглажи-

ванию. Как известно, именно на этом принципе основана работа частотных дискрими-

наторов. Подвергая сигнал <в(/) повторному детектированию с целью измерения

функционала протяженности (например, по алгоритму (3.181)), приходим к обычной

схеме девнометра [12 ... 14].

Рассмотрим теперь измерение функционалов, связанных с модулированными сиг-

налами. Используя полученные операторы (3.195), (3.197), (3.200) детектирования

сигнала представленного выражением (3.190), мы выделим сигнал Т](0. прибли-

зительно воспроизводящий функцию х[б(0]- Д

ля

этого сигнала точно так же, как и

для сигналов §(<) и а((/), можно получить (измерить) значения функционалов поло-

жения и протяженности его характеристик. Сравнивая их с соответствующими вели-

чинами для сигналов и V(/), можно судить о некоторых свойствах канала и

модулятора — динамическом и частотном диапазонах, характере искажений.

Весь комплекс измерений, о которых здесь идет речь, при использовании приве-

денных алгоритмов можно обеспечить при наличии сравнительно небольшой номенкла-

121

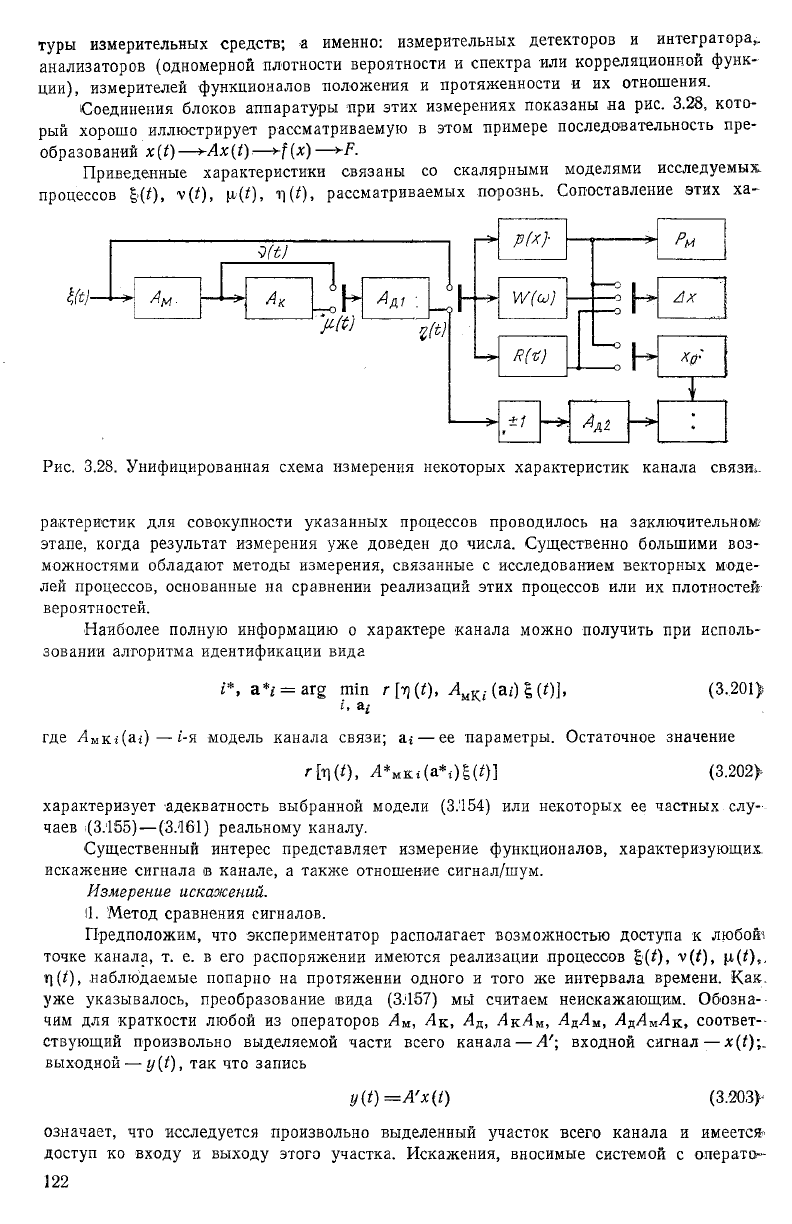
туры измерительных средств; а именно: измерительных детекторов и интегратора,,

анализаторов (одномерной плотности вероятности и спектра или корреляционной функ-

ции), измерителей функционалов положения и протяженности и их отношения.

Соединения блоков аппаратуры при этих измерениях показаны на рис. 3.28, кото-

рый хорошо иллюстрирует рассматриваемую в этом примере последовательность пре-

образований х(1)——>-{(х)—ур.

Приведенные характеристики связаны со скалярными моделями исследуемых

процессов КО.

ц(0>

1(0. рассматриваемых порознь. Сопоставление этих ха-

Рис. 3.28. Унифицированная схема измерения некоторых характеристик канала связь.

рактеристик для совокупности указанных процессов проводилось на заключительно»

этапе, когда результат измерения уже доведен до числа. Существенно большими воз-

можностями обладают методы измерения, связанные с исследованием векторных моде-

лей процессов, основанные на сравнении реализаций этих процессов или их плотностей

вероятностей.

Наиболее полную информацию о характере канала можно получить при исполь-

зовании алгоритма идентификации вида

»•, а*« = аг

шш г [т) (0, Л

мК(

.(а/Ш0]. (3.201)

где Ашкг(аг)—1-я модель канала связи; т — ее параметры. Остаточное значение

'[•ПСО, Л*мКг(а*г)К0] (3.202)

характеризует адекватность выбранной модели (3.154) или некоторых ее частных слу-

чаев >(3.155)—(3.161) реальному каналу.

Существенный интерес представляет измерение функционалов, характеризующих,

искажение сигнала в канале, а также отношение сигнал/шум.

Измерение искажений.

1. Метод сравнения сигналов.

Предположим, что экспериментатор располагает возможностью доступа к любой?

точке канала, т. е. в его распоряжении имеются реализации процессов КО. ^(0>

т)(0> наблюдаемые попарно на протяжении одного и того же интервала времени. Как.

уже указывалось, преобразование вида (3.157) мы считаем неискажающим. Обозна-

чим для краткости любой из операторов А

, А к, Л

, ЛкЛ

, Л

Л к, соответ-

ствующий произвольно выделяемой части всего канала — Л'; входной сигнал — х(0;.

выходной'—у(0, так что запись

у({)=А'х({) (3.203)-

означает, что исследуется произвольно выделенный участок всего канала и имеете»'

доступ ко входу и выходу этого участка. Искажения, вносимые системой с операт»--

122

ром А', можно определить (с учетом сделанного предположения о неискажающей си-

стеме) выражением [118]

К = пип М (р [у

(а, с, (), у

(/)]} =

а, с

= т!п Г Г р [ах {1-е) — у

(0] р [х ((), у

(/)] йх {I) йу

({), (3.204)

а, с * «

-где

у„(а, с, I) =А

(а, с)х(() =ах((—с) (3.205)

— неискаженный сигнал (А

(а, с)—идеальный оператор (3.167)); р(г)—некоторая

неотрицательная неубывающая функция \г\, обращающаяся в нуль при 2=0 (функ-

ция потерь).

Таким образом

М{р{у*{а, с, (), </

'(01} (3.206)

представляет собой средний риск [31]. Заметим, что интегрирование в (3.204), вообще

говоря, континуальное, так что г/

(0]— совместный функционал вероятности

искаженного (3.203) и неискаженного (3.205) сигналов. В случае взаимно-эргодических

процессов ((3.204) можно записать в виде

К = пип Пт -=г\^[ах(1 — с)—уо{Щй1. (3.207)

а, с Т-*оо ' ,)

К = т1п Нт -4- Г [ах (1-е) — у

(О]

й( (3.208)

а, с

Г->оо

ш, таким образом, величина К представляет собой просто среднюю мощность сигнала

ошибки

Ау{()=а*х{(—с*)—у

({), (3.209)

еде а*х((—с*)—идеальный сигнал, наиболее близкий к реальному сигналу у(()

в смысле среднеквадратического критерия приближения.

Очевидно, что выражение |(3.208) можно использовать также для оценки иска-

жений детерминированного сигнала. -Пусть, например,

Ук(() =А 51П (<0<+ф),

УР о = 2 +

1=1

•что соответствует прохождению гармонического сигнала через нелинейную систему

(3.160). Допустим, что в сигнале у

(() первая гармоника имеет наибольшую амплиту-

ду. Оценим искажения сигнала по среднеквадратическому критерию. Тогда с учетом

ортогональности гармоник будем иметь

ГГ 00 "12 00

4-Д Л81пН +

)-^Л

зШ(но +

-) й1 = "• / 4" 5]

ари А*=А

ф*

= ф!.

Отношение К к эффективному значению Л1/|/"2 первой гармоники

А\

(=2

2,0

123

известно в радиотехнике под названием коэффициента гармоник (коэффициента не-

линейных искажений, клирфактора). Более общее выражение (3.207) позволяет опре-

делить аналогичную величину для произвольной формы детерминированного сигнала,

для произвольного случайного сигнала и системы и для произвольного критерия.

2. Метод сравнения законов распределения.

Предыдущий метод, давая исчерпывающее представление об искажениях в ка-

нале, обладает той особенностью, что для его использования на входы измерительной

системы необходимо одновременно подавать процессы со входа и выхода исследуемого

канала. Во многих случаях (при исследовании прохождения сигнала через устройство

небольших размеров) реализация этого метода не связана со сколько-нибудь суще-

ственными затруднениями. Однако в некоторых приложениях, как, например, при

исследовании каналов связи значительной протяженности, его применить не удается.

В этих случаях можно сравнивать не непосредственно входной и выходной процессы,

а их характеристики с учетом их изменения в идеальной системе ['119].

'Пусть, например, канал представляет собой нелинейную искажающую систему

(3.160), в то время как идеальная система по-прежнему описывается оператором!

(3.157). Определим нелинейные искажения путем сравнения одномерных плотностей

вероятностей входного сигнала х{1) (с учетом преобразования (3.157)) и выходного

сигнала у((). Соответствующие одномерные плотности вероятностей этих сигналов

имеют вид, аналогичный (ЗЛ67) и (3.165), а величина искажений определяется выра-

жением (ср. с (3.204))

(3.211)

Используя в качестве критерия сравнения р(-,') расстояние по вариации (3.24),

получим

йх.

(3.212)

Для корреляционного критерия (3.27)

— тах

шал

Для энтропийного критерия (3.34)

— ехр {гшп [—АН (а, с)]},

а, с

где, согласно (3.32)

АН (а, с) — Н [р

(х)] — Н

1 /х-с\

и при всех а и с распределение р

( —-— 1

1 /х — с\ -

подчиняется условию (3.31)

(3.213)

(3.214)

(3.215)

(3.216)

Если характеристика 1|)(г) линейна, величины К^ , Кн, Кн обращаются в нуль.

При наличии нелинейности они возрастают, не превышая, однако, единицы. Таким

образом, эти величина можно использовать в качестве коэффициентов нелинейности

канала.

124.

Значение а=а*, обеспечивающее экстремум в выражении (3.211) и его частных

случаях (3:212) ... (3.214), имеет смысл коэффициента усиления в данном режиме.

Пользуясь этим методом, можно производить поиск оптимального режима, выбирая

такое значение с=с* на характеристике ч|>(2), при котором искажения минимальны

(выбор «рабочей точки»). Этот метод можно также с успехом использовать в случаях,

когда идеальная характеристика не прямолинейна, а имеет вид, например, квадратич-

ной параболы или кривой, описываемой уравнением более зысокого порядка. В этом

случае можно отыскать путем вариации некоторого параметра (параметров) участок

реальной характеристики, на протяжении которого она менее всего уклоняется от за-

данной функциональной зависимости. Кроме того, метод пригоден для оценки искаже-

ний, возникающих при модуляции и детектировании. В этом случае необходимо ис-

пользовать неискажающий (измерительный) детектор, с выхода которого сигнал

подается на анализатор плотности вероятности.

Примеры расчетов, основанных на применении энтропийного критерия, приве-

дены в работе {119]. При оценке линейных искажений аналогичным образом сравни-

ваются корреляционные функции или энергетические спектры.

Измерение отношения сигнал/шум [120].

Допустим, что два независимых стационарных случайных процесса \(() и

каждый из которых зависит от одного параметра, образуют аддитивную смесь (3.155).

Априори предполагаются известными одномерные плотности распределения вероятно-

стей и Р°

{х) соответственно процессов го(0 и По(0 с единичными пара-

метрами.

Процесс образуется в результате смешения \'({) и гь{1) в неизвестной про-

порции, определяемой отношением

= а

/а„. (3.217)

так что

(0 = л,*« (0 \

п (() = а

п„ (I) )'

(3.218)

Параметр <7 имеет смысл отношения сигнал/шум, если, например, считать сигна-

лом, а п(() —шумом.

Одномерное распределение р^ (х) процесса найдется как свертка

Зная суммарное распределение р^ (х), необходимо найти отношение сигнал/шум и пара-

метры <7, я

, а

распределений д, (х) и р

(х). Возможен ряд методов решения этой за-

дачи, для применения которых необходимо, чтобы, по крайней мере, один из процес-

сов, входящих в смесь, имел негауссово распределение, так как в противном случае

распределение композиции гауссово для любых значений параметра 17.

1. Метод сравнения законов распределения '(энтропийный критерий).

Воспользуемся для решения задачи выражениями (3.30)—(3.32). Энтропия сум-

марного распределения имеет вид

^ = -5/>,Л*)1пА1 (*)<**• (

220

В качестве экстремального распределения возьмем распределение ро(х) с учетом

линейного преобразования

= (3.221)

125.

тде а

— параметр экстремального распределения. Общее ограничение, накладываемое

на распределение композиции, можно записать в виде (3.31)

— р^

(х) 1п

(х) Лх = Я

тде

(3.222)

(3.223)

(3.224)

=— I Рз(х) 1п р

(х) Лх.

Используя (3.017), (3.219)—(3.223), получим

= \

= !г(я) I

С учетом наложенных ограничений (3.222), используя (3.224), найдем разность

энтропии суммарного и экстремального распределений:

ДЯ(

) = Яэ-Я

Величина ЛЯ служит мерой отличия суммарного распределения от экстремального.

Более удобным для практического пользования является энтропийный коэффициент

подобия (3.33)

=ехр(—ДЯ), (3.226)

который является функцией от ц |(рис. 3.29). Схема, изображенная на рис. 3.30, позво-

ляет получить значение Л*н, после чего искомое значение д* определяется по графику.

А'

Рис. 3.29. Графическое решение за-

дачи (Л*п—экспериментально най-

денное значение коэффициента подо-

бия; <7* — соответствующее отноше-

ние сигнал/шум).

Рис. 3.30. Схема, реализующая соотношение

(3.225).

(Композиция Рр (х) экспоненциального и равномерного распределений для разных

д показана на рис. 3.31. Если в качестве экстремального выбрать распределение, от-

личающееся от одного из распределений, образующих композицию, то кривая Л(д)

получается немонотонной, что приводит к неоднозначности результата измерения

•(рис. 3.32).

2. Метод моментов.

Данный метод можно реализовать, используя теоремы сложения математических

ожиданий и дисперсий независимых случайных процессов, образующих аддитивную

смесь:

М, + М

= М 1

О.+ 0,-0,

)•

226)

где М

и М

— функции а„; В^ и В

— функции Решая систему уравнений (3.226)

с двумя неизвестными, находим параметры распределений а, и а

126

В тех случаях, когда математические ожидания равны нулю, необходимо исполь-

зовать центральные моменты более высокого порядка. Например, форму суммарного

распределения р^ (х), которая зависит от того, в каких соотношениях входят и

({) в [А(0, т. е. от д, можно характеризовать с помощью коэффициентов асиммет--

рии и эксцесса уг (рис. 3.33)

| (х - М

у р^ (х) йх

~ [| (х-ЛЬ)»/^*)^]

Уг =

(х — м

)*Рр (х)ах

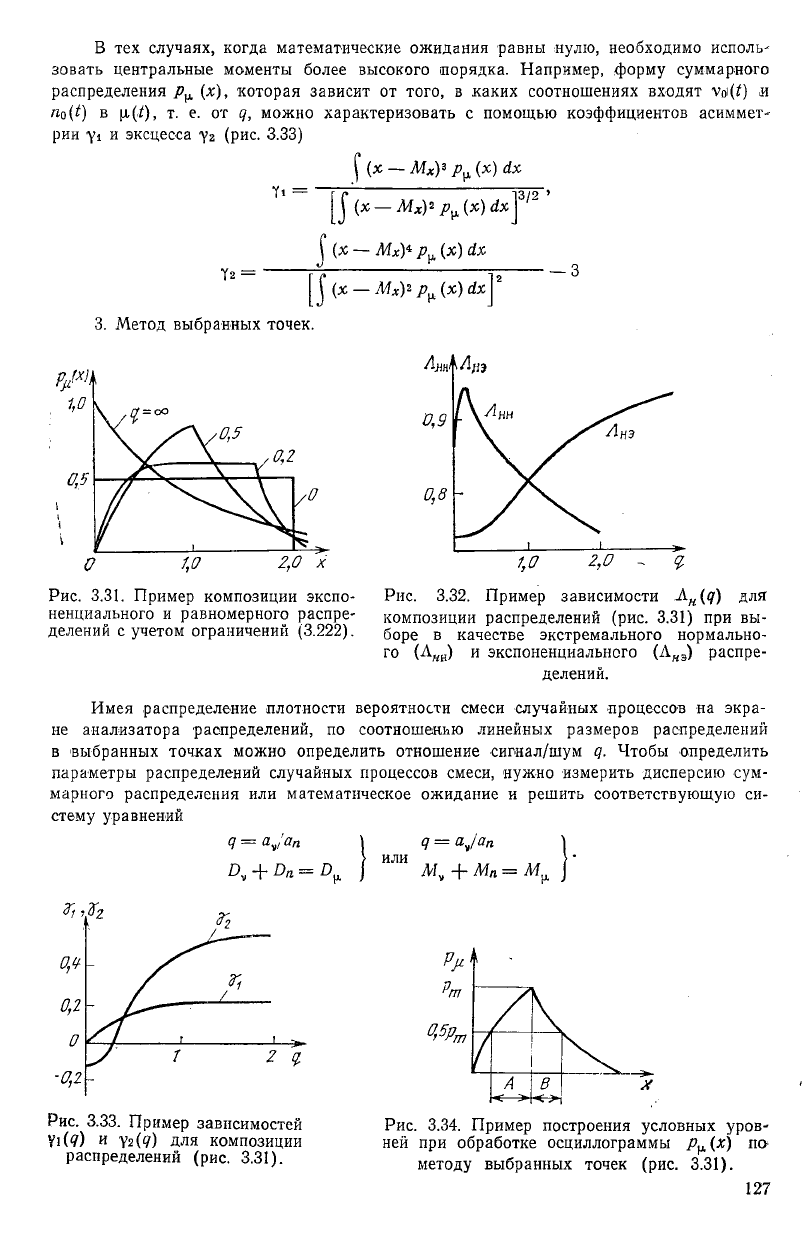
3. Метод выбранных точек.

/у (*)

<*х

1,0

2,0 х

1,0

г,о „

Рис. 3.31. Пример композиции экспо-

ненциального и равномерного распре-

делений с учетом ограничений (3.222).

Рис. 3.32. Пример зависимости А

(</) для

композиции распределений (рис. 3.31) при вы-

боре в качестве экстремального нормально-

го (Л

нн

) и экспоненциального (Л

нэ

) распре-

делений.

Имея распределение плотности вероятности смеси случайных процессов на экра-

не анализатора распределений, по соотношению линейных размеров распределений

в выбранных точках можно определить отношение сигнал/шум д. Чтобы определить

параметры распределений случайных процессов смеси, нужно измерить дисперсию сум-

марного распределения или математическое ожидание и решить соответствующую си-

стему уравнений

д = а^ап ) д = а^'а

= о

или

М,+Мп=М

Рис. 3.33. Пример зависимостей

VI(<7) и у

(д) для композиции

распределений (рис. 3.31).

Рис. 3.34. Пример построения условных уров-

ней при обработке осциллограммы р^ (х) по

методу выбранных точек (рис. 3.31).

127.

На рис. 3.34 и 3.35 показаны соответственно пример построения условных уров-

ней и получающаяся при этом зависимость отношения В/А от ц.

Можно отметить следующие особенности изложенных методов:

— метод измерения, основанный на использовании энтропийного критерия по

сравнению с известным методом максимального правдоподобия, применяемым в радио-

локации для решения аналогичных задач, обладает следующими преимуществами:

универсальностью и простотой применения в случае негауссовых процессов. К недо-

статкам следует отнести то, что в методе используются лишь одномерные распреде-

ления, что приводит к потере информации;

— метод моментов довольно легко реализуется аппаратурно, но не является

универсальным, так как не всегда дает однозначное решение задачи; заметим, что

а случае энтропийного критерия неоднозначность устраняется выбором соответствую-

щего экстремального распределения (см. рис. 3.32);

— при использовании метода выбранных точек возникает необходимость в до-

полнительных построениях при обработке осциллограммы, что связано с потерей точ-

ности. Но данный метод реализуется без решающих устройств, что является его суще-

ственным достоинством. Более подробное изложение этих методов, а также примеры

расчетов можно найти в [120].

Основываясь на формальной аналогии интеграла Дюамеля (2.102) и композиции

законов распределения (3.219), аналогичный метод можно применять для измерения

параметров временных импульсоз «ли параметров линейных инерционных цепей, если

известны искаженный импульс, прошедшь'й через цепь, форма входного сигнала и фор-

ма импульсной реакции цепи. Например, кривые (см. рис. 3.31) можно рассматривать

как импульсы «а выходе интегрирующей НС-цепи, получающиеся при воздействии на

ее .вход прямоугольных импульсов.

Пример 4. «Упрощение характеристик». [103]

Рассмотрим преобразование вида

(см. рис. 3.12), необходимость которого возникает тогда, когда исходная характери-

стика М-Х'). полученная с помощью ИС, оказывается слишком сложной для того, что-

бы по ней можно было сделать какие-либо выводы, ввиду чего требуется ее опреде-

ленным образом упростить, получив характеристику [

(х) с помощью другой ИС и,

наконец, пользуясь этой характеристикой, измерить функционалы Р. 'В качестве }г(х)

будем использовать так называемую информационную характеристику [103].

В двух предыдущих разделах мы сравнивали одномерные плотности вероятно-

стей исследуемых процессов. Как уже отмечалось, исследование взаимных характери-

стик входного и выходного процессов открывает существенно большие возможности.

В качестве таких характеристик широко используются взаимные корреляционные, мо-

ментные и структурные функции, являющиеся функционалами от взаимных двумерных

плотностей вероятностей этих процессов.

В/А

Рис. 3.35. Пример зависимости

В/А (д) для композиции распределе-

ний Рр (х) (рис. 3.31).

Ш^Ш-УР

128.

Интересно также рассмотреть функционал, определенный на некотором множест-

ве {р}= элементами которого являются взаимные двумерные плотности вероятно-

стей ^ хг, т) стационарных эргодических случайных процессов §(/) и т](/),

обладающий свойствами (ср. с (1.26)):

Р(Р1, Р2)>0, р(р, р) =0;

р, р

рг^З*. ](3.227)

Представляют также интерес его нормированные значения — коэффициент .различия

(ср. с (3.12))

и коэффициент подобия (ср. с (3.14))

0^Л=1—

а также любые монотонные функции указанных величин.

>В частности, существенный интерес представляет исследование характеристик,

описывающих эволюцию двумерной плотности вероятностей случайных процессов

(в том числе, одного процесса) при изменении интервалов между отсчетами. Подобной

характеристикой является функционал

Р^, (0 = ,,(*!. хг, х), ^(х.)/>,(*.)]. (3.228)

который в силу (3.227) и стационарности процессов обладает следующими свойствами:

ч М >0; ^ , (т) = р

, (_), (3.229)

а в силу эргодичности

11т р.

(т) = 0,

где т

определяется из уравнения

шах

{') =

{1т).

Таким образом, р^ ^ (-с) характеризует зависимость между значениями | ((,) и г\ (/

)=»

=Т|(*«+т) двух стационарных процессов. Примерами таких функционалов является

расстояние по вариации |(ср. с (3,24))

~2 II1 Р\. 1

(

Хи

' ~~ Р\

(Х2) 1 =

—оо

= — Л Д, (Хг) I р

(XI [ Хг, т) — р^ (х

) | йх

йх

(3.230)

—оо

я информационная функция

оо

Л ЛХи Хг, -с)

, (

Х1

, Хг, ,) 1п Л*

**'

(3.231)

Функции ^ ^ (т) и ^ (х) обращаются в нуль, когда значения ${1) и

(< + т)

процессов независимы. ^^

г]

(г) существует для всех ^

>7]

(х 1, х

, т) в силу условия

нормировки. Напомним, что в качестве процессов §(/) и т| (() мы рассматриваем вход-

ной и выходной сигналы некоторой искажающей системы, например, канала, описы-

ваемого выражением ,(3.154).

9—96 129