Розенберг В.Я. Введение в теорию точности измерительных систем

Подождите немного. Документ загружается.

се построения модели. Поэтому невозможно написать инструкцию или

учебник по построению моделей» [62, стр. 84]. Примириться с таким за-

ключением трудно, поскольку очевидно, что от выбора модели целиком

зависит все дальнейшее поведение системы. Действительно, из неравен-

ства

Д^/Ч + Дг,.

(где г

— теоретическая погрешность (5.101); Р

— погрешность на всех

этапах последующей реализации системы) следует, что даже если

предположить =

погрешность может иметь существенную величи-

ну Р = т. е. никакие усилия на последующих этапах не приведут

к успеху, если на этапе выбора модели допущен серьезный промах.

К счастью, подавляющее большинство задач связано не с «по-

строением» модели при отсутствии какой бы то ни было априорной

информации, а с выбором предпочтительной модели из множества за-

ранее заданных моделей. В этих условиях можно ввести необходимую

формализацию и решать задачу выбора модели алгоритмическими мето-

дами.

Совершенно естественно отождествить множество заранее заданных

моделей с тезаурусом М, играющим роль «метамодели», заменяющей

объект в задаче выбора модели.

Необходимо далее дать количественную интерпретацию термину

«предпочтительная модель». С этим термином, очевидно, связаны тре-

бования «простоты» и «адекватности».

Требование простоты вытекает из того соображения что выбор

слишком сложной модели приводит к излишним затратам ресурсов на

последующих этапах проектирования, производства и эксплуатации си-

стемы; с другой стороны, при чрезмерных упрощениях модель не будет

сохранять существенные свойства объекта. Наряду с «простотой»

(«сложностью»), можно говорить о «стоимости», понимая под этим тер-

мином затраты времени, денежных средств, материалов, выражаемые

некоторым числом.

Требование адекватности отражает цель, ради достижения которой

создается система и количественно выражается значением некоторого

заранее заданного функционала, сравнивающего реальный объект с его

моделью. Роль такого функционала играет теоретическая погрешность

(5.101).

Ввиду очевидной противоречивости обоих требований, необходим

разумный компромисс между ними, выражаемый, например, требова-

ниями «максимальной адекватности при заданной сложности» или «мак-

симальной простоты при заданной адекватности», представляющими

собой канонические формулировки задач на отыскание экстремума

функционала при наличии ограничений.

В задаче выбора оптимальной модели предполагаются заданными:

1. Множество

М = {т

т=х = у

}=Уж (6.36)

«истинных» моделей — в форме (2.10) или (2.14); в последнем случае

априорное распределение р(х) (5.101) описывает действие основного

вероятностного механизма ВМ

2. Множество

{Р

} = {Р

-.М

& Р

(М) = У

} (6.37)

220.

невзаимно-однозначных детерминированных отображений множества М

«в себя», так что М

с:М (или, что то же, У&с=У), причем каждое из

таких отображений определяет некоторое множество М

= Р

(М) непол-

ных моделей (2.25), (2.120). Из множества (6.37), точнее, из его допу-

стимого подмножества, которое будет определено ниже, выбирают иско-

мое оптимальное отображение, являющееся решением задачи.

3. Функционал

г, А г, (/="*) 4 г [М, Ри ОЩ] А г (У

, Г*) =

Р [Уи

(х), у

(л)]

И йх А г и

~ (6.38)

вир

[у

(х), у к (х1] А г

— теоретическая погрешность (5.101), характеризующая адекватность

модели М

объекту. Конкретный вид функционала определяется в за-

висимости от цели измерения, влияющей на выбор критерия сравнения

р(- , •), а также от наличия или отсутствия информации о распределе-

нии р(х), в соответствии с чем либо

Г1

= п, либо

гх

= г.

4. Зависимость затрат (ресурсов, стоимости, сложности) С от выбо-

ра Ри, характеризующая последствия, к которым приводит тот или иной

выбор на дальнейших этапах реализации и эксплуатации ИС (типа

ИС), предназначенной для измерения характеристики ук{х), а также

предельно допустимое значение С

таких затрат. Это значение играет

роль ограничения, налагаемого на множество допустимых управлений

в данной задаче, поскольку искомое отображение Р*кор* выбирают те-

перь не из множества (6.37), а из его подмножества

{Рк}с = {Р

:С(Р

)^С

}. (6.39)

На основании этих данных и в соответствии с (6.35) задача выбора

оптимальной модели по критерию «максимальной адекватности при за-

данной сложности» имеет вид

Р*

=аг§ ш! г

(Р

). (6.40)

ор4

<={Гк}с

Мы пишем 1пГ вместо гшп, поскольку минимум, вообще говоря, в преде-

лах множества {Р

}

может не существовать.

Прежде чем перейти к обсуждению путей решения этой задачи,

предположим, что каждое отображение вида Р

представляет собой по-

следовательность

={РМ, Р^, ..., Р

}, VО^-ь со, (6.41)

такую, что каждый последующий член этой последовательности обра-

зуется из предыдущего путем какого-либо невзаимно-однозначного ото-

бражения Р

1)^ КкСд,, (6.42)

причем Р^ = 1 и, очевидно, Р^ = ... р

Поскольку каждое отображение Р

действует „из М в М", полу-

чаем (см. (3.240))

М = РМ (М)^Р

(Ж) (6.43)

221.

или, что то же самое,

М Э М<" Э уИ<

Э ... =Э М'"-

» Э , (6.44)

.где М'

х)

Д/^

(х)

(М).

Конкретный вид отображений Р

определяется способом организа-

ции тезауруса. Так, для принятого нами в гл. 2 способа последователь-

ность отображений {/ч,

•

•Р} соответствует последовательности при-

знаков (ограничений), добавляемых при

перемещении сверху вниз по некоторой

траектории классификационного дерева,

начиная с нулевого уровня иерархии до

л'-го включательно. Отсюда получаем по-

следовательность «вкладывающихся» друг

в друга подмножеств (6.44) (ср. с (2.29)).

Число р, в (6.41) совпадает с числом

уровней иерархии, а множество {Р} (6.37)

эквивалентно совокупности всех классов

данного тезауруса, задаваемых кодами

их адресов (2.11). Далее, внутри каждого

класса выделяется некоторая последова-

тельность отображений, которые приво-

дят к постепенному упрощению (огрубле-

нию) модели. Так, например, функциона-

лу вероятностей случайного процесса или

бесконечной последовательности конечномерных распределений соответ-

ствует Р(°\ переход от Р

к /

означает применение операции одно-

кратного интегрирования «-мерной плотности вероятности

(см. рис. 2.5);

для систем аналогичная операция соответствует отбрасыванию одного чле-

на в усеченном ряде Винера-Вольтерра (см. рис. 2.7). Аналогичная ситуа-

ция имеет место при использовании любых других характеристик

(например, определяемых математическим ожиданием некоторых

функций (2.56)), используемых при задании неполных моделей процес-

сов и систем. Соответствующие примеры приводились в § 2.2 и 2.3.

Из (6.44) следует, что

г, (М, м™) Д г, (Р

) = г, (V) < Г

(V + 1), (6.45)

т. е. последовательность {г(0)=0, п(1),

• •

пМ} является неубываю-

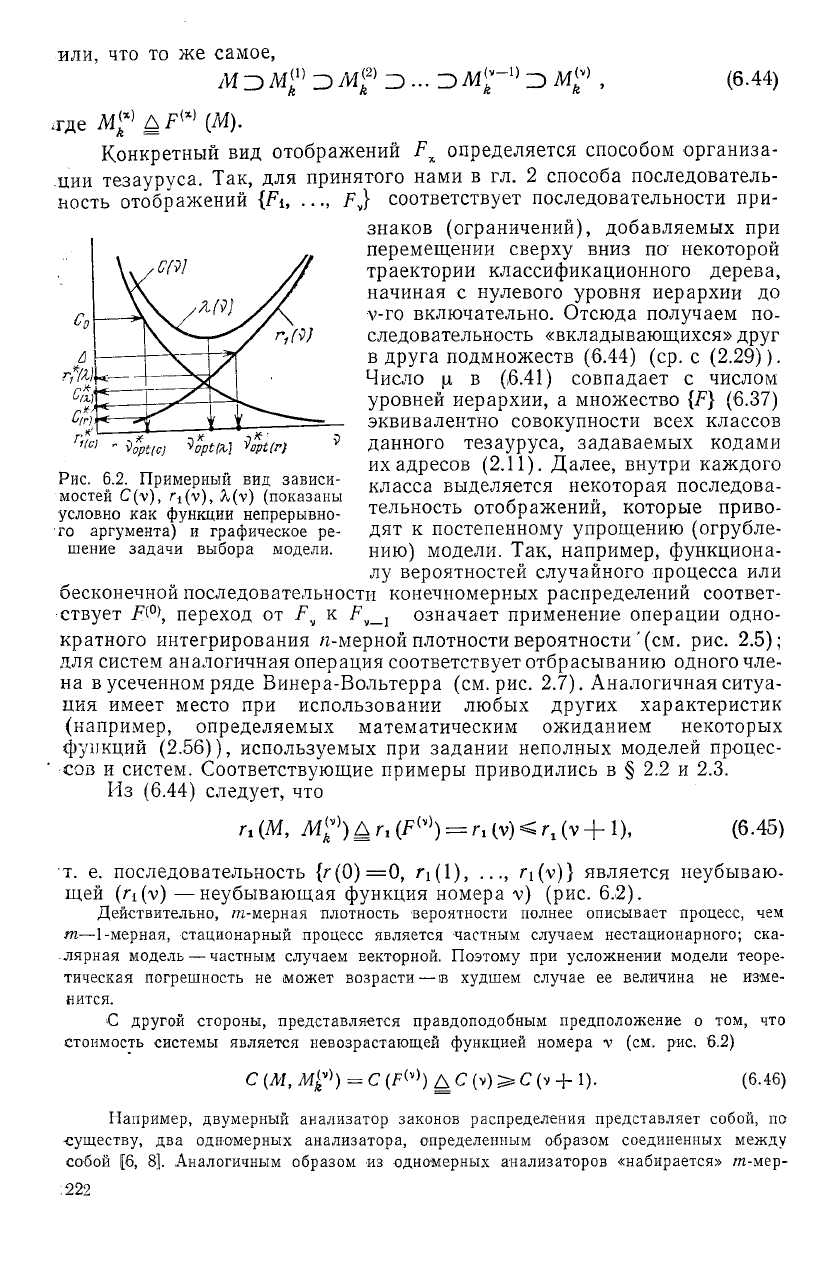
щей (/ч(г) —неубывающая функция номера V) (рис. 6.2).

Действительно, от-мерная плотность вероятности полнее описывает процесс, чем

т—1-мерная, стационарный процесс является частным случаем нестационарного; ска-

лярная модель — частным случаем векторной. Поэтому при усложнении модели теоре-

тическая погрешность не может возрасти—в худшем случае ее величина не изме-

нится.

С другой стороны, представляется правдоподобным предположение о том, что

стоимость системы является невозрастающей функцией номера V (см. рис. 6.2)

С (М, М^) = С (рМ) Д С (V) > С (V + 1). (6.46)

Например, двумерный анализатор законов распределения представляет собой, по

существу, два одномерных анализатора, определенным образом соединенных между

собой 1[6, 8]. Аналогичным образом из одномерных анализаторов «набирается» от-мер-

:222

мостей С (V), /Ч^), X(V) (показаны

условно как функции непрерывно-

го аргумента) и графическое ре-

шение задачи выбора модели.

ный. Ясно, что стоимость такого анализатора растет с ростом т. Другой пример:-

коррелометр при сдвиге т между случайными функциями х(() и х((—т), равном нулю...

превращается в дисперсиометр, но дисперсиометр, выполненный как специальный при-

бор, при прочих равных условиях дешевле коррелометра.

Из этого последнего предположения следует, что множество {Р

}с

(6.39) допустимых отображений включает в себя лишь те отображения,

которые соответствуют значениям V, при которых функция С(ч) не пре-

вышает величины С

, а из выражений (6.40) и (6.45)—что искомое

отображение Р*нор1 находится как решение уравнения

\'*ор1(с) '• С (у) = Со, (6.47)

причем из всевозможных последовательностей вида (6.41) выбирается

та, которая дает наименьшее значение л^*

ред). При этом искомые-

оптимальные отображения, модель и значение теоретической погрешно-

сти будут соответственно равны

ор4 (с)

(^ор* (С))' |

= (6-48).

г*1 (с) = г (М, М*

к(с)

Указанные данные и представляют собой результат решения зада-

чи (6.40) (см. рис. 6.2) об отыскании оптимальной модели по критерию

«максимальной адекватности при заданной сложности».

Задача об отыскании оптимальной модели, отвечающей требова-

нию «максимальной простоты при заданной адекватности», двойствен-

ная по отношению к задаче (6.40), формулируется в виде

к е {

к}г

где

{Р

}

={Р

:п(Р

)^^У, (6.50)

Д1 — заданная константа — значение неотрицательной скалярной вели-

чины, характеризующее предел допускаемой теоретической погрешности-

(6.38). Проведя рассуждения, аналогичные тем, которые были исполь-

зованы в предыдущей задаче, получим решение (ср. с (6.48))

и соответствующие ему оптимальные отображения, модель и затраты

(см. рис. 6.2)

^ к орЦг) — ^

(V*ор!

(г)У>

М*

(л) = Р*

кор( (г)

(Ж); (6.52)--

С*<п = С(Р*

кориг)

). )

Рассмотрим задачу нахождения оптимальной модели по критерию

(6.18) «взвешенной комбинации» критериев (6.40) и (6.49), имеющему

в данном случае вид

\о* =

аг

Ш1

+ (Ш (6.53)

РК 6{^}ДОП

где Х

и К

соответственно «веса» (или «значимости») функционалов

г\(Р

) и С(Р

)\ {РЙЬОП — множество всевозможных отображений, опре-

деляемое структурой тезауруса. Функция (см. (6.18))

ад=ЛгПМ+&сС(у), (6.54)

223..

значение V*

ор

(X)

, определяющее вид оптимального отображения ^*

Ао

р(

(Х)

и модели М(Р*

к ор{(Х)

), а также значения теоретической погрешности

г*,

(Х)

и затрат С* (Я), соответствующие минимуму в (6.53), показаны на

рис. 6.2.

Итак, если заданы: множество («метамодель») М (6.36) истинных

моделей, множество (6.37) всевозможных отображений, критерий

(6.38) адекватности и значение С

(6.39) допустимой стоимости, то

решение задачи (6.40) выбора оптимальной модели проводится в сле-

дующем порядке:

1) определяется совокупность {Мъ\ всевозможных моделей М

= ЫЩ\

2) эти модели ранжируются, согласно (6.43), по степени их инфор-

мативности, путем вычисления последовательности {г(М, М^)} (6.45);

3) находится последовательность значений стоимости {С(М, М^')}

16.46);

4) из этой последовательности выбирается член, соответствующий

значению стоимости, ближайшему (меньшему) к значению С

(6.47);

5) номер этого члена указывает оптимальную модель М*щ

) и соот-

ветствующее ей значение теоретической погрешности

г* 1

(С

)

(6.48).

Значение г*ц

), вообще говоря, должно быть проверено на соответ-

ствие установленным требованиям Д1, а именно:

г\ (с) <" Д» модель принимается | ^ ^

г*| (с) > Д| => модель отвергается. /

В последнем случае необходимо пересмотреть метамодель или уве-

личить значение С

Наметим ход решения ряда задач, часто встречающихся в приложениях. Основ-

ной интерес будет представлять порядок ранжирования моделей по их информатив-

ности.

Пример 1. Определение информативных составляющих слу-

чайного векторного поля. Допустим, что явление, представляющее интерес

для исследователя, оказывает то или иное влияние на поведение различных физиче-

ских полей, представляющих собой различные физические величины я|з; (1=1, п) (на-

пример, температуру, акустическое давление, скорость), зависящие от пространствен-

ных координат % и времени {. в принципе, для наиболее полного извлечения полезной

информации об этом явлении следовало бы исследовать векторное поле

1>(х. 0=

№(ОС, 0 4>»(х, 01 '(6.56)

где 0 (1=1, п) 1-я компонента, представляющая собой скалярное поле, вклю-

чающее в себя все п компонент, связанных с рассматриваемым явлением. Известно,

однако, что экспериментальное исследование векторного поля (например, с целью

обнаружения или распознавания явления, оценки параметров объекта и т. п.) пред-

ставляет собой весьма сложную задачу, для решения которой требуются большие

затраты. Поэтому важно уменьшить число исследуемых компонент, сохранив лишь

те из них, которые в наибольшей степени связаны с исследуемым явлением, и по-

жертвовав остальными (малоинформативными) компонентами, возникает вопрос о том,

какие из компонент наиболее информативны и сколько таких компонент необходимо

учесть, чтобы стоимость системы не превысила заданной величины.

224.

Итак, считаются заданными: множество полей (6.56) вместе с соответствующей

ему вероятностной мерой, т. е. тезаурус М (6.36); критерий г

(6.36); значение Со

(6.47). Множество {Рк} (6.37) можно построить, например, следующим образом: рас-

смотрим всевозможные поля вида

4>«(х. 0 = (1>1в(х.'0.-". Мг. 0). (6.57)

такие, что

^ либо ф*(Х'0;

1&{%>

0=1 , , > . т—

I либо а (х)> I = 1,

где с

(

(%)—некоторая детерминированная функция или константа, например, равная

математическому ожиданию г|),(х, 0- Эти поля получаются из поля (6.56), если раз-

личные совокупности его компонент полагать неинформативным;:, т. е. константами.

Всего, очевидно, возможно 2" видов таких полей: сюда будут входить поля, построен-

ные в предположении, что информативными являются некоторая одна компонента,

некоторые две, три и т. д. компоненты, наконец, все компоненты, т. е. исходное

поле (6.56).

Таким образом, множество {РА} есть множество всевозможных отображений

модели поля (6.56) в модель поля (6.57). Далее необходимо ранжировать полученные

этим способом модели по степени их информативности. С этой целью вычисляются

всевозможные расстояния — неотрицательные величины

(у)

=з

Жх>0. (X. 01.

а «

представляющие собой значения теоретической погрешности, соответствующие каждой

из 2" моделей и располагаемые в порядке их возрастания. Полученная последова-

тельность {г^*'} — решение задачи ранжирования моделей векторного поля по их

информативности. В качестве «рабочей» модели выбирается та, которая удовлетворяет

требованиям в отношении точности и стоимости. Одно из возможных требований

состоит в том, чтобы число информативных компонент равнялось заданному числу т.

Тогда множество возможных моделей будет равно числу сочетаний С

из п по т.

Так, если т= 1, то это требование означает, что должна рассматриваться скалярная

модель векторного поля. При этом число моделей будет равно п ив результате их

ранжирования будет выявлено, какая из комтнент векторного поля является наиболее

информативной. Очевидно, что результат ранжирования будет различным, в зависимо-

сти от выбранного критерия /ч, что вполне соответствует интуитивным представле-

ниям.

Пример 2. Определение информативных составляющих слу-

чайного векторного процесса. Эта задача решается аналогично предыду-

щей, являясь ее частным случаем. Вместо (6.56) будем иметь

ф(0 = ИМ0,---, ЧМО), (6.58)

причем компоненты (1=1, п) можно рассматривать, например, как скалярные

процессы, соответствующие тем или иным изучаемым физическим величинам г|5{ в фик-

сированных точках /* пространства.

Пример 3. Определение информативных составляющих слу-

чайного вектора. Имеется п статистически зависимых случайных величин, об-

разующих вектор

1|)=(ф1,..., г|)„). (6.59)

По условиям, связанным с ограничениями на сложность (стоимость) системы обра-

ботки, требуется делать выводы по наблюдениям некоторой совокупности т<п из этих

величин. Необходимо определить, какие именно т величин следует наблюдать. Оче-

15—96 225

видно, задачу можно рассматривать как частный случай предыдущей, когда компо-

ненты (г='1, п) не зависят от времени.

Пример 4. Определение информативных параметров. Предполо-

жим, что задана некоторая известная скалярная функция [(х, 01,..., а

)—модель

исследуемого объекта, зависящая от аргумента х и векторного параметра а =

= (а1,..., а

). Требуется использовать модель, представляющую собой некоторую

другую функцию 'ф*(х, Ь) из заданного класса, такую, что размерность вектора Ь

меньше размерности вектора а, причем потеря точности от такой замены должна

быть минимальной. Эта задача представляет собой задачу аппроксимации. Обычно

класс функций {ф(х, Ь} выбирают так, чтобы можно было решать некоторую экстре-

мальную задачу методом направленного поиска. Однако в некоторых случаях прихо-

дится прибегать к перебору.

Пусть, например, исследуемый процесс имеет вид

х(0=а

(1+|(/)) соя (со

г+ /г1(/)кЙ+фо)+п(/),

где |(0> Л(0> "(О—случайные процессы с заданными свойствами, а

, Шо, фо — неиз-

вестные параметры. Если положить значения дисперсий некоторых процессов равными

нулю, то из этой модели можно получить модели гармонического, АМ, ЧМ, АМ-ЧМ

сигналов, смесей этих сигналов с шумом. Другим примером служит модель (3.154)

канала связи и ее частные случаи '(ЗЛ55) ... (3.161).

Примерами, иллюстрирующими процесс выбора модели, могут служить также

задачи, связанные с определением оптимального набора каналов многомерного анали-

затора при заданных априорном распределении исследуемых процессов, стоимости С

{

одного -канала и предельно допустимой стоимости всего анализатора Со = С1Я, где п —

число каналов. В этом случае задача сводится к определению оптимального положе-

ния интервала анализа (см. (3.151) и рис. 3.26), при котором охватывается «наиболее

информативная» часть параметров.

6.3. ЭТАП ПРОЕКТИРОВАНИЯ. МИНИМИЗАЦИЯ

АЛГОРИТМИЧЕСКОЙ ПОГРЕШНОСТИ

Этап проектирования включает в себя решение задач «собственно»

проектирования и комплексирования.

Решив задачу «собственно» проектирования, получают

оптимальный оператор ИС (в общем случае — оператор, удовлетворяю-

щий заданным требованиям). Решение задачи комплексирования

находят в виде совокупности требований, предъявляемых к субсисте-

мам, входящим в ИС, при выполнении которых вся ИС, собранная из

таких субсистем, удовлетворяет необходимым требованиям. На основа-

нии этих требований разрабатывают (или выбирают) комплектующие

изделия при изготовлении ИС.

Рассмотрим вначале задачу «собственно» проектирования.

Согласно (6.35) и (5.119) оптимальный оператор /1*''опт определяет-

ся соотношением

аг§ шщ г

(А

хь,Ахк), (6.60)

}ДОП

где Гг{А

, Ах

)—алгоритмическая погрешность; {.4}

ДО

п — допустимое

множество операторов, из которого производится выбор Л*

оп

т, ограни-

226

ченное заданными извне требованиями; — множе-

ство исследуемых объектов, определенное на этапе выбора модели

(6.48)); ук=А

— некоторая достаточная характеристика исследуемо-

го объекта, определенная на множестве подлежащая измерению.

Таким образом, в данной задаче предполагается, что:

— реальный объект описывается некоторой моделью, заведомо

принадлежащей А^'вд. Это предположение справедливо с точностью до

полученного ранее значения г*ц

) (6.48) теоретической погрешности; на-

помним, что эта модель может быть, в частности, формальной или

структурной (см. гл.2);

— на множестве М*ц

) задано априорное распределение р(х

если задано распределение р(х) на множестве М, поскольку /^ор*

(6.48) — детерминированное отображение; напомним, что в зависимости

от того, задано это распределение или нет, выбирается вид оператора

2 (см. (4.67), (4.68) соответственно);

— одно из обязательных требований, налагаемых на класс {Л}

ДО

допускаемых операторов, состоит в том, что объем наблюдений ограни-

чен (т. е. число наблюдаемых реализацией конечно *>); описание этих

реализаций задается в виде функции правдоподобия р(хк\х:_) (см.

(4.70), (5.74)); в некоторых случаях вводится добавочное предположе-

ние о возможности продолжить наблюдение для получения дополни-

тельных данных;

— вид критерия сравнения р(- , •) должен быть выбран (см. §4.1),

исходя из назначения ИС, хотя во многих случаях этой информацией

жертвуют во имя удобства вычислений; как правило, предпочтение от-

дается среднеквадратическому критерию.

Методам нахождения оптимального алгоритма (6.60) посвящены

многочисленные публикации, к которым мы и адресуем читателя. Не-

которое представление о возможных вариантах постановки задачи оты-

скания оптимального алгоритма может дать классификация, основан-

ная на выделении совокупности признаков, вытекающих из (6.60):

1) возможных видов результата измерения (измеряемой . характе-

ристики) у

—АиХк; 2) времени наблюдения 7"; 3) априорного распре-

деления р(х); 4) критерия сравнения р(- , •); 5) модели процесса х(Ь),

1<=Т\ 6) ограничений <р(Л), налагаемых на множество {Л}доп.

Если критерий среднеквадратического отклонения отнести, напри-

мер, к одному классу, а все остальные — к другому и подразделить

ограничения, налагаемые на множество {Л}

доп

, на требования либо ли-

нейности (2.101), либо нелинейности, то даже при таком грубом раз-

биении число вариантов (рис. 6.3) равно 6х2

=192. В действительно-

сти же число вариантов много больше, поскольку, например, распреде-

ление р(х) можно задать не полностью, а, скажем, конечным числом

моментных функций; количество возможных критериев р(- ,•) неогра-

ниченно— так только в классе критериев Ь

(1.30) имеем р— 1, 2,

модели процесса х(1) могут принадлежать различным классам, число

•которых зависит от имеющегося тезауруса, развивающегося и совер-

шенствующегося с течением времени; множества {/4}

ДО

п можно опреде-

лить различными совокупностями и комбинациями ограничений вида

<гс(Л)^Г и т. д. Поэтому мы ограничимся лишь упоминанием о некото-

*> Если исследуемый процесс эргодичен по отношению к измеряемой характери-

стике, то можно использовать одну реализацию конечной длительности.

Г 5* 227

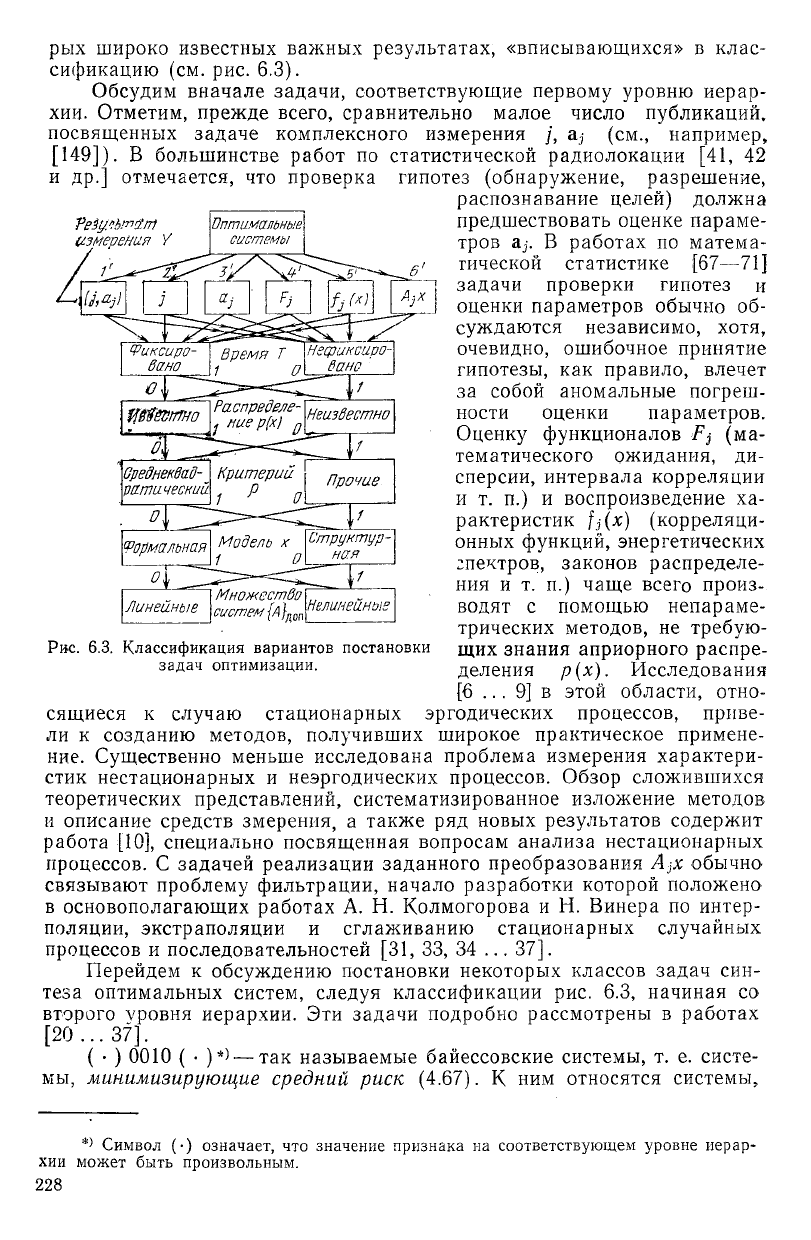
рых широко известных важных результатах, «вписывающихся» в клас-

сификацию (см. рис. 6.3).

Обсудим вначале задачи, соответствующие первому уровню иерар-

хии. Отметим, прежде всего, сравнительно малое число публикаций,

посвященных задаче комплексного измерения /, а, (см., например,

[149]). В большинстве работ по статистической радиолокации [41, 42

и др.] отмечается, что проверка гипотез (обнаружение, разрешение,

распознавание целей) должна

Результат

измерения V

предшествовать оценке параме-

тров а

;

. В работах по матема-

тической статистике [67—71]

задачи проверки гипотез и

оценки параметров обычно об-

суждаются независимо, хотя,

очевидно, ошибочное принятие

гипотезы, как правило, влечет

за собой аномальные погреш-

ности оценки параметров.

Оценку функционалов Р, (ма-

тематического ожидания, ди-

сперсии, интервала корреляции

и т. п.) и воспроизведение ха-

рактеристик (корреляци-

онных функций, энергетических

спектров, законов распределе-

ния и т. п.) чаще всего произ-

водят с помощью непараме-

трических методов, не требую-

щих знания априорного распре-

деления р(х). Исследования

[6 ... 9] в этой области, отно-

сящиеся к случаю стационарных эргодических процессов, приве-

ли к созданию методов, получивших широкое практическое примене-

ние. Существенно меньше исследована проблема измерения характери-

стик нестационарных и неэргодических процессов. Обзор сложившихся

теоретических представлений, систематизированное изложение методов

и описание средств змерения, а также ряд новых результатов содержит

работа [10], специально посвященная вопросам анализа нестационарных

процессов. С задачей реализации заданного преобразования А ,х обычно

связывают проблему фильтрации, начало разработки которой положено

в основополагающих работах А. Н. Колмогорова и Н. Винера по интер-

поляции, экстраполяции и сглаживанию стационарных случайных

процессов и последовательностей [31, 33, 34 ... 37].

Перейдем к обсуждению постановки некоторых классов задач син-

теза оптимальных систем, следуя классификации рис. 6.3, начиная со

второго уровня иерархии. Эти задачи подробно рассмотрены в работах

[20 ... 37].

(

•

) 0010 (

•

)*>•—так называемые байессовские системы, т. е. систе-

мы, минимизирующие средний риск (4.67). К ним относятся системы,

Рис. 6.3. Классификация вариантов постановки

задач оптимизации.

*' Символ (•) означает, что значение признака на соответствующем уровне иерар-

хии может быть произвольным.

228.

основанные на использовании широко известных методов — метода

отношения правдоподобия и его разновидностей (критерий Неймана—•

Пирсона, «идеального наблюдателя», «взвешенной комбинации») —

в задачах принятия решения (обнаружение, распознавание образов),

а также методов максимального правоподобия и максимума апосте-

риорной вероятности— в задачах оценки параметров. Следует заме-

тить, что предельные (потенциальные) возможности системы оценки

параметров, характеризуемые минимальной границей дисперсии, можно

установить с помощью неравенства Крамера-Рао без необходимости

отыскания оптимального алгоритма. Это позволяет оценивать качество

неоптимальных (номинальных) систем с точки зрения их близости

к оптимальным [31, 69].

Разновидностью этого метода (З'ООЮ(-)) является классический

метод наименьших квадратов.

( •) 0110 (

•

) —так называемые минимаксные системы, т. е. систе-

мы, минимизирующие максимальный условный риск (4.68). Использо-

вание этого критерия, нередко считываемого чрезмерно осторожным

(«перестраховочным»), представляется вполне оправданным для систем

широкого применения. Другим способом преодоления «априорной труд-

ности» является применение непараметрических методов принятия реше-

ния [28, 150].

(

•

) 1010 (

•

) —так называемый метод последовательного анализа,

предложенный А. Вальдом, основанный на применении «двухпорогово-

го» правила принятия решений, при котором попадание в «зону неопре-

деленности» служит сигналом для продолжения наблюдения, а также

«усеченный» вариант этого метода, при котором по истечении опреде-

ленного времени наблюдение приостанавливается и то или иное реше-

ние-принимается обязательно.

(

•

) 1110 (• ) —так называемые адаптивные (обучающиеся, накап-

ливающие опыт) системы, основанные чаще всего на использовании

метода стохастической аппроксимации (процедура Роббинса-Монро и

ее разновидности), о котором мы упоминали в § 1.2 [19, 20, 28]. В част-

ности, тот или иной выбор вида функции у* приводит к различным

методам поиска экстремума в выражении (6.60), рассматриваемом

с точки зрения задачи математического программирования (метод

градиента, метод случайного поиска и др.). При этом одним из показа-

телей качества используемого метода может служить некоторый функ-

ционал, харакеризующий быстроту сходимости к нулю значения сред-

него риска, рассматриваемого как функция объема наблюдений.

б'ООООО — так называемая задача винеровской фильтрации, приво-

дящая к интегральному уравнению Винера-Хопфа, решение которого

получают в виде импульсной реакции искомого оптимального линейного

фильтра. В последние годы уделяется внимание установлению связи

задачи фильтрации с задачами принятия решения и оценки параметров.

6'1001 (•)—так называемая задача калмановской (или «динами-

ческой») фильтрации, основанная (в отличие от задачи винеровской

фильтрации) на использовании рекуррентных алгоритмов и представле-

нии исследуемого процесса структурной моделью как процесса на

выходе формирующего фильтра, заданного дифференциальным уравне-

нием, возбуждаемого порождающим белым шумом [32, 37].

На этом мы закончим обсуждение вариантов постановки задач син-

теза оптимальных систем. Отметим лишь, что, по нашему мнению, раз-

витие и детализация классификации (см. рис. 6.3) важны не только

229.