Розенберг В.Я. Введение в теорию точности измерительных систем

Подождите немного. Документ загружается.

р*

"31

-л

Для контроля субсистем необхо-

димо располагать значениями до-

пусков, ограничивающими погрешно-

сти конкретных субсистем. Перей-

дем поэтому к рассмотрению задачи

об оптимальном распределении до-

пусков Д»з, г=1, п. Исходным в этой

задаче является требование (6.68),

которое в данном случае удобно

представить в виде

Р[г

з>Дз]=е, (6.96)

где в соответствии с (6.79)

г", = 2 г<з, (6.97)

1 = 1

Рис. 6.6. Графическое решение задачи

об оптимальном распределении по-

грешностей субсистем при ограничен-

ной стоимости системы.

где в свою очередь г

— погрешно-

сти субсистем, которые будем счи-

тать независимыми случайными ве-

личинами.

Требование (6.96) однозначно связывает значения е и Дз. Учитывая

(6.97), получим

ОО 00

6 (Д,) = |

Р (Гз)

Ли = | [Р(ГЧ) *

. • •

* р (г"з)] йгг,

где р(гз) и р(г*з), 1=1, п — плотности вероятности величин г

и г

соответственно; % — символ свертки.

Из (6.96) следует правило контроля систем

(6.98)

(6.99)

Гз

< Дз Я

;

Гз^Дз :фЯ„

где Н

— гипотеза годности системы; Н\ — альтернатива.

Примем аналогичное правило для контроля субсистем

г'з<Д'з=>#

„;

г'.^А'.^Я

где

Н*о

— гипотеза годности /-й субсистемы; — альтернатива; Д*з—

значение допуска для г'-й субсистемы (пока неизвестное). Основываясь

на (6.97), положим

= 2 А

*. (6.100)

1 = 1

Тогда (6.98) можно переписать в виде

2 г'. <2 А'з=фЯ

;

1 = 1 1 = 1

2 г»,

1 = 1 1 = 1

(6.101)

240.

рМ)*

Зафиксируем некоторые значения Д'з (1=1, п). Из (6.101) следует

V* е {О} г

< Д', => Я,. (6.102а)

Обратное утверждение

31'еОТл}: (6.1026)

вообще говоря, неверно, поскольку превышение допуска погрешностью

одной субсистемы может быть случайно скомпенсировано уменьшенны-

ми значениями погрешностей осталь-

ных субсистем.

Отметим, что по этой причине чис-

ло субсистем, входящих в системы, за-

бракованных по правилу (6.98), будет

меньше, чем количество субсистем, за-

бракованных по правилу (6.99).

Таким образом, значения Д

не

определяются однозначно приведен-

ными выше соотношениями. Необхо-

димо дополнительное условие, позво-

ляющее выбрать Д'з единственным и

в каком-то смысле оптимальным обра-

зом. В качестве такого условия при-

мем требование, состоящее в том, что-

бы общая стоимость забракованных по

правилу (6.99) субсистем была мини-

мальной.

Введем следующие обозначения: ег(Д*з)

Ю0%—процент забрако-

ванных по правилу (6.99) 1-х субсистем, зависящий от вероятности

(заштрихованная площадь на рис. 6.7,а)

Рис. 6.7. Определение доли забрако-

ванных субсистем по дифференциаль-

ной (а) и интегральной (б) кривым.

8,(Д',)= { р{г

г)йг'

(6.103)

однозначно-связанный с допуском Д*з (рис. 6.7,6); Сцц— стоимость

одного экземпляра 1-й субсистемы; кг— общее число (тираж) 1-х суб-

систем, подвергаемых контролю. Тогда величина кгег(Д*з) представляет

собой число забракованных 1-х субсистем, а величина

(Д',) = А

8,(Д'

)С«

, (6.104)

— их стоимость. Общая стоимость всех забракованных субсистем

будет

С,(Д>

, = Е С„(Д',) = 2 *|«/(Д',)С

„. (6.105)

1 = 1 1=1

Заметим, что величины кг и Сщ) здесь не зависят от Д*з-

Используя выражения (6.95) и (6.105), мы теперь можем аналити-

чески записать задачу оптимального (по критерию стоимости) распре-

деления допусков в следующем виде

аг% шш С (Д'з,

4'» А»,

1=1

:Д,(«). (6.106)

16—96 241

(6.108)

Решение этой задачи формально ничем не отличается от решения

.задачи (6.91) и совместно с (6.105) имеет вид

1цС

Н1)

с1е1{А

)1с1А

= —Х]

=17л. (6.107)

4. Определение ограничений. Если на всю систему заданы некото-

рые ограничения вида <рг(Л

)<Г/, /=1, 8 (см. (6.68)), то определение

ограничений вида

<р

(А

)<, // = 1,6/ (6.69) на ее субсистемы пред-

ставляет собой задачу распределения ресурсов, решаемую методом

динамического программирования [131 ... 134].

Представляет также интерес другая задача, возникающая при про-

изводстве субсистем универсального применения, когда эти субсистемы

.желательно оптимизировать по собственным характеристикам, независи-

мо от таких факторов, как входной процесс и структура всей системы,

а эти последние факторы учесть в качестве ограничений. При этом же-

лательно найти оценку вида

4 = 1

тде щ — функционалы, играющие роль ограничений, налагаемых на

.входной процесс и характеристики других субсистем и, таким образом,

учитывающие положение 1-й субси-

стемы в системе; — погрешность

1-й субсистемы, не зависящая от ее

положения и выражаемая через ее

собственную характеристику, точнее,

через уклонение реальной характе-

ристики от номинальной. Решение

этой задачи связано с применением

различных неравенств, дающих оцен-

ку сверху погрешностей субсистем,

в результате чего точность систем,

оптимизируемых указанным спосо-

бом, оказывается ниже, чем точность систем, оптимизируемых «прямым

методом» (методом динамического программирования) или методами,

•основанными на определении погрешностей субсистем выражениями

(6.73) или (6.78). Этот вопрос целесообразно рассмотреть на конкрет-

ных примерах, поскольку общие рекомендации дать затруднительно.

Пример 1. Применим полученные соотношения (6.70) ... (6.76) к системе, пред-

ставляющей собой типовое радиотехническое звено, т. е. общий критерий имеет вид

хШ

уШ

а.

ЬрМ

•У

</пМ

Рис. 6.8. Типовое радиотехническое

звено:

а — идеальное; б — реальное.

9(Уж, Ур)=9(\Уж—Ур\)

(6.109)

•а что реальную систему так же, как и номинальную, можно представить типовым

радиотехническим "звеном.

Пусть А

(0> /и(у), §и('0 — характеристика номинальной системы (рис. 6.8,а),

Ы0—характеристики реальной системы (рис. 6.8,6). Согласно (6.65)...

...(6.67), можем записать

УИ

(0 = АиАпАщгХ - |

8а

(I - т) ^ к, (х - I) X (|)

242.

1 1 V

Ур {() = А

РЗ

Р2

1Х = | 8

(( — х) /р | Л

(х — |) х (I) й| Йх.

о [о ^

Используя (6.108) и (6.71), получим

р = р{ _[л

(х-|)х(|)4 й--{^р(^-х)Г

Г|ар(х>

— | (г —

/а

Йх

—

х)

/и

5 М-

йх -

Лр (*-6)*(6) «

Йх

— 6)*(Б)«

(

о Ь

- т "1 1

8в((-*)Гр ^ Л

(х — |) X (|) йх-5^

(^-х)/р

Р -

Л [=Р П еш(*-*) Ь.

|й

(х-|)х(1) й%-

-Г

5 АР(Х-6)Х(5) Й§||ЙХ

_[А р (Х-1)Х(6) Й||1ЙХ

т. е.

р| =

[Ар (0. (Л (0)] =

|л

(х-|)х©й| 1йх ;

р« = р[Ы*Мр(0. {*(<)}] = р( \ и |А

(Х-|)Х(Е)Й1

•/р

Р» =

1ёр (0. ?р (У)' Ар (0. {X (*)}] =

— 8и Гр

З'йр (*-Б)*Ш«*Е

йх

16*

243

Пусть, например, результат измерения — скалярная величина. Тогда согласно

(4.25),

р(|Л

*—А

х\) = |Л

х—А

х\. (6.110)

Оценим р1, р

и р

. Оценка р1 (рис. 6.9) имеет вид

Ь =

5 Аи(*-Ъ)х(1 )й%

-/г

-Гн

Ар (-е

— Б) ж (Е) «

| А

(-«-Е)х(Б)^

•

йг

йг.

хЩ

№

Ч у*;

/и (у) -

Р,

Рис. 6.9. Схема определения погреш-

ности первой субсистемы.

Используя неравенство

I и [У (0] -

Г» [Уо

(011 <

У(()~Уо (01 шах Го (У),

{«}

справедливое для монотонно неубывающих функций, получим

I х

р1

< тах Гв (У) [

8* ((- О Г [Ар (?) -

А>

(|)] * (х -1)

]

йг <

о о

00 оо

< шахГи [у) тах х ({) Г [ (() I йхГ | к

{1) — к

({) | И.

(П {*} $ о

Предполагая оценку несмещенной, на основании (3.84) можем записать

Тогда

р! < тах /'

(у) тах х {() 1

(() — к

(()

сИ.

(П } г.

(6.111)

Для стационарного случайного процесса *(0> применяя к обеим частям неравен-

ства операцию усреднения по множеству {«(/)}, получим

00 со

К<та*Г*(У)М{х({)} (01 Л- Г|М0-М01^

{"} о о

или, для несмещенной оценки,

< М {х (0}тах /'

(у) (' | Н

(0 - А

(0 | Л,

(П г

(6.112)

где функционал 11 к

(I) — к

(() | й( определяет уклонение реальной импульсной реакции

линейной субсистемы от идеальной, а остальные сомножители характеризуют положе-

ние этой субсистемы в системе.

244.

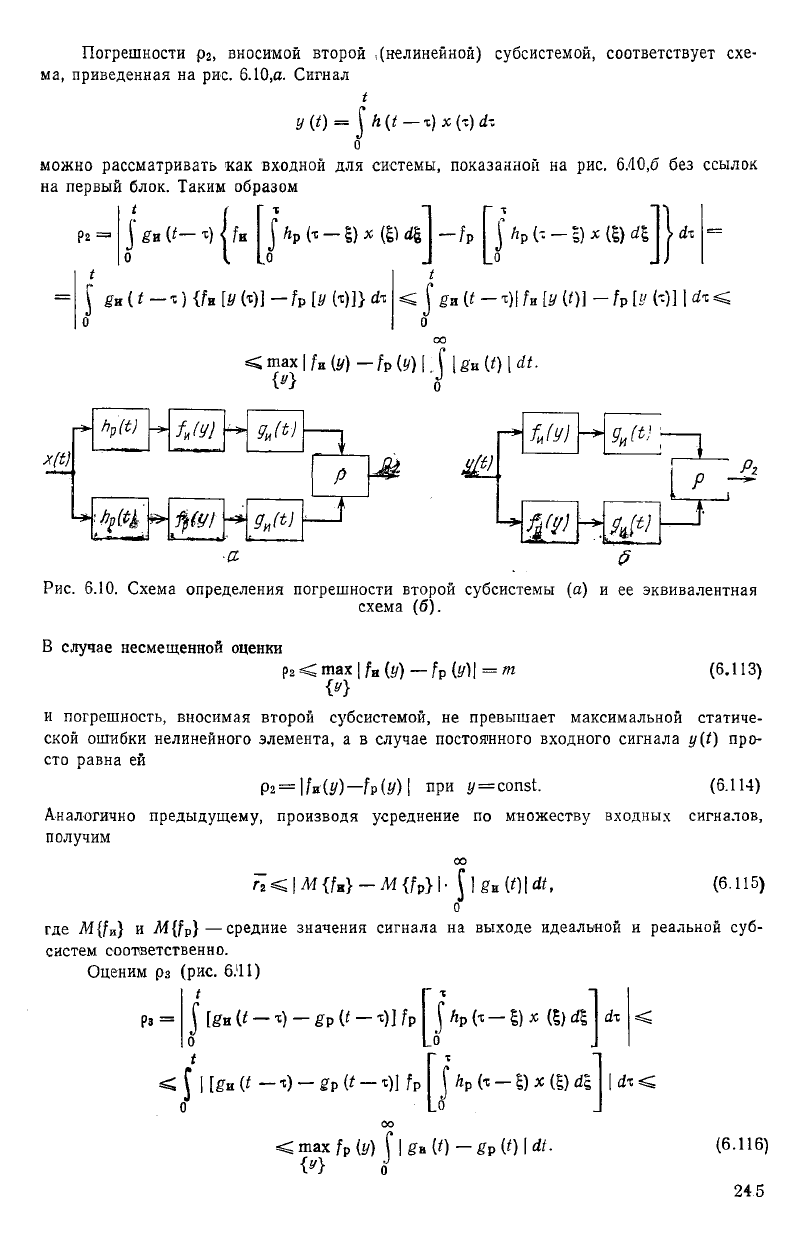
Погрешности рг, вносимой второй .(нелинейной) субсистемой, соответствует схе-

ма, приведенная на рис. 6.10,а. Сигнал

{

у{1) = |й(<-т)х(т) й-.

можно рассматривать как входной для системы, показанной на рис. 6Л0,б без ссылок

на первый блок. Таким образом

* ( Г

= -и ] Лр(- — 1)х (|)

Йх

о I 10

5 ЦЯ ( I -

) Ни [У (х)] -

[р

[У (X)]} йх < |

ёя

(* -

х)|

(01 - Ь \У

[) О

с»

\{*{у)-{р (?/) |, 11 ёи (01^-

,тах |

х[Ъ)

ЫО

щ *

- ....

Ж Ш.

р -

№

и $

РИС. 6.10. Схема определения погрешности второй субсистемы (а) и ее эквивалентная

схема (б).

В случае несмещенной оценки

< тах | /=

{у) — (4г)| = т

(6.113)

и погрешность, вносимая второй субсистемой, не превышает максимальной статиче-

ской ошибки нелинейного элемента, а в случае постоянного входного сигнала у({) про-

сто равна ей

Р2=\[я{у)— Ы</)| при У = СОП31. (6.114)

Аналогично предыдущему, производя усреднение по множеству входных сигналов,

получим

(6.115)

где М{{и} и МУ,}—средние значения сигнала на выходе идеальной и реальной суб-

систем соответственно.

Оценим рз (рис. 6.11)

I [I

| [?. а - х) - Вр (< - х)] !р С Ар (Х- |) х (|)

Рз =

ЙХ

5 О-Ы'-•«)]&> |а

(х-9Х(|)Й5

о Ь

< тах

Гр

(у)

Г I

(о - ^Р

(О I

(И-

{'} о

йх

(6.116)

245.

Усредня , имеем

оо

< М {2} | |

ёи

(1) - ^р (0| Л. (6.117)

Итак, при использовании общего критерия вида (6Л'10) требования к характери-

стикам линейных субсистем ограничивают уклонения в среднем импульсных реакций

соответствующих идеальных и реальных субсистем |(см. (6.Ы1) и (6.112)), а требова-

ние к нелинейной системе ограничивает допустимое уклонение соответствующих ста-

тических характеристик. При этом каждое из слагае-

мых общей погрешности, как это и предусматрива-

лось в самом начале (6.108), состоит из сомножите-

лей, один из которых характеризует «собственную»

погрешность субсистемы, а другие — ее положение

в системе. Последние представляют собой условия

устойчивости линейной системы, ограниченности ха-

рактеристики нелинейного звена в диапазоне мгно-

венных значений входного сигнала и ограниченности

самого входного сигнала системы.

Отдельные субсистемы типового радиотехниче-

ского звена в первом приближении мы представили

в виде схемы, показанной на рис 6.9. Далее оператор каждой субсистемы в свою оче-

редь можно аппроксимировать оператором типового радиотехнического звена (резуль-

таты расчетов представлены в табл. 6.1) или функциональным рядом Винера-Вольтер-

ра [141].

Таким образом, функционалы, оценивающие допустимую степень уклонения тех!

или иных характеристик реальной системы от номинальной, наряду с условиями физи-

ческой реализуемости системы и конечности объема наблюдений, играют роль ограни-

чений, вырабатываемых в процессе комплексирования системы. Аналогичным образом,,

требования ко всей системе (6.68) определяют на этапе решения задачи комплексирова-

ния суперсистемы.

Пример 2. Отказ от учета характеристик входного процесса приводит, как уже-

указывалось, к определенной потере информации о свойствах субсистемы. Проиллю-

стрируем это обстоятельство на примере оценки точности нелинейной безынерционной

системы. Обычно при анализе нелинейных безынерционных систем отклонение харак-

теристики (например, вольт-амперной) /р(х) реальной системы от желательной (или

идеальной) }я(х) оценивают по критерию равномерного приближения (максимального

уклонения характеристик) (6.113).

Такой способ, однако, не позволяет выявить связь величины т с погрешностью

системы, представляющей собой некоторое число (значение функционала), в определе-

нии которого учитывались бы вероятностные характеристики входного сигнала х(1)

(который предполагается стационарным случайным процессом), например, средний риск

Г= У?)р(Уи, ур)лу

йур, (6.Т18)

где I (•) — функция потерь.

Установим связь (6.113) и (6.118), используя предположение о монотонности

характеристик !

(х) и М*) ['142].

Заметим первоначально, что для рассматриваемого класса систем, не обладаю-

щих памятью, р(уя, ур) И 1(у

, Ур) В (6.;1!1®) можно рассматривать не как функцио-

налы, а как обычные функции двух переменных. В результата континуальное инте-

грирование заменяется интегрированием на плоскости.

Учитывая, что

Р(Уш, УТ>)=Р(УК)Р(УР\УП)=Р(У*)6[УР—!р1~

я(у

)],

246.

Рис. 6.11. Схема определения

погрешности третьей субси-

стемы.

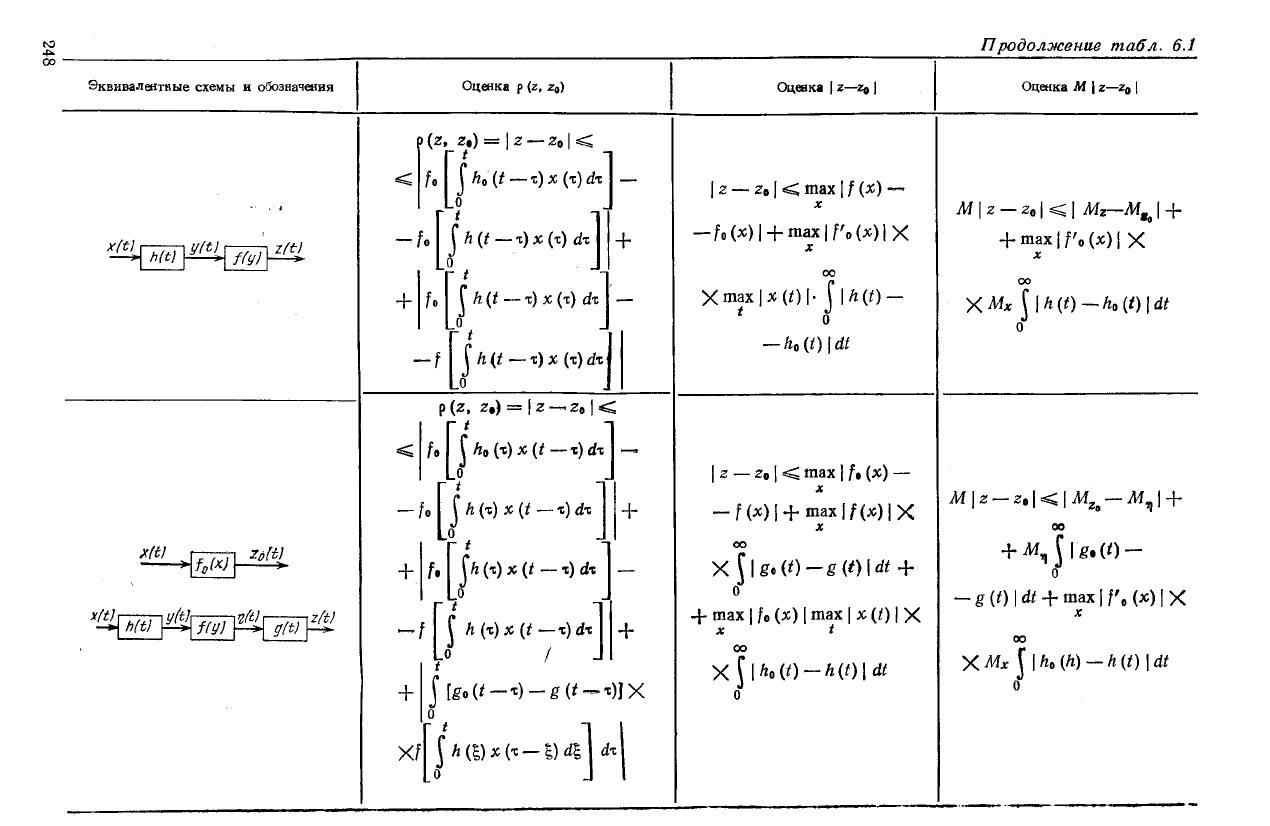
Таблица 6-1

Эквивалентные схемы и обозначения

Оценка р (г, г,)

Оценка | г—г

Оценка М | г—го ]

х(И

и)

ф]

у/и Г——| г (а

ЩЩ^Ш

-47

хМ ГТТП

б№

—" г—

(г, 2

) = | 2 — 2

| <

ГА.

(/ —-с)—Л (^-х)] х(х)йт

^ А

(I — х)

(г) йх —

—

/•

А (<

— г)

(х) йх

р(г, 2

) =

2 —2о

5м*-х) Л [X (х)]-Ял(х)]} ЙХ

[X (х)][А„ (< — х)—Л ({ — х)] ЙХ

р(2, 2

) = | 2 — 2

| <

(1-ъ){1о [Х(х)]-/[х(х)]}й'

{

\Х (х)1 [А„(/-х)-Л(^-х)]йх

:—>

|<шах|х(/)|Х

X ||й(/)-А.(0|Л +

+ тах | / (х) — х |

| г — г

| <тах| / (х)—

-х |.]'|А„(0|Л +

оо

+ тах | / (х)

| •

Г | Л (/)—Ло (() \й1

х л

| 2 — 2

1 < тах | [ (х) —

оо

М |г - г, ||А(0-

—

А„

(0 | М + | Му — Л1г

м |2-2

| |

/г (/) -

—

(0|й/ + |ЛГ* —

оо

- -Ч//1- ]'|М0 |<и

-/о (*)|-$1М0|л -I-

оо

+ тах|/(х)|- Г|Л(/)- А

(/)№

* У

]'|ЛО (01Л

оо •

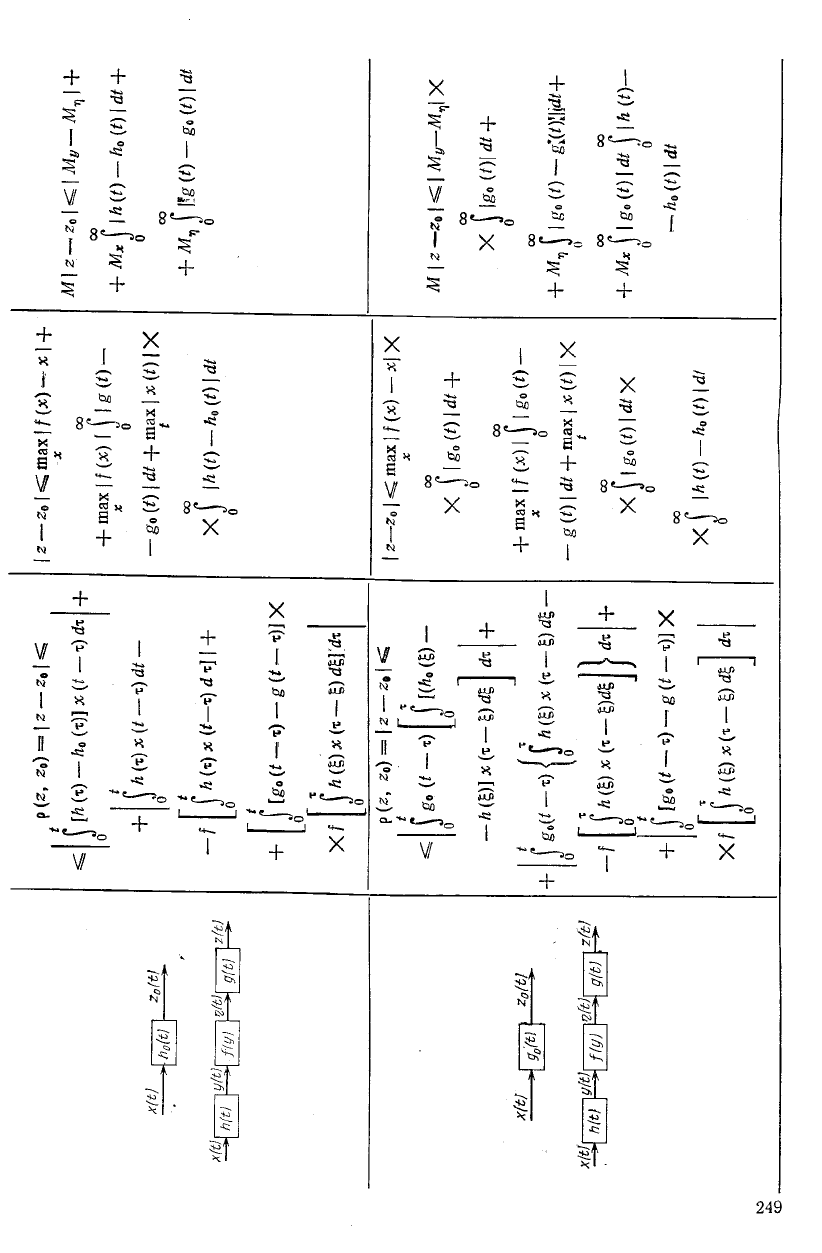
Продолжение табл. 6.1

Эквивалентные схемы и обозначения

Оценка

(г, г

)

Оценка | г—г» | Оценка М | г—г„ |

-и

(г, г,) = | г — г, |<

Гй,(*—х)х(х)Л —

Г' 1

Гн((—1)х(%) ах

и, - х

к {( —

т)

х (г) йъ

• I

| А(г —х)х (т)б(х

(г, 2,) =

2 — 2

^ к„(т.)х(( — х)^ —

-и «)лЛ +

Г (

•г

^к (х) х (I —

х)

йг

С к(г)х(( — г)йг

В / -

| [*.('-'')-«(<—«ИХ

{л(|)х(х-|) й\ ах

| 2 — 2о

< шах

[

Дх) —

—

^о

(х) | + тах | (х)

«л;

X тах \х(1)\- Г|

(0—

' о

—

А»

(<)

|г — г

|<тах|/, (х) —

-Дх)| + тах|/(х)|Х

оо

X С|в.(0-г(01«й +

+ тах

и (*) [

тах

* (О

оо

X {|Ао (0-Л(0|Я

^И

2 — 2„

Л*^

+ тах|Го(х)| X

оо

М\г-г,\<\М

Яв

-М

\ +

-8(0|Л + тах|Г. (*) I X

ХМх (А) —А(0|Л

249.