Розенберг В.Я. Введение в теорию точности измерительных систем

Подождите немного. Документ загружается.

почтительно в виде некоторого числа — значения функционала, опреде-

ленного на множестве р{у

, у

), что обеспечивает возможность постанов-

ки задачи оптимизации ИС. Следует отметить, что в теории оптималь-

ных систем обычно принято считать, что такой критерий задается извне

и обоснование его выбора лежит вне рамок теории.

Однако, имея в виду, что от

выбора критерия зависит не толь-

ко структура ИС, полученная в

результате решения задачи синте-

за (а, стало быть, и результат

измерения), но и особенности си-

стем контроля, требования к суб-

системам, то отсутствие основа-

ний для подобного выбора чрева-

то серьезными осложнениями. На-

пример, при неудачном выборе

критерий может вообще не суще-

ствовать, приводить к многомо-

дальной поверхности отклика, за-

трудняющей поиск экстремума,

оказаться неудобным для теорети-

ческих расчетов или эксперимен-

тальной оценки, быть неадекват-

ным решаемой задаче, т. е. не со-

ответствовать цели, ради достижения которой производится измерение.

Поэтому задачей данной главы являлось, во-первых, выявление возмож-

ных альтернатив, во-вторых, изыскание оснований для предпочтения

одного критерия другому.

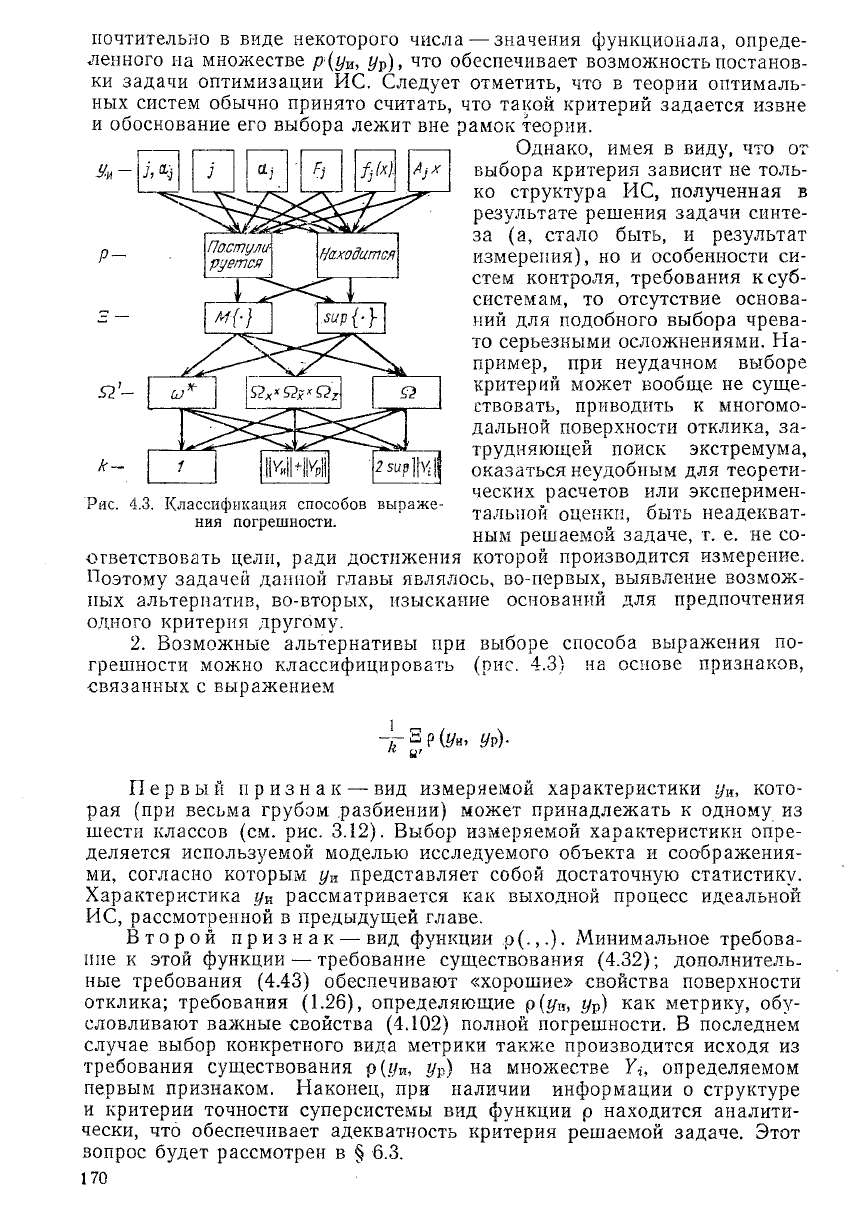
2. Возможные альтернативы при выборе способа выражения по-

грешности можно классифицировать (рис. 4.3) на основе признаков,

связанных с выражением

Я'-

Рис. 4.3. Классификация способов выраже-

ния погрешности.

•ЕР(УИ, УР)-

Первый признак — вид измеряемой характеристики у

, кото-

рая (при весьма грубом разбиении) может принадлежать к одному из

шести классов (см. рис. 3.12). Выбор измеряемой характеристики опре-

деляется используемой моделью исследуемого объекта и соображения-

ми, согласно которым у

представляет собой достаточную статистику.

Характеристика рассматривается как выходной процесс идеальной

ИС, рассмотренной в предыдущей главе.

Второй признак — вид функции р(.,.). Минимальное требова-

ние к этой функции — требование существования (4.32); дополнитель-

ные требования (4.43) обеспечивают «хорошие» свойства поверхности

отклика; требования (1.26), определяющие р(г/и, у

) как метрику, обу-

словливают важные свойства (4.102) полной погрешности. В последнем

случае выбор конкретного вида метрики также производится исходя из

требования существования р(//

, у

) на множестве У г, определяемом

первым признаком. Наконец, при наличии информации о структуре

и критерии точности суперсистемы вид функции р находится аналити-

чески, что обеспечивает адекватность критерия решаемой задаче. Этот

вопрос будет рассмотрен в § 6.3.

170

Третий признак — вид оператора Е, выбираемого в зависимо-

сти от того, имеется или отсутствует информация об априорном распре-

делении (4.9) влияющих факторов, в соответствии с чем Е определяет-

ся выражениями (4.67) или (4.68). Наличие такой информации, соглас-

но (4.129), позволяет уточнить оценку погрешности.

Четвертый признак — вид множества О.' — характеризует

рассматриваемую совокупность влияющих факторов, с учетом которых

оценивается погрешность. В зависимости от й' получаем условные и бе-

зусловные погрешности ИС и типа ИС, а также погрешность измерения

(4.71) ... (4.76).

Наконец, пятый признак — вид нормирующего множителя к —

позволяет определить абсолютную (4.66), относительную (4.110) и

приведенную (4.112) погрешности, причем так, что осложнения, нередко

возникающие при произвольном нормировании, исключаются.

На основе примеров, рассмотренных в главе, можно легко получить

выражения для погрешностей, соответствующих всем возможным ва-

риантам, вытекающим из рис. 4.3.

3. Таким образом, для выбора способа выражения полной погреш-

ности имеются достаточно веские основания, связанные с уточнением

последовательности значений каждого из указанных пяти признакоз.

При этом обеспечивается возможность использования всей имеющейся

у исследователя априорной информации. В наиболее благоприятном

случае, когда используется информация о суперсистеме и распределе-

нии влияющих факторов, полная погрешность наиболее полно характе-

ризует степень близости к конечной цели, достигаемую при использова-

нии данной ИС (данного типа ИС). В любом случае конкретное выра-

жение для полной погрешности, выбранное в результате принятия

некоторой последовательности решений, связанных с классификацией

рис. 4.3, служит основой для решения задач анализа и синтеза, рассма-

триваемых в последующих главах. При этом широко используются

свойства полной погрешности, установленные в § 4.4, в особенности,

свойство (4.102).

Глава 5

АНАЛИЗ ПОЛНОЙ ПОГРЕШНОСТИ

В предыдущей главе мы получили различные определения полной

погрешности измерения, ИС, типа ИС (см. рис. 4.3). Оставаясь в рам-

ках тех же предположений, в частности, предположения о том, что

управление и фиксировано (см. рис. 1.6), необходимо решить задачу

анализа полной погрешности, т. е. указать источники возникновения

погрешности и определить «вклады» (составляющие), вносимые каж-

дым таким источником в полную погрешность.

Указанная задача требует существенного развития и детализации

основой модели процесса измерения с учетом всего процесса создания и

эксплуатации ИС, представляемого в виде последовательности необхо-

димых этапов (выбора модели исследуемого объекта, проектирования,

производства ИС и т. п.), на каждом из которых неизбежно вносятся

погрешности, связанные с несовершенством принимаемых решений, на-

личием ограничений и неконтролируемых возмущений. Определение

этих источников и составляющих погрешности на основе предлагаемого

метода эволюции пространства состояний ИС и составляет основное

содержание этой главы.

Анализ является необходимым этапом задачи оптимизации (синте-

за) ИС, рассматриваемой в следующей главе. Его самостоятельное зна-

чение состоит в возможности вынесения количественных суждений

о реальной точности, достигаемой в процесе измерения.

5.1. АНАЛИЗ ФОРМАЛЬНОЙ МОДЕЛИ ПОГРЕШНОСТИ

Анализ формальной модели погрешности состоит в эксперименталь-

ной оценке (измерении) тех или иных вероятностных характеристик,

связанных с распределением р(г/

, у

), при отсутствии каких-либо дан-

ных о механизме образования результата измерения г/

, рассматривае-

мого как случайный процесс, за исключением, быть может, априорных

сведений о распределении р(х). Иначе говоря, ИС в данном случае

рассматривается как «черный ящик», у которого доступны для наблю-

дения лишь вход и выход.

Наибольшее практическое значение имеет анализ систематической

и случайной составляющих полной погрешности. Весьма общий метод

определения этих составляющих основан на использовании надлежащим

образом выбранных выражений для функционалов положения (3.108,6)

172

и протяженности (3.108,в) распределения р(у

\ур), т. е. величин

УрО

{уи) =Рс[р(Ур\Уа)], (5.1)

Дг/р (Уи) = Ръ

\_р (Ур | Уи) ]

(5.2)

соответственно. Эти функционалы удобно определить выражениями

Уро Ы = аг§ го1П Г р (г/р — у

) р (у

) йу

, (5-3)

Уа

Аг/р(г/и) = / р [УР—УРО(г/и)]р (Ур | г/и)Лур. (5.4)

В выражениях (5.3), (5.4) функцию

р(-) можно рассматривать как некоторую •Р

функцию потерь, выбор вида которой зави.

сит от конкретной ситуации. Предположим

для простоты что у представляет собой

скалярный параметр, и рассмотрим смысл

функционалов г/Ро(г/и) и

г/р

(г/и) для не-

скольких видов функции потерь [31]

(рис. 5.1).

Пример 1. Простая функция

потерь

р—Л—б(у

—уо); й=сопз1>0.

Из соотношения (5.3) следует

[/г —8 (г/р —г/

)]

Рис. 5.1. Виды функций потерь:

/ — простая; 2— модульная; 3— квадратиче-

ская; 4 — прямоугольная.

] ау, РШУш)*Ур = - у-- а

Уо

и на основании известных фильтрующих свойств производной б-функции получаем

Ар (Ур

Ув)

—I

>1°

(.у

— у о)

Р (УР\УО)

ЛУО

= О

йу

= О,

"ро

что является условием максимума функции р(у-р\Уъ) (в предположении ее унимодаль-

ности).

Таким образом, г/

р0

в этом случае совпадает с условной модой, т. е.

с абсциссой наиболее вероятного значения функции

У ре (г/и) = агг тах р (у

]

) Д Мо {г/

| г/

(5.5)

С учетом полученного выражения функционал протяженности (5.4) запишется

в виде

Дур («/•)= | [А — 5 (Ур — Мо {г/р I г/и})] р

(УР

I Уч) йу

= К — р (Мо {г/

|г/и} | Ув), (5.6)

где предполагается /г>р(Мо{г/

|г/

}|г/

), что связано с естественным требованием не-

отрицательности Дг/

(г/„).

Полученный результат физически легко объясним, поскольку экстремальное зна-

чение распределения р(у

\уи) связано с его протяженностью условием нормировки:

чем меньше допустимое значение этого экстремума, тем больше «размазано» распре-

деление по оси г/

, и наоборот. Это соображение подтверждается, в частности, воз-

можностью определения Дг/

(г/

) на основе метода нормированных функционалов (3.77)

173

при и='1 выражением

\ Р{Ур\ Ун) ЛУр I

ЬУв(У*)— иах^^р!^)

(Мо {у

\ г/

}| у

) '

Ур

имеющим ясный физический смысл.

Пример 2. Модульная функция потерь

Р= \Ууг-Уо\.

Имеем

Г й

Ур — У о |

Р(Ур\Уч) Ур = 0,

3 йу о

откуда для г/ро (г/и) получаем соотношение

^ро

(

/и> -

| Р (УР

Уи)

ЛУр

= ) (#р | Уи) йУр — 1/2,

—00

т. е. уро(уш) в этом случае совпадает с условной медианой (50%-ной кван-

тилью) распределения р(ур\у

)

Уро (Уа) Д Ме {у

г/и}. (5-8)

Заметим, что этому методу соответствует использование в -(3.62) весовой функции

вида

I 1, *<0.

1 к

|0, <>0.

Подставляя (5.8) в (5.3), получим

Аг/р(Уи)= ^ | Ур — Ме {ур

г/и}

[

р (у

| г/

) йур-

Пример 3. Квадратичная функция потерь

Р= (УР—г/о)

Из условия

Г Л(Ур —

У»)

. , . .

3 Р(УР\У*)4УР = °

следует

Уро

(г/и) = | УрР

(Ур I

Уи)

ЛУр

= М {ур

}, (5.9)

т. е. функционал положения распределения совпадает с его центром тяжести (услов-

ным математическим ожиданием). Отсюда на основании (5.4) получим

функционал протяженности в виде

ДУр (Уи)= ^ (Ур — М {у

| г/

})2 р (ур | г/н) Лу

. (5.10)

Таким образом Ау(у

) представляет собой второй условный центральный момент (ус-

ловную дисперсию) распределения р(ур\у-л).

Пример 4. Прямоугольная функция потерь. Используем функцию-

потерь вида

р=а—II (у

, А у, у

), (5.11)

174.

где 0<й(=сопз1г^

п/

, , , . /1. |г/

-г/о[<Дг//2,

П (г/о, ДУ, УР) =

, , ^ , о

(О, (г/

—г/

|>Лг/,2.

В данном случае (ср. с (3.65))

(Уро(Уя), &УР(УИ)) = аг2Ш1п Г

(г/о, Ду, г/р)/'(г/р! ?а) ЛУ

, (5.12)

У<АУ->

откуда, как это легко видеть, следует

•"ро^+^р^и)/

^ Р(Ур\ Уа) Лур = Ф [г/ро (г/и) + Дг/р (г/и), 2] — Ф [г/

р0

(;.'

) — Дг/

(г/

)/2]

где [Ф (г) = | р (г/р | у

) йу

— интегральный закон.

—00

Таким образом, с1 представляет собой доверительную вероятность,

а Аур (у

)—доверительный интервал. Величина у ро(.'/и) .'ее с: в;, от

середине доверительного интервала.

Если распределение р(ур\у

) является финитным и в (5.11) положк: . . =', то

Аур(уш) будет совпадать с мерой множества У

, на котором функция р{у

\у

., .

от нуля, т. е. с р а з м а х о м этого распределения (ср. с (3.64)).

Отметим, что для симметричных унимодальных распределений значения урс\у

полученные по формулам (5.5), (5.8), (5.9) и (5.12), совпадают.

Пример 5. Ф у н к ц и я потерь вида (—\пр(ур\у

)).

Интересно рассмотреть также определение функционала протяженности, основан-

ное на выражении (3.148). Имеем

Аур{уж)=ехр{Н(ур\у

)], (5.13)

где Я(у

|г/

)=—/р(у

|г/

) 1п р (г/

уи)с1ур— условная энтропия распределения

Р(УР\УЯ). Полученное выражение совпадает с энтропийной оценкой погреш-

ности [39].

Использование энтропийной оценки оправдано смыслом условной энтропии как

меры неопределенности результата измерения. При этом истинное условное распре-

деление р(ур\уп) результата измерения как бы заменяется эквивалентным ему (рав-

ным по энтропии) равномерным распределением и значение параметра этого распреде-

ления принимается за значение функционала протяженности истинного распределения

Р(УР\УК). Действительно, для равномерного распределения

Рр

(л:) = 1/Л, хе=(0, А) (5.14)

энтропия Я

1п

А, откуда

= е

Р и, полагая Н(ур\у

)=Н

, получаем

= ехр [Я (г/р | г/„)], (5.15)

что совпадает с (5.13).

В качестве одного из аргументов, обосновывающих преимущества энтропийного

критерия, иногда приводят соображение, состоящее в том, что его применение якобы

избавляет от необходимости принятия «волевого» решения, подобного выбору довери-

тельной вероятности при определении доверительного интервала. Это соображение

основано на заблуждении. Действительно, вместо равномерного распределения с рав-

ным успехом можно использовать и какие-либо другие распределения, эквивалентные

Р(УР\УЪ) ПО энтропии. Например, повторяя аналогичные рассуждения для нормального

распределения

^-^-е-^, хб(-со, со) (5.16)

V 2тса

175.

и имея в виду, это энтропия Н

= \пУ2пез, получим

= е

[V 2те. (5.17)

Для экспоненциального распределения

= е

_л:/л

, хб(0, со)

с учетом того, что энергия Я

= ш е Л, будем иметь Л

=е

и т. д.

Таким образом, «волевой акт» присутствует и в данном случае.

В качестве примеров расчета определим Д

<(5Л5), полагая, что р(у?\уж) — нор-

мальное распределение (5.16). Получим

Дэ = К2й»з. (5.18)

Наоборот, находя <т

(5Л7) в предположении, что &{у?\у*) равномерное распределение

(5.14), будем иметь

= Д/К2те. (5.19)

При этом, сопоставляя (5.16) с (5.19), обнаруживаем, что

ДэСГэ

—Ао.

Перейдем к определению условных систематической и случайных

составляющих погрешности ИС, считая исходным выражение (4.71) для

средней условной погрешности

(Ун)

= / Р (Уи, У

) р (у

| Уи)

йур. (5.20)

Подставив в это выражение вместо случайной величины у

значение

функционала положения Уро(Уп), получим определение условной

систематической составляющей п о г р е ш н о с т и ИС

г= (г/и) = р [г/и,

Уро(Уи)

], (5.21)

а взяв вместо у

это же значение Уро(Уи), получим определение услов-

ной случайной составляющей по грешно сти ИС

г Ы = / р [у

о (г/и),

Ур]

(Ур | Уи)

йур. (5.22)

Если р(г/

, г/р)=р(г/и—Ур), то это выражение совпадает с выражением

(5.4) для функционала протяженности.

Поскольку Ур(Уш) •—результат обработки конечного числа п

наблюдений, величина л~(г/

) также является функцией п*)

г„ (г/

) = г_(г/

, я). (5.23)

Отсюда следует, что если экспериментатор имеет возможность выби-

рать число наблюдений, то он может повысить точность за счет умень-

шения случайной составляющей погрешности.

Если

г=Ы= 0, (5.24)

. *> Некоторые удобные для практического применения статистические оценки функ-

ционалов положения и протяженности (рассеяния) в систематизированном виде приве-

дены в [71].

176.

то оценку можно назвать несмещенно й, а если

Нш (г/

/г)

= 0 (5.25)

я-» оо

то состоятельной. Таким образом, при выполнении условий (5.24)

и (5.25) погрешность можно сделать сколь угодно малой путем увели-

чения числа наблюдения. Если же условие (5.24) не выполняется, то

значение систематической составляющей представляет собой тот предел

погрешности, который не может быть превзойден на этом пути.

Впрочем, чаще используют [31] определение несмещенности в виде требования

(5.9)

Уро(УИ) =г/

, (5.26)

а определение состоятельности — в виде

11т Р {\ур —

Уи I

} = 0, (5.27)

л-» со

где 8>0 — сколь угодно малая величина.

'Выражение (5.25) называется условием сходимости по риску, а вы-

ражение '(5.27)—условием сходимости по вероятности. Формулы (5.24)

и (5.25) более общие и более удобные, чем соответственно формулы >(5.26) и ((5.27).

Действительно, М{г/

|г/„} совпадает с г/

только в случае квадратичной функции по-

терь (5.9). С другой стороны, сходимость по вероятности, вообще говоря, не гаран-

тирует сходимости по риску. Последнее означает, что при определенных видах функ-

ции потерь условие (5.27) не позволяет уточнить результат измерения, увеличивая чис-

ло наблюдений.

Величины г

(у

) и г_(у

), определенные соответственно выраже-

ниями (5.21) и (5.22), являются функциями у

(«точки шкалы» ИС).

Для получения безусловных систематической и случайной состав-

ляющих ИС воспользуемся выражением (4.74), определяющим г и г

в зависимости от того, имеется или отсутствует априорная информация

о распределении р(у

)- В соответствии с этим получим выражения для

— средней систематической составляющей погрешно-

сти И С

= М {г

(г/„)} = | р [у„, у

ра

(у

)]р (у

) с1у

]

— максимальной систематической составляющей по-

грешности ИС

= зир г

(у

) = вир

[у

, у

ро

(у„)];

Ув Ув

— средней случайной составляющей погрешности ИС

= М

(У

)}

= ^

[УРО (УИ), УР\ р

(г/и | Ур)

ЙУ

, ЙУР,

— максимальной случайной составляющей погрешно-

сти И С

= вир (у

) = зир |

р [ур

(у,), у

] р (у

) йу

«В Уж

В некоторых случаях, особенно при измерении скалярных величин,

имеется возможность задать «ход» систематической и случайной состав-

ляющих ИС по шкале прибора, т. е. представить их в виде графиков

12—96 177

или формул функций г=(у

) и (г/и) во всем диапазоне измеряемых

ИС значений у

. Этот способ, разумеется, дает больше информации

0 точностных свойствах данной ИС, чем способ задания чисел г, г_,

и г^, хотя и вызывает затруднения при сравнении между собой по

точности двух или более ИС, в особенности ИС, предназначенных для

измерения векторных величин или функций.

Выражения для условных и безусловных систематической и слу-

чайной составляющих полной погрешности ИС, а также условия не-

смещенности (5.24) и состоятель-

ности (5.25) оценки справедливы

не только для случая, когда у

—

скалярная величина, но и в тех

случаях, когда г/

представляет

собой вектор, функцию и т. д.,

в зависимости от чего функция

потерь р(г/

, у

) представляет со-

бой расстояние в соответствую-

щем пространстве, а плотность

р(Уш, Ур)—плотность соответст-

вующего вектора, функционал

плотности вероятности и т. д.

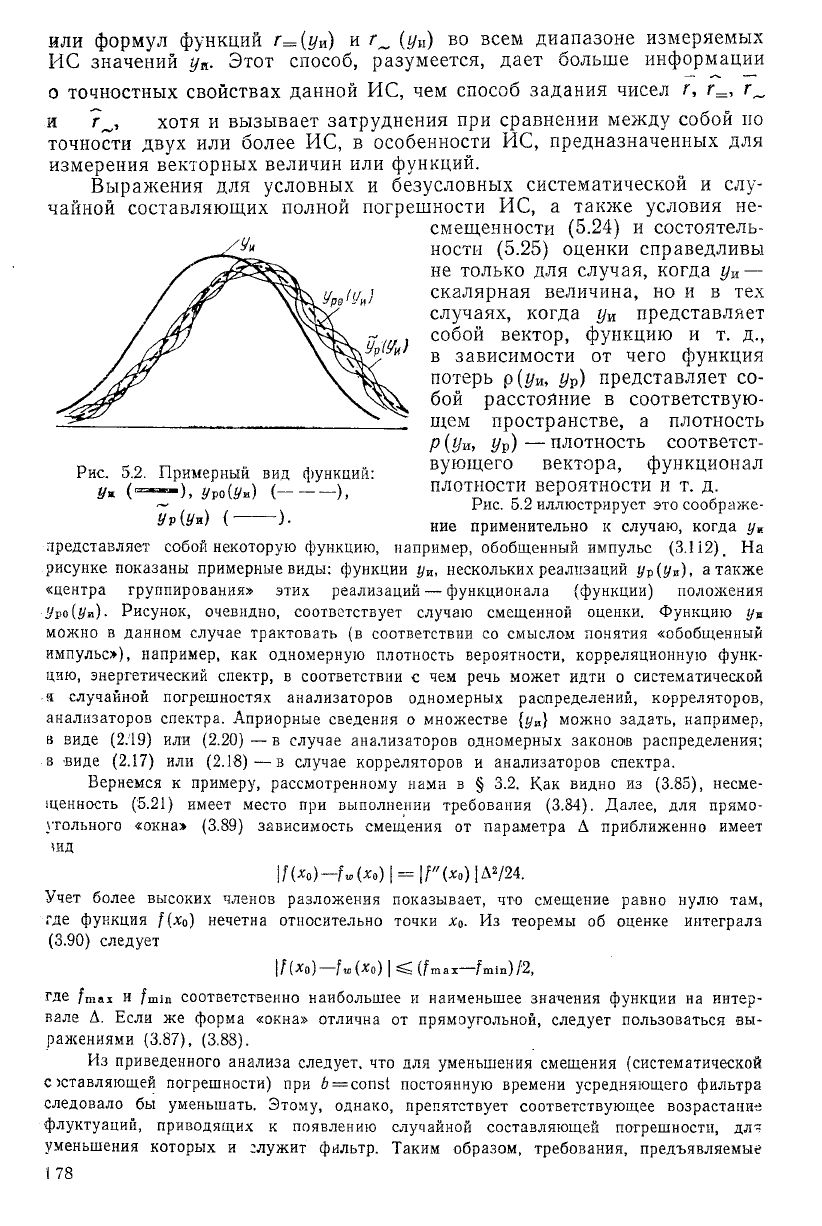
Рис. 5.2 иллюстрирует это соображе-

ние применительно к случаю, когда у

представляет собой некоторую функцию, например, обобщенный импульс (3.112). На

рисунке показаны примерные виды: функции у

, нескольких реализаций у?(уж), а также

«центра группирования» этих реализаций — функционала (функции) положения

Уро(Уи)- Рисунок, очевидно, соответствует случаю смещенной оценки. Функцию г/

можно в данном случае трактовать (в соответствии со смыслом понятия «обобщенный

импульс»), например, как одномерную плотность вероятности, корреляционную функ-

цию, энергетический спектр, в соответствии с чем речь может идти о систематической

и случайной погрешностях анализаторов одномерных распределений, корреляторов,

анализаторов спектра. Априорные сведения о множестве {у

} можно задать, например,

в виде (2.19) или (2.20) — в случае анализаторов одномерных законов распределения;

в виде (2.17) или (2.18)—в случае корреляторов и анализаторов спектра.

Вернемся к примеру, рассмотренному нами в § 3.2. Как видно из (3.85), несме-

щенность (5.21) имеет место при выполнении требования (3.84). Далее, для прямо-

угольного «окна» (3.89) зависимость смещения от параметра А приближенно имеет

шд

|/(*о)-Ы*о)| = |Н*о)|Д*/24.

Учет более высоких членов разложения показывает, что смещение равно нулю там,

где функция [(х

) нечетна относительно точки х

. Из теоремы об оценке интеграла

(3.90) следует

|/(Хо)—Ы*о)

< ([шах—^тт)/2,

где /тах и }тт соответственно наибольшее и наименьшее значения функции на интер-

вале А. Если же форма «окна» отлична от прямоугольной, следует пользоваться вы-

ражениями (3.87), (3.88).

Из приведенного анализа следует, что для уменьшения смещения (систематической

оставляющей погрешности) при 6 = сопз1 постоянную времени усредняющего фильтра

следовало бы уменьшать. Этому, однако, препятствует соответствующее возрастание

флуктуаций, приводящих к появлению случайной составляющей погрешности, дл~

уменьшения которых и служит фильтр. Таким образом, требования, предъявляемые

Рис. 5.2. Примерный вид функций:

у« (=-»-), уМУш) ( ),

У г (Ух) ( )•

к фильтру, противоречивы, ввиду чего необходимо принимать компромиссное решение,

основанное на минимизации полной погрешности. При этом, однако, может оказаться,

что эта погрешность не удовлетворяет требованиям, вытекающим из требований к по-

грешности всей системы, включая систему обработки. Кроме того, при таком способе

мы лишаемся преимуществ, связанных с возможностью воопроизведения функции

^(х) в таком масштабе времени '(обеспечиваемом надлежащим выбором Ь), какой необ-

ходим для согласования с динамическими свойствами системы обработки.

Учитывая, что в подавляющем большинстве случаев п; и измерениях допустима

некоторая задержка результата измерения, можно устранить отмеченное противоречие

следующим образом (метод транспонирования):

1) произвести анализ функции /(х) в течение одного периода развертки с доста-

точно малой скоростью Ь\, выбираемой исключительно из соображений уменьшения

случайной составляющей до допустимого значения (квазистатическнй режим);

2) записать функцию [(х) на промежуточный носитель (запоминающее устрой-

ство) ;

3) воспроизвести полученную запись со скоростью Ъ*, выбираемой исключительно

из соображений, диктуемых условиями работы системы обработки.

При соблюдении указанных требований искажения характеристики за счет си-

стематической я случайной компонент оказываются достаточно малыми.

При анализе качества данного типа ИС необходимо располагать

определениями систематической и случайной погрешностей типа ИС.

Эти составляющие можно получить, применяя оператор Е к соответст-

вующим составляющим ИС, рассматриваемым в данном случае как

случайные величины, реализации которых определяются действием ве-

роятностных механизмов ВМ

и ВМ

(см. рис. 1.6), обусловливающих

образование множества ИС данного типа.

Условные систематическая и случайная составляю-

щие типа ИС, таким образом, определяются выражениями

О/в) = 2 г

(«/„), (5.28)

ХЙ

К„(у.)=Ег„(у

) (5.29)

соответственно, а безусловные систематическая и случай-

ная составляющие типа ИС — выражениями

= Е Я

Ы=

5 Г

=Ы,

Х9

ХЯ

х 2

д;

Хй

ХЕ

соответственно. Далее следует конкретизировать выражения (5.28) ...

(5.31) в зависимости от имеющейся априорной информации о множест-

вах Ож, Ос, каждое из которых можно задать либо границами

(диапазонами) допустимого изменения соответствующих факторов,

либо их априорными распределениями. В зависимости от этого легко

выписать всевозможные очевидные варианты получающихся выраже-

ний. По-видимому, из этих возможных вариантов предпочтение следует

отдать выражениям, связанным с применением оператора математиче-

ского ожидания (т. е. с получением средних характеристик), что, одна-

ко, требует сбора и обработки соответствующего статистического мате-

риала по множеству ИС каждого типа. Заметим, что задание «хода»

систематической и случайной погрешностей для типа ИС с целью

12* 179

(5.30)

(5.31)