Пупенцова С.В. Экономика недвижимости в задачах и примерах

Подождите немного. Документ загружается.

241

ноч-

12. Тарасевич Е.И. А недвижимость.– СПб.: Изд.

«МКС», 2000. – 431 с.

СПбГТУ,

сти.– СПб.: Питер, 2001. –208с.

е рекомендации по определению рыночной стоимости

азателей базисной стоимости по ви-дам работ (УПБС-

и для построения прогнозов в доходном подходе.

НП «Р-Клуб», 2002.

11. Стандарты оценки, обязательные к применению субъектами оце

ной деятельности. Утверждены постановлением Правительства Рос-

сийской Федерации от 6 июля 2001 г. № 519.

нализ инвестиций в

13. Тарасевич Е.И. Оценка недвижимости. – СПб.: Изд-тво

1997. – 422 с.

14. Тарасевич Е.И. Финансирование инвестиций в недвижимость.– СПб

Изд-во СПбГТУ, СПб., 1996. – 240 с.

15. Гранова И.В. Оценка недвижимо

16. Методические рекомендации по оценке эффективности инвестици-

онных проектов (вторая редакция).- Москва.: Экономика, 2000 –

421с.

17. Методически

земельных участков. Распоряжение Минимущества России от

07.03.2002 №568-р.

18. Астахова К.И., Кузнецов Д.Д.. Методическое

пособие. Оценка объ-

ектов недвижимости затратным методом с использованием укруп-

ненных пок

ВР). – МИПК СПбГТУ, 1998.

19. Пупенцова С.В.. Использование регрессионных моделей в методе

сравнения продаж. Статья НЭЖ «Проблемы недвижимости», выпуск

1– СПб.: Изд-во НП «Р-Клуб», 2002.

20. Пупенцова С.В. К вопросу об

использовании общедоступных источ-

ников информаци

Статья НЭЖ «Проблемы недвижимости», выпуск 1– СПб.: Изд-в

242

21. Закон об оценочной деятельности в Ро

Государственной Думой 16 июля 1998 г

пе-

М.: Издательско-книготорговй центр «маркетинг»,

ценка недвижимости: Учебник

. Под ред. Грязновой А.Г., Федото-

бГТУ,2000. 80 с.

.. –

ссийской Федерации. Принят

. Одобрен Советом Федера-

ции 17 июля 1998 г.

22. Горемыкин В.А. Экономика недвижимости: Учебник. – 2-е изд.

рераб. и доп. –

2002.–804 с.

23. Александров В.Т. Ценообразование в строительстве.– СПб: Питер,

2001.–352 с.

24. О

вой М.А. – М.: Финансы и статистика, 2002. – 496 с.

25. Озеров Е.С. К вопросу о выборе наиболее эффективного варианта

использования объекта при оценке и управлении недвижимостью.

НЭЖ «Проблемы недвижимости», вып. 3: Изд. НП «Р-Клуб», 2000 г.

26. Каленкевич М.В. Экономика недвижимости. Программа управления

объектом смешанного

назначения. Учебное пособие, СПб.: Изд-во

СП

27. Предынвестиционные исследования и разработка бизнес-плана инве

стиционного проекта. Щелков В.С., Белоусов Л.М., Блинков В.М

М.: ЗАО «Финстатинформ», 1999.–248 с.

28. Четыркин Е.М. Статистические методы прогнозирования. Изд. 2-е,

переаб. и доп. М., «Статистика», 1977 – 200с.

243

ца статистических функций в Excel.

ула Функция в Excel

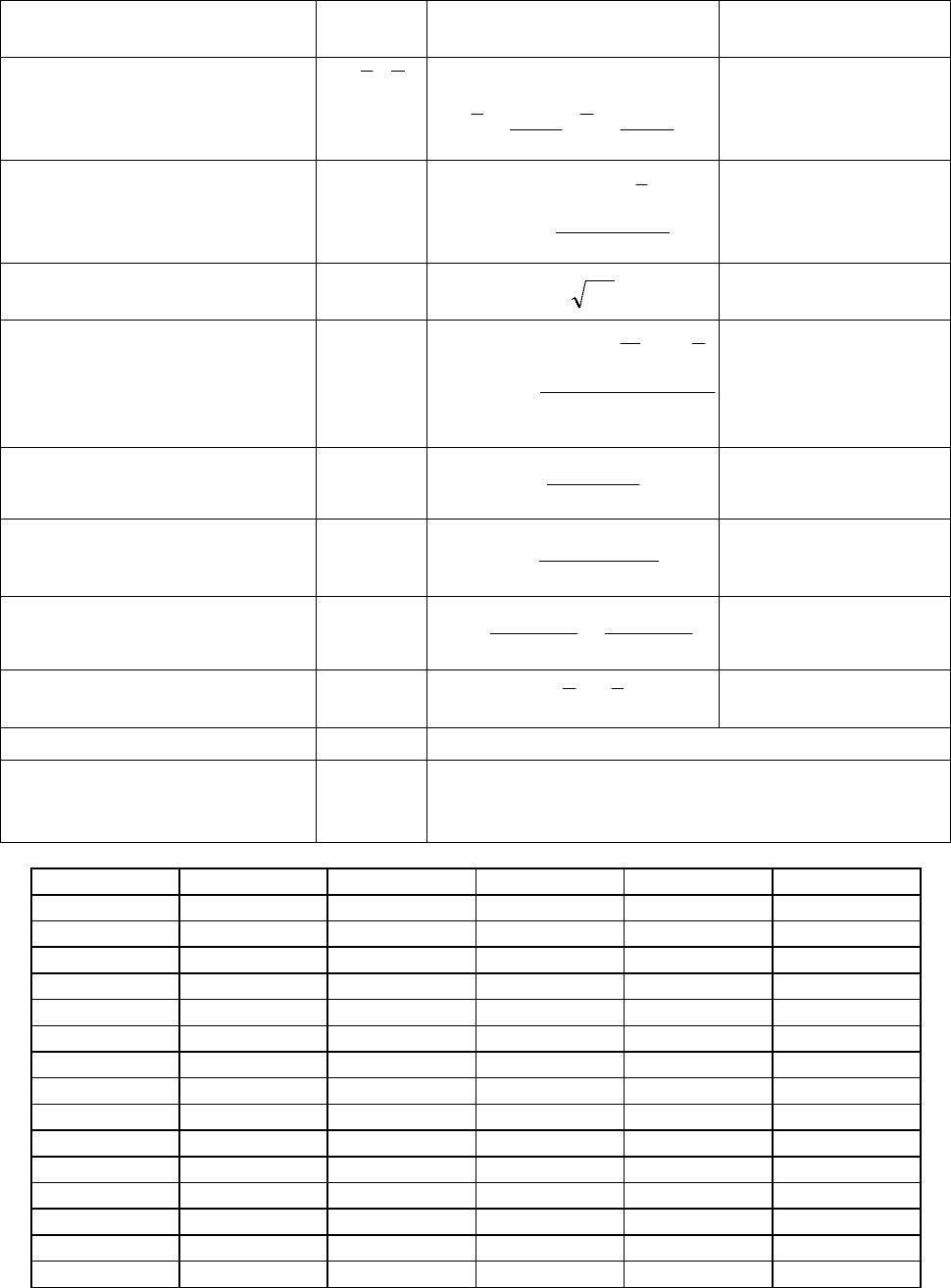
ПРИЛОЖЕНИЕ 1. Табли

Наименование

ние

Форм

Обозначе-

Среднее значение

, х , y

здесь:

ср

., y

ср

= ,

∑

СРЗНАЧ(массив X)

Дисперсия

var(x

, s

)(

=σ

)( −

∑

ДИСПР(массив X)

Сред

дарт

неквадратическое (стан-

ное) отклонение

СКО,

, s

σ=σ

СТАНДАРТОТКЛОНП

(массив X)

Кова

yyxx

)()( −−

∑

),cov(

(массив Y; мас-

сив X)

КОВАР

риация cov(x,y)

Коэф

)()(

),cov(

σσ

фициент корреляции

КОРРЕЛ(массив Y;

массив X)

Коэффициент детерминации

)()(

σσ

),v(

КВПИРСОН(массив Y;

массив X)

Коэф

х в у

фициент β, переменная при

)(

xσ

ar(

),ov(

НАКЛОН(массив Y;

массив X)

c),cov(

==β

равнении линейн. регрессии

Коэффициент

урав

α, свободный член

xy β−=α

массив X

нения линейной регрессии

ОТРЕЗОК(массив Y;

)

t-критерий Стьюдента

СТЬЮДРАСПРОБР(0,05; n-1), для р=0,95

Крит

ерий Фишера, критический

сти

=0,05 (р=0,95) и степенями свободы k

FРАСПРОБР(0,05; k

; k

), для заданного уровня знач

=m, k

=n-

m-1, где n-число наблюдений, m – число факторов

Критерий Стьюдента (n – количество объектов в выборке, р – заданная вероятность)

n t, р=0,95 t, р=0,99 n t, р=0,95 t, р=0,99

3 4,302656 9,924988 18 2,109819 2,898232

4 3,182449 5,840848 19 2,100924 2,878442

5 2,776451 4,604080 20 2,093025 2,860943

6 2,570578 4,032117 21 2,085962 2,845336

7 2,446914 3,707428 22 2,079614 2,831366

8 2,364623 3,499481 23 2,073875 2,818761

9 2,306006 3,355381 24 2,068655 2,807337

10 2,262159 3,249843 25 2,063898 2,796951

11 2,228139 3,169262 26 2,059537 2,787438

12 2,200986 3,105815 27 2,055531 2,778725

13 2,178813 3,054538 28 2,051829 2,770685

14 2,160368 3,012283 29 2,048409 2,763263

15 2,144789 2,976849 30 2,045231 2,756387

16 2,131451 2,946726 n>30 р=0,95 р=0,99

17 2,119905 2,920788 t 1,959961 2,575835

244

мимущество Российской Федерации Администрация Санкт-Петербурга

997 года N 1293-р

процесса в Санкт-Петербурге и во

анкт-Петербурга от 04.04.97 N 283-р

ении предоставления

объектов недвижимости и имущественных

я для оценки

ов недвижимости офисного и торгового назначения

(далее - ение).

а дисконтирования при рыночной оценке объектов недвижимости,

кой.

урга, за исключением объектов, ука-

занн от-

имущества, находящегося в государственной соб-

Председатель

ета Г.О.Греф

ПРИЛОЖЕНИЕ 2. Расчет ставки дисконтирования по методике КУГИ

Госко

КОМИТЕТ ПО УПРАВЛЕНИЮ ГОРОДСКИМ ИМУЩЕСТВОМ

РАСПОРЯЖЕНИЕ

от 21 ноября 1

Об утверждении методики определения ставки дисконтирования

В целях активизации инвестиционного

исполнение п.5 распоряжения губернатора С

"Об упорядоч

прав на них на инвестиционных условиях":

1. Утвердить Методику определения ставки дисконтировани

рыночной стоимости объект

Методика) (Прилож

Установить, что:

2.1. Ставк

находящихся в собственности Санкт-Петербурга, офисного и/или торгового на-

значения площадью

менее 10000 кв.м, не имеющих уникальных особенностей,

значительно влияющих на их потребительскую ценность, определяется в соот-

ветствии с Методи

2.2. Ставка дисконтирования при рыночной оценке объектов недвижимости,

находящихся в собственности Санкт-Петерб

ых в п.2.1 настоящего распоряжения, определяется индивидуально в со

ветствии с распоряжением губернатора Санкт-Петербурга

от 01.08.96 N 113-р "О

порядке оценки недвижимого

ственности, и прав на него".

3. Контроль за исполнением настоящего распоряжения оставляю за собой.

Комит

245

Приложение к распоряжению

ядок расчета

Санкт-

ного и/или торгового на-

знач

с разделами 2 и 3 Методики. Ставка дисконтирования для оценки объектов, рас-

ределяется в соответствии с распоря-

1.08.96 N 113-р "О порядке оценки

а, находящегося в государственной собственности, и

пр

По ке понимается ожидаемая инве-

сто ций в оцениваемый объект недвижимости.

вной частью города в данной Методике понимается территория

н-

исходные

КУГИ от 21.11.97 N 1293-р

П.3.1. Методика определения ставки дисконтирования для оценки рыночной

стоимости объектов недвижимости офисного и торгового назначения

1. Общие положения

Настоящая методика (далее - Методика) устанавливает пор

ставки (нормы) дисконтирования, применяемой при рыночной оценке объектов

недвижимости, находящихся в государственной собственности

Петербурга.

Ставка дисконтирования для оценки объектов

офис

ения, расположенных в основной части города, определяется в соответствии

положенных вне основной части города, оп

жением губернатора Санкт-Петербурга от 0

недвижимого имуществ

ав на него".

д ставкой дисконтирования в данной Методи

ром норма прибыли от инвести

Под осно

Центрального, Адмиралтейского, Петроградского, Василеостровского, Калини

ского, Кировского, Выборгского, Невского и Фрунзенского районов города

Санкт-Петербурга, а также зоны многоэтажной городской застройки

Красно-

сельского, Московского, Приморского и Красногвардейского районов.

2. Исходные данные для расчета

Для расчета в соответствии с Методикой необходимы следующие

данные:

2.1. Тип оцениваемого объекта (далее - объекта).

2.2. Точный милицейский адрес объекта.

246

ах годовых);

,1% - для офисной функции;

та;

я от центра города;

бъекта;

и расположения объекта;

ффициент влияния объема требуемой реконструкции объекта.

ся ставки дисконтирования для оценки рыночной стоимости

2.3. Общая площадь объекта.

2.4. Существующее состояние объекта.

2.5. Оптимальность расположения объекта.

2.6. Объем реконструкции объекта.

3. Порядок расчета ставки дисконтирования

3.1. Ставка дисконтирования определяется по формуле:

Y = Y(б) х К(1) х К(2) х К(3) х К(4) х К(5) х К(6),

где:Y - ставка дисконтирования для оценки рыночной стоимости объекта (в

процент

Y(б) - базовая

ставка дисконтирования (в процентах годовых):

Y(б) = 29

Y(б) = 30,7% - для торговой функции;

К(1) - коэффициент влияния типа объек

К(2) - коэффициент влияния расстояни

К(3) - коэффициент влияния площади о

К(4) - коэффициент влияния состояния объекта;

К(5) - коэффициент влияния оптимальност

К(6) - коэ

3.2. В

случаях когда часть объекта имеет офисное назначение, а другая тор-

говое, определяют

каждой из частей согласно п.3.1. Ставка дисконтирования для оценки рыночной

стоимости всего объекта определяется по формуле:

Y (оф) х S(оф) + Y(т) х S(т)

Y(0) = ----------------------------,

S(оф) + S(т)

где: Y(0) - ставка дисконтирования для оценки рыночной

стоимости всего

объекта;

Y(оф) - ставка дисконтирования для оценки рыночной стоимости офисной

части;

247

Определение коэффициента влияния типа объекта К(1)

Коэф

х-1)* - для офисной функции;

Х - код типа объекта:

ения.

При

Под типом объекта понимается ектом оценки является здание

ределении ставки дисконтирования для каждой из частей они считают-

ся как здания.

Если -

т считать встроенное помещение.

5. О

Коэффицие я офисной функции

рассчиты е

К(2) = 1, )_3),

где R - к ло-

метрах);

е - основание натурального логарифма (е примерно равно 2,71828).

Для торговой функции К(2) принимается равным 1.

Y(т) - ставка дисконтирования для оценки рыночной стоимости торговой

части;

S(оф) - общая площадь офисной части объекта (в квадратных метрах);

S(т) - общая площадь торговой части объекта (в квадратных метрах).

фициент влияния типа объекта К(1) определяется по формуле:

К(1) = 1,05_(2

К(1) = 1,06_(2х-1)* - для

торговой функции,

----------------

* Здесь и далее в приводимых формулах знак "_" - следует

понимать как степень. Примечание юридического бюро "Кодекс".

где:

Х = 0 - для здания;

Х = 1 - для встроенного помещ

мечания:

здание, если объ

целиком. Если одна часть здания имеет офисную функцию, а

другая торговую,

то при оп

для

объектом оценки является отдельное встроенное помещение, типом объек

та следуе

пределение коэффициента влияния расстояния от центра города К(2)

нт влияния расстояния от центра города К(2) дл

ва тся

по формуле:

02_(1-2 х е_(-(0,19 х R

ратчайшее расстояние по прямой от объекта до центра города (в ки

248

Примечание

Под расстоя тодике принято расстояние до

осевой л ди

Во ской системе координат:

113481, 94416; 116249,93751.

6. Определение коэффициента влияния площади объекта К(3)

Коэффициент влияния площади объекта К(3) определяется по формуле:

К(3) = 1,03_(1,004-2,004 х е_-(0,00025 х S)_1,08) - для

офисной функции;

К(3) = 1,04_(1,094-2,35 х е_(-(0,0015 х S)_0,095) - для торговой функции,

где: S - общая площадь объекта (в квадратных метрах).

7. Определение коэффициента влияния состояния объекта К(4)

Коэффициент влияния состояния объекта К(4) определяется по формуле:

К(4) = 1,06_(Q-1) - для офисной функции;

К(4) = 1,097_(Q-1) - для торговой функции,

где: Q - код состояния:

Q = 0 - для хорошего состояния;

Q = 1 - для удовлетворительного состояния;

Q = 2 - для

плохого состояния.

Примечание:

Для целей Методики используются следующие категории состояния объекта:

Хорошее состояние - объект полностью пригоден к использованию по функцио-

нальному назначению без проведения ремонта. Износ несущих конструкций и

инженерных сетей отсутствует или незначителен. Отделка может иметь незначи-

тельные дефекты (волосные трещины, сколы штукатурки, единичные поврежде-

ния окрасочного слоя, царапины, отдельные

мелкие повреждения покрытий стен

и полов). Для новых объектов возможно отсутствие чистовой отделки.

Удовлетворительное состояние - объект может эксплуатироваться без проведе-

ния ремонта, однако имеет дефекты, устранимые с помощью текущего ремонта.

Имеется износ несущих конструкций и инженерных сетей, который требует про-

нием до центра города в настоящей Ме

инии Невского проспекта от Адмиралтейского проспекта до площа

сстания. Координаты начала и конца линии в Балтий

249

штук

Плохое состояние - о ко с помощью капи-

тального ремон меется значи-

тельный износ элементов несущих конструкций и инженерных сетей, однако

эксплуатация объекта в существующем ии не запрещена или возможна

после

проведения выборочного капитального ремонта.

8.Определение коэффициента влияния оптимальности расположения объек-

та К(5)

Коэффициент влияния оптималь бъекта К(5) определяется

о формуле:

К(5) = 1,156_(L-1) - для офисной функции;

К(

где: L - код

L = 0 - для оптимального расположения;

L = 1 - для расположения средней оптимальности;

L = 2 - для неоптимального расположения.

При

Для елей Методики используются

следующие категории оптимальности распо-

лож

Под оптимально расположенным понимается ъект, имеющий набор факторов

расположения и окружения, которые являются наибол

сматриваемого оценщиком использования объекта. Состав и качественная ха-

рактеристика этих факторов в ближайшем будущем не ухудшится.

Под среднеоптимально расположенным онимается объект, расположение кото-

рого не является в полной

мере рассматриваемого использова-

ния, однако позволяет приносить ста ый доход от аренды. В ближайшей

перспективе не ожидается значительного изменения существующего окружения

объекта.

ведения текущего ремонта объекта. Отделка требует проведения внутренни

атурных, облицовочных и малярных работ.

бъект имеет дефекты, устранимые толь

та. Здание находится в предаварийном состоянии, и

состоян

ности расположения о

5) = 1,197_(L-1) - для торговой функции,

оптимальности расположения:

мечание:

ения объекта:

об

ее оптимальными для рас-

оптимальным для

бильн

250

Под неоптимальным расположенным понимается объект, имеющий окружение,

сдерживающее развитие рассматриваемой оценщиком функции использования.

В перспективе возможно ухудшение существующего состояния окружения, что

может сделать рассматриваемое использование объекта в этом месте убыточ-

ным.

9. Определение коэффициента влияния объема требуемой реконструкции

объекта К(6)

Коэффициент влияния об объекта К(6) определя-

ется по формуле:

К(6) = 1,075_(1-2 х е_(-(0,0045 х V)_3,5) - для офисной функции;

К(6) = 1,07_(1,0008-2,0008 х е_(-(0,0045 для торговой функции,

где:

V - объем требуемой реконстру у оценки (в долларах США на

1 квадратный метр общей площади).

П.3.2. Пример расчета ста я по методике КУГИ в про-

Программа реализована в электронных и разработана на

кафедре

ЭМН.

Исходные данные, которые необходимы для расчета ставки аренды в про-

грамме:

ре-

щения);

про-

грамме есть подсказка;

ъема требуемой реконструкции

х V)_3,5) -

кции объекта на дат

вки дисконтировани

грамме кафедры

таблицах Excel

− координаты объекта в Балтийской системе координат, можно оп

делить по карте, см. лабораторную работу № 1;

− тип здания (здание целиком или встроенные поме

− площадь объекта;

− состояние объекта (хорошее, удовлетворительное, плохое), в