Пупенцова С.В. Экономика недвижимости в задачах и примерах
Подождите немного. Документ загружается.


171
окое значение R
2
, необходимо проверить его на значимость.
Для проверки значимости вычисляют с
Этап 2. Прежде, чем делать вывод о качестве регрессионной модели, не-
смотря на выс
татистику F-критерий Фишера. Рас-
четное значение критерия Фишера сравнивают с табличным (критическим), если
расчетное значение больше критического (F
расч
.> F
крит
.), то уравнение регрессии
принято считать значимым.
m
mn
Q
Q
F
регр
расч
1
.
.
−−
×=
ост.
(6.2)
где n – число наблюдений, m – чи
таточной суммы квадратов отклонений Q
ост
с Q
регр
показывает, во сколько раз
регр казывает результат лучше, чем среднее значе-
ние y
с
.
Критическое
крит.
выбранным уровнем -
чимости α и степен
ределить в Excel с
а критерий Фишера равен
сло факторных признаков. Сравнение ос-
ессионная зависимость предс
р.
значение критерия Фишера F
с зна
ями свободы k
1
= m и k
2
= n-m-1 можно оп
помощью функции =FРАСПРОБР(α; k
1
; k
2
).
Для рассмотренного пример
1
1132
348
8974
−−
×=
=774, F
.расч
F
д, что
регр
-
тель
регрессии (проверка ги-
поте
крит.
= FРАСПРОБР (0,05;1;30) = 4,17. Следовательно,
значение коэффициента R
2
статистически значимо и можно сделать выво
ессионная зависимость объясняет на 96% изменение ставки аренды измене-
нием расстояния от станции метро.
Если значение R
2
незначимо, то следует анализировать иные влияющие
факторы, либо провести оценку выборки с помощью расчета среднего и довери
ного интервала.
Этап 3. Если значимость регрессионной связи установлена, то следующий
шаг анализа – это проверка значимости коэффициентов
зы о равенстве нулю коэффициентов уравнения регрессии), которая осуще-
ствляется с помощью критерия Стьюдента
.
Вычисляется статистика t=β / S
yβ
,
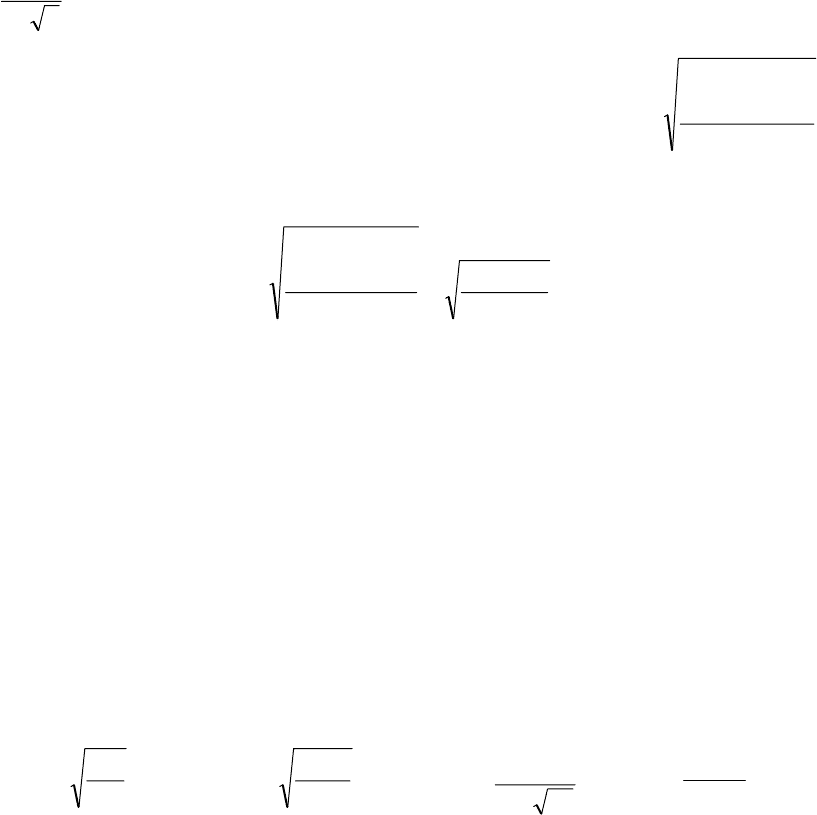
172
где β – проверяемый на значимость коэффициент уравнения регрессии;
n
S
x
y
y
σ
β
S =
онение уравнения регрессии;
– оценка среднеквадратического отклонения коэффициента β; S
y
– cр-
еднеквадратическое откл
n
xx
n
2
)( −
∑
ср
i
i
x
.
1
=
=
σ
– сред-
неквадратическое отклонение фактора x.
11 −−−− mnmn
y
)
.
2
=
−
Q
y
ост
xii
(6.3)
Затем расчетный критерий t сравнивают с критическим критерием
k
, най-
денным по расп ления Стьюдента (по уров значимости и чис-
лу степе свободы k= число факторных признаков, n – чис блю-
дений )
фициент считается значимым.
t
α
,
k
,=СТЬЮДРАСПОБР(0,05;31)=2,04
(
1
=
∑
y
S
n
t
α
,
таблицам реде ню α
ней n-m, m – ло на
) и спользуя функцию Excel: =С ДРАСПО ;k . Если |ли и ТЬЮ БР(α t| ≥ t
α
,
k
, то
нулевую гипотезу о равенстве коэффициента регрессии нулю отвергают и коэф-
Проверим значимость коэффициента уравнения β.
711
32
5693
,
,
==σ
x
, 4053
30
348
,==
y
S ,
350
32711
4053
,
,
,
==
βy
S ,
t= 8227
350
799
,
,
,
−=
−
В нашем примере ставка аренды
Видно, что ⏐t⏐=27,82> t
α
,
k
,=2,04, для коэффициента α: ⏐t⏐= 432,1 >
t
α
,
k
,=2,04, следовательно. коэффициенты уравнения значимы, и полученное
уравнение может быть использовано для определения ставки аренды для анало-
гичных объектов.
для торгового павильона, расположенного
на расстоянии 0,8 км от станции метро, равна y=449,07-9,79×0,8=441,24 $ за м
2
в
год.

Этап 4. Следует отметить, что расчет стоимости объекта оценки статисти-
ческими методами по регрессионной модели предполагает интервальную оцен-
ку, где с заданной вероятностью будет лежать исходная величина.
Границы доверительного интервала уравнения регрессии можно рассчитать
по формуле:
kStyy
yaxi
±
=
±
, (6.4)
где y
xi
– расчетная ставка по уравнению регрессии, S
y
– среднеквадратическое
отклонение от уравнения (2); t
α
– t-критерий Стьюдента для заданного уровня
значимости α и числа степеней свободы (n-m-1), n – число уровней ряда, m –
число факторов (для линейного уравнения m=1)
∑
=
−
−
+
+
=
n
i
срi
срi
xx
xx
n
n
k
1
2
2
.
)(
)(
1
, (6.5)
Для оцениваемого объекта:
t
α
=
СТЬЮДРАСПОБР(0,05;30)=2,04; S
y
=3,405; k= 0291
55993
41280
32
33
2
,
,
),,(
=
−
+
;
y=441,24±2,04×3,405×1,029=441,24±7,148.
Вывод: рыночная ставка аренды объекта оценки с вероятностью 95% будет ле-
жать в доверительном интервале: 441±7.
Представим информацию графически (рис. 6.3.5): объект оценки (большая
круглая точка), доверительный интерв регрессии и доверитель
ный
х функций аналогичен.
ал для уравнения -
интервал для среднего значения (линии, параллельные оси абсцисс).
Рассмотренный пример выполнен для однофакторной модели и
иллюстри-
рует алгоритм регрессионного анализа. В случае многомерной регрессии расче-
ты каждого этапа усложняются, та что более простым способом оказывается ис-
пользование стандартных статистических функций и Пакета анализа в Excel.
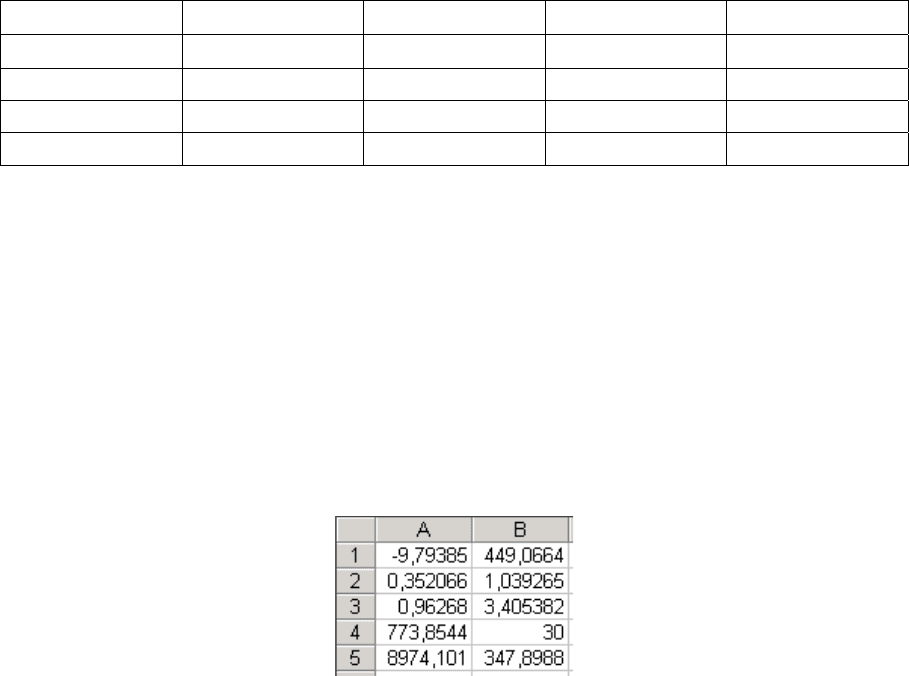
Параметры уравнения линейной (экспоненциальной) регрессии можно по-
лучить, используя функцию массива – ЛИНЕЙН (ЛГРФПРИБЛ). Алгоритм
применения обеи
173
174
Функция ЛИНЕЙН линейной функци-
ей. Д
х; ко
жь» для α = 0; статистика – «Истина» для вывода рег-
ресс
…
β
1
α
аппроксимирует имеющиеся данные
ля вывода таблицы результатов перед обращением к формуле надо выде-
лить диапазон ячеек (m+1 строк и 5 столбцов).
Синтаксис функции: ЛИНЕЙН(известные значения y; известные значения
нст; статистика), где известные значения y – множество значений Y; из-
вестные значения х –множество значений Х; конст
– «Истина»(или опущено)
для вычисления α; «Ло
ионной статистики:
После ввода значений в формулу, вместо привычного «ENTER» надо нажать
три клавиши одновременно «CTRL+SHIFT+ENTER». В выделенном диапазоне
покажется таблица результатов.
Эта таблица содержит следующую информацию:
β
m
β
m-1
S
β
m
S
β
m-1
…
S
β
1
S
α
R
2
S
y
#Н/Д #Н/Д #Н/Д
F
расч.
k
2
=n-m-1 #Н/Д #Н/Д #Н/Д
Q
рег.
Q
ост.
#Н/Д #Н/Д #Н/Д
Здесь α – угол наклона или свободный член уравнения; β
1
, β
2
, …,β
m
– коэф-
фициенты уравнения регрессии; S
β
1
,S
β
2
,...,S
β
m
– cтандартные значения ошибок для
коэффициентов β
1
, β
2
,..., β
m
; S
α
– стандартное значение ошибки для постоянной α
(S
α
= #Н/Д, если «конст» имеет значение ЛОЖЬ). Остальные обозначения введе-
ны выше.
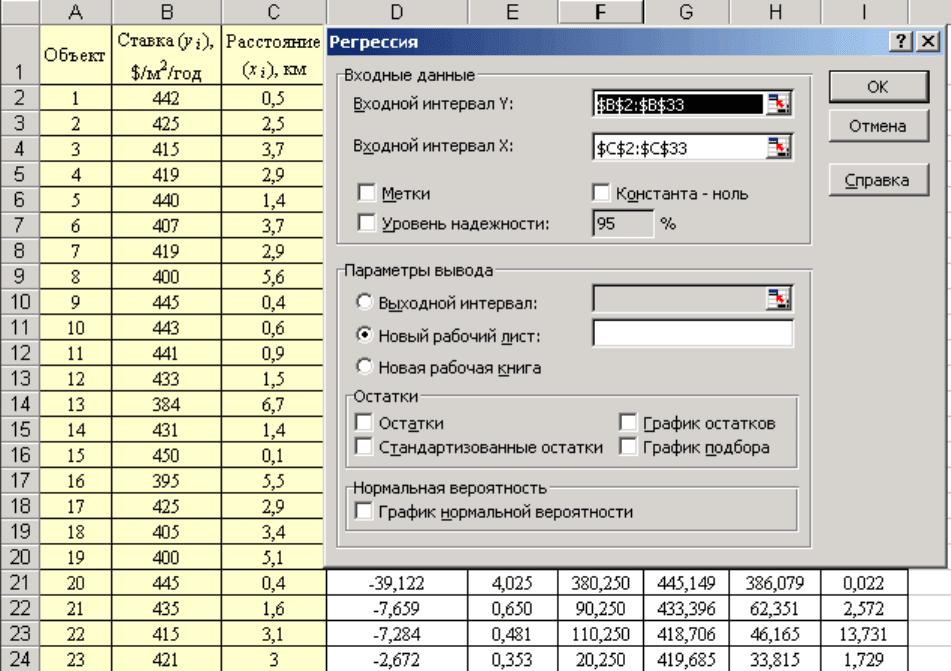
Ниже приведена таблица результатов для нашего примера, полученная с
помощью функции ЛИНЕЙН.
175
стоятельно проверить значимость коэффициен-
та де
информацию можно получить, используя «Пакет анали-
за».
ать из списка Инструменты анализа Регрессию.
На э
Прежде чем применять данные, выведенные в таблице функцией ЛИНЕЙН
(ЛГРФПРИБЛ), необходимо само
терминации R
2
и коэффициентов уравнения α и β
i
.
Наиболее полную
Рассмотрим применение регрессионного анализа на том же примере. Чтобы
воспользоваться этим инструментом, необходимо убедиться, что активизирован
«Пакет анализа», команда Сервис
⇒
Надстройки. Затем выполнить команду
Сервис
⇒
Анализ данных. Выбр
кране появиться диалоговое окно (рис. 7.)
Рис. 6.3.7
В текстовое поле «Входной интервал Y» необходимо ввести массив резуль-
тиру
жности» было
введено 95 и переключатель «Параметры вывода» установлен в положение
ющей переменной. В текстовое поле «Входной интервал Х» необходимо
ввести массив факторных признаков (ячейки факторных признаков должны быть
все заполнены). Следует проследить, чтобы в поле «Уровень наде

176
«Новый рабочий лист». Можно задать Выходной интервал на выбранном рабо-
чем листе произвольно. Результаты для рассмотренного выше примера приведе-
ны на рис. 6.3.8.
Таблица регрессионной статистики
Множественный R – совокупный коэффициент корреляции. Чем ближе
данн
т обеспечивает информацией о том, какое значе-
ние можно было бы получить в другом наборе данных, который б о
больше, чем а нном случае. Пр юдений
больше 100 нормированны
ижен к фактическому R
2
. Формула для вы-
числения нормированного R
ый коэффициент к 1, тем больше оснований считать, что параметры регрес-
сионной модели отражают степень эффективности включенных в нее факторов.
R - квадрат – коэффициент детерминации, показывает, в какой мере вариа-
ция результативного признака объясняется включенными в модель ценообра-
зующими факторами.
Наблюдения – количество объектов, размер выборки.
Нормированный R
-квадра
ыл бы намног
нализируемый в да и количестве аблн
й R
2
прибл
2
имеет вид:
1
1
11
22
n-m-
n-
)- R-(R
норм.
= ,
где n – количество наблюдений, m – количество переменных (факторов).
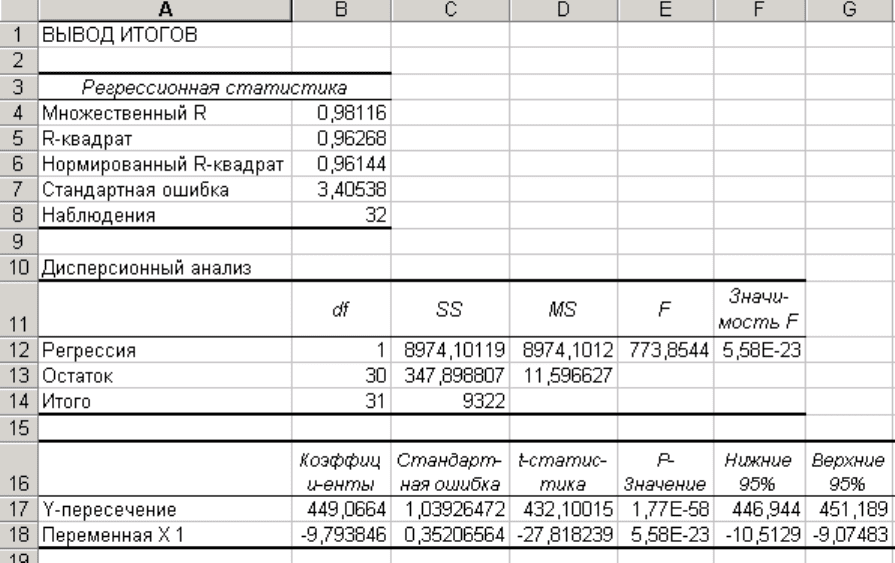
Рис. 6.3.8.
Стандартная ошибка – Sy, среднеквадратическое значение отклонения рег-
рессии от эмпирических данных.
Значение коэффициентов приведено во втором столбце «Коэффициенты»
следующей таблицы.
Стандартная ошибка – это стандартная погрешность коэффициентов. Если
разделить значение коэффициента на стандартную ошибку, то получится стан-
дартизированная, или нормированная переменная (t-статистика, приведенная в
четвертом столбце таблицы).
Р-значение – уровень значимости α
для значений t-статистики или вероят-
ность измерения доли коэффициента регрессии в его стандартной погрешности в
тех размерах, в которых она представлена, даже если коэффициент регрессии
фактически равен нулю. Находиться он должен по формуле = СТЬЮДРАСП(t-
стат 2).
того, что коэффициент
примет
нулевое значение. Это может свидетельствовать о бесполезности данного
коэффициента (за исключением Y - пересечения, оно может быть больше или
истика; число степеней свободы;
Чем больше значение P, тем больше вероятность
177

178
равн
вами, если введенный
в модель фактор может принять нулевое значение,
то его ельно и его следует уб-
рать и
сегда на единицу
меньше, чем параметров переменной.
Использование фиктивных переменных в значительной сте т
сферу применения и и. Они озволяю ка-
ционные переменны ри ычислять вклад к ре-
мен тативн й призн даже если между критериями нет линейной
свя
е переменные еют ситуации, а зна-
чен
ько на переменная у . Двоичные пере-
мен тся причин бкос и и мог ать чис-
лен ни актери к, ко с являются коли-
чес мер . табл. 6.3.4.) К и улевой помога-
тел ой ницу к между ной си-
туа
уровнем.
Таблица 6.3.4.
то помеще
о 0). В данном примере вероятность принятия переменными нулевого зна-
чения мала.
Для каждого коэффициента приводится доверительный интервал (нижнее
95%; верхнее 95%). Если в данный интервал попадает нулевое значение, то дан-
ный коэффициент не значим. Необходимо добиться результата, чтобы коэффи-
циенты регрессии с вероятностью 95% не принимали нулевых значений. Други-
ми сло
влияние на результативную переменную сомнит
з модели, после чего следует заново рассчитать все параметры уравнения.
Для построения уравнения регрессии с нечисловыми переменными, рекомен-
дуется ввести в уравнение фиктивные переменные, количество фиктивных пере-
менных в
пени расширяе
регресс
е на к
онной модел
терии и в
п т ввод
аждог
ить классифи
о критерия пе
ной в резуль ы ак (
зи).
Все фиктивны им значение 0 для базовой
ие
1 имеет тол
од для каждой сит ации
ные использую по е ги ти их применен я. Он ут д
ное представле е хар сти торые по своей ути не
твенными (при см оэффициент пр нен вс
ьной переменн определяет раз в значении фун ции дан
цией и
базовым
Сос яние ния
Фактор значе
x
ы и их ния
x
1 2
Отличное 0 1
Хорошее 1 0
Состояние помеще
Удовл рител 0
ния
етво ьное 0

179
Напри дная группа объектов: двухкомнатные квартиры на
Моск
площа . Выбранные квартиры имеют
разли
от сос е-
менны
мер, выбрана одноро
овском пр., удаленность от станции метро до 5 минут, в сталинском доме,
дь кухни от 8 до 13 кв. м, не крайние этажи
чную отделку помещения. Найдем уравнение регрессии стоимости 1 кв. м.
тояния помещения. В таблице указаны значения вспомогательных пер
х, которые
вводятся в уравнение регрессии:
i
n
i
i
xY
∑
=
где Y – результативный признак, например, Y=P
, где P – цена 1 кв. м; x - i-й не-
мый (ценообразующий) фактор; β
i
– коэффициент при x
i
.
В данном примере коэффициент α - это стоимость 1 кв. м о -
вой ситуации, коэффициент x
1
означает состо при-
рост стоимости 1 кв. м, значению β
фициен чает,
что отличное состояние прибавляет к стоимо . м вели
6.3.5.
Состояние
β+α=
1
,
s s i
зависи
бъекта для базо
β
1
при , что хорошее яние дает
равный
1
, а коэф т β
2
при x
2
озна
сти 1 кв чину β
2
.
Таблица
помещения
Адрес
Цена 1 кв.м.,
х
1
$
х
2
Московский пр., 191 459 0 0
Московский пр., 193 469 0 0
Московский пр., 216 470 0 0
Московский пр., 216 473 1 0
Московский пр., 218 475 1 0
Московский пр., 191 479 1 0
Московский пр., 195 487 0 1
Московский 489 0 пр., 194 1
М 491 0 1 осковский пр, 194
Результат анализа:
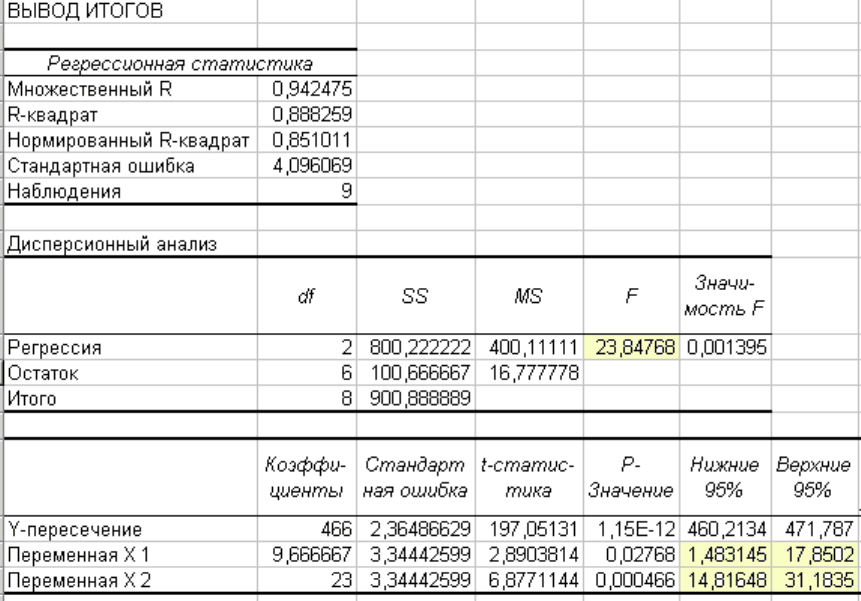
F
F
7,85), β
2
(14,82
ртиры для данного сег-
мента дующим образом: P
s
=466+10x
1
+23x
2
. То есть, отличное
состояние добавляет к стоимости квартиры ~$23, хорошее ~ $5, что может быть
использовано ом под-
ходе.
етодом массовой оценки определите стоимость 1 кв. м общей площади
торгово нные в
табли
крит
.= FРАСПОБР(0,05;2;6)=5,14
расч
=23,85 > F
крит
.=5,14; следовательно, R
2
значим.
Доверительные интервалы для коэффициентов уравнения: β
1
(1,48-1
-31,18) не содержат нулевое значение и проходят проверку на значимость.
Следовательно, зависимость цены от состояния ква
, можно описать сле
в качестве компенсационных корректировок в сравнительн
Задание 1. Определение регрессионного уравнения
М
го центра, если имеются данные об объектах-аналогах, представле
це 6.3.6. Постройте уравнение регрессии и рассчитайте
стоимость объекта
оценки.
180
