Pumping Station Desing - Second Edition by Robert L. Sanks, George Tchobahoglous, Garr M. Jones
Подождите немного. Документ загружается.

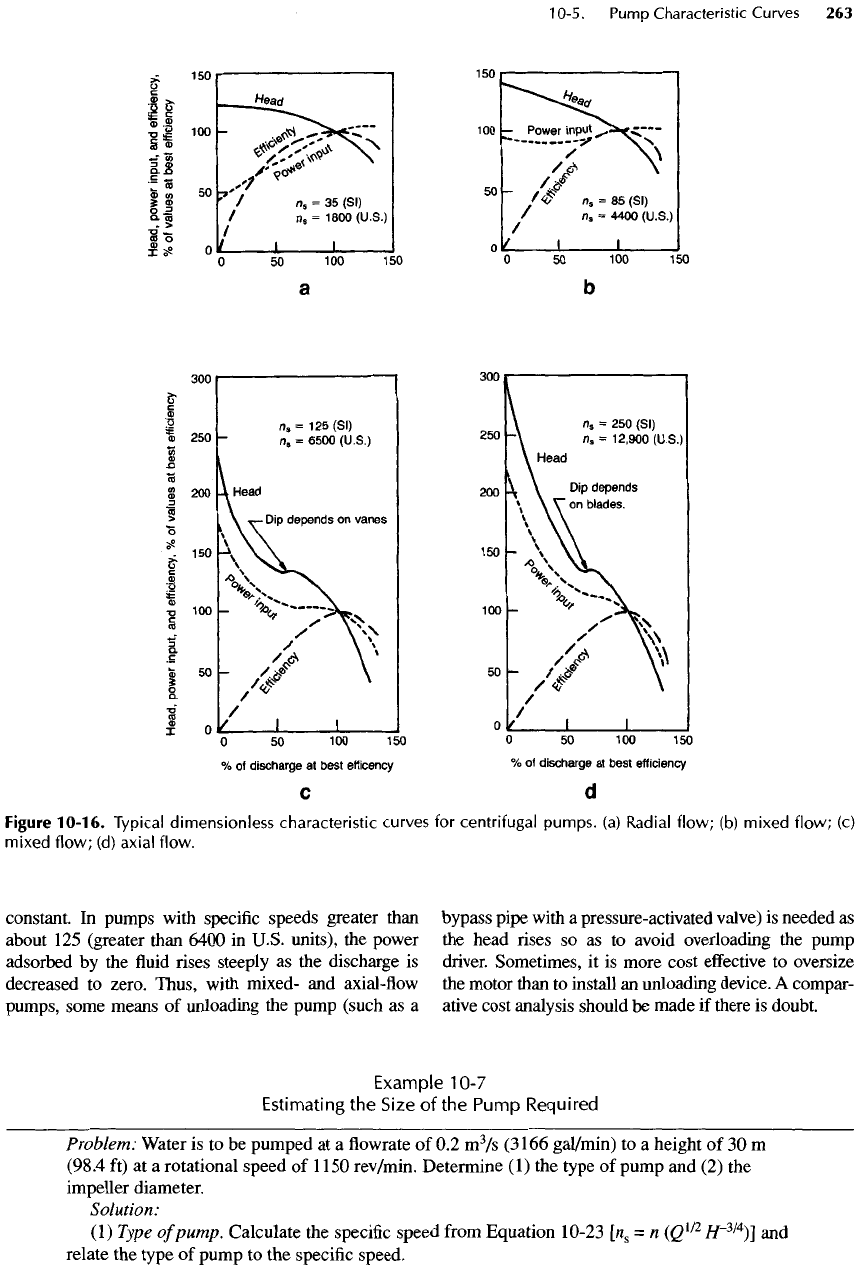
constant.
In
pumps with specific speeds greater than
about
125
(greater than
6400
in
U.S. units),
the
power
adsorbed
by the fluid
rises steeply
as the
discharge
is
decreased
to
zero. Thus, with mixed-
and
axial-flow
pumps,
some means
of
unloading
the
pump (such
as a
bypass pipe with
a
pressure-activated valve)
is
needed
as
the
head
rises so as to
avoid overloading
the
pump
driver.
Sometimes,
it is
more cost
effective
to
oversize
the
motor than
to
install
an
unloading device.
A
compar-
ative
cost analysis should
be
made
if
there
is
doubt.
Figure
10-16.
Typical dimensionless characteristic curves
for
centrifugal
pumps,
(a)
Radial
flow;
(b)
mixed
flow;
(c)
mixed
flow;
(d)
axial
flow.
Example
10-7
Estimating
the
Size
of the
Pump
Required
Problem: Water
is to be
pumped
at a flowrate of 0.2
m
3
/s
(3166
gal/min)
to a
height
of 30
m
(98.4
ft) at a
rotational speed
of
1150
rev/min.
Determine
(1)
the
type
of
pump
and (2) the
impeller diameter.
Solution:
(1)
Type
of
pump.
Calculate
the
specific
speed
from
Equation 10-23
[n
s
= n
(Q
l/2
/T
3/4
)]
and
relate
the
type
of
pump
to the
specific speed.
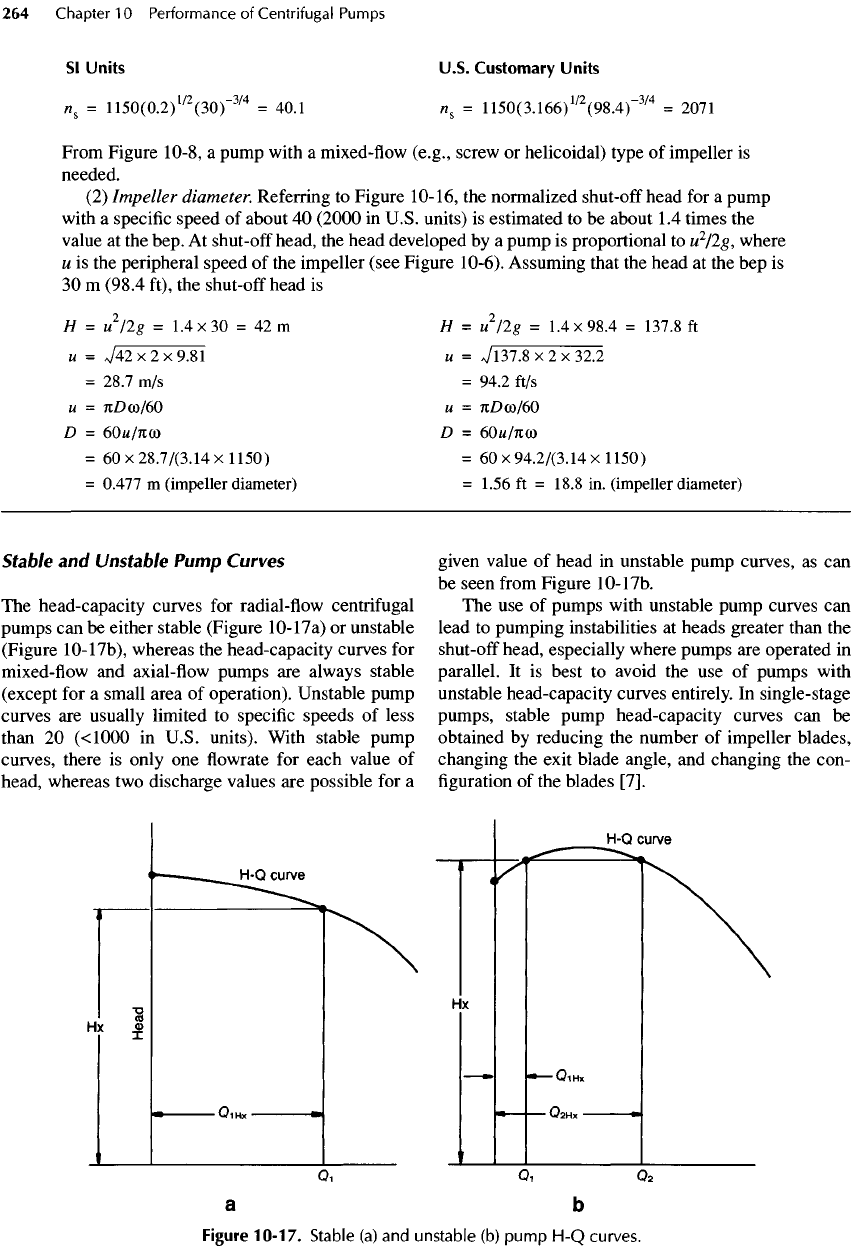
Stable
and
Unstable
Pump
Curves
The
head-capacity curves
for
radial-flow
centrifugal
pumps
can be
either stable (Figure
10-17a)
or
unstable
(Figure
10-17b),
whereas
the
head-capacity curves
for
mixed-flow
and
axial-flow
pumps
are
always stable
(except
for a
small area
of
operation). Unstable pump
curves
are
usually limited
to
specific
speeds
of
less
than
20
(<1000
in
U.S. units). With stable pump
curves,
there
is
only
one flowrate for
each value
of
head, whereas
two
discharge values
are
possible
for a
given
value
of
head
in
unstable pump curves,
as can
be
seen
from
Figure
10-17b.
The use of
pumps with unstable pump curves
can
lead
to
pumping instabilities
at
heads greater than
the
shut-off
head, especially where pumps
are
operated
in
parallel.
It is
best
to
avoid
the use of
pumps with
unstable
head-capacity curves entirely.
In
single-stage
pumps,
stable pump head-capacity curves
can be
obtained
by
reducing
the
number
of
impeller blades,
changing
the
exit blade angle,
and
changing
the
con-
figuration
of
the
blades
[7].
Figure
10-17.
Stable
(a) and
unstable
(b)
pump
H-Q
curves.
Sl
Units
U.S. Customary
Units
w
s
=
1150(0.2)
1/2
(30)~
3/4
=
40.1
/i
s
=
1150(3.166)
1/2
(98.4)~
3/4
=
2071
From Figure 10-8,
a
pump with
a
mixed-flow
(e.g., screw
or
helicoidal) type
of
impeller
is
needed.
(2)
Impeller diameter. Referring
to
Figure
10-16,
the
normalized
shut-off
head
for a
pump
with
a
specific speed
of
about
40
(2000
in
U.S. units)
is
estimated
to be
about
1.4
times
the
value
at the
bep.
At
shut-off
head,
the
head developed
by a
pump
is
proportional
to
u
2
/2g,
where
u
is the
peripheral speed
of the
impeller (see Figure 10-6). Assuming that
the
head
at the bep is
30 m
(98.4 ft),
the
shut-off
head
is
H
=
u
2
/2g
=
1.4x30
=
42m
H =
u
2
/2g
=
1.4x98.4
=
137.8ft
M
=
V42x2x9.81
u =
V137.8
x
2x32.2
=
28.7
m/s =
94.2 ft/s
u
=
nD
co/60
u = rcZ)co/60
D =
60M/71CO
D =
60w/7ico
=
60x28.77(3.14x1150)
=
60x94.27(3.14x1150)
=
0.477
m
(impeller
diameter)
=
1.56ft
=
18.8
in.
(impeller
diameter)
10-6.
Pump
Operating
Ranges
A
pump operates best
at its
best
efficiency
point.
Not
only
is the
efficiency
maximum,
but
radial loads
on the
impeller
and the
problems
of
cavitation
are
minimized.
It
is
good practice
to
limit
the
operating range
of
pumps
—
especially
radial-flow centrifugal
pumps
—
to
within
approximately +20%
and
-40%
of the
dis-
charge
at the
bep.
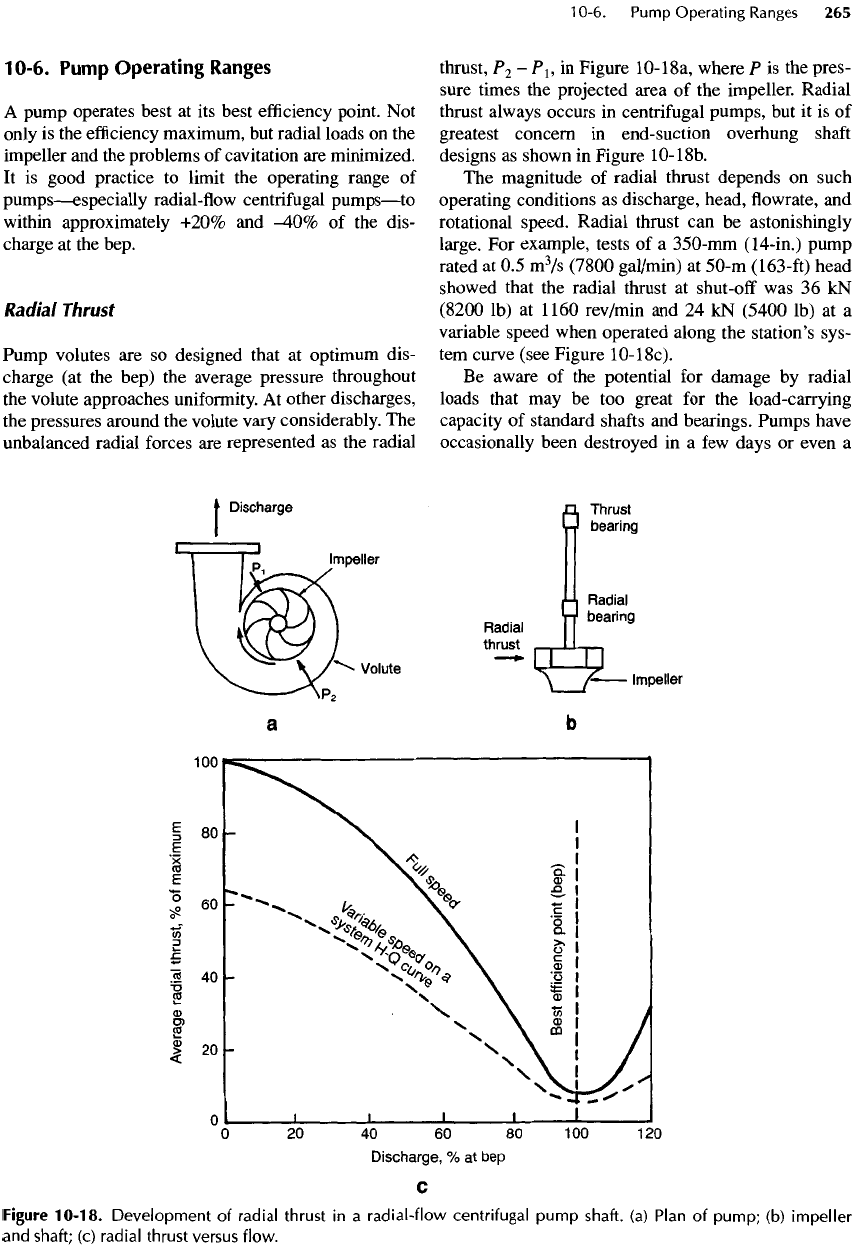
Radial Thrust
Pump
volutes
are so
designed that
at
optimum dis-
charge
(at the
bep)
the
average pressure throughout
the
volute approaches uniformity.
At
other discharges,
the
pressures around
the
volute vary considerably.
The
unbalanced
radial forces
are
represented
as the
radial
thrust,
P
2
-
PI,
in
Figure
10-18a,
where
P is the
pres-
sure
times
the
projected area
of the
impeller. Radial
thrust
always occurs
in
centrifugal pumps,
but it is of
greatest concern
in
end-suction overhung
shaft
designs
as
shown
in
Figure
10-18b.
The
magnitude
of
radial thrust depends
on
such
operating conditions
as
discharge, head,
flowrate, and
rotational speed. Radial thrust
can be
astonishingly
large.
For
example, tests
of a
350-mm
(14-in.)
pump
rated
at 0.5
m
3
/s
(7800
gal/min)
at
50-m
(163-ft)
head
showed that
the
radial thrust
at
shut-off
was 36
kN
(8200
Ib)
at
1160 rev/min
and 24 kN
(5400
Ib)
at a
variable speed when operated along
the
station's sys-
tem
curve (see Figure
10-18c).
Be
aware
of the
potential
for
damage
by
radial
loads that
may be too
great
for the
load-carrying
capacity
of
standard shafts
and
bearings. Pumps have
occasionally been destroyed
in a few
days
or
even
a
Figure
10-18.
Development
of
radial
thrust
in a
radial-flow
centrifugal
pump
shaft,
(a)
Plan
of
pump;
(b)
impeller
and
shaft;
(c)
radial
thrust versus
flow.
few
hours through excessive wear
in
bearings, seals,
shaft
sleeves,
and
wearing
rings.
Bearings,
shafts,
and
casings must
be
designed
to
resist
the
anticipated
radial
loads (which
can be
approximated
by the
method given
by the
Hydraulic Institute
[I]).
Standard
pumps
can
often
be
customized with larger
shafts
and
bearings.
One
practical means
of
dealing with radial
thrust
is to
define
several critical operating points
and
require
the
manufacturer
to
furnish
a
pump with
a
specified
life
at
such points (see Appendix
C).
Cavitation
When
the
pump discharge rate increases beyond
the
best
efficiency
capacity
(bee),
the
absolute pressure
required
to
prevent cavitation increases
so
that cavita-
tion
is a
potential problem.
The
NPSH
R
curves
are the
basis
for
selecting
the
maximum permissible dis-
charge. When
the
pump discharge rate decreases
toward
zero
at the
shut-off
head,
the
radial load
increases
and the
recirculation
of the
pumped
fluid
within
the
impeller becomes
a
problem. This recircu-
lation
can
cause vibration
and may
also result
in
cavi-
tation
that
can
ruin
the
impeller.
Pumps
should
not be
operated
at or
near
the
shut-off
head
for
extended periods
of
time because
such
operation also leads
to
heating
of the
liquid
and
can
cause severe wearing-ring
rub and
other
problems.
Fixed
Efficiency
Loss
For a
given impeller diameter,
the
operating range
of a
pump
can be
established
by (1)
setting
a
limit
on the
minimum
acceptable
efficiency
and (2)
setting upper
and
lower limits
on the
allowable speed changes.
Alternatively,
if the
diameter
of the
pump impeller
is
to be
changed,
the
operating range
of the
pump
can be
established
by (1)
setting
a
limit
on the
minimum
acceptable
efficiency
and (2)
setting upper
and
lower
limits
on the
allowable impeller diameters.
The
operating range
of a
pump based
on
these cri-
teria
is
illustrated
in
Figure
10-19.
Percentage
of
Capacity
An
alternative approach used
to
establish
the
pump
operating range
is to set
limits
on the
pump discharge
as
a
percentage
of the
bee.
An
operating range
of 60 to
120%
of the
bee
is
often
recommended
for
pumps with
specific
speeds less than
40
(<2000
in
U.S. units)
[16].
Pump
operating envelopes
are
defined
using these val-
ues,
as
illustrated
in
Figure 10-20,
for
changes
in
speed
as
well
as for
changes
in the
impeller diameter.
1
0-7.
Elementary
Pump
System
Analysis
In
any
pump-force
main system,
the
head developed
by
the
pump must equal
the
total dynamic headloss
in
Figure
10-19.
Pump
operating
envelopes based
on a
fixed efficiency
loss,
(a)
Change
of
rotational
speed;
(b)
change
of
impeller
diameter.
the
system, and,
of
course,
the
discharge
in
pump
and
pipe
are
equal. This relationship determines
the
"pump
operating point,"
a
single point
on
both
the H-
Q
curve
of the
pump
and the H-Q
curve
of the
piping
system.
There
are
several ways
of
finding
the
pump
operating point, including computer analysis
and
sev-
eral graphical methods,
but the
simplest
(for simple
problems)
and the
most universally used method
is
given
in
this section.
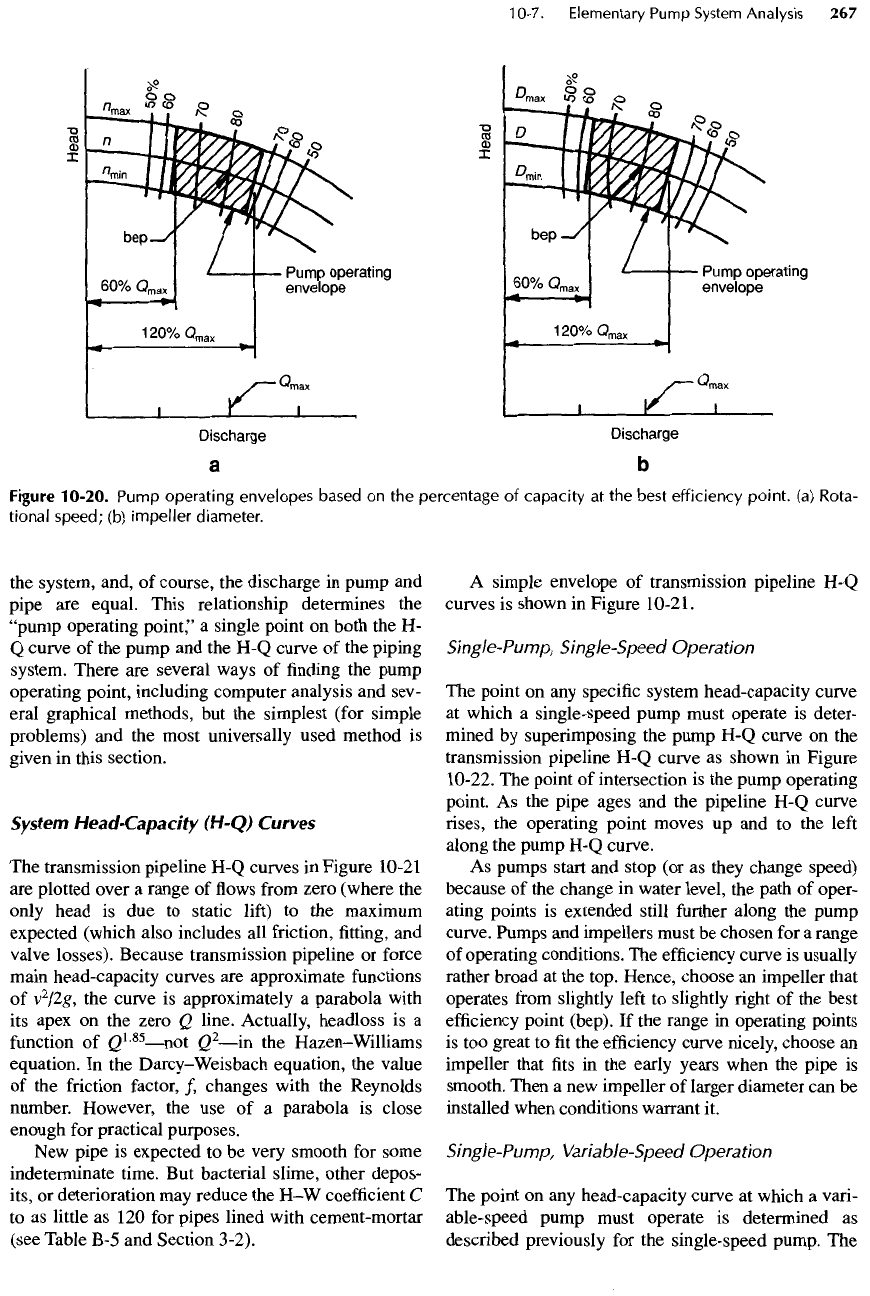
System
Head-Capacity
(H-Q)
Curves
The
transmission pipeline
H-Q
curves
in
Figure 10-21
are
plotted over
a
range
of flows
from
zero (where
the
only head
is due to
static
lift)
to the
maximum
expected (which also includes
all
friction,
fitting,
and
valve
losses). Because transmission pipeline
or
force
main head-capacity curves
are
approximate functions
of
v
2
/2g,
the
curve
is
approximately
a
parabola with
its
apex
on the
zero
Q
line. Actually, headloss
is a
function
of
Q
LS5
—
not
Q
2
—
in
the
Hazen-Williams
equation.
In the
Darcy-Weisbach equation,
the
value
of
the
friction
factor,
/,
changes with
the
Reynolds
number. However,
the use of a
parabola
is
close
enough
for
practical purposes.
New
pipe
is
expected
to be
very smooth
for
some
indeterminate time.
But
bacterial
slime, other depos-
its,
or
deterioration
may
reduce
the H-W
coefficient
C
to
as
little
as
120
for
pipes lined with cement-mortar
(see Table
B-5 and
Section 3-2).
A
simple envelope
of
transmission pipeline
H-Q
curves
is
shown
in
Figure
10-21.
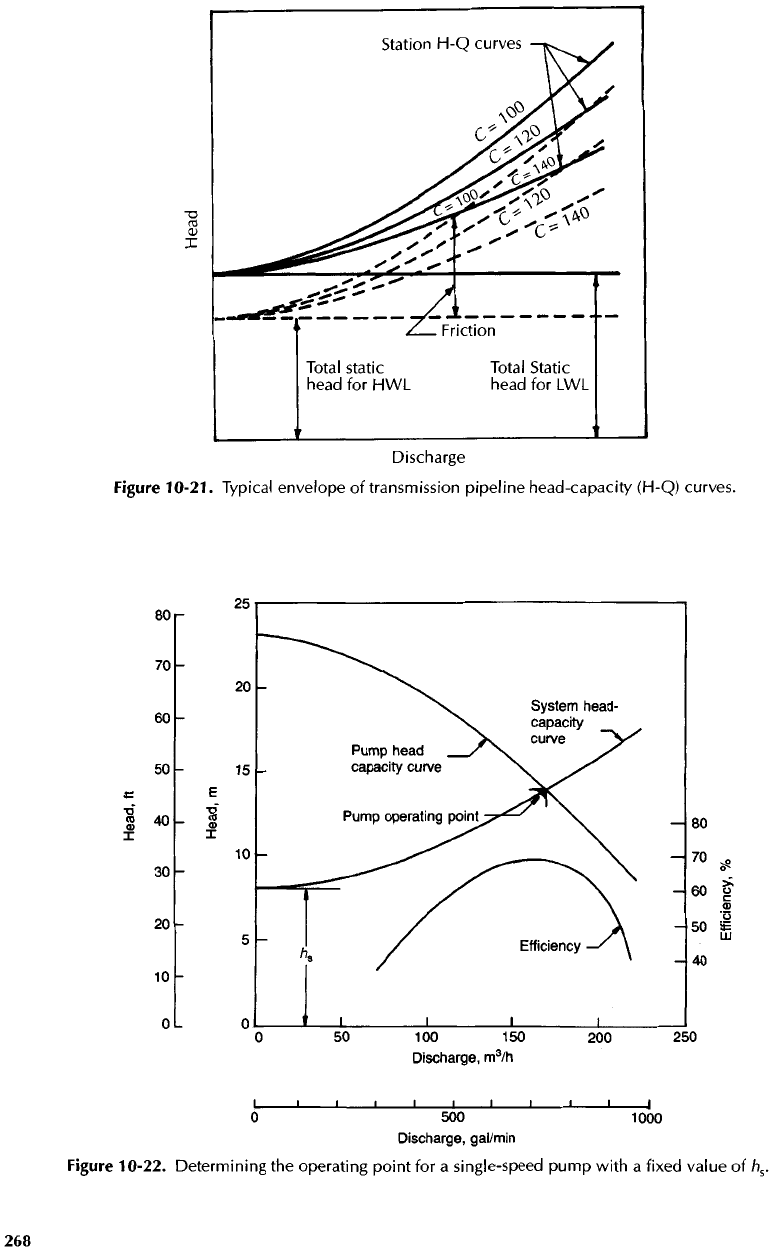
Single-Pump,
Single-Speed
Operation
The
point
on any
specific
system head-capacity curve
at
which
a
single-speed
pump must
operate
is
deter-
mined
by
superimposing
the
pump
H-Q
curve
on the
transmission pipeline
H-Q
curve
as
shown
in
Figure
10-22.
The
point
of
intersection
is the
pump operating
point.
As the
pipe ages
and the
pipeline
H-Q
curve
rises, the
operating point moves
up and to the
left
along
the
pump
H-Q
curve.
As
pumps start
and
stop
(or as
they change speed)
because
of the
change
in
water level,
the
path
of
oper-
ating points
is
extended still
further
along
the
pump
curve. Pumps
and
impellers must
be
chosen
for a
range
of
operating conditions.
The
efficiency
curve
is
usually
rather broad
at the
top. Hence, choose
an
impeller that
operates
from
slightly
left
to
slightly
right of the
best
efficiency
point (bep).
If the
range
in
operating points
is too
great
to fit the
efficiency
curve nicely, choose
an
impeller
that
fits in the
early years when
the
pipe
is
smooth. Then
a new
impeller
of
larger diameter
can be
installed
when conditions warrant
it.
Single-Pump,
Variable-Speed
Operation
The
point
on any
head-capacity curve
at
which
a
vari-
able-speed pump must operate
is
determined
as
described previously
for the
single-speed pump.
The
Figure
10-20.
Pump
operating
envelopes based
on the
percentage
of
capacity
at the
best efficiency
point,
(a)
Rota-
tional
speed;
(b)
impeller
diameter.
Figure
10-21. Typical envelope
of
transmission
pipeline
head-capacity (H-Q) curves.
Figure
10-22. Determining
the
operating
point
for a
single-speed pump
with
a
fixed value
of
h
s
.

Multiple
Pump
Operation
In
pumping stations where several pumps
are
installed,
two or
more pumps
are
usually operated
in
parallel. Occasionally, pumps
are
operated
in
series.
The
elements
of the
methods used
to
develop
the
combined
H-Q
curve
for
multiple pumps
are
outlined
in the
following subsections.
A
more
extensive explanation
for
multiple pumps
is
given
in
Section 10-8.
Parallel
Operation
When
two or
more pumps
are
discharging into
the
same header
or
manifold,
the
total
flow is
found
by
adding
the
individual
flows at a
given head.
A
correc-
tion (usually small) must
be
made, however, because
the
higher
flow
causes higher headlosses that slightly
reduce
the flow
either pump would discharge
if
oper-
ated alone.
One
method
for
combining
the flows is to
subtract
from
the
pump curve those station headlosses
in
the
suction
and
discharge piping
up to the
intersec-
affinity
laws
are
used,
as
shown
in
Example 10-8,
to
determine
the
rotational speed
at any
other desired
operating point
on the
system curve. Again,
the
oper-
ating point moves along
the
pump
H-Q
curve,
although
not so
far, because
the
change between
HWL
and
LWL is
less than with single-speed operation.
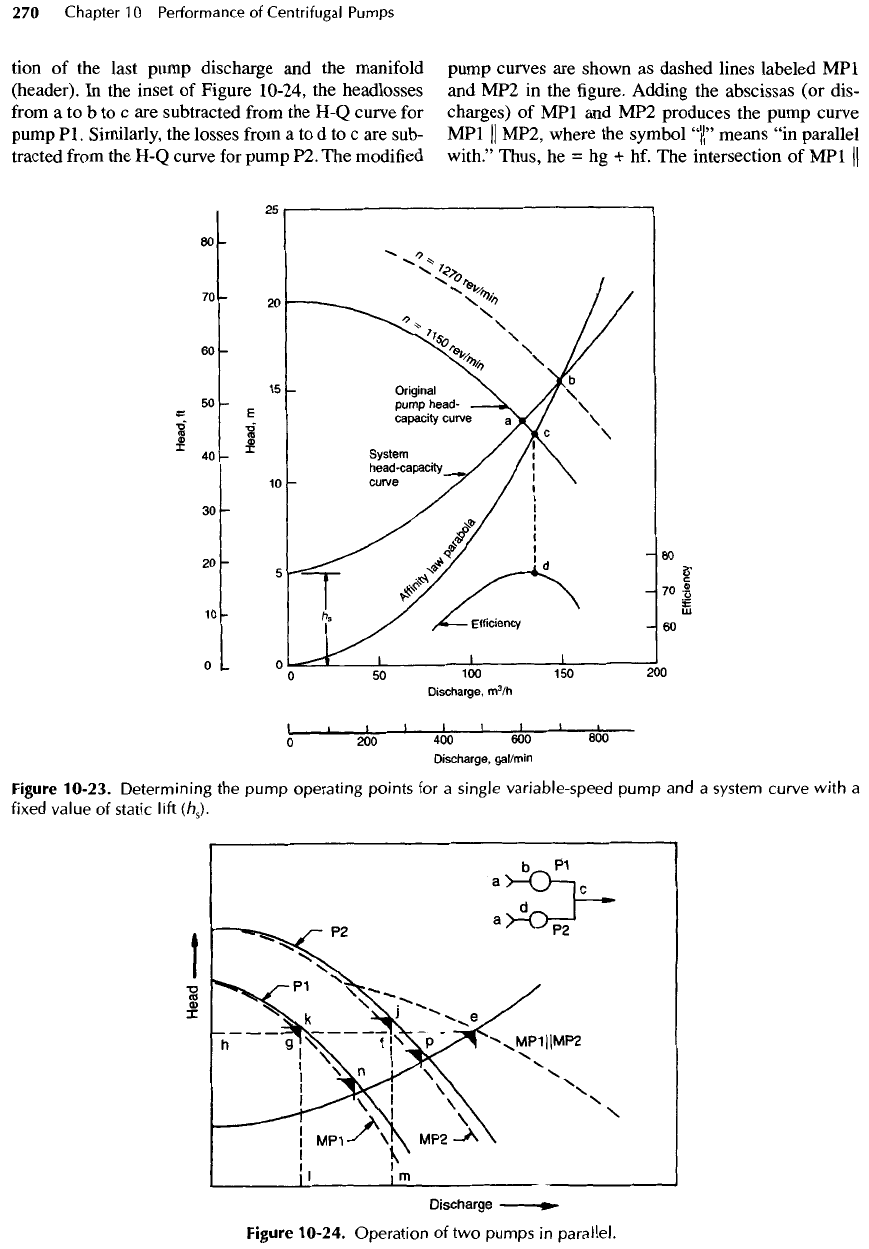
Example
10-8
Application
of a
Variable-Speed Pump
Problem:
The
pump curve shown
in
Figure 10-23
is for a
pump operated
at
1150
rev/min
that
pumps
130
m
3
/h
(572
gal/min)
at a
head
of
13.2
m
(43.3 ft), which
is
shown
as
point
a. If the
pump
must discharge
150
m
3
/h
(660 gal/min)
at a
head
of
15.5
m
(50.8 ft), which
is
shown
as
point
b,
what
is (1) the
required
new
operating speed
and (2) the
efficiency
of the new
operating
point?
Solution:
(1)
Operating
speed. Extend
the
system
H-Q
curve
from
point
a to an
intersection
with
the
desired
flowrate at
point
b. The new
pump curve must pass through point
b.
Note that
Equation 10-15
(QJQ
2
=
K
1
In
2
)
cannot
be
used
to find the
pump speed because points
a and b
are not
corresponding points (see Example 10-2
and the
text following Equation
10-17).
One
way
to
solve
the
problem
is to
create
an
"affinity
law
parabola"
by
solving Equations
10-15
and
10-16
simultaneously
to
eliminate
m
/QA
2
fn
}
\
2
H
}
2
(W
=
(^
-^
"'
=
//2(Gi/22)
which
defines
a
parabola passing through
the
origin
and
point
b in
Figure 10-23. Every point
on
the
parabola
is a
corresponding point. Because point
b
corresponds
to
point
c,
Equation 10-15
can
be
used
to find
speed
at
point
b
after
Q is
scaled
at
point
c.
Sl
Units
U.S. Customary
Units
Q
c
=
136
m
3
/h
(by
scaling)
Q
c
= 598
gal/min
(by
scaling)
From Equation
10-15
(/i
b
=
n
c
CyQ
0
),
n
b
=
1150(150/136)
=
1270
rev/min
n
b
=
1150(660/598)
=
1270
rev/min
By
scaling
H at
points
b and c, the
speed
can
also
be
found
from
Equation
10-16
(n
b
=
njH
b
/H
c
).
n
b
=
1150V15.4/12.6
=
1270
rev/min
n
b
=
1150^50.5/41.3
= 270
rev/min
(2)
Efficiency.
The
efficiency
of the new
operating point
is
found
by
projecting
a
line
from
point
c
downward
to
point
d on the
efficiency
curve, which gives
an
expected
efficiency
of
75%.
tion
of the
last pump discharge
and the
manifold
(header).
In the
inset
of
Figure 10-24,
the
headlosses
from
a to b to c are
subtracted
from
the H-Q
curve
for
pump
Pl.
Similarly,
the
losses
from
a to d to c are
sub-
tracted
from
the H-Q
curve
for
pump
P2. The
modified
pump
curves
are
shown
as
dashed lines labeled
MPl
and
MP2 in the figure.
Adding
the
abscissas
(or
dis-
charges)
of MPl and MP2
produces
the
pump curve
MPl
Il
MP2, where
the
symbol
"||"
means
"in
parallel
with." Thus,
he = hg + hf. The
intersection
of MPl ||
Figure
10-23.
Determining
the
pump
operating
points
for a
single variable-speed
pump
and a
system curve
with
a
fixed value
of
static
lift
(h
s
).
Figure
10-24.
Operation
of two
pumps
in
parallel.
MP2
with
the
system curve
for the
manifold
and
force
main
downstream
from
point
c is the
operating point
(point
e) for the
pumps when both
are
running.
To
find the
discharge contributed
by
each pump,
draw
the
horizontal line,
eh,
which intersects
the
mod-
ified
pump curves
at f and g. The
discharge
from
Pl is
hg;
from
P2 it is hf. To find the
total head
at
which
each individual pump operates, project
a
vertical line
from
f to j and
from
g to k. The
actual operating point
of
Pl is
point
k and the
head
on the
pump
is
kl.
The
operating point
of P2 is
point
j and the
head
is jm.
With
one
pump off,
the
other operates
at
point
n
(for
Pl)
or
point
p for P2. The
pump specifications must
be
written
for
pump
Pl
operating either
at
point
k or
point
n and for
pump
P2 at
point
j or
point
p.
Series Operation
Pumps
are
operated
in
series,
as
shown
in
Figure
10-25,
when
the
head requirement
is
greater than
can
be
obtained with
a
single pump.
The
combined head
capacity curve,
Pl + P2, is
found
by
adding
ordi-
nates
—
that
is, the
heads developed
at the
same
dis-
charge. Thus,
ad = bd + cd. The
operating point
is
point
c for
pump
Pl and
point
b for
pump
P2, and the
operating point
for the
system
is
point
a.
10-8.
Practical Pumping System
H-Q
Curve
Analysis
The
fundamentals
of
pumping system analysis,
explained
in the
previous section, should
be
reviewed
before
reading this section,
in
which additional details
add
practicality
to
this subject.
The
ultimate objective
in
analyzing
a
pumping system
is to
describe
the
required range
of
operating conditions
in
sufficient
detail
to be
able
to (1)
understand
the
application
yourself,
and (2)
with that understanding, describe
the
application
to
equipment suppliers
in
sufficient
detail
that
they
may
intelligently apply their products.
With
these objectives
in
mind,
the
full
range
of
operating conditions must
be
examined
to
develop
a
complete understanding
of the
application. Constant
speed
(C/S)
and
variable speed
(V/S)
pumps
are
con-
sidered separately
in the
following discussion.
Constant-Speed
(C/S)
Pumps
in
Parallel
A
typical schematic diagram
of a
pump
and
piping
system
for a
pumping station with
four
assumed
C/S
pumps
(one
a
standby) that discharge into
a
manifold
and
thence into
the
force main
is
shown
in
Figure
10-26.
The
system
is
divided into three basic compo-
nents
—
force
main, suction piping,
and
discharge
pip-
ing. Head-capacity
(H-Q)
curves
are
drawn
for
each
component.
The H-Q
curves
for the
pumps
are
then
superimposed. Collectively,
the
curves
are
called
"system
curves."
In
Figure 10-27, dynamic head
losses
in
suction
and
discharge piping
are
combined
into Curve
B + C.
Curves
A,
A',
and
A"
(usually
the first
ones drawn)
are
combinations
of
static head plus
the
dynamic head
losses
from
the
manifold
to the
point
of
discharge.
The
curves must encompass
the
entire envelope
of
Figure
10-25. Operation
of two
pumps
in
series.
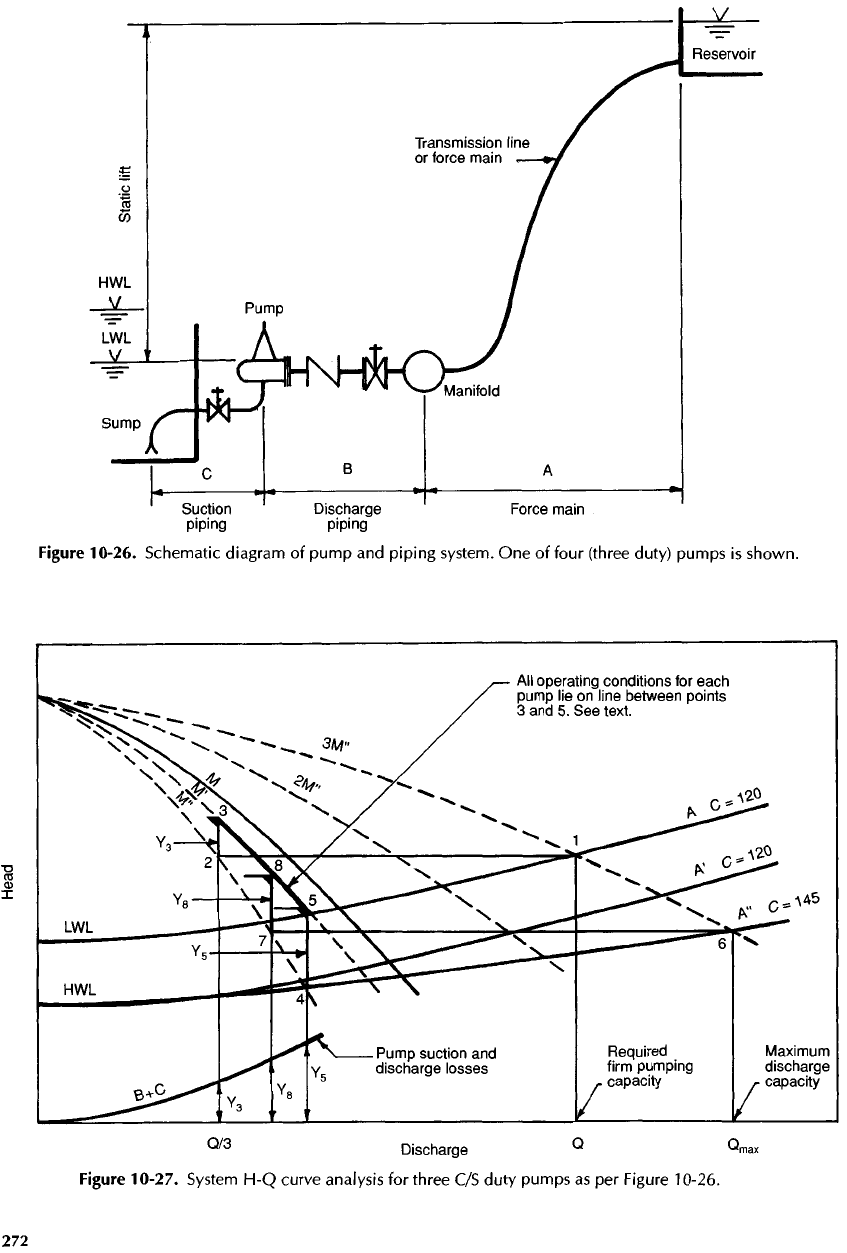
Figure
10-26. Schematic diagram
of
pump
and
piping
system.
One of
four (three duty) pumps
is
shown.
Figure
10-27.
System
H-Q
curve
analysis
for
three
C/S
duty pumps
as per
Figure
10-26.
