Презентация - Загиров Н.Н., Иванов Е.В. Механика сплошных сред. Теория обработки металлов давлением
Подождите немного. Документ загружается.


В матрице первый индекс по строкам фиксирован В матрице первый индекс по строкам фиксирован
и означает номер строки, и означает номер строки,
а второй а второй –– столбца. Для трех свободных индексов столбца. Для трех свободных индексов
число компонентов будет число компонентов будет 2727 и т. д. и т. д.
Величину Величину δδ
ijij
определяют равенствамиопределяют равенствами
≠
=
=δ
; при ,0
; при ,1
ji
ji
ij
называют симметричным символом Кронекера; называют симметричным символом Кронекера;
она образует квадратичную единичную матрицуона образует квадратичную единичную матрицу
Е
ij
=
δ
=
100
010
001
, , 1.11.1
, , 1.21.2

В векторном и тензорном исчислении В векторном и тензорном исчислении
встречаются характерные суммы, например,встречаются характерные суммы, например,
∑
=++=
=
z
xi
iizzyyxx
eaeaeaeaa
∑
=++=⋅
=
z
xi
iizzyyxx
bababababa
, , 1.31.3
, , 1.41.4

В подобных характерных суммах условились В подобных характерных суммах условились
знак опускать и ввели соглашение о суммировании: знак опускать и ввели соглашение о суммировании:
если подстрочные индексы если подстрочные индексы i, j, и т. д. Встречаются и т. д. Встречаются
дважды, то это означает сумму трех слагаемых, дважды, то это означает сумму трех слагаемых,
индексы каждого из которых фиксированы и индексы каждого из которых фиксированы и
равны соответственно равны соответственно x, y, z.
Повторяющиеся индексы Повторяющиеся индексы i, j и т. д., по которым и т. д., по которым
производится суммирование, называют немыми. производится суммирование, называют немыми.
В соответствии с этим выражения (В соответствии с этим выражения (1.31.3) и () и (1.41.4) )
могут быть записаны короче:могут быть записаны короче:
∑
=
z
xi
ii
eaa
=
ii
baba
=
⋅
, , 1.51.5
, , 1.61.6

Обратимся к единичным ортогональным векторам Обратимся к единичным ортогональным векторам
трехмерного пространства, исходящим из одной трехмерного пространства, исходящим из одной
точки. Нельзя с помощью двух из них получить точки. Нельзя с помощью двух из них получить
третий; при сложении не получится вектор, третий; при сложении не получится вектор,
перпендикулярный плоскости этих векторов, перпендикулярный плоскости этих векторов,
результирующий вектор останется в той же результирующий вектор останется в той же
плоскости. В этом случае говорят, что векторы плоскости. В этом случае говорят, что векторы
линейно независимы. Любой четвертый вектор, линейно независимы. Любой четвертый вектор,
например например , в трехмерном пространстве можно , в трехмерном пространстве можно
считать уже линейно зависимым, так как его можно считать уже линейно зависимым, так как его можно
выразить через выразить через с помощью операции умножения с помощью операции умножения
последних на скалярные величины, численно равные последних на скалярные величины, численно равные
проекциям вектора на координатные оси, и проекциям вектора на координатные оси, и
сложения результатов (сложения результатов (1.31.3).).
i
e
i
e
a
i
e
Существует более общее определение линейно Существует более общее определение линейно
зависимых и линейно независимых векторов: зависимых и линейно независимых векторов:
векторы векторы , , , …, , …, называют линейно называют линейно
зависимыми, если найдутся такие зависимыми, если найдутся такие
действительные числа действительные числа α, β, …, γ, чточто
a
b
c
0
=
γ
+
+
β
+
α
с
...
в
а
Пусть Пусть αα≠≠00, тогда выражение (, тогда выражение (1.71.7) примет вид) примет вид
c...ba
α
γ
α
β
−−−=
, , 1.1.77

Если равенство (Если равенство (1.71.7) выполняется только тогда, ) выполняется только тогда,
когда все числа когда все числа α, β, …, γ равны нулю, равны нулю,
то векторы то векторы , , , …, , …, называют линейно называют линейно
независимыми.независимыми.
Наибольшее число линейно независимых Наибольшее число линейно независимых
векторов определяет размерность пространства. векторов определяет размерность пространства.
Пространство с двумя линейно независимыми Пространство с двумя линейно независимыми
векторами векторами –– двумерное, двумерное,
с тремя с тремя –– трехмерное.трехмерное.
Совокупность линейно независимых векторов, Совокупность линейно независимых векторов,
число которых равно размерности линейного число которых равно размерности линейного
пространства, можно принять за базиспространства, можно принять за базис
пространства.пространства.
a
b
c
Базис, состоящий из взаимно ортогональных Базис, состоящий из взаимно ортогональных
единичных векторов, называютединичных векторов, называют
ортонормированным ортонормированным
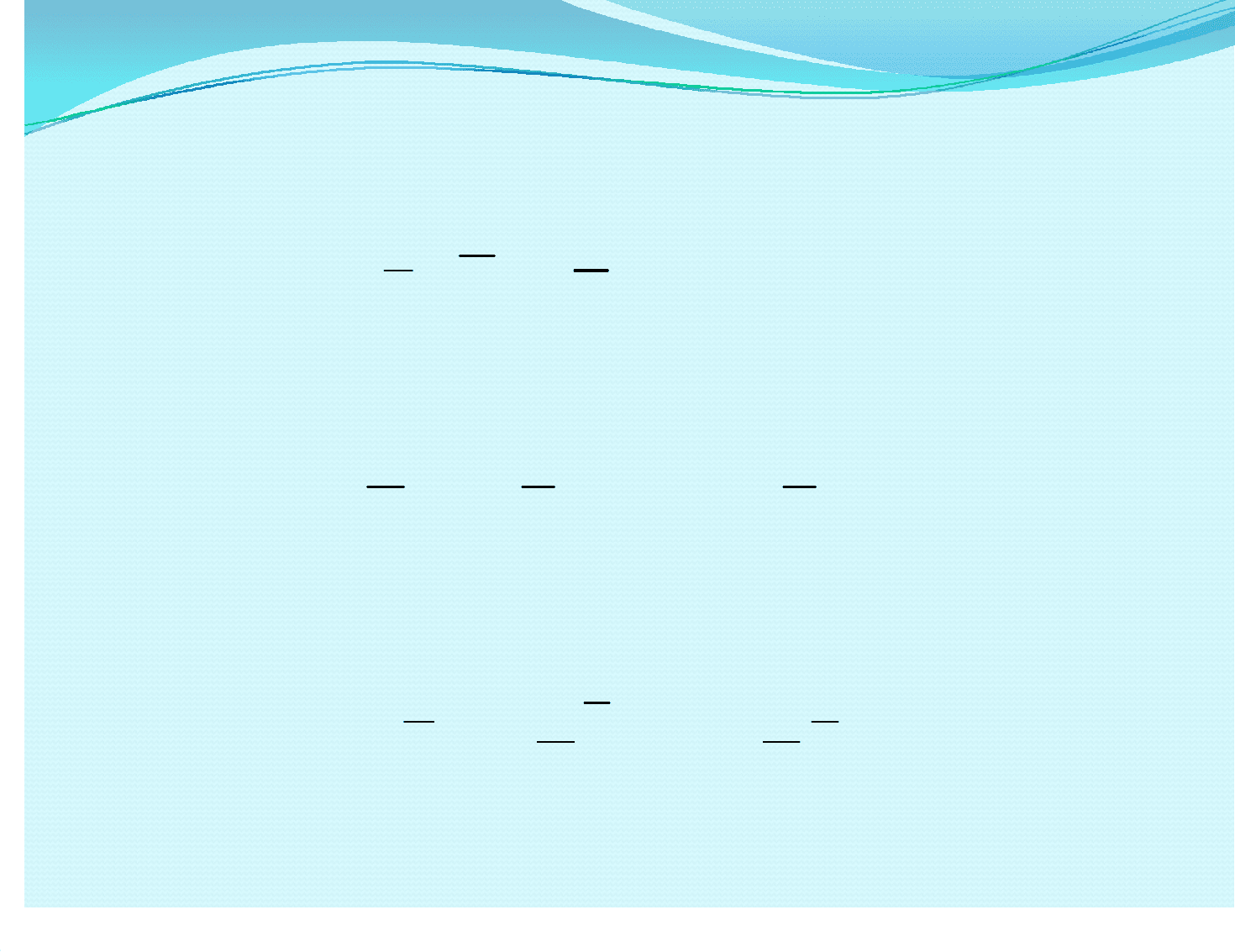
,zzyyxx
eaeaeaa
+
+
=
где где ,, , , -- вектора базиса; вектора базиса;
а
x
, a
y
, a
z
–– прямоугольные координаты вектора .прямоугольные координаты вектора .
x
e
y
e
z
e
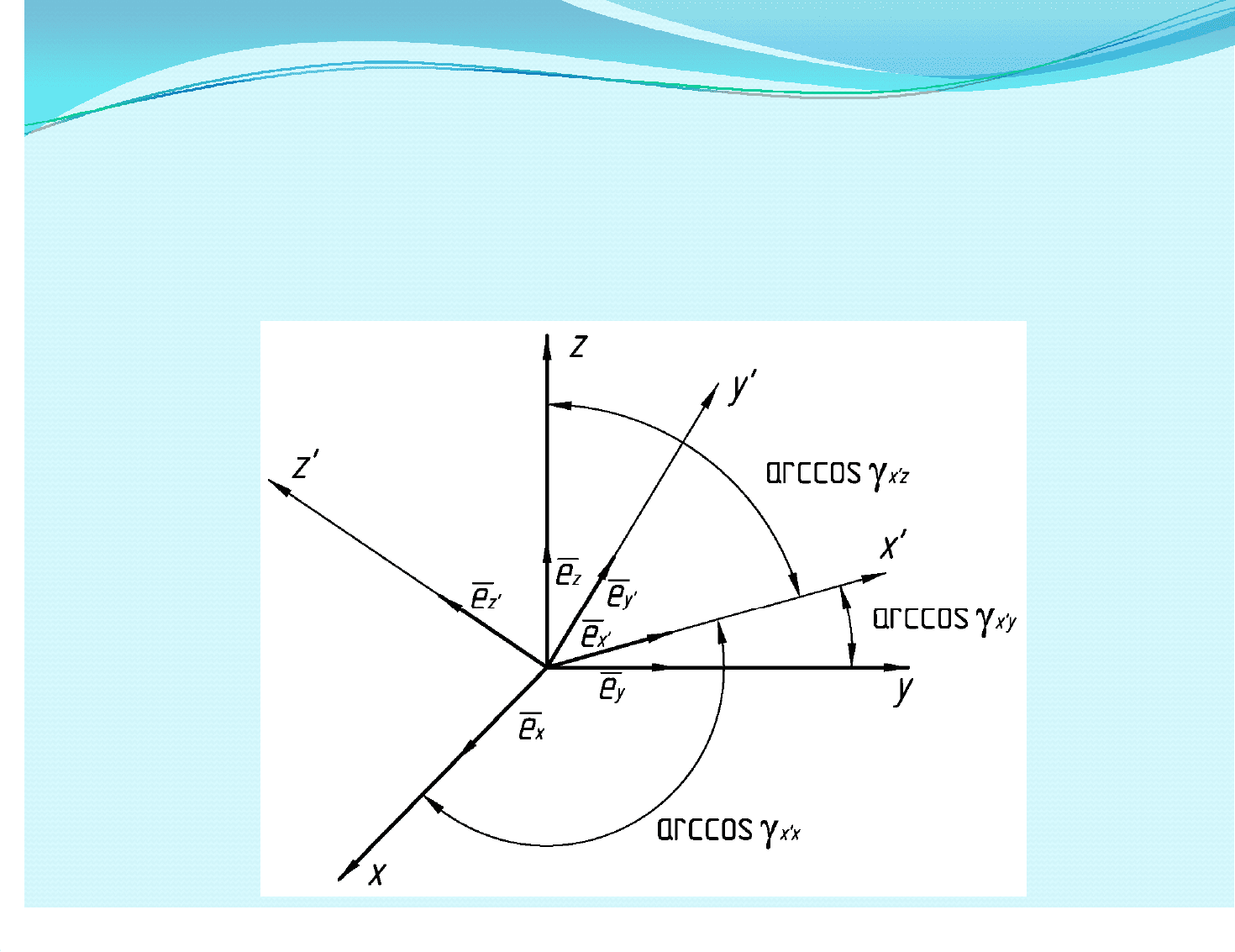
Рассмотрим преобразование Рассмотрим преобразование
ортонормированного базиса или системы ортонормированного базиса или системы
координат. Пусть в трехмерном пространстве координат. Пусть в трехмерном пространстве
наряду с ортонормированным базисом задан наряду с ортонормированным базисом задан
другой (новый) базис другой (новый) базис (i’ = x’, y’, z’).

Каждый из трех векторов нового базиса Каждый из трех векторов нового базиса
разложим по векторам старого базиса:разложим по векторам старого базиса:
ix'izx'zyx'yxx'xx'
еееее · = · + · +· =
γ
γ
γ
γ
iy'izy'zyy'yxy'xy'
еееее · = · + · +· =
γ
γ
γ
γ
iz'izz'zyz'yxz'xz'
еееее · = · + · +· =
γ
γ
γ
γ
где где γγ
ii’’ii
–– проекции векторов нового базиса на проекции векторов нового базиса на
старый.старый.
'i
e
, , 1.1.88

Поскольку проецируются единичные векторы, Поскольку проецируются единичные векторы,
то проекции численно равны косинусам углов то проекции численно равны косинусам углов
между векторами нового и старого базиса. между векторами нового и старого базиса.
Например, коэффициенты в первом равенстве Например, коэффициенты в первом равенстве
выражения (выражения (1.81.8):):
(
)
x'xx'x
e,ecos
=
γ
(
)
y'xy'x
e,ecos
=
γ
(
)
z'xz'x
e,ecos
=
γ
