Презентация - Калинин А.В., Лушкин И.А. Гидравлика
Подождите немного. Документ загружается.


Интегральная
Интегральная
формула
формула
количества
количества
движения
движения
В
В
единицу
единицу
времени
времени
при
при
установившемся
установившемся
движении
движении
изменение
изменение
количества
количества
движения
движения
составит
составит
()
(
)
22
02 ср22 01 ср11 02 ср201ср1
ssQρα υ −αυ =ρ α υ −αυ
где
где
Q
Q
–
–
расход
расход
жидкости
жидкости
.
.
Импульс
Импульс
действующих
действующих
сил
сил
должен
должен
равняться
равняться
изменению
изменению
количества
количества
движения
движения
массы
массы
,
,
на
на
которую
которую
данный
данный
импульс
импульс
действует
действует
.
.
Следовательно
Следовательно
,
,
при
при
течении
течении
жидкости
жидкости
в
в
канале
канале
с
с
учетом
учетом
принятых
принятых
условий
условий
соблюдается
соблюдается
равенство
равенство
11 2 2
sin cos
SS
pds dspspsα+τ α+ −
∫∫
– gρVsin θ =
02 ср201ср1
QQ
ρ
αυ −ραυ
Нами
Нами
получено
получено
гидравлическое
гидравлическое
уравнение
уравнение
количества
количества
движения
движения
.
.
Вывод
Вывод
:
:
При
При
переходе
переходе
от
от
сечения
сечения
1
1
-
-
1
1
к
к
сечению
сечению
2
2
-
-
2
2
проекция
проекция
секундного
секундного
количества
количества
движения
движения
потока
потока
изменяется
изменяется
на
на
величину
величину
,
,
равную
равную
сумме
сумме
проекций
проекций
всех
всех
внешних
внешних
сил
сил
,
,
действующих
действующих
на
на
объем
объем
потока
потока
,
,
заключенный
заключенный
между
между
сечениями
сечениями
1
1
-
-
1
1
и
и
2
2
-
-
2.
2.
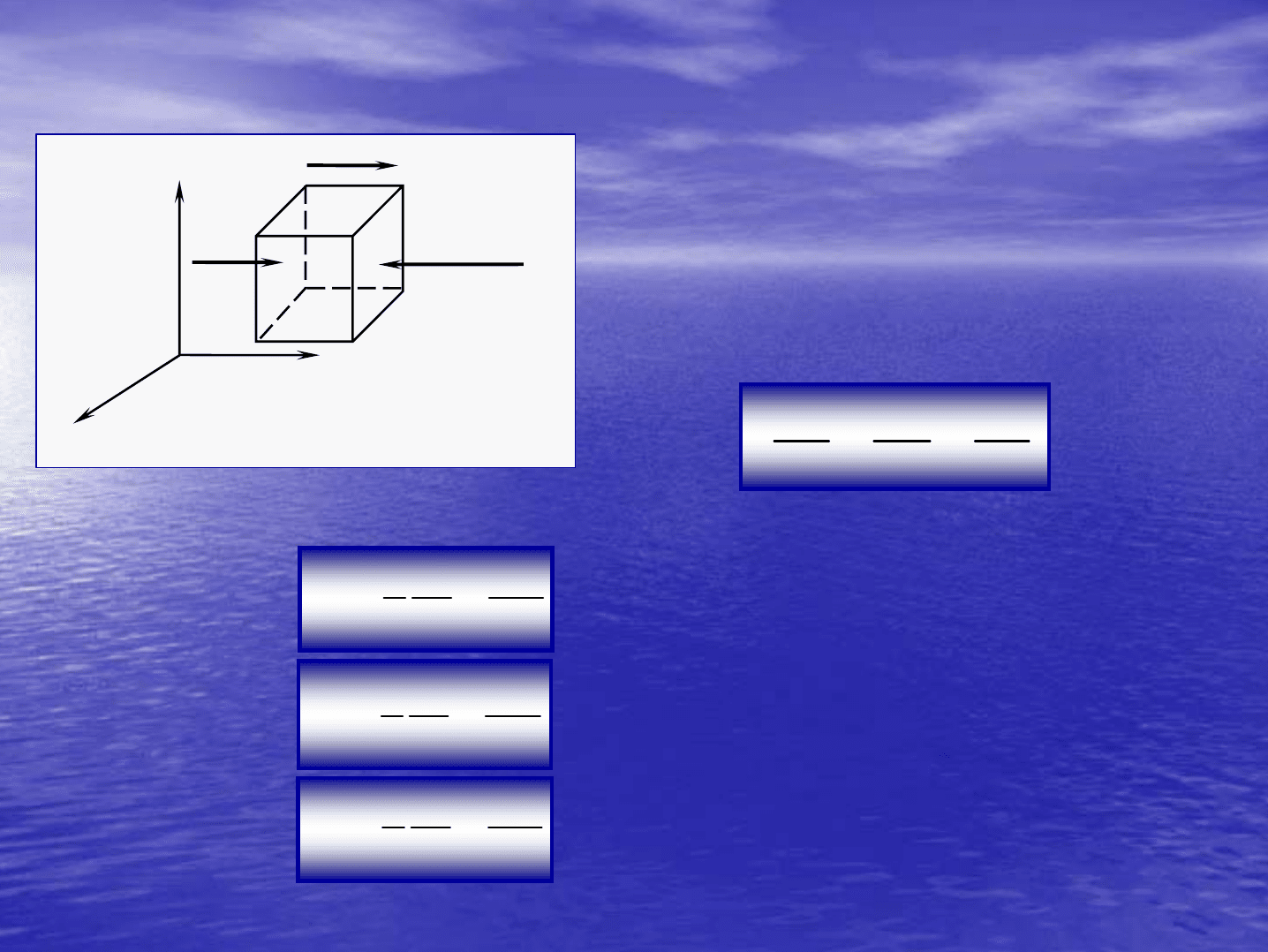
Дифференциальное
Дифференциальное
уравнение
уравнение
движения
движения
невязкой
невязкой
жидкости
жидкости
(
(
уравнение
уравнение
Эйлера
Эйлера
)
)
(
)
dydzpp
Δ
+
dx
dz
dy
y
z
x
pdydz
0
На
На
параллелепипед
параллелепипед
действуют
действуют
поверхностные
поверхностные
силы
силы
давления
давления
и
и
массовые
массовые
силы
силы
с
с
проекциями
проекциями
X, Y, Z,
X, Y, Z,
отнесенными
отнесенными
к
к
единице
единице
массы
массы
.
.
При
При
движении
движении
объема
объема
возникают
возникают
силы
силы
инерции
инерции
.
.
Проекции
Проекции
этих
этих
сил
сил
на
на
оси
оси
координат
координат
,
,
отнесенные
отнесенные
к
к
единице
единице
массы
массы
,
,
равны
равны
соответственно
соответственно
:
:
,,.
y
x
z
du
du
du
dt dt dt
−−−
Уравнения
Уравнения
равновесия
равновесия
будут
будут
выглядеть
выглядеть
следующим
следующим
образом
образом
1
x
du
p
xdt
∂
=
ρ∂
X ─
1
y
du
p
ydt
∂
=
ρ∂
Y ─
1
z
dup
zdt
∂
=
ρ∂
Z ─
Система
Система
уравнений
уравнений
Эйлера
Эйлера

Дифференциальное
Дифференциальное
уравнение
уравнение
движения
движения
невязкой
невязкой
жидкости
жидкости
(
(
уравнение
уравнение
Эйлера
Эйлера
)
)
Можно
Можно
получить
получить
полный
полный
дифференциал
дифференциал
уравнений
уравнений
Эйлера
Эйлера
для
для
установившегося
установившегося
движения
движения
,
,
если
если
рассматривать
рассматривать
перемещение
перемещение
частиц
частиц
жидкости
жидкости
вдоль
вдоль
линии
линии
тока
тока
.
.
Для
Для
этого
этого
надо
надо
умножить
умножить
каждое
каждое
из
из
уравнений
уравнений
системы
системы
на
на
соответствующую
соответствующую
проекцию
проекцию
элементарного
элементарного
перемещения
перемещения
частиц
частиц
dx
dx
,
,
dy
dy
,
,
dz
dz
,
,
и
и
сложить
сложить
их
их
:
:
(Xdx + Ydy + Zdz) –
1 ppp
dx dy dz
xyz
⎛⎞
∂∂∂
++
⎜⎟
ρ∂ ∂ ∂
⎝⎠
–
y
x
z
du
du du
dx dy dz
dt dt dt
⎛⎞
++
⎜⎟
⎝⎠
= 0.
Т.к. для установившегося течения линии тока совпадают с траекториями движения частиц, то
,,.
xyz
dx dy dz
uuu
dt dt dt
===
Тогда
y
x
z
du
du du
dx dy dz
dt dt dt
++ =
xx yx zz
udu udu udu++ =
222
1
()
2
xyz
du u u++ =
2
1
2
du
Для установившегося движения давление зависит только от координат, поэтому второй член
уравнения есть полный дифференциал давления dp. Получим
(Xdx + Ydy + Zdz) –
1
ρ
dp –
2
1
2
du = 0
Мы получили дифференциальное уравнение движения невязкой жидкости.

Дифференциальное
Дифференциальное
уравнение
уравнение
движения
движения
невязкой
невязкой
жидкости
жидкости
(
(
уравнение
уравнение
Эйлера
Эйлера
)
)
В поле силы тяжести
X = 0, Y = 0, Z = – g,
тогда уравнение запишется в следующем виде
– gdz –
dp
ρ
–
2
2
du
= 0.
После интегрирования этого уравнения получаем (при ρ = const) уравнение
gz +
p
ρ
+
2
2
u
= const,
которое называется уравнением Бернулли для струйки невязкой жидкости.

Общее
Общее
уравнение
уравнение
энергии
энергии
в
в
интегральной
интегральной
форме
форме
(
(
Уравнение
Уравнение
Бернулли
Бернулли
для
для
потока
потока
реальной
реальной
жидкости
жидкости
)
)
Для
Для
двух
двух
сечений
сечений
струйки
струйки
невязкой
невязкой
жидкости
жидкости
это
это
уравнение
уравнение
будет
будет
выглядеть
выглядеть
следующим
следующим
образом
образом
22
11 2 2
12
22
pu pu
gz gz
+
+= ++
ρρ
Сумма
Сумма
слева
слева
представляет
представляет
полную
полную
удельную
удельную
энергию
энергию
струйки
струйки
в
в
сечении
сечении
1
1
-
-
1,
1,
сумма
сумма
справа
справа
–
–
полную
полную
удельную
удельную
энергию
энергию
струйки
струйки
в
в
сечении
сечении
2
2
-
-
2.
2.
Можно
Можно
записать
записать
,
,
что
что
12
EE
=
В
В
процессе
процессе
движения
движения
вязкой
вязкой
жидкости
жидкости
запас
запас
ее
ее
механической
механической
энергии
энергии
уменьшается
уменьшается
,
,
и
и
на
на
самом
самом
деле
деле
12
E
Е>
Обозначим
Обозначим
энергию
энергию
,
,
затрачиваемую
затрачиваемую
на
на
преодоление
преодоление
сил
сил
сопротивления
сопротивления
E
E
пот
пот
.
.
Е
Е
1
1
=
=
Е
Е
2
2
+
+
E
E
пот
пот
.
.
Мощность
Мощность
потока
потока
складывается
складывается
из
из
энергии
энергии
отдельных
отдельных
струек
струек
S
NdN=
∫
где
где
N
N
–
–
мощность
мощность
потока
потока
;
;
dN
dN
–
–
мощность
мощность
струйки
струйки
.
.
dN = Ed
m
Q
= (gz +
p
ρ
+
2
2
u
) ρuds

Общее
Общее
уравнение
уравнение
энергии
энергии
в
в
интегральной
интегральной
форме
форме
(
(
Уравнение
Уравнение
Бернулли
Бернулли
для
для
потока
потока
реальной
реальной
жидкости
жидкости
)
)
Величина
Величина
удельной
удельной
энергии
энергии
потока
потока
равна
равна
частному
частному
от
от
деления
деления
мощности
мощности
потока
потока
на
на
массовый
массовый
расход
расход
2
2
S
m
pu
g
zuds
E
Q
⎛⎞
++ ρ
⎜⎟
ρ
⎝⎠
=
∫
Это
Это
уравнение
уравнение
можно
можно
разбить
разбить
на
на
два
два
интеграла
интеграла
E
=
пкин
E
Е
+
=
S
m
p
gz uds
Q
⎛⎞
+ρ
⎜⎟
ρ
⎝⎠
+
∫
2
2
S
m
u
uds
Q
⎛⎞
ρ
⎜⎟
⎝⎠
∫
где
где
–
–
удельная
удельная
потенциальная
потенциальная
энергия
энергия
потока
потока
относительно
относительно
выбранной
выбранной
плоскости
плоскости
сравнения
сравнения
;
;
–
–
удельная
удельная
кинетическая
кинетическая
энергия
энергия
потока
потока
.
.
п
E
кин
Е
п
E
=
S
m
p
g
zds
Q
⎛⎞
ρ+ υ
⎜⎟
ρ
⎝⎠
=
∫
m
p
g
zQ
Q
⎛⎞
+ρ
⎜⎟
ρ
⎝⎠
=
gz
p
+
ρ

Общее
Общее
уравнение
уравнение
энергии
энергии
в
в
интегральной
интегральной
форме
форме
(
(
Уравнение
Уравнение
Бернулли
Бернулли
для
для
потока
потока
реальной
реальной
жидкости
жидкости
)
)
Умножим
Умножим
и
и
поделим
поделим
это
это
выражение
выражение
на
на
3
ср
S
υ
2
2
S
m
u
uds
Q
⎛⎞
ρ
⎜⎟
⎝⎠
∫
3
ср
3
ср
S
S
υ
υ
=
2
ср
ср
2
S
υ
ρ
υ
3
3
ср
2
S
m
u
ds
SQυ
∫
=
2
ср
2
m
m
Q
Q
υ
α
где
где
α
α
–
–
коэффициент
коэффициент
,
,
который
который
учитывает
учитывает
неравномерность
неравномерность
распределения
распределения
скоростей
скоростей
в
в
сечении
сечении
,
,
называется
называется
коэффициент
коэффициент
Кориолиса
Кориолиса
.
.
кин
Е
=
2
ср
2
υ
α
Запишем
Запишем
уравнение
уравнение
Бернулли
Бернулли
для
для
двух
двух
сечений
сечений
потока
потока
реальной
реальной
жидкости
жидкости
22
11ср 22ср
12
12
22
пот
pp
gz gz E
αυ αυ
++ = ++ +
ρρ
Выводы
Выводы
:
:
1.
1.
При
При
увеличении
увеличении
кинетической
кинетической
энергии
энергии
потока
потока
от
от
одного
одного
сечения
сечения
к
к
другому
другому
потенциальная
потенциальная
энергия
энергия
уменьшается
уменьшается
,
,
и
и
,
,
наоборот
наоборот
,
,
с
с
увеличением
увеличением
потенциальной
потенциальной
энергии
энергии
,
,
кинетическая
кинетическая
уменьшается
уменьшается
.
.
2.
2.
Коэффициент
Коэффициент
α
α
тем
тем
больше
больше
,
,
чем
чем
больше
больше
скорости
скорости
отдельных
отдельных
струек
струек
отличаются
отличаются
от
от
величины
величины
средней
средней
скорости
скорости
.
.
Если
Если
скорости
скорости
всех
всех
элементарных
элементарных
струек
струек
будут
будут
равны
равны
средней
средней
скорости
скорости
,
,
то
то
α
α
=
=
1.
1.

Три
Три
формы
формы
представления
представления
уравнения
уравнения
Бернулли
Бернулли
для
для
потока
потока
реальной
реальной
жидкости
жидкости
Уравнение
Уравнение
Бернулли
Бернулли
в
в
форме
форме
напоров
напоров
можно
можно
получить
получить
,
,
если
если
разделить
разделить
уравнение
уравнение
в
в
форме
форме
удельной
удельной
энергии
энергии
на
на
g
g
,
,
обозначив
обозначив
пот
w
E
h
g
=
22
11ср 22ср
12
12
22
w
pp
zzh
gg gg
αυ αυ
+
+=+++
ρρ
0
H
h
′
′
h
′
d
1
d
2
d
1
z
′
γ
p
g2
2
υ
l
l
1
1
2
2
3
3
0

Три
Три
формы
формы
представления
представления
уравнения
уравнения
Бернулли
Бернулли
для
для
потока
потока
реальной
реальной
жидкости
жидкости
Уравнение
Уравнение
Бернулли
Бернулли
в
в
форме
форме
давлений
давлений
получаем
получаем
,
,
если
если
уравнение
уравнение
Бернулли
Бернулли
в
в
форме
форме
удельной
удельной
энергии
энергии
умножим
умножим
на
на
плотность
плотность
ρ
ρ
.
.
22
11ср 12ср
11 2 2
.
22
w
g
zp
g
zp
g
h
αυ αυ
ρ++ρ =ρ++ρ +ρ
Вывод
Вывод
:
:
при
при
увеличении
увеличении
скорости
скорости
движения
движения
потока
потока
давление
давление
на
на
этом
этом
участке
участке
падает
падает
и
и
,
,
наоборот
наоборот
–
–
при
при
уменьшении
уменьшении
скорости
скорости
давление
давление
увеличивается
увеличивается
.
.
Уравнение
Уравнение
Бернулли
Бернулли
в
в
форме
форме
давлений
давлений
применяется
применяется
для
для
расчета
расчета
систем
систем
вентиляции
вентиляции
,
,
газовых
газовых
стояков
стояков
внутри
внутри
зданий
зданий
и
и
т
т
.
.
д
д
.
.

Особенности
Особенности
турбулентного
турбулентного
и
и
ламинарного
ламинарного
течения
течения
жидкости
жидкости
.
.
Число
Число
Рейнольдса
Рейнольдса
Жидкость
Жидкость
в
в
круглой
круглой
трубе
трубе
движется
движется
как
как
бы
бы
концентрическими
концентрическими
кольцевыми
кольцевыми
слоями
слоями
,
,
которые
которые
не
не
перемешиваются
перемешиваются
между
между
собой
собой
.
.
Такое
Такое
движение
движение
называется
называется
ламинарным
ламинарным
(
(
слоистым
слоистым
)
)
Отдельные
Отдельные
частицы
частицы
жидкости
жидкости
и
и
ее
ее
небольшие
небольшие
объемы
объемы
пребывают
пребывают
в
в
состоянии
состоянии
хаотического
хаотического
и
и
беспорядочного
беспорядочного
движения
движения
.
.
Наряду
Наряду
с
с
общими
общими
поступательными
поступательными
движениями
движениями
имеется
имеется
поперечное
поперечное
перемещение
перемещение
частиц
частиц
.
.
Такое
Такое
движение
движение
называется
называется
турбулентным
турбулентным
Характеристика Ламинарный режим Турбулентный режим
Движение Только продольное Продольное и поперечное
Потери энергии
1
w
g
hu
≡
2
w
g
hu
≡
Передача тепла
Теплообмен за счет
теплопроводности
Теплообмен за счет
теплопроводности и конвекции
Эпюра скорости Параболическая функция Логарифмическая функция
Коэффициент α α = 2
1
α
≈
