Презентация - Калинин А.В., Лушкин И.А. Гидравлика
Подождите немного. Документ загружается.

Измерительные
Измерительные
приборы
приборы
,
,
используемые
используемые
при
при
проведении
проведении
экспериментальных
экспериментальных
работ
работ
3.
3.
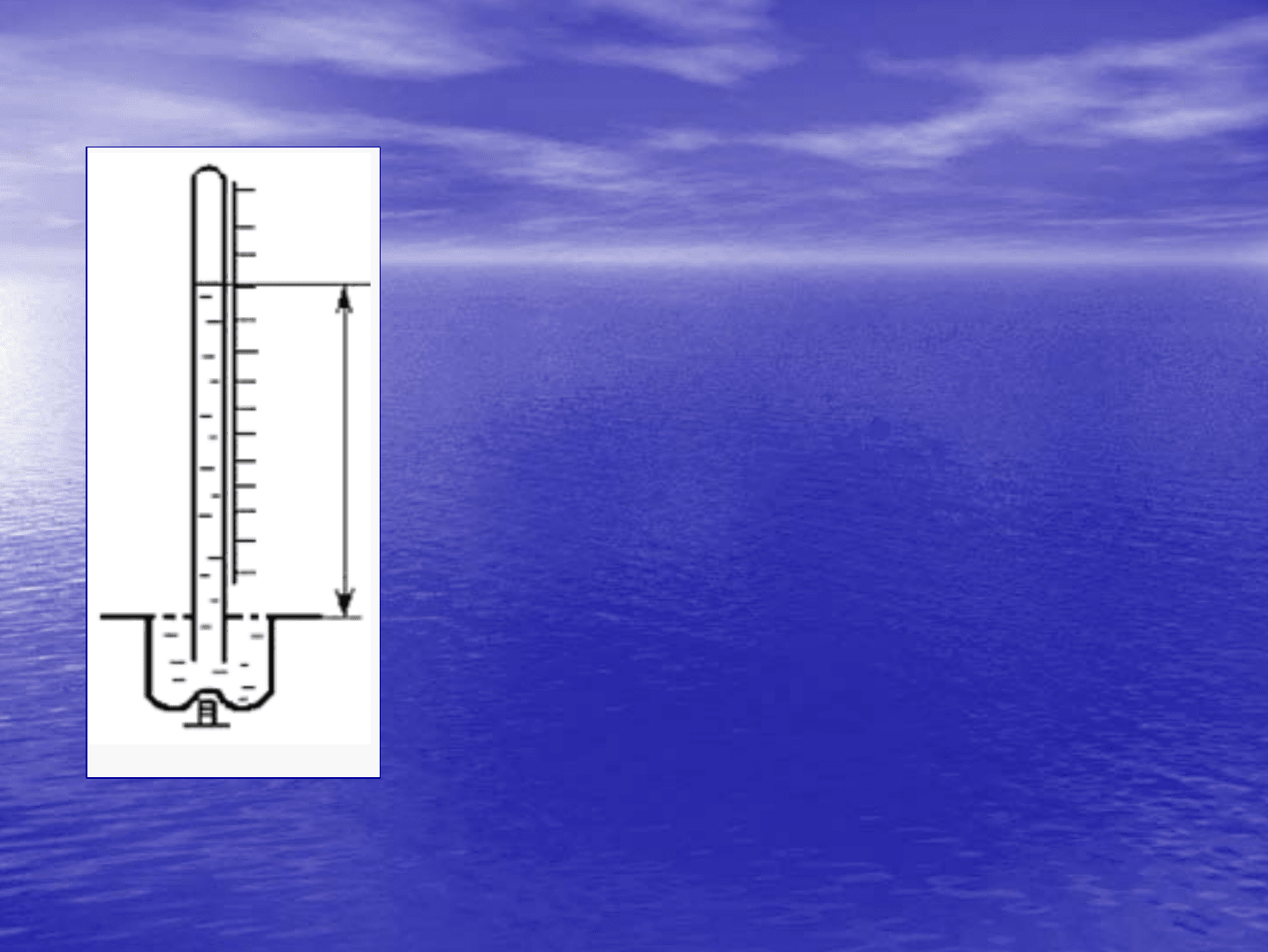
Барометры
Барометры
.
.
H
R
V
Барометры
Барометры
используются
используются
для
для
измерения
измерения
атмосферного
атмосферного
давления
давления
.
.
В
В
лабораторных
лабораторных
условиях
условиях
используется
используется
барометр
барометр
Фортина
Фортина
,
,
позволяющий
позволяющий
довольно
довольно
точно
точно
измерить
измерить
атмосферное
атмосферное
давление
давление
.
.
4.
4.
Вакуумметры
Вакуумметры
.
.
Принцип
Принцип
действия
действия
механического
механического
и
и
жидкостного
жидкостного
вакуумметров
вакуумметров
аналогичен
аналогичен
принципу
принципу
действия
действия
механического
механического
манометра
манометра
и
и
жидкостного
жидкостного
пьезометра
пьезометра
.
.
Измерительные
Измерительные
приборы
приборы
,
,
используемые
используемые
при
при
проведении
проведении
экспериментальных
экспериментальных
работ
работ
5.
5.
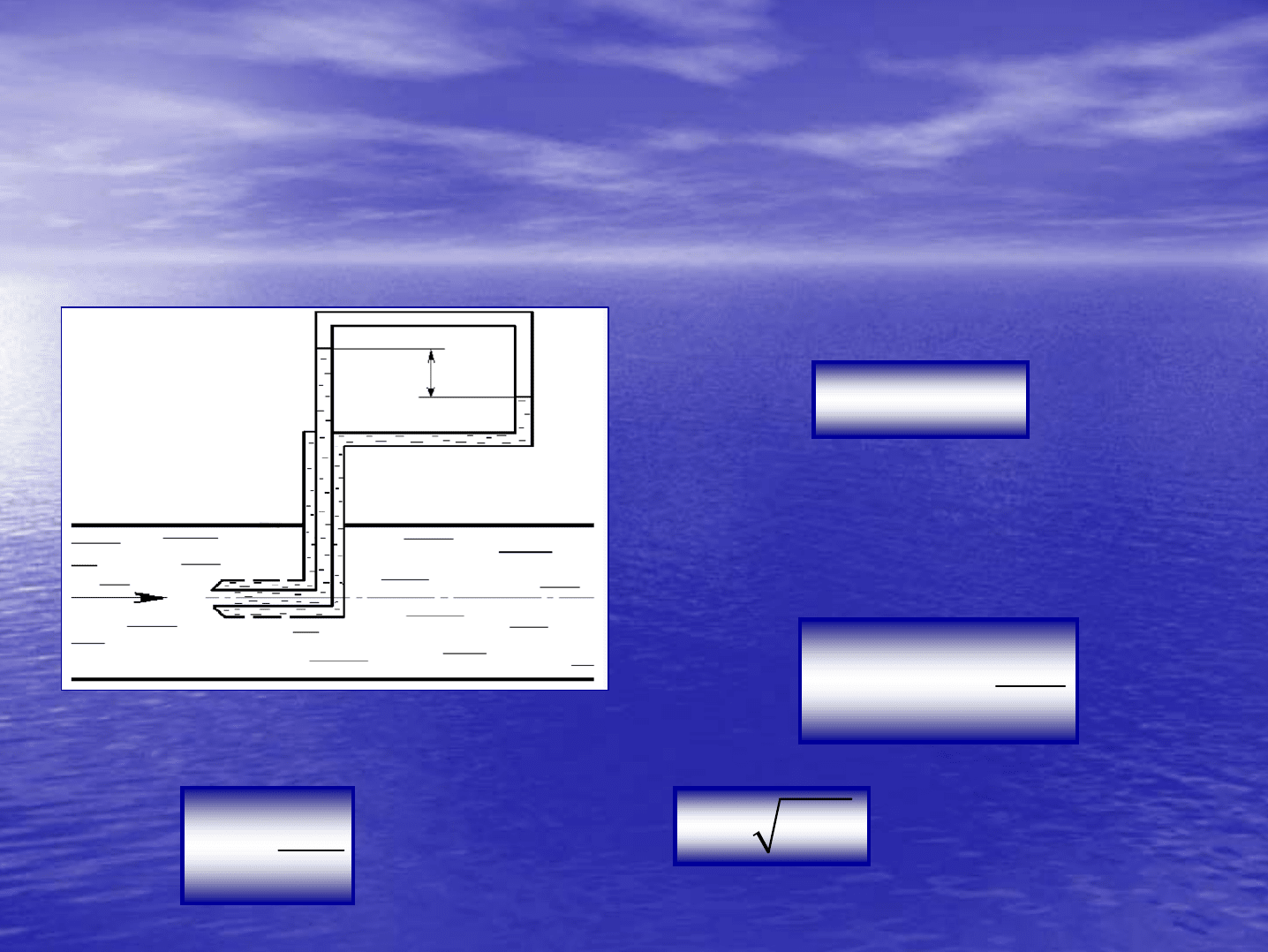
Трубка
Трубка
Пито
Пито
–
–
Прандтля
Прандтля
.
.
Трубка
Трубка
Пито
Пито
–
–
Прандтля
Прандтля
позволяет
позволяет
одновременно
одновременно
определить
определить
величину
величину
динамического
динамического
и
и
статического
статического
давления
давления
в
в
определенной
определенной
точке
точке
потока
потока
.
.
A
′
M
′
Δ
h
M
M
A
Разность
Разность
давления
давления
в
в
точках
точках
А
А
′
′
и
и
М
М
′
′
будет
будет
p
gh
Δ
=ρ
Разность
Разность
давления
давления
Δ
Δ
p
p
зависит
зависит
от
от
динамического
динамического
давления
давления
на
на
входе
входе
в
в
трубку
трубку
Пито
Пито
–
–
Прандтля
Прандтля
,
,
что
что
следует
следует
из
из
уравнения
уравнения
Бернулли
Бернулли
для
для
точек
точек
А
А
и
и
М
М
:
:
2
2
MA
pp
ρ
υ
=+
где
где
υ
υ
–
–
скорость
скорость
потока
потока
на
на
входе
входе
в
в
трубку
трубку
Пито
Пито
–
–
Прандтля
Прандтля
.
.
Таким
Таким
образом
образом
,
,
2
2
p
ρυ
Δ=
откуда
откуда
получаем
получаем
2.ghυ=
Измерительные
Измерительные
приборы
приборы
,
,
используемые
используемые
при
при
проведении
проведении
экспериментальных
экспериментальных
работ
работ
6.
6.
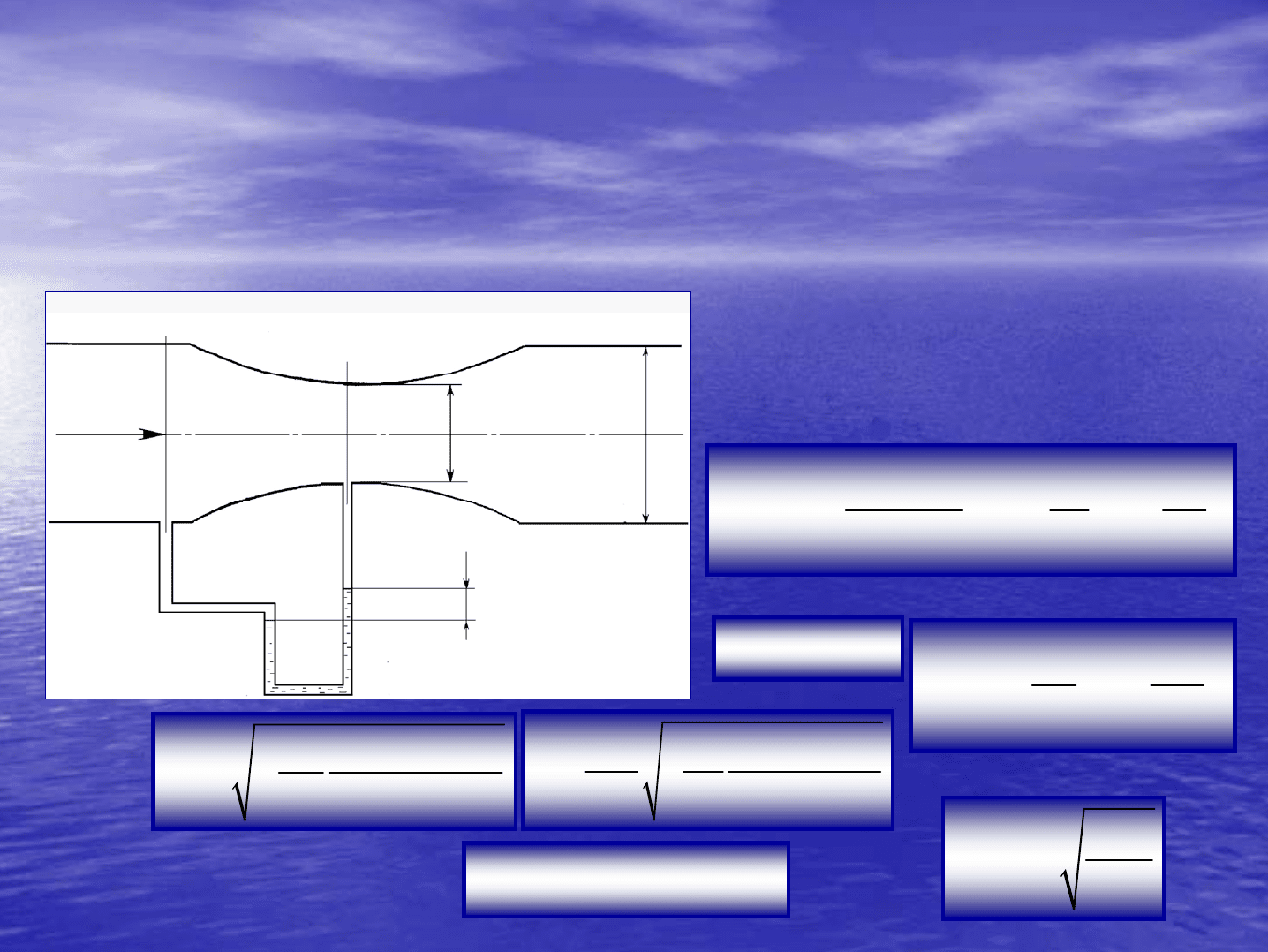
Расходомер
Расходомер
Вентури
Вентури
.
.
Расходомер
Расходомер
служит
служит
для
для
измерения
измерения
расхода
расхода
жидкости
жидкости
и
и
представляет
представляет
собой
собой
плавную
плавную
сходящуюся
сходящуюся
–
–
расходящуюся
расходящуюся
вставку
вставку
,
,
к
к
которой
которой
подключается
подключается
дифферциальный
дифферциальный
манометр
манометр
.
.
1
1
2
2
d
D
h
Для
Для
вывода
вывода
расчетной
расчетной
формулы
формулы
применим
применим
уравнение
уравнение
Бернулли
Бернулли
для
для
сечения
сечения
1
1
-
-
1
1
перед
перед
сужением
сужением
и
и
сечения
сечения
2
2
-
-
2
2
в
в
сужении
сужении
(
(
α
α
1
1
=
=
α
α
2
2
= 1).
= 1).
22 2 2
21 2 1
2
2
1
22
v
p
⎛⎞
⎛⎞
υ
−υ υ
Δ=ρ =ρ −
⎜⎟
⎜⎟
υ
⎝⎠
⎝⎠
С
С
учетом
учетом
уравнения
уравнения
неразрывности
неразрывности
11 2 2
SSυ=υ
24
2
4
1
2
d
p
D
⎛⎞
υ
Δ=ρ −
⎜⎟
⎝⎠
Откуда
Откуда
2
44
1
2
1( / )
p
dD
Δ
υ=
ρ−
2
44
1
2
41(/)
dp
Q
dD
πΔ
=
ρ−
Для
Для
ртутного
ртутного
манометра
манометра
рт ж
()pgh
Δ
=ρ −ρ
2 p
QS
Δ
=μ
ρ
Измерительные
Измерительные
приборы
приборы
,
,
используемые
используемые
при
при
проведении
проведении
экспериментальных
экспериментальных
работ
работ
7.
7.
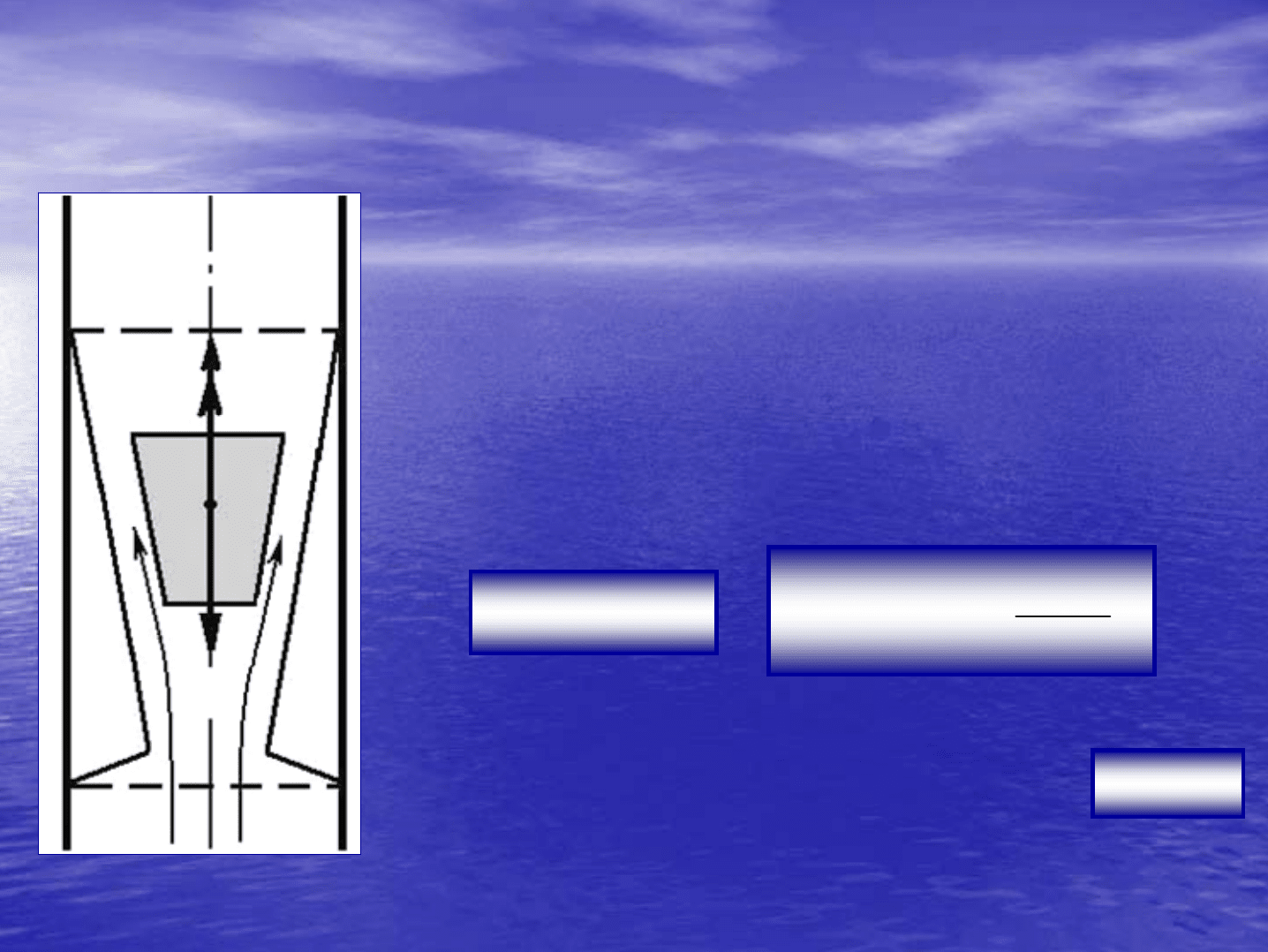
Ротаметры
Ротаметры
.
.
F
F
A
G
Ротаметры
Ротаметры
используются
используются
для
для
измерения
измерения
расхода
расхода
жидкостей
жидкостей
,
,
имеющих
имеющих
слабые
слабые
коррозийные
коррозийные
свойства
свойства
.
.
Ротаметр
Ротаметр
состоит
состоит
из
из
сужающейся
сужающейся
стеклянной
стеклянной
трубки
трубки
и
и
металлического
металлического
конусообразного
конусообразного
измерителя
измерителя
.
.
На
На
измеритель
измеритель
действуют
действуют
следующие
следующие
силы
силы
:
:
сила
сила
тяжести
тяжести
G
G
,
,
архимедова
архимедова
сила
сила
F
F
A
A
,
,
сила
сила
динамического
динамического
давления
давления
жидкости
жидкости
F
F
.
.
Для
Для
измерителя
измерителя
,
,
находящегося
находящегося
в
в
покое
покое
,
,
можно
можно
записать
записать
A
GFF
=
+
2
ж
ж
2
mg Vg S
ρ
υ
=ρ +
Сила
Сила
тяжести
тяжести
и
и
архимедова
архимедова
сила
сила
–
–
величины
величины
постоянные
постоянные
,
,
поэтому
поэтому
сила
сила
динамического
динамического
давления
давления
жидкости
жидкости
при
при
любом
любом
расходе
расходе
QS
=
υ
будет
будет
также
также
постоянной
постоянной
.
.

Гидравлические
Гидравлические
сопротивления
сопротивления
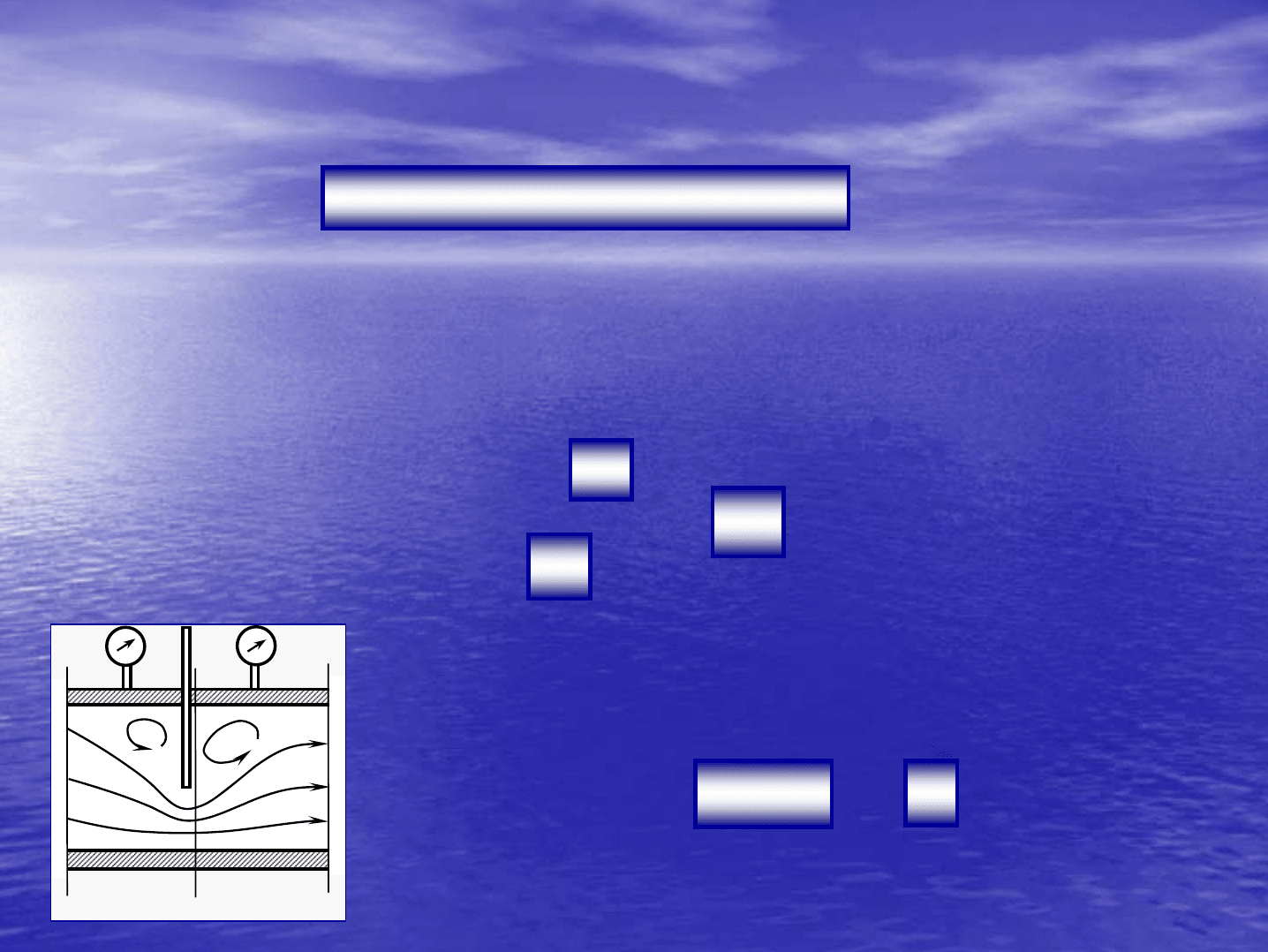
Виды
Виды
гидравлических
гидравлических
сопротивлений
сопротивлений
Потери
Потери
по
по
длине
длине
Уравнение
Уравнение
Бернулли
Бернулли
можно
можно
записать
записать
в
в
следующем
следующем
виде
виде
12 длw пот w
pp gh E p р
−
=ρ =ρ = =
Вывод
Вывод
:
:
Работа
Работа
сил
сил
давления
давления
расходуется
расходуется
на
на
преодоление
преодоление
сил
сил
трения
трения
,
,
что
что
и
и
обуславливает
обуславливает
потери
потери
механической
механической
энергии
энергии
,
,
которые
которые
прямо
прямо
пропорциональны
пропорциональны
длине
длине
пути
пути
движения
движения
.
.
В
В
зависимости
зависимости
от
от
формы
формы
записи
записи
уравнения
уравнения
Бернулли
Бернулли
эти
эти
потери
потери
называются
называются
:
:
•
•
потерями
потерями
давления
давления
по
по
длине
длине
•
•
потерями
потерями
удельной
удельной
энергии
энергии
по
по
длине
длине
•
•
потерями
потерями
напора
напора
по
по
длине
длине
дл
p
дл
Е
дл
h
Местные
Местные
потери
потери
Образуются
Образуются
в
в
результате
результате
изменения
изменения
структуры
структуры
потока
потока
по
по
пути
пути
движения
движения
жидкости
жидкости
C
C
1
1
2
2
В
В
зависимости
зависимости
от
от
формы
формы
записи
записи
местные
местные
потери
потери
записываются
записываются
как
как
мм
,,
р
Е
м
h
или
или
Общие
Общие
потери
потери
в
в
трубопроводе
трубопроводе
складываются
складываются
из
из
потерь
потерь
по
по
длине
длине
и
и
потерь
потерь
на
на
местных
местных
сопротивлениях
сопротивлениях
Сопротивление
Сопротивление
по
по
длине
длине
при
при
движении
движении
в
в
цилиндрической
цилиндрической
трубе
трубе
при
при
ламинарном
ламинарном
течении
течении
При
При
ламинарном
ламинарном
режиме
режиме
жидкость
жидкость
движется
движется
концентрическими
концентрическими
слоями
слоями
.
.
Воспользуемся
Воспользуемся
формулой
формулой
Ньютона
Ньютона
для
для
напряжений
напряжений
трения
трения
,
,
приняв
приняв
du
dr
τ=−μ
d
y
dr=
Знак
Знак
«
«
минус
минус
»
»
указывает
указывает
на
на
то
то
,
,
что
что
скорость
скорость
уменьшается
уменьшается
в
в
направлении
направлении
оси
оси
r
r
(
(
от
от
центра
центра
к
к
стенке
стенке
трубы
трубы
).
).
l
T
T
P
2
P
1
2r
0
r
h
дл
1
1
2
2
На
На
выделенный
выделенный
объем
объем
действуют
действуют
внешние
внешние
силы
силы
:
:
нормальные
нормальные
к
к
живым
живым
сечениям
сечениям
:
:
силы
силы
давления
давления
,
,
и
и
касательные
касательные
силы
силы
сопротивления
сопротивления
Т
Т
,
,
приложенные
приложенные
к
к
боковой
боковой
поверхности
поверхности
11
P
pS
=
22
P
pS
=
2TS rl
=
τ= π τ

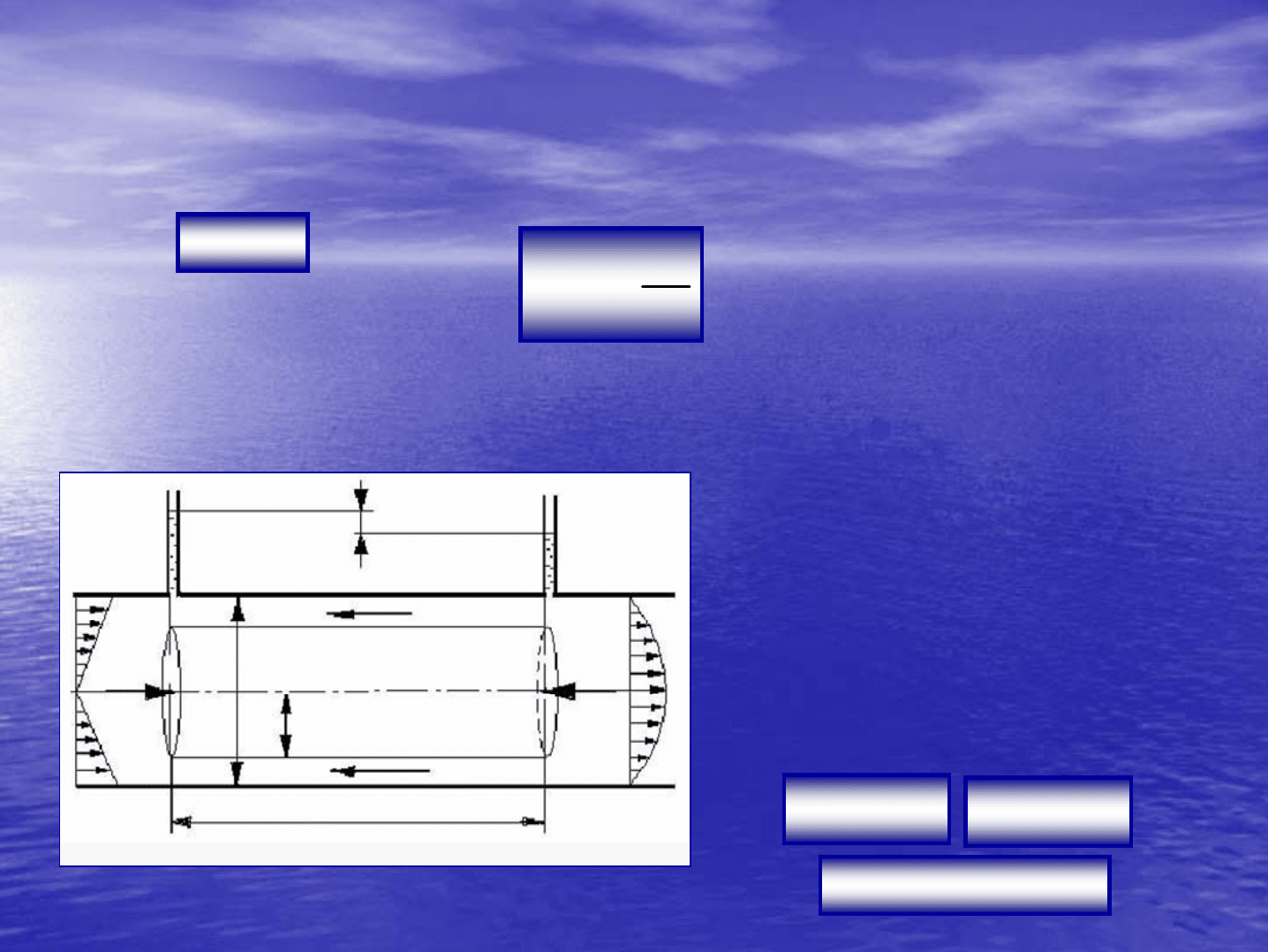
Сопротивление
Сопротивление
по
по
длине
длине
при
при
движении
движении
в
в
цилиндрической
цилиндрической
трубе
трубе
при
при
ламинарном
ламинарном
течении
течении
12
()
2
p
pr
l
−
τ=
Вывод
Вывод
:
:
При
При
ламинарном
ламинарном
движении
движении
в
в
круглой
круглой
трубе
трубе
напряжение
напряжение
трения
трения
максимально
максимально
у
у
стенки
стенки
и
и
равно
равно
0
0
на
на
оси
оси
трубы
трубы
Закон
Закон
распределения
распределения
скоростей
скоростей
Граничные
Граничные
условия
условия
:
:
0
rr
=
0u
=
2
120
()
4
ppr
const
l
−
=
μ
22
120
()()
4
p
pr r
u
l
−−
=
μ
Вывод
Вывод
:
:
При
При
ламинарном
ламинарном
течении
течении
скорости
скорости
в
в
сечении
сечении
трубки
трубки
распределяются
распределяются
по
по
параболическому
параболическому
закону
закону
Уравнение
Уравнение
равновесия
равновесия
этих
этих
сил
сил
относительно
относительно
направления
направления
движения
движения
:
:
12
P
PT
=
+
22
12
2pr pr rl
π
=π+πτ
12
2
pp
lr
−
τ
=
Закон
Закон
распределения
распределения
скоростей
скоростей
по
по
сечению
сечению
трубы
трубы
можно
можно
получить
получить
из
из
следующего
следующего
уравнения
уравнения
12
()pprdr
2
du
l
−
=
μ
После
После
интегрирования
интегрирования
,
,
получаем
получаем
:
:
2
12
()
4
ppr
u const
l
−
=− +
μ

Сопротивление
Сопротивление
по
по
длине
длине
при
при
движении
движении
в
в
цилиндрической
цилиндрической
трубе
трубе
при
при
ламинарном
ламинарном
течении
течении
Максимальная
Максимальная
скорость
скорость
на
на
оси
оси
трубы
трубы
будет
будет
при
при
r
r
= 0
= 0
2
max
2
0
1
r
uu
r
⎛⎞
=−
⎜⎟
⎝⎠
Полный
Полный
расход
расход
2
0
max
2
r
Qu
π
=
Вывод
Вывод
:
:
Для
Для
того
того
чтобы
чтобы
определить
определить
расход
расход
при
при
ламинарном
ламинарном
режиме
режиме
достаточно
достаточно
измерить
измерить
скорость
скорость
на
на
оси
оси
потока
потока
и
и
умножить
умножить
ее
ее
на
на
половину
половину
площади
площади
живого
живого
сечения
сечения
.
.
Средняя
Средняя
скорость
скорость
max
ср
2
u
υ=
Вывод
Вывод
:
:
Средняя
Средняя
скорость
скорость
при
при
ламинарном
ламинарном
режиме
режиме
в
в
два
два
раза
раза
меньше
меньше
скорости
скорости
на
на
оси
оси
потока
потока
.
.
Закон
Закон
сопротивления
сопротивления
при
при
ламинарном
ламинарном
режиме
режиме
дл
4
0
8 lQ
h
r
g
ν
=
π
Вывод
Вывод
:
:
Потери
Потери
напора
напора
на
на
преодоление
преодоление
сил
сил
сопротивления
сопротивления
по
по
длине
длине
при
при
ламинарном
ламинарном
режиме
режиме
прямопропорциональны
прямопропорциональны
расходу
расходу
и
и
длине
длине
трубопровода
трубопровода
и
и
обратнопропорциональны
обратнопропорциональны
радиусу
радиусу
трубы
трубы
в
в
четверной
четверной
степени
степени
.
.

Формула
Формула
Дарси
Дарси
-
-
Вейсбаха
Вейсбаха
2
ср
дл
2
l
h
dg
υ
=λ
Формула
Формула
Дарси
Дарси
-
-
Вейсбаха
Вейсбаха
для
для
определения
определения
потерь
потерь
напора
напора
по
по
длине
длине
64
Re
λ=
–
–
коэффициент
коэффициент
гидравлического
гидравлического
трения
трения
Заменим
Заменим
в
в
формуле
формуле
дл
4
0
8 lQ
h
rg
ν
=
π
2
ср
4
d
Q
π
=υ
4
4
0
16
d
r =
Получаем
Получаем
формулу
формулу
Пуазейля
Пуазейля
ср
дл
2
32 l
h
g
d
νυ
=
Перепишем
Перепишем
формулу
формулу
Пуазейля
Пуазейля
следующим
следующим
образом
образом
ср
дл
32
l
h
dd g
υ
ν
=
умножим
умножим
и
и
разделим
разделим
на
на
ср
2
υ
ср
ср
дл
ср
2
32
2
l
h
dd g
υ
υ
ν
=
υ
2
ср
дл
ср
64
2
l
h
dd g
υ
ν
=
υ
Если
Если
ср
1
Red
ν
=
υ
то
то
получаем
получаем
2
ср
дл
64
Re 2
l
h
dg
υ
=
