Презентация - Калинин А.В., Лушкин И.А. Гидравлика
Подождите немного. Документ загружается.

Особенности
Особенности
турбулентного
турбулентного
и
и
ламинарного
ламинарного
течения
течения
жидкости
жидкости
.
.
Число
Число
Рейнольдса
Рейнольдса
Режим
Режим
зависит
зависит
от
от
трех
трех
параметров
параметров
:
:
средней
средней
скорости
скорости
,
,
диаметра
диаметра
и
и
кинематической
кинематической
вязкости
вязкости
ν
ν
.
.
Рейнальдс
Рейнальдс
пришел
пришел
к
к
выводу
выводу
,
,
что
что
существует
существует
некоторое
некоторое
критическое
критическое
значение
значение
соотношения
соотношения
этих
этих
параметров
параметров
,
,
являющееся
являющееся
границей
границей
между
между
ламинарными
ламинарными
и
и
турбулентными
турбулентными
режимами
режимами
течения
течения
,
,
и
и
нашел
нашел
его
его
:
:
ср
Re 2320.
d
υ
⋅
==
ν
Хаотичность
Хаотичность
турбулентного
турбулентного
движения
движения
с
с
кинематической
кинематической
точки
точки
зрения
зрения
означает
означает
,
,
что
что
скорость
скорость
движения
движения
в
в
отдельных
отдельных
точках
точках
пространства
пространства
непрерывно
непрерывно
изменяется
изменяется
как
как
по
по
величине
величине
,
,
так
так
и
и
по
по
направлению
направлению
.
.
Скорость
Скорость
в
в
данной
данной
точке
точке
турбулентного
турбулентного
потока
потока
,
,
измеренную
измеренную
в
в
данный
данный
момент
момент
времени
времени
,
,
называют
называют
мгновенной
мгновенной
и
и
обозначают
обозначают
u
u
.
.
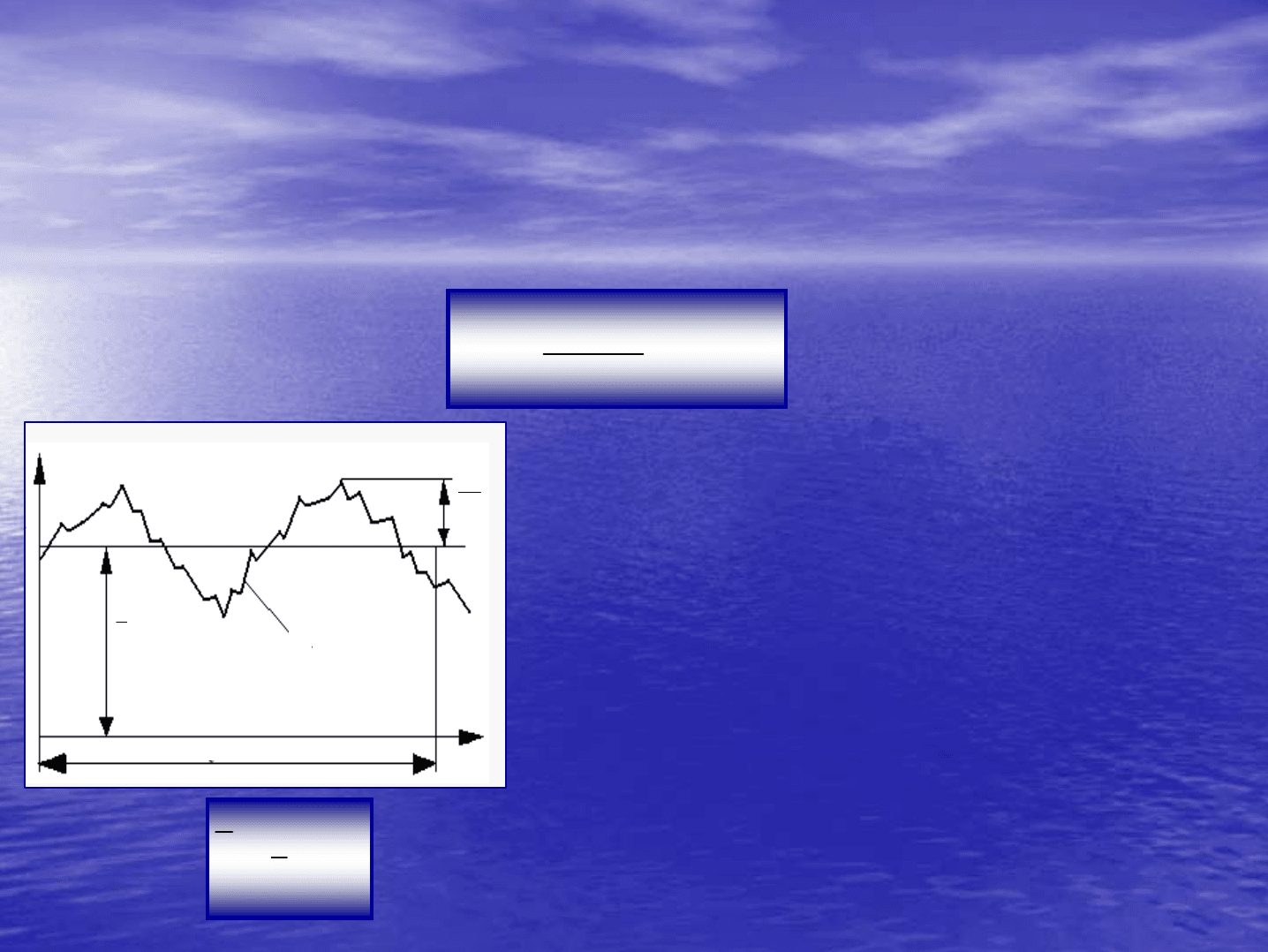
Экспериментальные
Экспериментальные
исследования
исследования
показывают
показывают
,
,
что
что
изменения
изменения
мгновенной
мгновенной
скорости
скорости
носит
носит
случайный
случайный
характер
характер
.
.
u
t
u
u
uΔ
t
0
1
t
uudt
t
=
∫
где
где
t
t
–
–
достаточно
достаточно
длинный
длинный
интервал
интервал
времени
времени
.
.

Особенности
Особенности
турбулентного
турбулентного
и
и
ламинарного
ламинарного
течения
течения
жидкости
жидкости
.
.
Число
Число
Рейнольдса
Рейнольдса
Отклонение
Отклонение
мгновенной
мгновенной
скорости
скорости
от
от
ее
ее
осредненного
осредненного
значения
значения
называют
называют
пульсационной
пульсационной
скоростью
скоростью
или
или
пульсацией
пульсацией
.
.
Замена
Замена
действительных
действительных
беспорядочных
беспорядочных
движений
движений
жидких
жидких
комков
комков
на
на
фиктивное
фиктивное
струйное
струйное
движение
движение
требует
требует
введения
введения
некоторых
некоторых
фиктивных
фиктивных
сил
сил
взаимодействия
взаимодействия
между
между
воображаемыми
воображаемыми
струйками
струйками
.
.
Благодаря
Благодаря
этому
этому
Прандтлем
Прандтлем
был
был
введен
введен
новый
новый
вид
вид
поверхностных
поверхностных
сил
сил
и
и
соответствующих
соответствующих
касательных
касательных
напряжений
напряжений
uuu
Δ
=−
x
yxy
uu
τ
=−ρΔ Δ
которые
которые
называются
называются
турбулентными
турбулентными
касательными
касательными
напряжениями
напряжениями
.
.
Осредненные
Осредненные
касательные
касательные
напряжения
напряжения
называются
называются
турбулентными
турбулентными
турб
x
y
uu
τ
=−ρΔ Δ
Полное
Полное
касательное
касательное
напряжение
напряжение
турбулентного
турбулентного
потока
потока
турб вязк
x
xy
du
uu
dy
τ=τ +τ =−ρΔ Δ +μ

Уравнение
Уравнение
Бернулли
Бернулли
для
для
элементарной
элементарной
струйки
струйки
невязкой
невязкой
сжимаемой
сжимаемой
жидкости
жидкости
Плотность
Плотность
сжимаемой
сжимаемой
жидкости
жидкости
изменяется
изменяется
в
в
процессе
процессе
движения
движения
2
2
dp u
g
zconst++=
ρ
∫
При
При
установившемся
установившемся
движении
движении
влияние
влияние
сжимаемости
сжимаемости
практически
практически
проявляется
проявляется
только
только
в
в
газах
газах
,
,
при
при
анализе
анализе
течения
течения
которых
которых
удельной
удельной
энергией
энергией
положения
положения
можно
можно
пренебречь
пренебречь
.
.
2
2
dp u
const+=
ρ
∫
Это
Это
уравнение
уравнение
можно
можно
назвать
назвать
уравнением
уравнением
Бернулли
Бернулли
для
для
сжимаемой
сжимаемой
жидкости
жидкости
.
.
Вывод
Вывод
:
:
При
При
установившемся
установившемся
течении
течении
невязкого
невязкого
газа
газа
сумма
сумма
удельной
удельной
потенциальной
потенциальной
,
,
внутренней
внутренней
и
и
кинетической
кинетической
энергии
энергии
есть
есть
величина
величина
постоянная
постоянная
.
.
Изменение
Изменение
скорости
скорости
вдоль
вдоль
трубки
трубки
тока
тока
сжимаемого
сжимаемого
газа
газа
связано
связано
с
с
изменением
изменением
температуры
температуры
.
.
При
При
увеличении
увеличении
скорости
скорости
температура
температура
падает
падает
и
и
наоборот
наоборот
.
.
Для
Для
вычисления
вычисления
интеграла
интеграла
необходимо
необходимо
знать
знать
процесс
процесс
изменения
изменения
состояния
состояния
газа
газа
при
при
этом
этом
течении
течении
.
.
Такой
Такой
процесс
процесс
описывается
описывается
уравнением
уравнением
k
p
C
=
ρ
где
где
k
k
–
–
показатель
показатель
адиабаты
адиабаты
процесса
процесса
;
;
С
С
–
–
постоянная
постоянная
.
.
Теперь
Теперь
уравнение
уравнение
Бернулли
Бернулли
для
для
сжимаемой
сжимаемой
жидкости
жидкости
принимает
принимает
вид
вид
2
12
kpu
const
k
⋅+ =
−ρ
Поскольку
Поскольку
отношение
отношение
p
RT=
ρ
2
12
ku
R
Tconst
k
⋅+=
−

Уравнение
Уравнение
Бернулли
Бернулли
для
для
потока
потока
вязкой
вязкой
сжимаемой
сжимаемой
жидкости
жидкости
Заменив
Заменив
в
в
уравнении
уравнении
для
для
струйки
струйки
скорость
скорость
струйки
струйки
u
u
на
на
среднюю
среднюю
скорость
скорость
потока
потока
υ
υ
ср
ср
,
,
можно
можно
сразу
сразу
написать
написать
уравнение
уравнение
Бернулли
Бернулли
сжимаемой
сжимаемой
невязкой
невязкой
жидкости
жидкости
2
ср
12
k
RT const
k
υ
⋅+ =
−
Уравнение
Уравнение
Бернулли
Бернулли
для
для
вязкой
вязкой
сжимаемой
сжимаемой
жидкости
жидкости
0,
п
dp
ddE
+
νν+ =
ρ
Дифференциальное
Дифференциальное
уравнение
уравнение
движения
движения
При
При
адиабатическом
адиабатическом
течении
течении
,
,
где
где
отсутствует
отсутствует
обмен
обмен
тепла
тепла
со
со
средой
средой
вне
вне
границ
границ
потока
потока
,
,
можно
можно
получить
получить
уравнение
уравнение
движения
движения
в
в
конечном
конечном
виде
виде
,
dp
di dq=+
ρ
где
где
q
q
–
–
количество
количество
тепла
тепла
,
,
передаваемое
передаваемое
1
1
кг
кг
газа
газа
.
.
2
2
dp u
g
zconst++=
ρ
∫
Вывод
Вывод
:
:
При
При
установившемся
установившемся
течении
течении
невязкого
невязкого
газа
газа
сумма
сумма
удельной
удельной
потенциальной
потенциальной
,
,
внутренней
внутренней
и
и
кинетической
кинетической
энергии
энергии
есть
есть
величина
величина
постоянная
постоянная
.
.

Основы
Основы
моделирования
моделирования
гидромеханических
гидромеханических
процессов
процессов

Основы
Основы
моделирования
моделирования
При
При
изучении
изучении
гидроаэродинамических
гидроаэродинамических
явлений
явлений
необходимо
необходимо
широкое
широкое
применение
применение
эксперимента
эксперимента
.
.
Например
Например
,
,
все
все
вопросы
вопросы
,
,
касающиеся
касающиеся
турбулентного
турбулентного
движения
движения
жидкости
жидкости
,
,
не
не
имеют
имеют
точного
точного
теоретического
теоретического
решения
решения
,
,
поэтому
поэтому
экспериментальные
экспериментальные
решения
решения
дополняют
дополняют
теоретические
теоретические
.
.
Все
Все
виды
виды
гидравлических
гидравлических
сопротивлений
сопротивлений
и
и
соответствующие
соответствующие
им
им
коэффициенты
коэффициенты
определяются
определяются
экспериментальным
экспериментальным
путем
путем
.
.
Различают
Различают
математическое
математическое
моделирование
моделирование
(
(
на
на
ЭВМ
ЭВМ
)
)
и
и
физическое
физическое
(
(
на
на
физических
физических
моделях
моделях
).
).
Обоснование
Обоснование
моделирования
моделирования
и
и
использование
использование
в
в
натуре
натуре
результатов
результатов
экспериментов
экспериментов
на
на
модели
модели
связано
связано
с
с
подобием
подобием
движения
движения
в
в
натуре
натуре
и
и
на
на
модели
модели
.
.
Подобными
Подобными
называют
называют
явления
явления
,
,
происходящие
происходящие
в
в
геометрически
геометрически
подобных
подобных
системах
системах
одинаковой
одинаковой
физической
физической
природы
природы
,
,
когда
когда
одинаковые
одинаковые
величины
величины
(
(
например
например
скорости
скорости
или
или
силы
силы
),
),
действующие
действующие
в
в
подобных
подобных
точках
точках
,
,
имеют
имеют
между
между
собой
собой
постоянные
постоянные
отношения
отношения
,
,
которые
которые
называются
называются
масштабами
масштабами
.
.

Виды
Виды
подобия
подобия
.
.
Масштабы
Масштабы
моделирования
моделирования
Для
Для
установления
установления
подобия
подобия
гидроаэродинамических
гидроаэродинамических
явлений
явлений
между
между
натурой
натурой
и
и
моделью
моделью
следует
следует
использовать
использовать
правила
правила
механического
механического
подобия
подобия
.
.
Механическое
Механическое
подобие
подобие
подразумевает
подразумевает
выполнение
выполнение
геометрического
геометрического
,
,
кинематического
кинематического
и
и
динамического
динамического
подобия
подобия
.
.
Геометрически
Геометрически
подобными
подобными
являются
являются
два
два
потока
потока
н
l
м
l
k
l
=
где
где
–
–
линейный
линейный
масштаб
масштаб
;
;
и
и
–
–
геометрические
геометрические
размеры
размеры
натуры
натуры
и
и
модели
модели
.
.
l
k
н
l
м
l
н
S
м
S
k
S
=
н
V
м
V
k
V
=
-
-
масштаб
масштаб
площадей
площадей
-
-
масштаб
масштаб
объемов
объемов

Виды
Виды
подобия
подобия
.
.
Масштабы
Масштабы
моделирования
моделирования
Кинематическими
Кинематическими
подобными
подобными
являются
являются
два
два
потока
потока
,
,
если
если
поля
поля
скоростей
скоростей
на
на
модели
модели
и
и
в
в
натуре
натуре
в
в
подобных
подобных
точках
точках
пространства
пространства
связаны
связаны
масштабом
масштабом
н
м
k
υ
υ
=
υ
н
a
м
a
k
a
=
-
-
масштаб
масштаб
ускорений
ускорений
Для
Для
динамического
динамического
подобия
подобия
необходимо
необходимо
,
,
чтобы
чтобы
все
все
силы
силы
одинаковой
одинаковой
природы
природы
,
,
действующие
действующие
в
в
подобных
подобных
точках
точках
модели
модели
и
и
натуры
натуры
на
на
частицы
частицы
жидкости
жидкости
,
,
отличались
отличались
между
между
собой
собой
только
только
постоянными
постоянными
масштабами
масштабами
н
F
м
F
k
F
=
масштаб
масштаб
сил
сил
можно
можно
представить
представить
следующими
следующими
выражениями
выражениями
322
Fam V l l
tt
kk
k kk kk kk kkk
kk
νν
ρ
ρνρ
== = =

Критерии
Критерии
подобия
подобия
Устанавливаемые
Устанавливаемые
частные
частные
условия
условия
подобия
подобия
называются
называются
критериями
критериями
подобия
подобия
.
.
Критерий
Критерий
Эйлера
Эйлера
.
.
22
нм
нн мм
pp
uu
=
ρρ
2
Eu
p
idem
u
==
ρ
термин
термин
idem
idem
означает
означает
,
,
что
что
условия
условия
,
,
определяемые
определяемые
данным
данным
соотношением
соотношением
,
,
должны
должны
быть
быть
одинаковы
одинаковы
на
на
модели
модели
и
и
на
на
натуре
натуре
.
.
Вывод
Вывод
:
:
критерию
критерию
Эйлера
Эйлера
соответствует
соответствует
равенство
равенство
отношений
отношений
сил
сил
давления
давления
к
к
силам
силам
инерции
инерции
на
на
модели
модели
и
и
на
на
натуре
натуре
.
.
Критерий
Критерий
Рейнольдса
Рейнольдса
нн н мм м
нм
ul u l
ρ
ρ
=
μμ
Re
ul
idem
ρ
==
μ
При
При
соблюдении
соблюдении
критерия
критерия
Рейнольдса
Рейнольдса
критерий
критерий
Эйлера
Эйлера
выполняется
выполняется
автоматически
автоматически
.
.
Если
Если
жидкости
жидкости
на
на
модели
модели
и
и
в
в
натуре
натуре
одинаковы
одинаковы
,
,
то
то
при
при
равенстве
равенстве
Re Re
нм
=
нн мм
ul u l
=
1
l
u
k
k
=
Вывод
Вывод
:
:
При
При
моделировании
моделировании
по
по
Рейнальдсу
Рейнальдсу
уменьшение
уменьшение
размеров
размеров
модели
модели
в
в
раз
раз
требует
требует
увеличения
увеличения
скорости
скорости
движения
движения
жидкости
жидкости
на
на
модели
модели
в
в
такое
такое
же
же
количество
количество
раз
раз
.
.
Критерий
Критерий
Фруда
Фруда
Критерии
Критерии
подобия
подобия
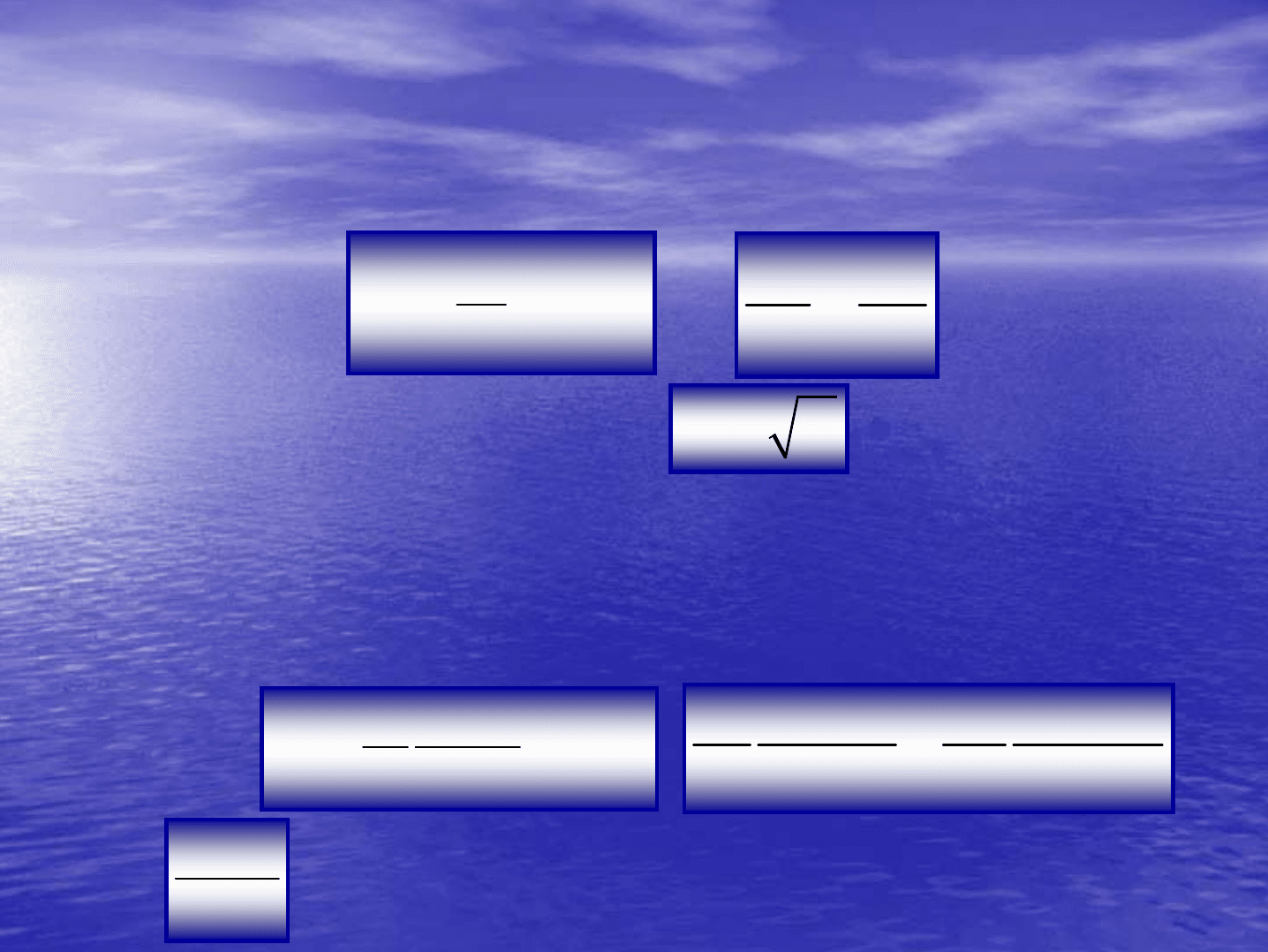
2
u
F
ridem
gl
==
22
нм
нм
uu
gl gl
=
При
При
моделировании
моделировании
по
по
Фруду
Фруду
ul
kk=
Вывод
Вывод
:
:
Одновременно
Одновременно
нельзя
нельзя
удовлетворить
удовлетворить
равенство
равенство
критериев
критериев
Рейнольдса
Рейнольдса
и
и
Фруда
Фруда
для
для
одной
одной
и
и
той
той
же
же
жидкости
жидкости
на
на
модели
модели
и
и
в
в
натуре
натуре
.
.
Критерий
Критерий
Архимеда
Архимеда
Определяет
Определяет
отношение
отношение
выталкивающей
выталкивающей
силы
силы
Архимеда
Архимеда
к
к
силам
силам
инерции
инерции
Определяет
Определяет
отношение
отношение
сил
сил
инерции
инерции
к
к
силам
силам
тяжести
тяжести
0
2
gl
A
ridem
u
ρ
−ρ
==
ρ
00
22
нн н мм м
нн м м
gl gl
uu
ρ
−ρ ρ −ρ
=
ρρ
0
ρ
−ρ
ρ
где
где
–
–
отношение
отношение
разности
разности
плотностей
плотностей
среды
среды
и
и
струи
струи
к
к
плотности
плотности
среды
среды
.
.
