Презентация - Калинин А.В., Лушкин И.А. Гидравлика
Подождите немного. Документ загружается.


Расчет
Расчет
длинных
длинных
трубопроводов
трубопроводов
Понятие
Понятие
о
о
простом
простом
и
и
сложном
сложном
напорных
напорных
трубопроводах
трубопроводах
При
При
расчете
расчете
длинных
длинных
трубопроводов
трубопроводов
пренебрегают
пренебрегают
потерями
потерями
напора
напора
на
на
местных
местных
сопротивлениях
сопротивлениях
,
,
которые
которые
малы
малы
и
и
обычно
обычно
не
не
превышают
превышают
5
5
%
%
от
от
общих
общих
потерь
потерь
.
.
Преобразуем
Преобразуем
формулу
формулу
Дарси
Дарси
,
,
заменив
заменив
скорость
скорость
расходом
расходом
,
,
поделенным
поделенным
на
на
площадь
площадь
поперечного
поперечного
сечения
сечения
трубы
трубы
lAQ
d
g
Q
d
l
gd
l
h
2
2
2
2
2
ср
дл
4
2
2
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
π
λ=
υ
λ=
52
8
dg
A
π
λ
=
–
–
удельное
удельное
сопротивление
сопротивление
трубопровода
трубопровода
Величина
Величина
А
К
1
=
называется
называется
модулем
модулем
расхода
расхода
и
и
также
также
приводится
приводится
в
в
справочниках
справочниках
.
.
Тогда
Тогда
l
K
Q
h
2
2
дл
=

Понятие
Понятие
о
о
простом
простом
и
и
сложном
сложном
напорных
напорных
трубопроводах
трубопроводах
Запишем
Запишем
уравнение
уравнение
Бернулли
Бернулли
для
для
двух
двух
сечений
сечений
трубопровода
трубопровода
в
в
его
его
начале
начале
и
и
в
в
конце
конце
:
:
дл
ср
2
22
2
2
ср
2
11
1
1
22
h
gg
p
z
gg
p
z +
υα
+
ρ
+=
υα
+
ρ
+
Обозначим
Обозначим
:
:
тр
1
H
g
p
=
ρ
–
–
требуемый
требуемый
напор
напор
,
,
т
т
.
.
е
е
.
.
напор
напор
,
,
который
который
должен
должен
создать
создать
насос
насос
в
в
начале
начале
трубопровода
трубопровода
;
;
zzz Δ
=
−
12
–
–
разность
разность
отметок
отметок
земли
земли
в
в
конце
конце
и
и
в
в
начале
начале
трубопровода
трубопровода
;
;
п
2
H
g
p
=
ρ
–
–
пьезометрический
пьезометрический
напор
напор
,
,
т
т
.
.
е
е
.
.
напор
напор
в
в
конце
конце
трубопровода
трубопровода
,
,
который
который
задается
задается
при
при
проектировании
проектировании
;
;
стп
HzH
=
Δ
+
–
–
статический
статический
напор
напор
.
.
Принимая
Принимая
во
во
внимание
внимание
,
,
что
что
в
в
трубопроводе
трубопроводе
постоянного
постоянного
диаметра
диаметра
gg 22
ср
2
22
ср
2
11
υα
=
υα
уравнение
уравнение
Бернулли
Бернулли
примет
примет
вид
вид
l
K
Q
НH
2
2
сттр
+=
Простым
Простым
называется
называется
трубопровод
трубопровод
,
,
не
не
имеющий
имеющий
ответвлений
ответвлений
.
.
Всякие
Всякие
другие
другие
трубопроводы
трубопроводы
относят
относят
к
к
категории
категории
сложных
сложных
.
.
Расчет
Расчет
трубопроводов
трубопроводов
,
,
соединенных
соединенных
последовательно
последовательно
и
и
параллельно
параллельно
l
1
l
2
l
3
d
2
d
1
d
3
Q
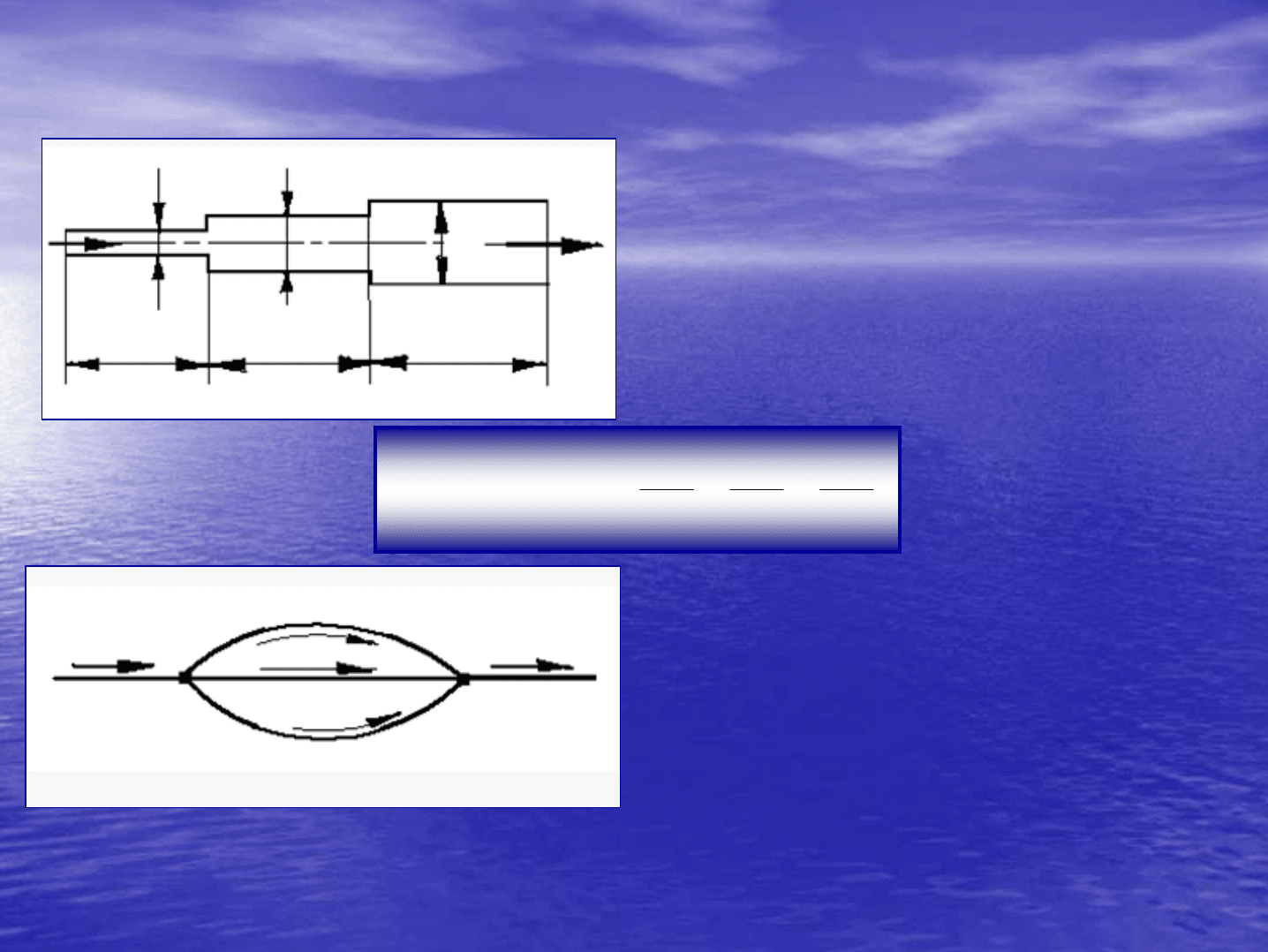
При
При
последовательном
последовательном
соединении
соединении
простых
простых
трубопроводов
трубопроводов
разной
разной
длины
длины
и
и
с
с
различными
различными
диаметрами
диаметрами
стык
стык
в
в
стык
стык
,
,
трубопровод
трубопровод
представляет
представляет
собой
собой
простой
простой
трубопровод
трубопровод
,
,
который
который
можно
можно
разделить
разделить
на
на
несколько
несколько
участко
участко
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+++=
2
3
3
2
2
2
2
1
1
2
сттр
K
l
K
l
K
l
QНH
l
1
l
2
l
3
d
2
d
1
d
3
Q
Q
1
Q
2
Q
3
Q
A
B
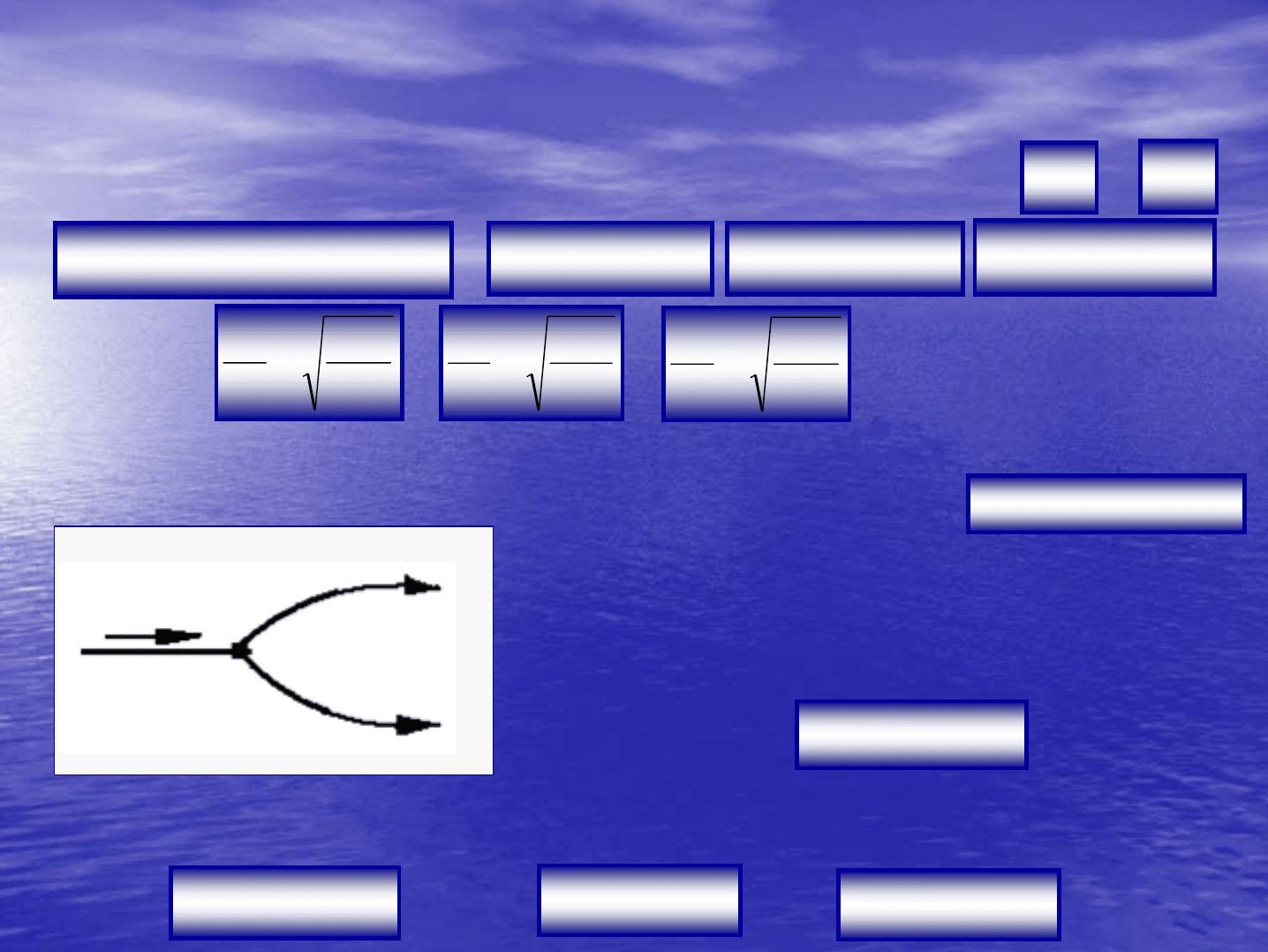
При
При
параллельном
параллельном
соединении
соединении
пьезометрический
пьезометрический
напор
напор
в
в
узловых
узловых
точках
точках
А
А
и
и
В
В
одинаков
одинаков
для
для
всех
всех
участков
участков
.
.
Расход
Расход
Q
Q
основного
основного
трубопровода
трубопровода
до
до
деления
деления
и
и
после
после
объединения
объединения
труб
труб
один
один
и
и
тот
тот
же
же
.
.
Задача
Задача
расчета
расчета
состоит
состоит
в
в
том
том
,
,
чтобы
чтобы
определить
определить
расходы
расходы
в
в
отдельных
отдельных
ветвях
ветвях
системы
системы
и
и
также
также
потери
потери
напора
напора
между
между
точками
точками
А
А
и
и
В
В
.
.
Общий
Общий
расход
расход
,
,
диаметры
диаметры
и
и
длины
длины
труб
труб
предполагаются
предполагаются
известными
известными
.
.
Расчет
Расчет
трубопроводов
трубопроводов
,
,
соединенных
соединенных
последовательно
последовательно
и
и
параллельно
параллельно
Потери
Потери
напора
напора
в
в
любой
любой
трубе
трубе
ответвления
ответвления
одинаковы
одинаковы
,
,
так
так
как
как
в
в
обеих
обеих
общих
общих
точках
точках
разветвления
разветвления
имеется
имеется
один
один
и
и
тот
тот
же
же
напор
напор
и
и
А
Н
В
Н
дл32дл1длдл
hhhh
=
=
=
1
2
111дл
lQAh =
2
2
22дл2
lQAh =
3
2
33дл3
lQAh =
Отсюда
Отсюда
11
22
2
1
lA
lA
Q
Q
=
11
33
3
1
lA
lA
Q
Q
=
22
33
3
2
lA
lA
Q
Q
=
,
,
т
т
.
.
е
е
.
.
расходы
расходы
на
на
участках
участках
распределяются
распределяются
обратно
обратно
пропорционально
пропорционально
корню
корню
квадратному
квадратному
из
из
их
их
сопротивлений
сопротивлений
.
.
Кроме
Кроме
того
того
321
QQQQ
+
+
=
l
1
l
2
d
2
d
1
Q
Q
1
Q
2
A B
D
С
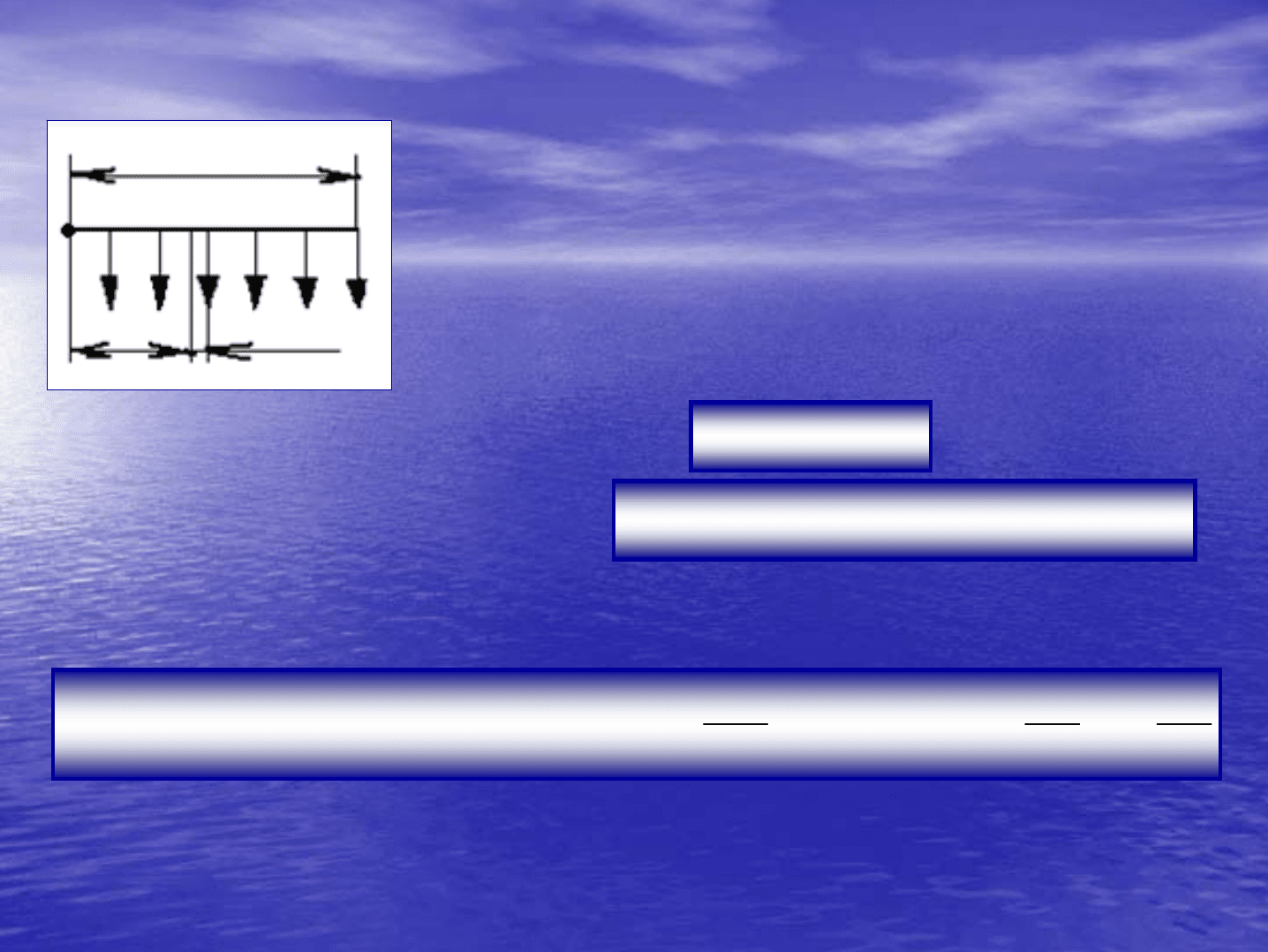
Простое
Простое
разветвление
разветвление
представляет
представляет
собой
собой
схему
схему
так
так
называемой
называемой
«
«
вилки
вилки
»
»
.
.
В
В
отличие
отличие
от
от
параллельного
параллельного
соединения
соединения
напоры
напоры
в
в
конечных
конечных
точках
точках
С
С
и
и
D
D
могут
могут
быть
быть
не
не
одинаковы
одинаковы
.
.
21
QQQ
+
=
Для
Для
определения
определения
расходов
расходов
в
в
ветвях
ветвях
при
при
заданном
заданном
общем
общем
расходе
расходе
и
и
размерах
размерах
труб
труб
ветвей
ветвей
необходимо
необходимо
составить
составить
уравнения
уравнения
lАQh
АВ
2
дл
=
1
2
111
lQАh =
2
2
222
lQАh =
,
,
,
,
Расчет
Расчет
трубопроводов
трубопроводов
,
,
соединенных
соединенных
последовательно
последовательно
и
и
параллельно
параллельно
dx
x
l
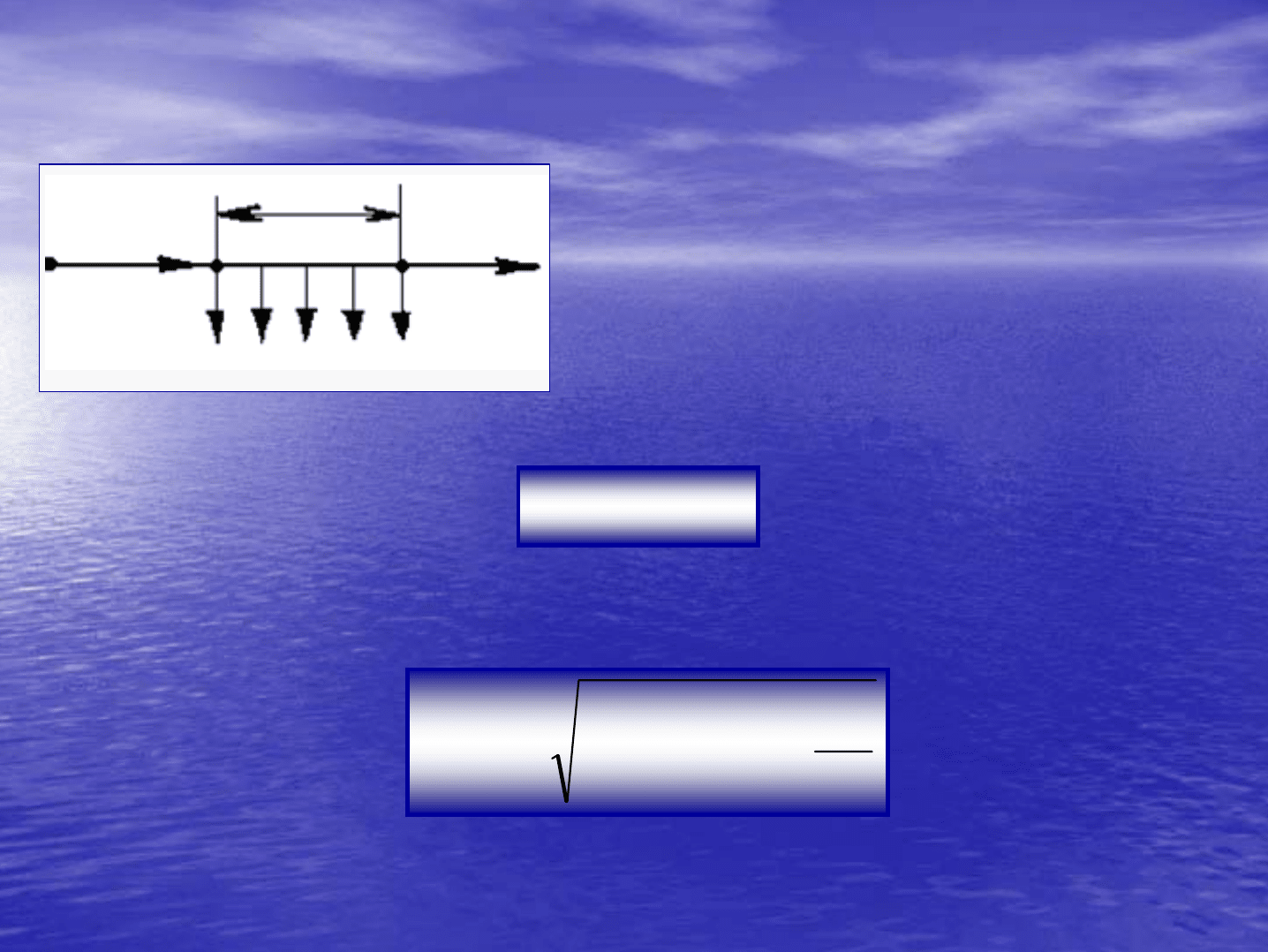
Непрерывная
Непрерывная
раздача
раздача
расхода
расхода
по
по
пути
пути
.
.
К
К
такой
такой
схеме
схеме
приближается
приближается
работа
работа
магистрали
магистрали
водопроводной
водопроводной
сети
сети
вдоль
вдоль
улицы
улицы
города
города
при
при
правильной
правильной
планировке
планировке
поперечных
поперечных
улиц
улиц
.
.
Возьмем
Возьмем
элементарный
элементарный
участок
участок
dx
dx
на
на
расстоянии
расстоянии
х
х
от
от
начала
начала
трубопровода
трубопровода
.
.
Разбор
Разбор
расхода
расхода
на
на
1
1
м
м
длины
длины
–
–
q
q
.
.
Расход
Расход
через
через
элементарный
элементарный
участок
участок
qxQQ
x
−
=
Потеря
Потеря
напора
напора
на
на
этом
этом
участке
участке
dxqxQAdxАQdh
x
2
2
дл
)( −==
Потеря
Потеря
напора
напора
по
по
всей
всей
длине
длине
трубопровода
трубопровода
333
)(
22
22
32
22
00
2
lQ
A
lQ
lQlQA
lq
QqllQAdxqxQАdhh
ll
длдл
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−=−==
∫∫
Вывод
Вывод
:
:
При
При
равномерной
равномерной
раздаче
раздаче
потеря
потеря
энергии
энергии
в
в
трубопроводе
трубопроводе
в
в
три
три
раза
раза
меньше
меньше
,
,
чем
чем
в
в
случае
случае
транзитного
транзитного
расхода
расхода
.
.
Расчет
Расчет
трубопроводов
трубопроводов
,
,
соединенных
соединенных
последовательно
последовательно
и
и
параллельно
параллельно
Q
т
+Q
р
Q
р
Q
т
l
На
На
практике
практике
обычно
обычно
встречается
встречается
смешанный
смешанный
случай
случай
,
,
когда
когда
часть
часть
расхода
расхода
проходит
проходит
транзитом
транзитом
,
,
а
а
другая
другая
отбирается
отбирается
вдоль
вдоль
пути
пути
В
В
этом
этом
случае
случае
потеря
потеря
напора
напора
определяется
определяется
по
по
формуле
формуле
lАQh
2
расчдл
=
Расчетный
Расчетный
расход
расход
3
2
p
тp
2
трасч
Q
QQQQ ++=
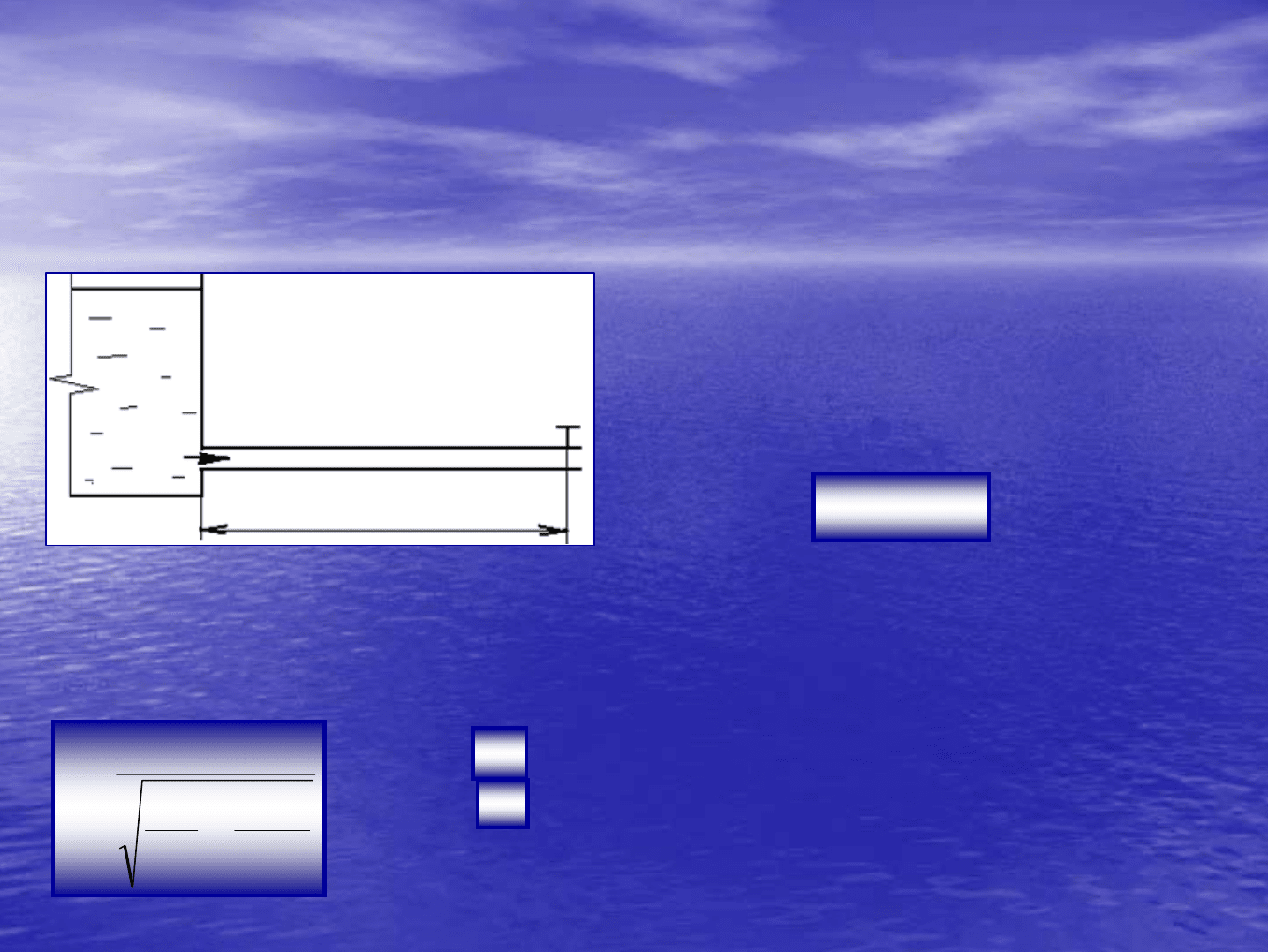
Гидравлический
Гидравлический
удар
удар
Под
Под
гидравлическим
гидравлическим
ударом
ударом
понимают
понимают
резкое
резкое
повышение
повышение
давления
давления
жидкости
жидкости
в
в
трубопроводе
трубопроводе
,
,
вызванное
вызванное
внезапным
внезапным
изменением
изменением
скорости
скорости
течения
течения
.
.
Явление
Явление
гидравлического
гидравлического
удара
удара
свойственно
свойственно
только
только
капельным
капельным
жидкостям
жидкостям
,
,
которые
которые
почти
почти
не
не
деформируются
деформируются
.
.
υ
0
А
В
l
Теоретическое
Теоретическое
обоснование
обоснование
явления
явления
гидравлического
гидравлического
удара
удара
и
и
метод
метод
его
его
расчета
расчета
впервые
впервые
дал
дал
Н
Н
.
.
Е
Е
.
.
Жуковский
Жуковский
в
в
1898
1898
г
г
.
.
Жуковский
Жуковский
предложил
предложил
формулу
формулу
для
для
определения
определения
повышения
повышения
давления
давления
,
,
применив
применив
закон
закон
сохранения
сохранения
количества
количества
движения
движения
0уд
υ
ρ
=
Δ
cp
где
где
с
с
–
–
скорость
скорость
распространения
распространения
гидравлического
гидравлического
удара
удара
вдоль
вдоль
трубы
трубы
от
от
крана
крана
до
до
резервуара
резервуара
.
.
Скорость
Скорость
распространения
распространения
гидравлического
гидравлического
удара
удара
можно
можно
найти
найти
,
,
применив
применив
закон
закон
сохранения
сохранения
массы
массы
с
с
учетом
учетом
уравнений
уравнений
механики
механики
упругих
упругих
тел
тел
трж
21
1
E
r
E
с
δ
ρ
+
=
где
где
–
–
модуль
модуль
упругости
упругости
жидкости
жидкости
;
;
–
–
модуль
модуль
упругости
упругости
трубы
трубы
;
;
r
r
–
–
радиус
радиус
трубы
трубы
;
;
δ
δ
–
–
толщина
толщина
стенки
стенки
трубы
трубы
.
.
ж
Е
тр
Е
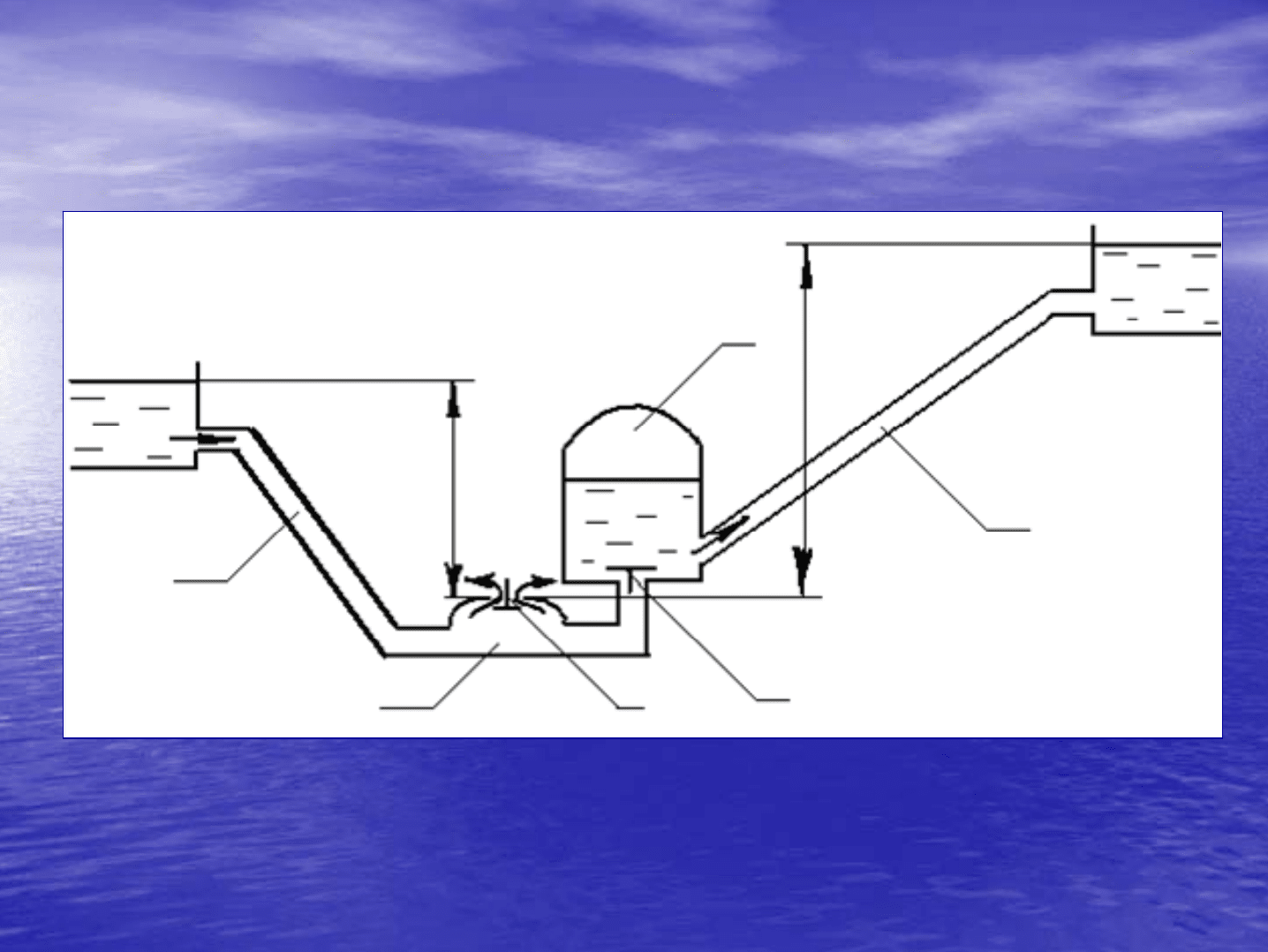
Гидравлический
Гидравлический
таран
таран
Гидравлический
Гидравлический
таран
таран
служит
служит
для
для
подачи
подачи
воды
воды
на
на
небольшую
небольшую
высоту
высоту
без
без
использования
использования
насосов
насосов
.
.
1
2
3
4
5
6
H
2
H
1
Таким
Таким
образом
образом
,
,
гидравлический
гидравлический
таран
таран
затрачивает
затрачивает
часть
часть
расхода
расхода
на
на
подъем
подъем
воды
воды
по
по
нагнетательному
нагнетательному
трубопроводу
трубопроводу
на
на
высоту
высоту
,
,
которая
которая
может
может
достигать
достигать
10
10
H
H
1
1
.
.
Обычно
Обычно
теряется
теряется
половина
половина
расхода
расхода
.
.
