Презентация - Калинин А.В., Лушкин И.А. Гидравлика
Подождите немного. Документ загружается.


Конечно
Конечно
-
-
разностная
разностная
форма
форма
уравнения
уравнения
Навье
Навье
-
-
Стокса
Стокса
Напряженное
Напряженное
состояние
состояние
жидкости
жидкости
.
.
Законы
Законы
движения
движения
и
и
покоя
покоя
жидкостей
жидкостей
и
и
газов
газов
основываются
основываются
на
на
законах
законах
механики
механики
сплошной
сплошной
среды
среды
,
,
что
что
позволяет
позволяет
рассматривать
рассматривать
равновесие
равновесие
и
и
течение
течение
жидкости
жидкости
в
в
целом
целом
без
без
учета
учета
механизма
механизма
молекулярного
молекулярного
движения
движения
.
.
σ
2
σ
1
σ
3
τ
1
τ
1
τ
3
τ
2
τ
2
τ
2
τ
1
τ
3
τ
3
z
z
′
y
y
′
x
x
′
На
На
поверхности
поверхности
граней
граней
элементарного
элементарного
параллелепипеда
параллелепипеда
возникают
возникают
три
три
различных
различных
по
по
величине
величине
касательных
касательных
напряжения
напряжения
и
и
три
три
нормальных
нормальных
составляющих
составляющих
напряжений
напряжений
:
:
вдоль
вдоль
осей
осей
x
x
и
и
y
y
–
–
напряжение
напряжение
τ
τ
1
1
,
,
вдоль
вдоль
осей
осей
x
x
и
и
z
z
–
–
τ
τ
2
2
и
и
вдоль
вдоль
осей
осей
y
y
и
и
z
z
–
–
τ
τ
3
3
.
.
Вдоль
Вдоль
оси
оси
x
x
действует
действует
нормальна
нормальна
я
я
составляющая
составляющая
напряжения
напряжения
σ
σ
1,
1,
вдоль
вдоль
оси
оси
y
y
–
–
σ
σ
2
2
и
и
вдоль
вдоль
оси
оси
z
z
–
–
σ
σ
3
3
.
.
На
На
массу
массу
жидкости
жидкости
,
,
находящуюся
находящуюся
в
в
изолированном
изолированном
объеме
объеме
,
,
действуют
действуют
массовые
массовые
силы
силы
,
,
которые
которые
пропорциональны
пропорциональны
третьей
третьей
степени
степени
размера
размера
выделенного
выделенного
объема
объема

Конечно
Конечно
-
-
разностная
разностная
форма
форма
уравнения
уравнения
Навье
Навье
-
-
Стокса
Стокса
Суммарная
Суммарная
проекция
проекция
силы
силы
,
,
определяемая
определяемая
нормальными
нормальными
составляющими
составляющими
напряжения
напряжения
()
1
11 1
.
x
dx d
y
dz d
y
dz dxd
y
dz
x
∂
σ
σ+∂σ ∂ −σ =
⎡⎤
⎣⎦
∂
Составляющие
Составляющие
вдоль
вдоль
оси
оси
х
х
3
dxdydz
y
∂
τ
∂
2
dxd
y
dz
y
∂
τ
∂
Суммарная
Суммарная
составляющая
составляющая
сил
сил
,
,
возникающих
возникающих
на
на
гранях
гранях
изолированного
изолированного
элемента
элемента
жидкости
жидкости
за
за
счет
счет
дополнительного
дополнительного
напряжения
напряжения
в
в
проекции
проекции
на
на
ось
ось
x
x
,
,
равна
равна
3
12
dxdydz
xyz
⎛⎞
∂τ
∂σ ∂τ
++
⎜⎟
∂∂∂
⎝⎠
Аналогично
Аналогично
составляющие
составляющие
дополнительного
дополнительного
напряжения
напряжения
,
,
действующие
действующие
на
на
остальных
остальных
гранях
гранях
,
,
в
в
проекциях
проекциях
на
на
оси
оси
0
0
y
y
и
и
0
0
z
z
дадут
дадут
составляющие
составляющие
сил
сил
:
:
3
21
dxdydz
yxz
⎛⎞
∂τ
∂σ ∂τ
++
⎜⎟
∂∂∂
⎝⎠
3
12
dxdydz
zyx
⎛⎞
∂σ
∂τ ∂τ
++
⎜⎟
∂∂∂
⎝⎠
и
и

Конечно
Конечно
-
-
разностная
разностная
форма
форма
уравнения
уравнения
Навье
Навье
-
-
Стокса
Стокса
Прибавляя
Прибавляя
эти
эти
силы
силы
,
,
отнесенные
отнесенные
к
к
единице
единице
массы
массы
жидкости
жидкости
к
к
правой
правой
части
части
уравнений
уравнений
Эйлера
Эйлера
,
,
получим
получим
условия
условия
динамического
динамического
равновесия
равновесия
в
в
точке
точке
потока
потока
при
при
течении
течении
реальной
реальной
жидкости
жидкости
3
12
3
21
3
1
11
;
11
;
11
xxxx
xyz
yyyy
xyz
zzzz
xyz
uuuu
p
u u u X dxdydz
ttyz x xyz
uuuu
p
u u u Y dxdydz
ttyz y yxz
uuuu
p
uuu Z
ttyz y zy
⎛⎞
∂∂∂∂ ∂τ
∂σ ∂τ
∂
+++=−++ ++
⎜⎟
∂ ∂ ∂ ∂ ρ∂ ρ∂∂∂
⎝⎠
∂∂∂∂
⎛⎞
∂τ
∂σ ∂τ
∂
+++=−++ ++
⎜⎟
∂∂∂∂ρ∂ρ∂∂∂
⎝⎠
∂σ
∂ ∂ ∂ ∂ ∂τ ∂τ
∂
+++=−++ ++
∂∂∂∂ρ∂ ρ∂∂
2
.dxdydz
x
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎛⎞
⎪
⎜⎟
∂
⎪
⎝⎠
⎭
Определим
Определим
теперь
теперь
силы
силы
,
,
возникающие
возникающие
в
в
точке
точке
потока
потока
за
за
счет
счет
вязкости
вязкости
.
.
Проекция
Проекция
на
на
ось
ось
0
0
x
x
сил
сил
вязкости
вязкости
,
,
отнесенных
отнесенных
к
к
единице
единице
объема
объема
и
и
действующих
действующих
в
в
точке
точке
,
,
определяемой
определяемой
в
в
потоке
потоке
координатами
координатами
x
x
,
,
y
y
,
,
z
z
:
:
2
3
12
2
2
y
xxx
z
u
uuu
u
x
yz x yxy zzy
⎡
∂⎤
⎛⎞
⎛⎞
∂τ ∂ ∂ ∂
∂σ ∂τ ∂
∂∂
+++μ + + + +
⎢
⎥
⎜⎟
⎜⎟
∂∂∂ ∂ ∂∂∂ ∂∂∂
⎝⎠
⎝⎠
⎣
⎦

Конечно
Конечно
-
-
разностная
разностная
форма
форма
уравнения
уравнения
Навье
Навье
-
-
Стокса
Стокса
Дифференцируя
Дифференцируя
уравнение
уравнение
неразрывности
неразрывности
по
по
x
x
,
,
получим
получим
0
x
zz
u
uu
xx y z
⎛⎞
∂
∂∂
∂
++ =
⎜⎟
∂∂ ∂ ∂
⎝⎠
.
y
x
z
u
u
u
xx xy z
∂
⎛⎞
∂
∂
∂∂
⎛⎞
=− +
⎜⎟
⎜⎟
∂∂ ∂∂ ∂
⎝⎠
⎝⎠
или
или
Тогда
Тогда
уравнение
уравнение
сил
сил
,
,
возникающих
возникающих
за
за
счет
счет
вязкости
вязкости
жидкости
жидкости
,
,
равно
равно
222
222
x
xx
uuu
x
yz
⎛⎞
∂∂∂
μ++
⎜⎟
∂∂∂
⎝⎠
Аналогично
Аналогично
в
в
проекции
проекции
на
на
оси
оси
0
0
y
y
и
и
0
0
z
z
дополнительная
дополнительная
проекция
проекция
сил
сил
,
,
которые
которые
следует
следует
учитывать
учитывать
при
при
течении
течении
вязких
вязких
жидкостей
жидкостей
,
,
составит
составит
:
:
222
222
yyy
uuu
xyz
⎛⎞
∂∂∂
μ++
⎜⎟
⎜⎟
∂∂∂
⎝⎠
222
222
.
zzz
uuu
xyz
⎛⎞
∂∂∂
μ++
⎜⎟
∂∂∂
⎝⎠
и
и

Конечно
Конечно
-
-
разностная
разностная
форма
форма
уравнения
уравнения
Навье
Навье
-
-
Стокса
Стокса
Уравнения
Уравнения
Эйлера
Эйлера
с
с
учетом
учетом
этих
этих
дополнительных
дополнительных
сил
сил
примут
примут
вид
вид
:
:
222
222
222
222
22
2
1
;
1
;
1
x x x x xxx
xyz
y y y y yyy
xyz
zzzz zz
xyz
uuuu uuu
p
uuu X
ttyz x xyz
u u u u uuu
p
uuu Y
ttyz y xyz
uuuu uu
p
uuu Z
ttyz y x
⎛⎞
∂∂∂∂ ∂∂∂
∂μ
+++=−++ ++
⎜⎟
∂∂∂∂ρ∂ ρ∂∂∂
⎝⎠
⎛⎞
∂ ∂ ∂ ∂ ∂∂∂
∂μ
+++=−++ ++
⎜⎟
⎜⎟
∂∂∂∂ρ∂ρ∂∂∂
⎝⎠
∂∂∂∂ ∂∂
∂μ
+++=−++ +
∂∂∂∂ρ∂ ρ∂
2
22
.
z
u
yz
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎛⎞
∂
⎪
+
⎜⎟
⎪
∂∂
⎝⎠
⎭
Полученная
Полученная
система
система
уравнений
уравнений
называется
называется
уравнениями
уравнениями
Навье
Навье
-
-
Стокса
Стокса
.
.
Уравнение
Уравнение
Навье
Навье
-
-
Стокса
Стокса
,
,
как
как
и
и
уравнение
уравнение
Зйлера
Зйлера
,
,
интегрируются
интегрируются
только
только
для
для
некоторых
некоторых
частных
частных
случаев
случаев
,
,
но
но
в
в
последние
последние
годы
годы
,
,
в
в
связи
связи
с
с
развитием
развитием
различных
различных
методов
методов
решения
решения
подобных
подобных
задач
задач
,
,
полученные
полученные
уравнения
уравнения
используются
используются
все
все
чаще
чаще
и
и
являются
являются
идеальным
идеальным
инструментом
инструментом
,
,
позволяющим
позволяющим
получить
получить
хороший
хороший
результат
результат
.
.
Наиболее
Наиболее
часто
часто
для
для
решения
решения
уравнений
уравнений
Навье
Навье
-
-
Стокса
Стокса
применяются
применяются
численные
численные
методы
методы
.
.

Общая
Общая
схема
схема
применения
применения
численных
численных
методов
методов
и
и
их
их
реализация
реализация
на
на
ЭВМ
ЭВМ
Под
Под
численными
численными
методами
методами
подразумеваются
подразумеваются
методы
методы
решения
решения
задач
задач
,
,
сводящиеся
сводящиеся
к
к
арифметическим
арифметическим
и
и
логическим
логическим
действиям
действиям
над
над
числами
числами
,
,
т
т
.
.
е
е
.
.
к
к
тем
тем
действиям
действиям
,
,
которые
которые
выполняет
выполняет
ЭВМ
ЭВМ
.
.
Решение
Решение
,
,
полученное
полученное
численным
численным
методом
методом
,
,
обычно
обычно
является
является
приближенным
приближенным
,
,
т
т
.
.
е
е
.
.
содержит
содержит
некоторую
некоторую
погрешность
погрешность
.
.
Источниками
Источниками
погрешности
погрешности
являются
являются
:
:
1)
1)
несоответствие
несоответствие
математической
математической
задачи
задачи
изучаемому
изучаемому
реальному
реальному
явлению
явлению
;
;
2)
2)
погрешность
погрешность
исходных
исходных
данных
данных
;
;
3)
3)
погрешность
погрешность
метода
метода
решения
решения
;
;
4)
4)
ошибки
ошибки
округлений
округлений
в
в
арифметических
арифметических
и
и
других
других
действиях
действиях
над
над
числами
числами
.
.
Погрешность
Погрешность
в
в
решении
решении
,
,
обусловленная
обусловленная
первыми
первыми
двумя
двумя
источниками
источниками
называется
называется
неустранимой
неустранимой
.
.
Численные
Численные
методы
методы
в
в
большинстве
большинстве
случаев
случаев
сами
сами
по
по
себе
себе
являются
являются
приближенными
приближенными
.
.
Такие
Такие
погрешности
погрешности
называются
называются
погрешностями
погрешностями
метода
метода
.
.

Общая
Общая
схема
схема
применения
применения
численных
численных
методов
методов
и
и
их
их
реализация
реализация
на
на
ЭВМ
ЭВМ
При
При
решении
решении
задач
задач
на
на
ЭВМ
ЭВМ
чаще
чаще
всего
всего
встречаются
встречаются
две
две
ситуации
ситуации
:
:
1)
1)
если
если
количество
количество
выполняемых
выполняемых
арифметических
арифметических
действий
действий
невелико
невелико
,
,
то
то
,
,
обычно
обычно
,
,
ошибки
ошибки
округления
округления
не
не
проявляются
проявляются
,
,
так
так
как
как
в
в
ЭВМ
ЭВМ
числа
числа
представляются
представляются
с
с
10
10
и
и
более
более
десятичными
десятичными
значащими
значащими
цифрами
цифрами
,
,
а
а
окончательный
окончательный
результат
результат
редко
редко
бывает
бывает
нужен
нужен
более
более
чем
чем
с
с
5
5
десятичными
десятичными
значащими
значащими
цифрами
цифрами
.
.
2)
2)
если
если
задача
задача
сложная
сложная
(
(
уравнения
уравнения
с
с
частными
частными
производными
производными
),
),
то
то
в
в
этом
этом
случае
случае
погрешности
погрешности
округления
округления
в
в
каждом
каждом
действии
действии
не
не
учитываются
учитываются
,
,
так
так
как
как
они
они
взаимокомпенсируются
взаимокомпенсируются
.
.
Численный
Численный
метод
метод
может
может
считаться
считаться
удачно
удачно
выбранным
выбранным
,
,
если
если
его
его
погрешность
погрешность
в
в
несколько
несколько
раз
раз
меньше
меньше
неустранимой
неустранимой
погрешности
погрешности
,
,
а
а
погрешность
погрешность
,
,
возникающая
возникающая
за
за
счет
счет
округлений
округлений
,
,
называемая
называемая
вычисленной
вычисленной
погрешностью
погрешностью
,
,
в
в
несколько
несколько
раз
раз
меньше
меньше
погрешности
погрешности
метода
метода
.
.

Общая
Общая
схема
схема
применения
применения
численных
численны
х
методов
методов
и
и
их
их
реализация
реализация
на
на
ЭВМ
ЭВМ
Этапы
Этапы
метода
метода
вычислительного
вычислительного
эксперимента
эксперимента
:
:
1.
1.
Формируется
Формируется
задача
задача
,
,
выбирается
выбирается
физическая
физическая
модель
модель
процесса
процесса
,
,
решается
решается
вопрос
вопрос
о
о
том
том
,
,
какие
какие
физические
физические
величины
величины
надо
надо
учитывать
учитывать
.
.
Проводится
Проводится
описание
описание
физической
физической
модели
модели
математическим
математическим
способом
способом
(
(
дифференциальные
дифференциальные
,
,
интегральные
интегральные
и
и
другие
другие
уравнения
уравнения
).
).
Полученную
Полученную
математическую
математическую
модель
модель
исследуют
исследуют
методами
методами
математической
математической
физики
физики
,
,
чтобы
чтобы
установить
установить
,
,
правильно
правильно
ли
ли
поставлена
поставлена
задача
задача
,
,
хватает
хватает
ли
ли
исходных
исходных
данных
данных
,
,
не
не
противоречат
противоречат
ли
ли
они
они
друг
друг
другу
другу
,
,
существует
существует
ли
ли
решение
решение
поставленной
поставленной
задачи
задачи
и
и
единственно
единственно
ли
ли
оно
оно
.
.
2.
2.
Построение
Построение
приближенного
приближенного
численного
численного
метода
метода
решения
решения
задачи
задачи
,
,
т
т
.
.
е
е
.
.
выбора
выбора
вычислительного
вычислительного
алгоритма
алгоритма
.
.
Вычислительный
Вычислительный
алгоритм
алгоритм
–
–
последовательность
последовательность
арифметических
арифметических
и
и
логических
логических
операций
операций
,
,
при
при
помощи
помощи
которых
которых
находится
находится
приближенное
приближенное
численное
численное
решение
решение
математической
математической
задачи
задачи
,
,
сформулированной
сформулированной
на
на
первом
первом
этапе
этапе
.
.
3.
3.
Программирование
Программирование
вычислительного
вычислительного
алгоритма
алгоритма
на
на
ЭВМ
ЭВМ
.
.
4.
4.
Проведение
Проведение
расчетов
расчетов
на
на
ЭВМ
ЭВМ
.
.
5.
5.
Анализ
Анализ
полученных
полученных
численных
численных
результатов
результатов
и
и
последующее
последующее
уточнение
уточнение
математической
математической
модели
модели
.
.
Измерительные
Измерительные
приборы
приборы
,
,
используемые
используемые
при
при
проведении
проведении
экспериментальных
экспериментальных
работ
работ
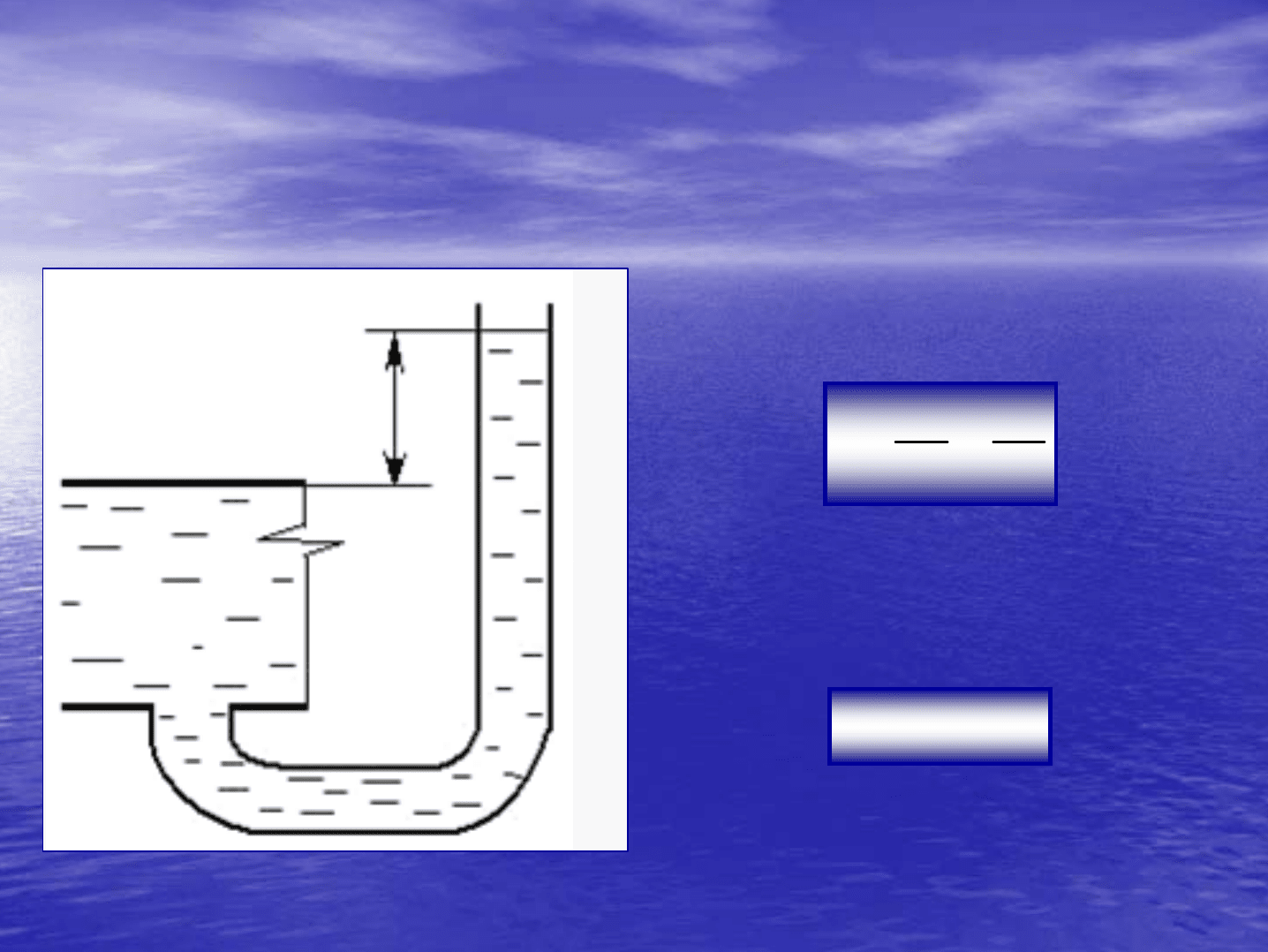
1.
1.
Жидкостные
Жидкостные
манометры
манометры
прямого
прямого
действия
действия
.
.
ΔH
A
B
Чувствительность
Чувствительность
манометра
манометра
определяется
определяется
по
по
следующей
следующей
формуле
формуле
1h
s
p
g
Δ
==
Δ
ρ
Давление
Давление
определяется
определяется
по
по
разности
разности
уровней
уровней
жидкости
жидкости
в
в
трубках
трубках
А
А
и
и
В
В
p
gh
=
ρΔ

Измерительные
Измерительные
приборы
приборы
,
,
используемые
используемые
при
при
проведении
проведении
экспериментальных
экспериментальных
работ
работ
2.
2.
Механические
Механические
манометры
манометры
.
.
T
C
B
p
Манометр
Манометр
состоит
состоит
из
из
согнутой
согнутой
металлической
металлической
трубки
трубки
Т
Т
,
,
один
один
конец
конец
которой
которой
соединен
соединен
с
с
резервуаром
резервуаром
,
,
в
в
котором
котором
измеряется
измеряется
давление
давление
.
.
Конец
Конец
трубки
трубки
В
В
соединен
соединен
с
с
рычагом
рычагом
ВС
ВС
,
,
который
который
поворачивает
поворачивает
стрелку
стрелку
.
.
При
При
повороте
повороте
стрелки
стрелки
она
она
указывает
указывает
величину
величину
давления
давления
.
.
При
При
избыточном
избыточном
давлении
давлении
в
в
трубке
трубке
Т
Т
свободный
свободный
ее
ее
конец
конец
В
В
начинает
начинает
распрямляться
распрямляться
и
и
приводит
приводит
в
в
движение
движение
стрелку
стрелку
,
,
которая
которая
показывает
показывает
величину
величину
давления
давления
.
.
Такие
Такие
манометры
манометры
отличаются
отличаются
прочностью
прочностью
.
.
