Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

dynamics is central. Hoskins et al. (1985), Salmon (1998), and Andrews et al. (1987)

are excellent starting points for further investigation.

 Rossby-Wave Dynamics The primary large-scale oscillations in the extra-

tropical atmosphere and oceans are Rossby waves, which are supported by the

PV gradients largely associated with planetary rotation. In the ‘‘billiard-ball

planet’’ example discussed in Section 2, it is Rossby waves that carry the signal

of the wave maker away from the equator. Rossby-wave dynamics underlies

our understanding of the midlatitude remote response to El Nin

o events in the

tropical Paciﬁc, of the propagation of upper tropospheric disturbances, and of

the dynamics of large-scale waves in the stratosphere (see Chapter 4).

 Baroclinic Instability The development of atmospheric cyclones and of

oceanic eddies can be understood in terms of the interactions of regions of

opposite-signed PV gradients (see Chapter 4).

 Geostrophic Turbulence Our understanding of atmosphere=ocean large-scale

turbulence is framed by PV, which behaves as an ‘‘active’’ tracer that can be

mixed and diffused downgradient (see Chapter 6).

 Balance Models Balance models, such as the quasi-geostrophic model

(Chapter 4, Swanson), are ﬁltered equations that model the slow, large-scale

motions associated with Rossby waves, baroclinic instability, and geostrophic

turbulence. These models are based on some of the dynamical regimes

mentioned above; for example, the assumption that the vertical component

of relative vorticity is small compared to the vertical component of planetary

vorticity. In these models, the PV is the sole dynamical variable, and all other

variables can be obtained from the PV by an inversion procedure. This

inversion procedure is analogous to the one involved in obtaining the circula-

tion from the vorticity distribution (see Section 2).

 Rossby-Wave Activity Propagation and Wave-Induced Circulations Recall

that the southward ﬂux of vorticity in the barotropic vorticity model example at

the end of Section 2 gives rise to a westward acceleration. More generally, the

ﬂux of PV in both the shallow-water model and ﬂuids with variable density can

be associated with a wave-induced torque, generally in the direction transverse

to the ﬂux. In this way, the existence of persistent extratropical jets, such as the

atmospheric jet stream and the jets in the Antarctic Circumpolar Current, can

be understood in terms of the ﬂux, often downgradient, of PV. These ﬂuxes are

also the starting point for a theory of ‘‘wave activity’’ propagation that is the

foundation of models of the overturning circulation in the stratosphere.

 Symmetries, Conservation Laws, and Hamiltonian Structure The existence

of PV as a constant of the motion has a profound connection to the math-

ematical structure of the equations of motion. All conserved quantities for a

physical system—spatially distributed quantities such as energy and momen-

tum, and local quantities such as PV and wave activity, are connected to

symmetries in the system through Noether’s theorem. This idea is the starting

point for Hamiltonian ﬂuid dynamics, which is reviewed in Salmon (1998).

The symmetry connected to the PV is the so-called particle relabeling

36 CIRCULATION, VORTICITY, AND POTENTIAL VORTICITY

symmetry, which reﬂects the fact that the dynamics of an adiabatic ﬂuid is

unaffected by changing the particle labels on isentropic surfaces. Such

considerations provide a theoretic al basis for wave activity invariants and

generalized nonlinear stability theorems for GFD, as well as for the systemat ic

derivation of balance models with desirable symmetry.

6 APPENDIX: MATHEMATICAL SUMMARY

In this section, we provide a summary, using the notation of vector calculus, of the

main results. First, the circulation, C, in statement 1, may be represented by a line

integral

C ¼

circuit

jujcos y ds

where u is the velocity measured from the inertial frame. In this notation, the length

of the circuit is L ¼

circuit

ds and the average of the tangential ﬂow component is

C=L. This is consistent with statement 1. By the Stokes theorem, the circulation also

satisﬁes

C ¼

ðð

region

curl u 

nn dA

where the double-integral sign and the word region indicate that a ﬂux integral is

being taken over the region bounded by the circuit, and

nn is a unit vector per pendi-

cular to the surface. The vector curl of the velocity is, in Cartesian coordinates,

curl u ¼



;



;





Statement 2 in the small-area limit implies that the vorticity, z, is equal to the curl

of the velocity:

z ¼ curl u

Statement 3 is therefore equivalent to the Stokes’s theorem for ﬁnite-area surfaces.

For the shallow-water system, the vorticity is vertical:

z ¼





6 APPENDIX: MATHEMATICAL SUMMARY 37

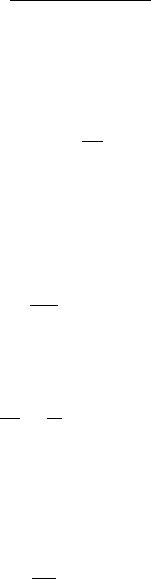
and the potential vorticity, statement 4, is

q ¼

ð@v=@xÞð@u=@yÞ

h  h

where h is the height of the ﬂuid surface and h

is the height of the solid surface

beneath the ﬂuid. Ertel’s PV, statement 5, is

q ¼ z 

where s is the speciﬁc entropy and r is the density.

The circulation theorem for the shallow-water model, statement 6, and Kelvin’s

circulation theorem, statement 8, are written

¼ 0

where D=Dt is the material derivative following the motion, deﬁned by

þ u  H

and C is the circulation of a material circuit. The conservation of PV following the

motion for shallow-water (statement 7) or three-dimensional stratiﬁed ﬂow (state-

ment 9) is

¼ 0

REFERENCES

Andrews, D. G., J. R. Holton, and C. B. Leovy (1987). Middle Atmosphere Dynamics , Orlando,

Academic.

Cotton, W. R., and R. A. Anthes (1989). Storm and cloud dynamics, San Diego, Academic.

Gill, A. E., (1982). Atmosphere-Ocean Dynamics, San Diego, Academic.

Holton, J. R. (1992). An Introduction to Dynamic Meteorology, 3rd Edition, San Diego,

Academic.

Hoskins, B. J., M. E. McIntyre, and A. W. Robertson (1985). On the use and signiﬁcance of

isentropic potential vorticity maps, Q. J. Roy. Met. Soc. 111, 877–946.

Kundu, P. K. (1990). Fluid Mechanics, San Diego, Academic.

Pedlosky, J. (1996). Ocean Circulation Theory, Berlin, Springer.

Salmon, (1998) Lectures on Geophysical Fluid Dynamics, New York, Oxford University Press.

CIRCULATION, VORTICITY, AND POTENTIAL VORTICITY

CHAPTER 4

EXTRATROPICAL ATMOSPHERIC

CIRCULATIONS

KYLE SWANSON

1 INTRODUCTION

As one moves poleward in Earth’s atmosphere, the character of the circulation

changes markedly. At large scales and low freque ncies, tropical circulations are

fundamentally ageostrophic, epitomized by the thermally direct Hadley, Walker,

and monsoon circulations. In contrast, at large scales and low frequencies in the

extratropics, the effect of Coriolis accelerations due to Earth’s rotation become

important, and circulations are approximately in geostrophic balance. As such,

away from the surface, the extratropical large-scale wind satisﬁes

ðu; v; wÞðu

; v

; 0Þba

1

c; ða cos fÞ

1

c; 0cð1Þ

where the geostrophic stream function is given by:

c  f

1

ðF  F

Þð2Þ

Here F

(z) is a suitable reference geopotential proﬁle and f

¼ 2O sin f

is the

Coriolis parameter evaluated at some extratropical latitude f

. The extent to which

geostrophic balance adequately describes the extratropical circulation is measured by

the smallness of the Rossby number, Ro ¼U=( f

L), which is approximately 0.1 for

velocity and length scales U 10 m= s and L 1000 km that, respectively, character-

ize large-scale extratropical dynamical mot ions.

Handbook of Weather, Climate, and Water: Dynamics, Climate, Physical Meteorology, Weather Systems,

and Measurements, Edited by Thomas D. Potter and Bradley R. Colman.

ISBN 0-471-21490-6 # 2003 John Wiley & Sons, Inc.

In addition to geostrophic balance, the extratropical atmospheric circulation is

also in hydrostatic balance. Hydrostatic balanc e provides a relation between the

potential temperature and mass ﬁelds of the form

 y  y

ðzÞ¼HR

1

kz=H

c ð3Þ

where y

ðzÞ¼HR

1

kz=H

is a reference potential temperature. The combina-

tion of hydrostatic and geostrophic balance, through cross differentiation of (1) and

(3), yields the thermal wi nd relations that link the vertical shear of the geostrophic

wind to horizontal potential temperature gradients. Therefore, the jets that dominate

the zonally averaged tropospheric ﬂow have their origin in the density contrasts of

the equator–pole temperature gradient and are referred to as baroclinic.

Approximate geostrophic balance, along with the existence of a robust zonally

averaged ﬂow provide the basis for theoretical inquiries into the dynamics of

observed large-scale motions in the extratropical atmosphere. The former allows

for a simpler description of the underlying dynamics, while the latter allows for

meaningful insights into dynamical phenomena to be gained through the study of

linear ﬂuctuations about a zonal basic state ﬂow. In this chapter, we apply these

simpliﬁcations to examine the dynamics of several important classes of large-scale

motions in the extratropical atmospheric circulation.

2 QUASI-GEOSTRO PHIC THEORY

Geostrophy by itself does not provide an adequate description of large-scale dyna-

mical motions, as it is a time-independent diagno stic relation between the mass and

velocity ﬁelds. To understand how ﬂows in approximate geostrophic balance evolve

in time, it is necessary to include the important effects of O(Ro) ageostrophic winds,

which includes the vertical wind. The quasi-geostrophic (QG) approximation

includes the effects of these ageostrophic winds on the O(1) geostrophic ﬁelds in

a simpliﬁed but consistent manner and provides a concise, idealized system with

which to study large-scale extratropical dynamical motions.

The QG approximation has its roots in the geometrical simpliﬁcation of replacing

the horizontal spherical coordinates (l , f) by the eastward and northward Cartesian

coordinates (x, y) in the full primitive equations and restricting the ﬂow domain to

some neighborhood of the latitude f

. Here x is eastward distance and y northward

distance from some origin (l

, f

). This geometric simpliﬁcation allows the QG

dynamical approximations to be made with full rigor (Pedlosky 1987, Section

6.2-5) and once made provides the important conceptual simpliﬁcation that the

only effect of Earth’s sphericity is the variation of the Coriolis parameter f with

latitude,

f ¼ f

þ by ð4Þ

40 EXTRATROPICAL ATMOSPHERIC CIRCULATIONS

where b ¼ 2Oa

1

cos f

. This so-called b-plane approximation captures the most

important dynamical effect of the variation of f with latitude. Once this simpliﬁcation

is made, the QG dynamical equations naturally emerge from an expansion of the

equations of motion in the small parameter Ro.

In the absence of forcing and dissipation,* QG dynamics are described by the

material conservation of quasi-geostrophic potential vorticity (QGPV) by the hori-

zontal geostrophic ﬂow

ð@

þ u

þ v

Þq ¼ 0 ð5Þ

where

q ¼ z

þ f

1

ð@y

=@zÞ

1

cþf

þ by

¼ @

c þ @

c þ r

1

ðr

cÞþf

þ by

ð6Þ

is the QGPV, z

is the vertical component of the relative geostrophic vorticity, and

eðzÞf

ðzÞ. QG dynamics are layer-wise equivalent to a shallow water system

insofar as variations in the vertical only appear implicitly in the elliptic nature of the

q-c relation. Although ageostrophic circulations do not explicitly occur in the

QGPV evolution equation, these circulations are vital to QG dynamics and may

be obtained diagnostically from the geostrophic mass ﬁeld and its time evolution

(Holton, 1992, Section 6.4).

This system is completed by the speciﬁcation of upper and lower boundary

conditions. The lower boundary condition over a rigid surface is

ð@

þ u

þ v

Þð@

c þ N

Þ¼0atz ¼ 0 ð7Þ

where h

(x, y) is the bottom topography. Recalling the connection between the

vertical derivative of the geostrophic stream function and the perturbation potential

temperature (3), condition (7) simply describes the material conservation of potential

temperature in the geostrophic wind at the lower boundary. If there is a rigid upper

boundary, another c ondition of the form (7) is applied there. In the atmosphere, this

condition is replaced by the requirement that either the perturbation energy density

decay as z !1, or alternatively, that the energy ﬂux be directed upward as z !1.

The robust extratropical zonally averaged ﬂow suggests studying small-amplitude

ﬂuctuations about that ﬂow. Dividing the stream function into a zonally symmetric

background and a perturbation,

cðx; y; z; tÞ¼c

ðy; zÞþc

ðx; y; z ; tÞð8Þ

*Forcing and dissipation are neglected not because they are unimportant to large-scale atmospheric

dynamical motions, but because their inclusion is not necessary to understand the dynamical features

examined herein. However, in general they will have important modifying effects in any given

circumstances and will be crucial in the study of any steady-state motions.

2 QUASI-GEOSTROPHIC THEORY 41

the evolution of the perturbation QGPV is described by

ð@

þ u

g 0

Þq

þ v

þ u

 Hq

¼ 0 ð9Þ

Here q

¼ @

þ @

þ r

1

ðr

Þ; u

¼ðu

; v

Þ¼ð@

Þ; u

g 0

@

; and

¼ b  @

 r

1

re@

g 0



ð10Þ

is the background QGPV gradient. The perturbation (rigid surface) boundary

condition is

ð@

þ u

Þð@

þ N

Þþv

þ u

 Hð @

Þ¼0atz ¼ 0 ð11Þ

where

1

½h

@

ð12Þ

is proportional to the basic state potential temperature gradient measured along the

sloping lower boundary, and the brackets indicate a zonal average.

We are free to seek wavelike solutions to Eqs. (8) and (9) of the form,

ðx; y; z ; tÞ¼Cðy; zÞe

ikðxctÞ

ð13Þ

where k is the (non-negative) wavenumber in the x (zonal) direction and c is the

complex phase speed, related to the frequency o ¼kc. Substituting in solutions of

this form and neglecting terms that are quadratic in perturbation quantities yields the

equation

ðu

 cÞ r

1

re@

þ @

 k



C þ q

C ¼ 0 ð14Þ

with the lower boundary condition

ðu

 cÞ@

C þ Z

C ¼ 0atz ¼ 0 ð15Þ

along with the appropriate upper boundary condition for the problem at hand. Jumps

in N or the shear, common at the tropo pause, may be included in (14) by applying

analytically derived jump conditions.

The linear, homogeneous system [Eqs. (14) and (15)] deﬁnes an eigenvalue

problem for c. A particularly illuminating case is where u

and N are constant,

r ¼r

exp(z=H), and the topography h

vanishes. In this situation, solutions to

(14) may be sought of the form

C ¼ A expðimzÞexp



expðilyÞð16Þ

42 EXTRATROPICAL ATMOSPHERIC CIRCULATIONS

where the complex constant A may be adjusted to meet the boundary condition (15).

For this particular solution, the zonal phase speed is given by

c ¼

¼ u



þ l

þ e ðm

ð17Þ

Waves of this type are called Rossby waves and provide an archetype for low-

frequency (o < f

) motions in the extratropics. Rossby waves differ from other,

more familiar wave types such as gravity waves, since it is the planetary vorticity

gradient b that acts as a restoring mechanism for the wave. An illuminating discus-

sion of the vorticity gradient as a restoring mechanism is found in Pedlosky (1987,

Section 3.16).

Rossby waves have a number of remarkable properties. First, the zonal phase

speed is everywhere westerly relative to the basic state zonal ﬂow u

.However,as

the total wavenumber K

¼k

þ l

þ e(m

þ 1=4H

) gets larger, Rossby waves

move more and more nearly with the basic ﬂow u

. These properties are entirely

consistent with observed large-scale atmospheric waves. Rossby waves are also

dispersive, i.e., the g roup velocity c

ð@o=@k;@o=@l;@o=@mÞ that describes how

a packet of Rossby waves moves with time differs from the phase velocity of the

waves comprising that packet in both magnitude and direction. Since information

travels with the group velocity, rather than the phase velocity, the group velocity also

describes the propagation of the energy of the packet. The difference between the

Rossby wave phase and group velocities is most apparent for vertical propagation,

since the vertical group velocity and phase velocity are oppositely directed. If the

lines of constant phase propagate upwards (downwards), the energy in the wave

propagates downwards (upwards).

While Rossby waves provide a nontrivial example of nearly geostrophic motions

in the extratropics, the actual extratropical ﬂow situation is signiﬁcantly more

complicated than that considered above. Speciﬁcally, vertical shear and associated

meridional temperature gradients allow for the existence of instabilities that can

amplify with time as well as propagate. The characteristics of such instabilities,

along with their importance in the extratropical atmospheric circulation form the

topic of the next section.

3 BAROCLINIC INSTABILITY AND FRONTOGENESIS

The most striking observational feature of the extratropical atmosphere is the spec-

trum of vigorous synoptic-scale transient eddies that provide much of the day-to-day

variability in the middle latitud e weather. These eddies arise from the release of

potential energy stored in the equator–pole temperature gradient. The release of this

potential temperature is marked by a down gradient ﬂux of heat from equator to

pole, leading to an equator–pole temperature gradient that is signiﬁcantly smaller

than radiative processes would provide acting alone. Curiously, this heat ﬂux can be

3 BAROCLINIC INSTABILITY AND FRONTOGENESIS 43

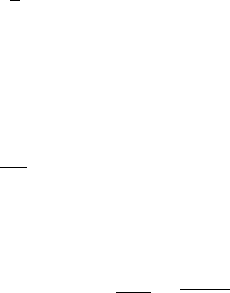
linked to the growth of transient eddies through the budget for the perturbation eddy

energy

ððð

r½u

þ v

þ e ð@

dx dy dz ð18Þ

The equation governing E

is obtained by multiplying (9) by c

, integrating over all

space, and employing the boundary condition (11). This equation can be written

ðð

Q  Hu

dy dz ð19Þ

where the Q vector is given by

Q ¼ðQ

; Q

Þðru

; rev

Þ; ð20Þ

and the overbar denotes an integral over x. It has been assum ed that the vertical ﬂux

terms vanish by a radiation condition as z !1, and the analogous lateral ﬂux terms

vanish by virtue of meridional conﬁnement in a channel, or equivalently, by decay of

perturbation s at large y.

The integral in (19) represents the conversion of energy between the background

ﬂow and perturbations. In the integrand, Q

g 0

is the baroclinic conversion term,

and represents energy exchange with the potential energy of the basic state. By

thermal wind balance, positive vertical shear implies colder air toward the pole;

and, in this situation, perturbations with a poleward heat ﬂux tap the baroclinic

energy and grow. This term releases potential energy by reducing the tilt of the

mean isentropes.

The term Q

is the barotropic conversion term and represents exchanges

with the basic state kinetic energy. In the extratropics, it typically acts as an energy

sink. Synoptic eddies thus act as an intermediary, transforming potential energy due

to differential heating into kinetic energy of barotropic jets.

For any basic state ﬂow with vertical or horizontal shear, an initial perturbation

can be crafted that will extract energy and begin to grow. However, as time passes,

the structure of the perturbation will generally change, and growth may cease or even

turn to decay. Stability theory seeks to identify energy-extracting structures that can

persist long enough to amplify by a signi ﬁcant amount and to understand what basic

state ﬂow circumstances allow for such growth. This is elegantly discussed with

reference to the wave action budget of the perturbation. If we linearize (9), multiply

by q

, and average over x, we obtain

A þ H  Q ¼ 0 ð21Þ

44 EXTRATROPICAL ATMOSPHERIC CIRCULATIONS

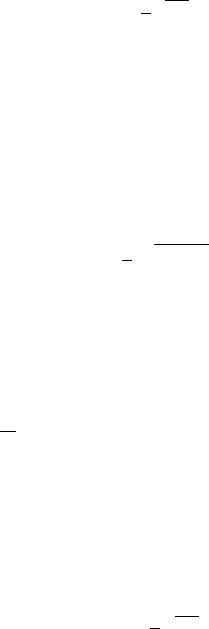
where the wave action (or more properly the pseudomomentum) A is

A ¼

1

ð22Þ

An analogous budget for the variance of temperature at the ground can be obtained

by multiplying (11) by r@

and averaging in x. Doing so yields

B þ Q

ð0Þ¼0atz ¼ 0 ð22Þ

where

B ¼

ð@

1

ð23Þ

Integrating (21) over space, assuming boundary conditions that make the horizontal

ﬂux terms vanish, and using (22) to reduce the bottom ﬂux contribution yields the

following relation for the total pseudomomentum

¼ 0

ðð

Adydzþ

Bdy ð24Þ

This conservation relation yields the desired stability criterion. Speciﬁcally, if q

and Z

each have uniform sign throughout the domain, have the same sign as each

other, and the magnitudes of q

and Z

are ﬁnite and bounded away from zero, then

the system is stable in the sense that the perturbation enstrophy

ðð

dy dz ð25Þ

remains small for all times if it is initially small. If this criterion is not met, sustained

exponential disturbance growth is possible. However, such growth is not inevitable,

as (24) provides a necessary rather than a sufﬁcient condition for disturbance

growth.

The archetypal scenario permitting baroclinic instability in the extratropics is q

greater than zero everywhere, positive vertical shear at the ground, and a sufﬁciently

ﬂat lower boundary to keep Z

negative. This condition is almost ubiquitously

satisﬁed throughout the extratropical troposphere in both hemispheres. In this situa-

tion, a growing disturbanc e can be regarded as a coupled QGPV=surface tempera-

ture motion. The QGPV anomaly aloft induces a motion that stirs up a surface

temperature anomaly, and the surface temperature anomaly in tur n further stirs up

the QGPV aloft. The inﬂuence depth of a QGPV or surface temperatu re perturbation

of length L is the ‘‘deformation depth’’ f

L=N provided this is not much in excess of

the density scale height H . If a QGPV anomaly is at altitud e D, motions with

3 BAROCLINIC INSTABILITY AND FRONTOGENESIS 45