Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

which may be inverted for the spherical coordinates:

l ¼ tan

1



f ¼ tan

1

þ x



r ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ x

ð23bÞ

Parcel displacements in the directions of increasing longitude, latitude, and radial

distance are then described by

dx ¼ r cos f dl

dy ¼ rdf

dz ¼ dr

ð24aÞ

in which vertical distance is measured by height

z ¼ r  a ð24bÞ

where a denotes the mean radius of Earth. Velocity components in the spheri cal

coordinate system are then expressed by

u ¼

¼ r cos f

v ¼

¼ r

w ¼

ð25Þ

The vector momentum equations may now be expressed in terms of the spherical

coordinates. Lagrangian derivatives of vector quantities are complicated by the

dependence on position of the coordinate vectors i, j, and k. Each rotates in physical

space under a displacement of longitude or latitude. For example, an air parcel

moving along a latitude circle at a constant speed u has a velocity v ¼u i, which

appears constant in the spherical coordinate representation, but which actually

rotates in physical space (Fig. 4). Consequently, the parcel experiences an accelera-

tion that must be accounted for in the equations of motion.

Consider the velocity

v ¼ ui þ vj þ wk

16 FUNDAMENTAL FORCES AND GOVERNING EQUATIONS

Since the spherical coordinate vectors i, j, and k are functions of position

xx,a

parcel’s acceleration is actually

i þ

j þ

k þ u

þ v

þ w



þu

þ v

þ w

ð26aÞ

where the subscript refers to the basic form of the Lagrangian derivative in Cartesian

geometry



þ v  H ð26bÞ

Cor rections appearing on the right-hand side of (26) can be evaluated by expressing

the spherical coordinate vectors in terms of the ﬁxed rectangular Car tesian coordi-

nate vectors e

, e

. Lagrangian derivatives of the spherical coordinate vectors then

follow as

¼ u

tan f

j 



¼u

tan f

i 

i þ

ð27Þ

With these, material accelerations in the spherical coordinate directions become





uv tan f

ð28aÞ



tan f

ð28bÞ





þ v



ð28cÞ

3 MOMENTUM BUDGET 17

Introducing (28), making use of the atmosphere’s shallowness (z a), and

formally adopting height as the vertical coordinate then casts the momentum equa-

tions into component form:

 2Oð v sin f  w cos fÞ¼

ra cos f

þ uv

tan f



 D

ð29aÞ

þ 2Ou sin f ¼



tan f



 D

ð29bÞ

 2Ou cos f ¼

 g þ

þ v

 D

ð29cÞ

4 FIRST LAW OF THERMODYNAMICS

For the material volume V ðtÞ, the ﬁrst law of thermodynamics is expressed by

V ðtÞ

TdV

¼

SðtÞ

q  n dS



V ðtÞ

qqdV

ð30Þ

where c

is the speciﬁc heat at constant volume, so c

T represents the internal energy

per unit mass, q is the local heat ﬂux so q n represents the heat ﬂux ‘‘into’’ the

material volume, a ¼ 1=r is the speciﬁc volume so pda=dt represents the speciﬁc

work rate, and

qq denotes the speciﬁc rate of internal heating (e.g., associated with the

latent heat release and frictional dissipation of motion).

In terms of speciﬁc volume, the continuity equation (6) becomes

¼ H  v ð31Þ

Incorporating (31), along with Reynolds’ transport theorem (3) and Gauss’ theorem,

transforms (30) into

V ðtÞ

þ H  q þ pH  v  r



¼ 0

Since V(t) is arbitrary, the quantity in brackets must again vanish identically. There-

fore, the ﬁrst law applied to individual bodies of air requires

¼H  q  p H  v þ r

qq ð32Þ

to be satisﬁed continuously.

18 FUNDAMENTAL FORCES AND GOVERNING EQUATIONS

The heat ﬂux can be separated into radiative and diffusive components:

q ¼ q

þ q

¼ F  kHT

ð33Þ

where F is the net radiative ﬂux and k is the thermal conductivity in Fourier’s law of

heat conduction. The ﬁrst law then becomes

þ pH  v ¼H F þ H ðkHT Þþr

qq ð 34Þ

Known as the thermodynamic equation, (34) expresses the rate that a material

element’s internal energy changes in terms of the rate that it performs work and

the rate that it absorbs heat through convergence of radiative and diffusive energy

ﬂuxes.

The ther modynamic equation is expressed more compactly in terms of another

thermodynamic property, one that account s collectively for a change of internal

energy and expansion work. The potential temperature y is deﬁned as



ð35Þ

where k ¼ R=c

; R is the speciﬁc gas constant for air, and temperature and pressure

are related through the ideal gas law

p ¼ rRT ð36Þ

and y is related to a parcel’s entropy. It is conserved during an adiabatic process, as

characterizes a parcel ’s motion away from Earth’s surface and cloud. Incor porating y

into the second law of thermodynamics (e.g., Salby, 1996) then leads to the funda-

mental relation

d ln y

þ p

ð37Þ

where d=dt represents the Lagrangian derivative. Making use of the continuity

equation (31) transforms this into

¼ rc

þ pH  v ð38Þ

4 FIRST LAW OF THERMODYNAMICS 19

Then incorporating (38) into (34) absorbs the expansion work into the time rate of

change of y to yield the thermodynamic equation

¼H  F þ H ðkHT Þþr

qq ð39Þ

Equation (39) relates the change in a parcel’s potential temperature to net heat

transfer with its surroundings. In the absence of such heat transfer, y is conserved

for individual air parcels.

REFERENCES

Aris, R. (1962). Vectors, Tensors, and the Basic Equations of Fluid Mechanics, Englewood

Cliffs, NJ, Prentice Hall.

Iribarne, J., and W. Godson (1981). Atmospheric Thermodynamics, Reidel, Dordrecht.

Salby, M. (1996). Fundamentals of Atmospheric Physics, San Diego, Academic.

FUNDAMENTAL FORCES AND GOVERNING EQUATIONS

CHAPTER 3

CIRCULATION, VORTICITY, AND

POTENTIAL VORTICITY

PAUL J. KUSHNER

1 INTRODUCTION

Vorticity and circulation a re closely related quantities that describe rotat ional motion

in ﬂuids. Vorticity describes the rotation at each point; circulation describes rotation

over a region. Both quantities are of fundamental importance to the ﬁeld of ﬂuid

dynamics. The distribution and statistical properties of the vorticity ﬁeld provide a

succinct characterization of ﬂuid ﬂow, particularly for weakly compressible or

incompressible ﬂuids. In addition, stresses acting on the ﬂuid are often interpreted

in terms of the generation, transport, and dissipation of vorticity and the resulting

impact on the circulation.

Potential vorticity (PV) is a generalized vorticity that combines information about

both rotational motion and density stratiﬁcation. PV is of central importance to the

ﬁeld of geophysical ﬂuid dynamics (GFD) and its subﬁelds of dynamical meteor-

ology and physical oceanography. Work in GFD often focuses on ﬂows that are

strongly inﬂuenced by planetary rotation and stratiﬁcation. Such ﬂows can often be

fully described by their distribution of PV. Similarly to vorticity, the generation,

transport, an d dissipation of PV is closely associated with stresses on the ﬂuid.

Vorticity, circulation, and PV are described extensively in several textbooks (e.g.,

Holton, 1992; Gill, 1982; Kundu, 1990; Salmon, 1998). This review is a tutorial,

with illustrative examples, that is meant to acquaint the lay reader with these

concepts and the scope of their application. An appendix provides a mathematical

summary.

Handbook of Weather, Climate, and Water: Dynamics, Climate, Physical Meteorology, Weather Systems,

and Measurements, Edited by Thomas D. Potter and Bradley R. Colman.

ISBN 0-471-21490-6 # 2003 John Wiley & Sons, Inc.

2 CIRCULATION AND VORTICITY: DEFINITIONS AND EXAMPLES

Circulation is a physical quantity that describes the net movement of ﬂuid along a

chosen circuit, that is, a path, taken in a speciﬁed direction, that starts at some point

and returns to that point.

Statement 1. The circulation at a given time is the average, over a circuit, of the

component of the ﬂow velocity tangential to the circuit, multiplied by the length of the

circuit. Circulation therefore has dimensions of length squared per unit time.

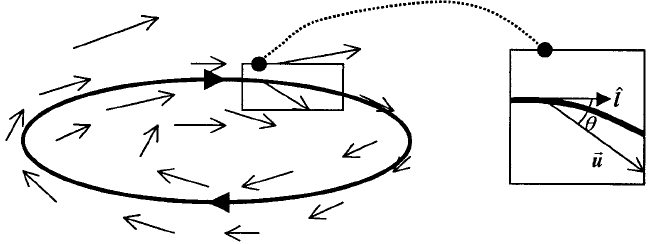
Consider the circuit drawn as a heavy curve in Figure 1 for a ﬂuid whose velocity

u is indicated by the arrows. At each point we may split the velocity into components

tangential to and perpendicular to the local direction o f the circuit. The tangential

component is deﬁned as the dot product u 

ll ¼jujcos y, where

ll is a unit vector that

points in the direction tangential to the circuit and y is the angle between u and

ll.

Note that

ll points in the speciﬁed direction chosen for the circuit. Where y is acute,

the tangential compo nent is positive, where oblique, negative, and where a right

angle, zero. To calculate the circulation, we average over ‘‘all’’ point s along the

circuit. (Although we cannot actually average over all points along the circuit, we

can approximate such an average by summing over the tangential component

u 

ll ¼jujcos y at evenly and closely spaced points around the circuit and by divid-

ing by the number of points.) The circulation would then be this average, multiplied

by the length of the circuit. (In the Appendix, the circulation is deﬁned in terms of a

line integral.)

The circulation is not deﬁned with reference to a particular point in space but to a

circuit that must be chosen. For example, to measure the strength of the primary

near-surface ﬂow around a hurricane in the Northern Hemisphere, a natural circuit is

a circle, oriented horizontally, centered about the hur ricane’s eye, of radius somewhat

larger than the eye, and directed counterclockwise when viewed from above. We thus

have speciﬁed that the circuit r un in the ‘‘cyclonic’’ direction, which is the direction

of the primary ﬂow around tropical storms and other circulations with low-pressure

centers in the Nor thern Hemisphere (Fig. 2).

Figure 1 Heavy curve, dark arrows: circuit. Light arrows: ﬂow velocity.

CIRCULATION, VORTICITY, AND POTENTIAL VORTICITY

Suppose that the average ﬂow tangential to the circuit is approximately

u ¼40 m=s and that the radius of the circle is r ¼100 km. The circulation, G,

using the deﬁnition above, is then the average tangential ﬂow times the circumfer-

ence of the circle: G ¼2pru 2.5 10

=s. If the circu it were chosen to run

clockwise, i.e., opposite to the primary ﬂow, instead of counte rclockwise, the circu-

lation would be of the same strength but of opposite sign.

Circulation is a selective measure of the strength of the ﬂow: It tells us nothing

about components of motion perpendicular to the circuit or components of the ﬂow

that average to zero around the circuit. For example, suppose the hurricane is blown

to the west with a constant easterly wind. This constant wind will not contribute to

the circulation: Since cosðy þ pÞ¼cos y, every point on the north side of the

circle that contributes some amount to the circulation has a counterpart on the south

side that contributes an equal and opposite amount. As another example, the circuit

in Figure 2 would not measure the strength of the hurricane’s secondary ﬂow, which

runs toward the eye near the surface and away from the eye aloft (dotted arrows

in Fig. 2). The reader might try to imagine a circuit that would measure this secon-

dary ﬂow.

The hurricane example might suggest that the ﬂuid must ﬂow around the chosen

circuit for the circulation to be nonzero; however, this need not be true. For example,

consider the circuit shown in Figure 3, which shows a vertically oriented 50- 200-

m rectangular circuit in a west-to-east ﬂow whose strength increases linearly with

height, according to the formula u(z) ¼az, where z is the height in meters and

a ¼0.01=s ¼(10 m=s) km is the ‘‘vertical shear,’’ that is, the rate of change of the

wind with respect to height. This is a value of vertical shear that might be encoun-

tered in the atmospheric boundary layer. If the direc tion of the circuit is chosen, as in

the ﬁgure, to be clockwise, the circulation in this example is the average of the

along-circuit component of the ﬂow weighted by the length of each side,

50  uðtopÞ50  uðbottomÞþ200  0 þ 200  0

50 þ50 þ 200 þ 200

50  200a

500

¼ 0:2m=s

times the perimeter of the rectangle, giving G ¼100 m

=s. Note that the vertical sides

make no contribution to the circulation since the ﬂow is perpendicular to them.

Figure 2 Circuit shown with bold curve. symbol represents a paddle wheel with its axis in

the vertical and located at the center of the circle.

2 CIRCULATION AND VORTI CITY: DEFINI TIONS AND EXAMPLES 23

Thus, shear alone can make the circulation nonzero even though the ﬂow is not

actually moving around the circuit.

What, then, does the circulation represent in these examples, if not the strength of

the ﬂow around the circuit? In general, circulation represents the ability of a given

ﬂow to rotate mass elements in the ﬂuid and objects placed in the ﬂow. Imagine a

paddle wheel placed within the circuits in Figures 2 and 3 [see, e.g., Holton (1992),

Fig. 4.6], with axis perpendicular to the plane of the circuit. In the hurricane illus-

tration, the paddle wheel rotates counterclockwise; in the vertical shear-ﬂow, clock-

wise. In both examples, when the paddle wheel turns in the same direction as the

circuit in the illustration, the sign of the circulation is positive.

Circulation depends on many details about the circuit: its size, shape, orientation,

direction, and location. For example, in Figure 3, we could make the circulation

arbitrarily large by increasing the length of the sides of the circuit. It is useful to

deﬁne a quantity that measures rotation but that does not refer to the details of any

particular circuit. It is also useful to deﬁne a ‘‘microsc opic’’ quantity that measures

rotation at individual points instead of a ‘‘macroscopic’’ quantity that measures

rotation over a region. This leads us to vorticity.

Statement 2. The vorticity in the right-hand-oriented direction perpendicular to the

plane of a circuit is equal to the circulation per unit area of the circuit in the small-area

limit. Vorticity is, therefore, a quantity with dimensions of inverse time. In order to

deﬁne the x, y, and z components of the vorticity, we consider circuits whose

perpendicular lies in each of these directions.

Statement 2 requires some explanation. Consider the circulation for a circuit

which, for simplicity, we assume to be ﬂat. This deﬁnes a unique direction that is

perpendicular to the plane of the circuit if we use the ‘‘right-hand rule.’’ This rule

works as follows: Curl the ﬁngers of the right hand in the direction of the circuit,

Figure 3 Circuit shown with bold line. symbol represents paddle wheel with rotation axis

coming out of page.

CIRCULATION, VORTICITY, AND POTENTIAL VORTICITY

e.g., clockwise in Figure 3. Then point the right-hand thumb in a direction perpen-

dicular to the circuit: into the page in Figure 3. In statement 2, we refer to this

direction as the ‘‘right-hand-oriented direction normal to the plane of the circuit.’’

Now, imagine reducing the size of the circuit until it becomes vanishingly small. In

Figure 3, for example, we could imagine reducing the loop to 5 20 m, then

5 20 mm, and so on. In statement 2, we refer to this as the ‘‘small-area limit.’’

Therefore, vorticity describes rotation as a microscopic quantity.

We can calculate vorticity in the previous examples. For the shear-ﬂow example

(Fig. 3), it is easy to show that the circulation around the loop is aA, where A is the

area of the rectangular loop. With more effort, it can be shown that the circulation is

aA for any loop if A is taken to be the cross-sectional area of the loop in the plane of

the ﬂow. Therefore, the vorticity in the plane of the ﬂow is into the page and equal to

a ¼0.01=s everywhere. The reader should try to verify that the other two compo-

nents of the vorticity are zero because the associated circulation is zero. In hurri-

canes, as is typical of other vortices, the vorticity varies strongly as a function of

distance from the eye. The average vertical component of vorticity in our example is

upward and equal to the circulation divided by the total area of the circle:

G=A ¼2pru=(pr

) ¼2u=r 10

3

=s.

In GFD, there are three types of vorticity: absolute, planetary, and relative. The

absolute vorticity is the vorticity measured from an inertial frame of reference,

typically thought of as outer space. The planetary vorticity is the vorticity associated

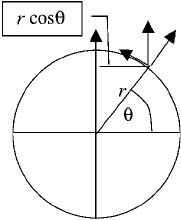
with planetary rotation. Earth rotates with a period of T 24 h from west to east

around the north pole–south pole rotation axis (Fig. 4). Consider a ﬂuid with zero

ground speed, meaning that it is at rest when measured from the frame of reference

of Earth. This ﬂuid will also be rotating with period T from west to east. The ﬂuid is

said to be ‘‘in solid-body rotat ion’’ because all the ﬂuid elements maintain the same

distance from one another over time, just as the mass elements do in a rotating solid.

The distance from the axis of rotation is r cos y, the component of the velocity

tangential to this rotation is 2pr cos y=T, the circumference of the latitude circle

is 2pr cos y, and the circulation, by statement 1, is the product of the two last

Figure 4 Geometry of Earth. Latitude is y The vertical vector is the vorticity of solid-body

rotation. The distance from the surface to the axis of rotation is r cos y. The component of the

planetary vorticity perpendicular to the surface is 4p sin y=T. The component tangential to the

surface is 4p cos y=T.

2 CIRCULATION AND VORTI CITY: DEFINI TIONS AND EXAMPLES 25