Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

be viewed more as a sampler than an exhaustive treatise on the dynamics of atmo-

spheric motions. For those intrigued by works presented here and wishing to further

learn about the area, the following texts are recommend ed in addition to those texts

and publications cited by the individual authors: An Introduction to Dynamical

Meteorology (1992) by J. R. Holton, Academic Press; Atmosphere-Ocean Dynamics

(1982) by A. E. Gill, Academic Press; and Geophysical Fluid Dynamics (1979) by

J. Pedlosky, Springer.

REFERENCES

Bjerknes, V. (1904). Das problem von der wettervorhersage, betrachtet vom standpunkt der

mechanik un der physik, Meteor. Z. 21, 1–7.

Charney, J. G. (1948). On the Scale of Atmospheric Motions, Geofys. Publik. 17, 1–17.

Hadley, G. (1735). Concerning the cause of the general trade-winds, Phil. Trans. 29, 58–62.

Lorenz, E. N. (1963). Deterministic Nonperiodic Flow, J. Atmos. Sci. 20, 130–141.

Lorenz, E. N. (1967). The Nature and Theory of the General Circulation of the Atmosphere,

World Meteorological Organization=Geneva.

Phillips, N. A. (1963). Geostrophic motion, Rev. Geophys. 1, 123–176.

Thompson, P. D. (1957). Uncertainty of the initial state as a factor in the predictability of large

scale atmospheric ﬂow patterns, Tellus 9, 257–272.

von Helmholtz, H. (1888). On Atmospheric motions, Sitz.-Ber. Akad. Wiss. Berlin 647–663.

OVERVIEW—ATMOSPHERIC DYNAMICS

CHAPTER 2

FUNDAMENTAL FORCES AND

GOVERNING EQUATIONS

MURRY SALBY

1 DESCRIPTION OF ATMOSPHERIC BEHAVIOR

The atmosphere is a ﬂuid and therefore capable of redistributing mass and consti-

tuents into a variety of complex conﬁgurations. Like any ﬂuid system, the atmo-

sphere is governed by the laws of continuum mechanics. These can be derived from

the laws of mechanics and thermodynamics governing a discrete ﬂuid body by

generalizing those laws to a continuum of such systems. The discrete system to

which these laws apply is an inﬁnitesimal ﬂu id element or air parcel, deﬁned by a

ﬁxed collection of matter.

Two frameworks are used to describe atmospheric behavior. The Eulerian

description represents atmospheric behavior in terms of ﬁeld properties, such as

the instantaneous distributions of temperature and motion. It lends itself to numerical

solution, forming the basis for most numerical models. The Lagrangian description

represents atmospheric behavior in terms of the properties of individual air parcels,

the positions of which must then be tracked. Despite this complication, the laws

governing atmospheric behavior follow naturally from the Lagrangian description

because it is related directly to transformations of properties within an air parcel and

to interactions with its environment.

The Eulerian and Lagrangian descriptions are related through a kinematic

constraint: The ﬁeld property at a given position and time must equal the property

possessed by the air parcel occupying that position at that instant. Consider the pro-

perty c of an individual air parcel, which has instantaneous position (x, y, z, t) ¼

Handbook of Weather, Climate, and Water: Dynamics, Climate, Physical Meteorology, Weather Systems,

and Measurements, Edited by Thomas D. Potter and Bradley R. Colman.

ISBN 0-471-21490-6 # 2003 John Wiley & Sons, Inc.

(x, t). The incremental change of c(x, t) during the parcel’s displacement

(dx, dy, dz) ¼dx follows from the total differential:

dc ¼

dt þ

dx þ

dy þ

dt þ Hc  dx

ð1Þ

The property’s rate of change following the parcel is then

þ u

þ v

þ w

þ v  Hc

ð2Þ

where v ¼dx=dt is the three-dimensional velocity. Equation (2) deﬁnes the Lag-

rangian derivative of the ﬁeld variable c(x , t), which corresponds to its rate of

change following an air parcel. The Lagrangian derivative contains two contr ibu-

tions: @ c=@ t represents the rate of change introduced by transience of the ﬁe ld

property c, and v Hc represents the rate of change introduced by the parcel’s

motion to positions of different ﬁeld values.

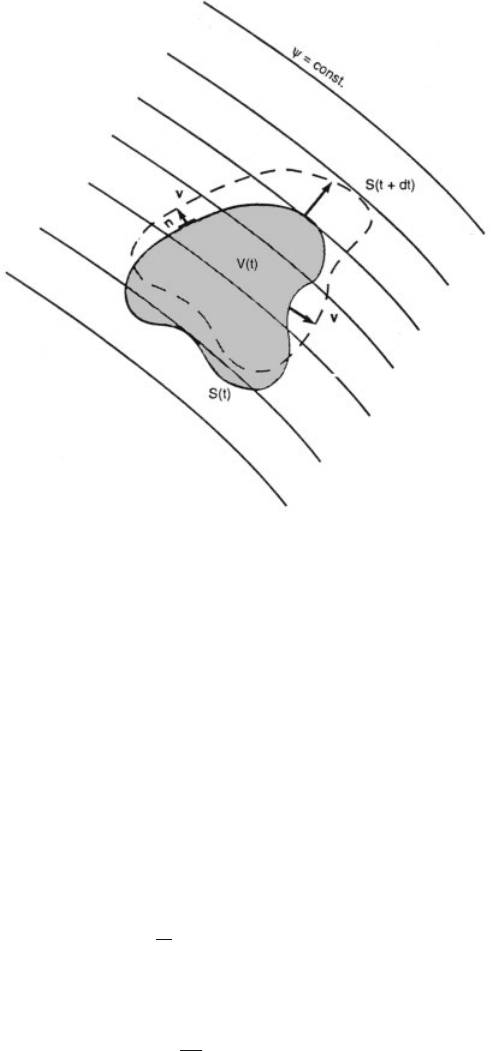
Consider now a ﬁnite body of air having instantaneous volume V(t). The integral

property

V ðtÞ

cðx; y; z; tÞdV

changes through two mechanisms (Fig. 1), analogous to the two contributions to

dc=dt: (1) Values of c(x, t) within the material volume change du e to unsteadiness

of the ﬁeld. (2) The material volume moves to regions of different ﬁeld values.

Relative to a frame moving with V(t), this motion introduces a ﬂux of property c

across the material volume’s surface S(t). Collecting these contributions and apply-

ing Gauss’ theorem [see, e.g., Salby (1996)] leads to the identity

V ðtÞ

c dV

V ðtÞ

þ H ðvcÞ



V ðtÞ

þ cH  v



ð3Þ

Known as Reynolds’ transport theorem, (3) constitutes a transformation between the

Lagrangian and Eulerian descriptions of ﬂuid motion, relating the time rate of

change of some property of a ﬁnite body of air to the corresponding ﬁeld variable

and the motion ﬁeld v(x, t). Applying Reynolds’ theorem to particular properties

8 FUNDAMENTAL FORCES AND GOVERNING EQUATIONS

then yields the ﬁeld equations governing atmospheric behavior, which are known

collectively as the equations of motion.

2 MASS CONTINUITY

A material volume V(t) has mass

V ðtÞ

rðx; tÞdV

where r is density. Since V( t) is compr ised of a ﬁxed collection of matter, the time

rate of change of its mass must vanish

V ðtÞ

rðx; tÞdV

¼ 0 ð4Þ

Applying Reynolds’ theorem transforms (4) into

V ðtÞ

þ rH  v



¼ 0 ð5Þ

Figure 1 Finite material volume V(t), containing a ﬁxed collection of matter, that is

displaced across a ﬁeld property c. (Reproduced from Salby, 1996.)

2 MASS CONTINUITY 9

where the Lagrangian derivative is given by (2). This relation must hold for ‘‘arbi-

trary’’ material volume V(t). Consequently, the quantity in brackets must vanish

identically. Conservation of mass for individual bodies of air therefore requires

þ rH  v ¼ 0 ð6Þ

which is known as the continuity equation.

Budget of Constituents

For a speciﬁc property f (i.e., one referenced to a unit mass), Reynolds’ transport

theorem simpliﬁes. With (6), (3) reduces to

V ðtÞ

rfdV

V ðtÞ

ð7Þ

where rf represents the concentration of property f (i.e., referenced to a unit

volume).

Consider now a constituent of air, such as water vapor in the troposphere or ozone

in the stratosphere. The speciﬁc abundance of this species is described by the mixing

ratio r, which measures its local mass referenced to a unit mass of dry air (i.e., of

ﬁxed composition) . The corresponding concentration is then rr.

Conservation of the species is then expressed by

V ðtÞ

rrdV

V ðtÞ

PPdV

ð8Þ

which equates the rate that the species changes within the material volume to its net

rate of production per unit mass

PP, collected over the material volume. Applying (7)

and requiring the result to be satisﬁed for arbitrary V(t) then reduces the constituent’s

budget to

PP ð9Þ

Like the equation of mass continuity, (9) is a partial differential equation that must

be satisﬁed continuously throughout the atmosphere. For a long-lived chemical

species or for water vapor away from regions of condensation,

PP ﬃ 0, so r is

approximately conserved for individual air parcels. Otherwise, production and

destruction of the species are balanced by changes in a parcel’s mixing ratio.

10 FUNDAMENTAL FORCES AND GOVERNING EQUATIONS

3 MOMENTUM BUDGET

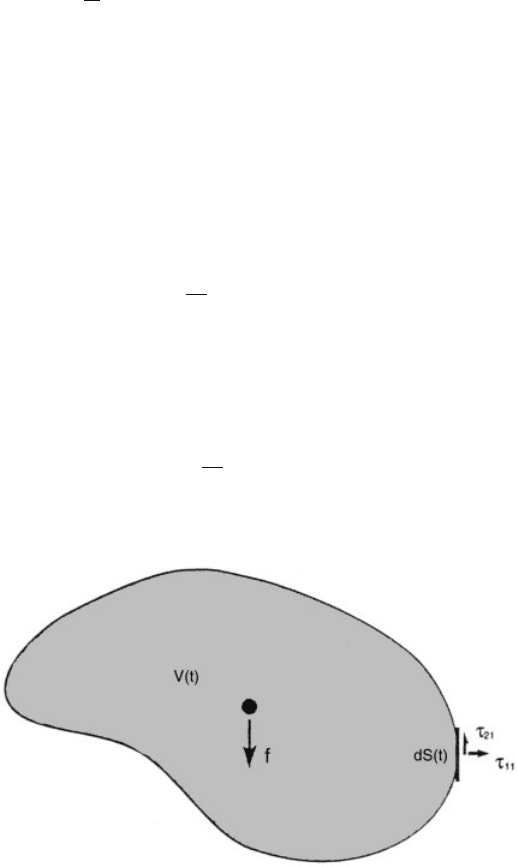
In an inertial reference frame, Newton’s second law of motion applied to the material

volume V(t) may be expressed

V ðtÞ

rv dV

V ðtÞ

rf dV

SðtÞ

t  n dS

ð10Þ

where rv is the concentration of momentum, f is the body force per unit mass acting

internal to the material volume, and t is the stress tensor acting on its surface

(Fig. 2). The stress tensor t represents the vector force per unit area exerted on

surfaces normal to the three coordinate directions. Then t  n is the vector force per

unit area exerted on the section of material surface with unit normal n, representing

the ﬂux of vector momentum across that surface.

Incorporating Reynolds’ theorem for a concentration (7), along with Gauss’

theorem, casts the material volume’s momentum budget into

V ðtÞ

 rf  H  t



¼ 0 ð11Þ

As before, (11) must hold for arbitrary material volume, so the quantity in brackets

must vanish identically. Newton’s second law for individual bodies of air thus

requires

¼ rf þ H  t ð12Þ

to be satisﬁed continuously.

Figure 2 Finite material volume V(t) that experiences a speciﬁc body force f internally and a

stress tensor t on its surface. (Reproduced from Salby, 1996.)

3 MOMENTUM BUDGET 11

The body force relevant to the atmosphere is gravity

f ¼ g ð13Þ

which is speciﬁed. The stress term, on the other hand, is determined autonomously

by the mot ion. It represents the divergence of a momentum ﬂux, or force per unit

volume, and has two components: (i) a normal force associated with the pressure

gradient Hp and (ii) a tangential force or drag D introduced by friction. For a

Newtonian ﬂuid such as air, tangential components of the stress tensor depend

linearly on the shear. Frictional drag then reduces to (e.g., Aris, 1962)

D ¼

H  t

¼

H ðmHvÞð14Þ

where m is the coefﬁcient of viscosity. The right-hand side of (14) accounts

for diffusion of momentum, which is dominated in the atmosphere by turbulent

diffusion (e.g., turbulent mixing of an air parcel’s momentum wi th that of its

surroundings). For many applications, frictional drag is expressed in terms of a

turbulent diffusivity n as

D ¼n

ð15Þ

in which horizontal components of v and their vertical shear prevail.

With these restrictions, the momentum budget reduces to

¼ g 

Hp  D ð16Þ

which comprise the so-called Navier–Stokes equations. Also called the momentum

equations, (16) assert that an air parcel’s momentum changes according to the

resultant force exerted on it by gravity, pressure gradient, and frictional drag.

Momentum Budget in a Rotating Reference Frame

The momentum equations are a statement of Newton’s second law, so they are valid

in an inertial reference frame. The reference frame of Earth, on the other hand, is

rotating and consequently noninertial. The momentum equations must therefore be

modiﬁed to account for acceleration of the frame in which atmospheric motion is

observed.

Consider a reference frame that rotates with angular velocity V. A vector A that

appears constant in the rotating frame rotates when viewed from an inertial frame.

12 FUNDAMENTAL FORCES AND GOVERNING EQUATIONS

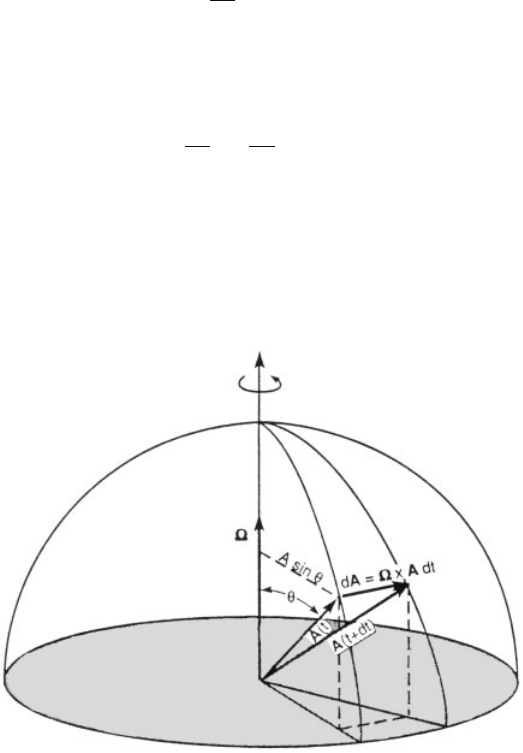
During an interval dt, A changes by a vector increment dA that is perpendicular to

the plane of A and V (Fig. 3) and has magnitude

jdAj¼A sin y  O dt

where y is the angle between A and V. The time rate of change of A apparent in an

inertial frame is then described by



¼ V  A ð17Þ

More generally, a vector A that has the time rate of change dA=dt in the rotating

reference frame has the time rate of change



þ V  A ð18Þ

in an inertial reference frame.

Consider now the position x of an air parcel. The parcel’s velocity v ¼dx=dt

apparent in an inertial reference frame is then

¼ v þ V  x ð19Þ

Figure 3 A vector A ﬁxed in a rotating reference frame changes in an inertial reference

frame during an interval dt by the increment jdAj¼A sin y  O dt in a direction orthogonal to

the plane of A and O, or by the vector increment dA ¼ V  A dt. (Reproduced from Salby,

1996.)

3 MOMENTUM BUDGET 13

Likewise, the acc eleration apparent in the inertial frame is given by



þ V  v

which upon consolidation yields for the acceleration apparent in the inertial frame:



þ 2V  v þ V ðV  xÞð20Þ

Earth’s rotation introduces two corrections to the parcel’s acceleration: (i) 2V  v

is the Coriolis acceleration. It acts perpendicular to the parcel’s motion and the

planetary vorticity 2V. (ii) V ðV  xÞ is the centrifugal acceleration of the air

parcel associated with Earth’s rotation. When geopotential coordinates are used (e.g.,

Iribarne and Godson, 1981), this correction is absorbed into the effective gravity:

g ¼HF, which is deﬁned from the geopotential F.

Incorporating (20) transforms the momentum equations into a form valid in the

rotating frame of Earth:

þ 2V  v ¼

Hp gk  D ð21Þ

where g is understood to denote effective gravity and k the upward normal in the

direction of increasing geopotential. The correction 2V v is important for motions

with time scales comparable to that of Earth’s rotation. When moved to the right-

hand side, it enters as the Coriolis force: 2V  v, a ﬁctitious force that acts on an

air parcel in the rotating frame of Earth. Because it acts orthogonal to the parcel’s

displacement, the Coriolis force performs no work.

Component Equations in Spherical Coordinates

In vector form, the momentum equations are valid in any coordinate system.

However, those equations do not lend themselves to standard methods of solution.

To be useful, they must be cast into component form, which then depend on the

coordinate system in which they are expressed.

Consider the recta ngular Cartesian coordinates x ¼ðx

; x

Þ having origin at

the center of Earth (Fig. 4) and the spherical coordinates

x ¼ðl; f; rÞ

14 FUNDAMENTAL FORCES AND GOVERNING EQUATIONS

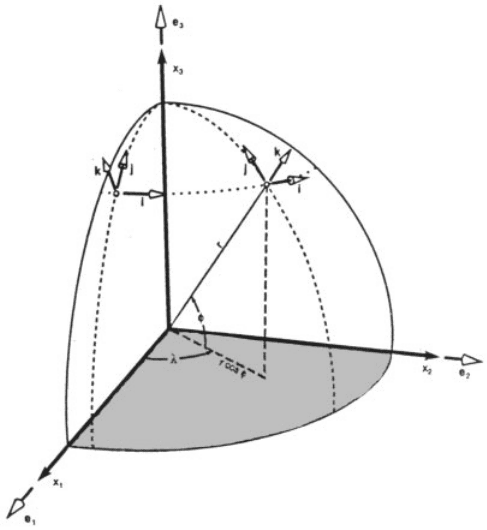
both ﬁxed with respect to Earth. The corresponding unit vectors

¼ i

¼ j

¼ k

ð22Þ

point in the directions of increasing l; f, and r and are mutually perpendicular.

The rectangular Cartesian coordinates can be expressed in terms of the spherical

coordinates as

¼ r cos f cos l

¼ r cos f sin l

¼ r sin f

ð23aÞ

Figure 4 Spherical coordinates: longitude l, latitude f, and radial distance r. Coordinate

vectors e

¼i, e

¼j, and e

¼k change with position (e.g., relative to ﬁxed coordinate vectors

, e

, and e

of rectangular Cartesian coordinates). (Reproduced from Salby, 1996.)

3 MOMENTUM BUDGET 15