Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

Relative Humidity

We deﬁne relative humidity to be the ratio of the vapor pressure to the vapor pressure

exerted by a plain surface of pure water. There is a relative humidity for liquid (H

)

and a relative humidity over ice (H

which is approximately equal to



ð56Þ



ð57Þ

where r

and r

are the saturation mixing ratios over liquid and ice.

8 TEMPERATURE VARIABLES

Virtual Temperature (T

)

We now apply the ideal gas law to the mixture of air and vapor. Applying the total

pressure is given by Dalton’s law, p ¼ p

þ e

, to the equation of state separately to

the vapor and dry air components, we obtain the modiﬁed equation of state:

p ¼ rR

1 þ



1 þ r

¼ rR

ð58Þ

where T

 Tð1:0 þ 0:61r

Þ is the virtual temperature. Note the effect of adding

moisture is to increase the virtual temperature over the temperature. Since the total

density is a function of the pressure and virtual temperature, the addition of moisture

actually lowers the air density. This tends to be opposite to the common perception

that humid air is ‘‘heavy.’’

Dew Point Temperature (T

)

This is the temperature to which moist air must be cooled at constant pressure and

vapor mixing ratio in order to become saturated over a plane surface of pure water.

226 MOIST THERMODYNAMICS

Dew point temperat ure can be calculated with the following algorithm:

35:86 ln e

 4947:2325

ln e

 23:6837

ð59Þ

where e

is in millibars and T

is in Celsius.

Wet-Bulb Temperature (T

)

The wet bulb temperature is the temperature that a ventillated thermometer wrapped

in a wet cloth will have due to evaporation from the cloth. This will be colder than

the air temperature.

The wet-bulb temperature (T

) may be deﬁned by the isobaric or the adiabatic

process.

Isobaric Process T

is the temperature to which air will cool by evaporating

water into it at constant pressure until it is saturated. The latent heat is assumed to be

supplied by the air. Note that r

is not kept constant and so T

differs from T

When measured by a psychrometer, the air is caused to move rapidly past two

thermometer bulbs, one dry and the other shrouded by a water-soaked cloth. When

thermal equilibrium is reached on the wet bulb, the loss of heat by air ﬂowing past

the wet bulb must equal the sensible heat, which is transformed to latent heat. Hence,

ðT  T

Þðc

þ r

Þ½r

ðT

; pÞr

l

; ð 60 Þ

where T is the temperature of the air approaching the wet bulb.

Given temperature and mixing ratio, and a suitable relation for obtaining r

ðT

and l

, one can solve for T

. Alternatively, one can measure T and T

directly with a

psychrometer, and knowing pressure solve for r

Adiabatic Process One can ﬁnd T

graphically with the aid of a thermody-

namic diagram using the following steps:

1. Begin with pressure an d mixing ratio.

2. Reduce pressure dry-adiabatically until saturation is reached to ﬁnd tempera-

ture and pressure of lifting condensation level (LCL).

3. Increase pressure moist-adiabatically from LCL to original pressure.

4. The temperature at the original pressure is T

This is sometimes called the wet-adiabatic wet-bulb temperature. It differs at most a

few tenths of a degree from the other wet-bulb temperature.

8 TEMPERATURE VARIABLES 227

9 ENTROPY VARIAB LES FOR MOIST AIR

Potential Temperature for Moist Air (

)

We earlier derived the Poisson’s equation for y relative to a dry air parcel. Later we

pointed out that the conservation of y in a dry parcel, was equivalent to the conser-

vation of entropy for a dry adiabatic, reversible process. Hence, we could show that

d ln y ¼ ds: ð61Þ

We now extend our deﬁ nition of y to a system containing vapor gas as well as dry

air. To derive this, we return to Eq. (52) and assume an adiabatic reversible system

with no condensation or sublimation. We then can deﬁne y

for an adiabatic process:

d ln y

¼ dðc

ln TÞdðR

ln pÞ¼

: ð62Þ

Assuming that c

and R

are constant for an adiabatic process, we now deﬁne y

 T



: ð 63Þ

Now, Eq. (63) can be written as:

ð64Þ

The term y

differs only about 1% from the y deﬁned earlier. As a result, distinction

between y and y

is usually neglected in meteorological applications and the simpler

y is used as the standard form or potential temperature.

The term y, unlike T, takes into account the natural cooling of air as it rises from

pressure change so that one can compare air parcels at different elevations to deter-

mine which parcel is warmer or colder when brought to a common elevation. Our

intuitive concepts such as ‘‘cold air sinks’’ or ‘‘warm air rises’’do not work over deep

atmospheric depths because of this. Hence it nor mally gets colder with height, but

the low-level air does not start to rise. Our intuitive concepts do work, however,

when we use y as our temperature variable. If warmer y occurs below colder y air,

the underlying warm air will, in fact, rise spontaneously. Features such as a cold air

mass do appear as cold dense ﬂowing masses when viewed with y instead of

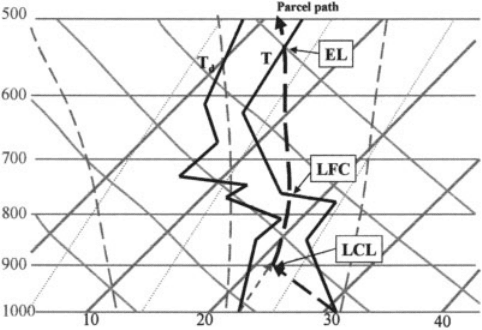
temperature. Figure 6 depicts a frontal system ﬂowing southward over the central

United States. Note that the cold air dams up against the Rockies to the west. One

can see the wavelike feature on the eastern side of the cold air mass representing

warm front and cold frontal features.

Using y in atmospheric science naturally makes the air conceptually easier to

understand as a ﬂuid. It also makes formulations depicting the dynamics and evolu-

tion of the ﬂow easier and more straightforward. Since air will tend to conser ve its

potential temperature unless diabatic effects are occurring, air naturally tends to

move along y surfaces. As a consequence, there is a better relationship between

228 MOIST THERMODYNAMICS

air ﬂows along a y surface than along say a horizontal surface, or even a topogra-

phical surface.

Equivalent Potential Temperature (

)

We will n ow ﬁnd the equivalent potential temperature for an air parcel undergoing

phase transition. We again assume an adiabatic, reversible system with multiple

phases. Strictly, this is possible only at the triple point temperature, otherwise the

ice and liquid cannot both be in equilibrium with vapor at the same time. Hence, we

will ﬁnd diabatic sources to any e quivalent potential temperature that we deﬁne

when both liquid and ice are present at other than the triple point. Equati on (46)

depicts entro py change for such an irreversible system. Note that there is not a

general condition of equilibrium at any temperature to reduce this equation to an

exact differential. Since entropy is a state variable, the entropy of the ﬁnal state is

determined by the state parameters of the ﬁnal state, which themselves are dependent

on path. Hence we cannot integrate Eq. (46) as we did with (62) to ﬁnd a moist

entropy similar to Eq. (64).

Nevertheless, as previously stated, entropy is an absolute, and according to Eq.

(41), it is a sum of the entropies of each component, which for speciﬁc entropy is

written

s ¼ s

þ r

: ð65Þ

Figure 6 273 K y surface the March, 1993 Storm of the Century. Note that the cold y

surface, ﬂows along the ground like a heavy ﬂuid and even dams up against the mountains.

The wave like feature in the southeastern quadrant are the warm front and cold front created by

the cyclone moving up the east coast at the time of this drawing.

9 ENTROPY VARIABLES FOR MOIST AIR 229

Employing the deﬁnition of speciﬁc entropy we can write

¼ c

ln T  R

ln p

; ð66Þ

¼ c

ln T  R

ln e

; ð67Þ

¼ c

ln T  R

ln e

; ð68Þ

¼ c

ln T  R

ln e

: ð69Þ

where s

is the equilibrium entropy of the liquid surface and s

is the equilibrium

entropy over the ice surface, deﬁned by the entropy of vapor at saturation vapor

pressure as given by the Clausius–Clapeyron equation. The entropies for pure liquid

and ice are, respectively,

¼ c

ln T ð70Þ

¼ c

ln T ð71Þ

Now substituting Eqs. (40), (47), and (66) to (71) into Eq. (65), we obtain an

equation describing the total entropy of a mixed-phase system:

s ¼ðc

þ r

Þ ln T  R

ln p

þ r

 r

: ð72Þ

Although the effects of curvature, solution, chemical changes, and other fairly minor

considerations have been neglected, this equation accurately deﬁnes the total speciﬁc

entropy of a parcel. Under equilibrium conditions, and except for the minor omis-

sions described, we would expect s to be invariant for moist adiabatic processes. We

can readily identify the differential of Eq. (72) within Eq. (46) and so determine the

source of entropy to be

ds ¼ d





 c

: ð73Þ

As expected, the irreversible (diabatic) effect of nonequilibrium is proportional to the

amount of phase transition occurring under nonequilibrium conditions in addition to

external mass ﬂuxes of water and diabatic heat sources. Hence Eq. (73) describes the

change in moist entropy resulting from irreversible processes.

We can now follow the same procedure as we did with Eqs. (61) and (62) to

deﬁne an equivalent potential temperature (y

) for a moist adiabatic process to be

d ln y

 ds ð74Þ

230 MOIST THERMODYNAMICS

where c

¼ c

þ r

. Integrating Eq. (74) and deﬁning the arbitrary constant we

get

ln y

 s þ R

ln P

ð75Þ

Substituting Eq. (72) into Eq. (75), we obtain the expression:

¼ T



ðH

½ðr

þr

ÞR

Þ=c

ðH

r

½l

l

=c

: ð76Þ

Similar to y

for dry adiabatic reversible processes in moist air, y

is conserved for

all moist adiabatic processes carried out at equilibrium. We can relate the changes of

to the irreversible changes in entropy by rewriting Eq. (73) as:

½l

þ R

T ln H

ðdr

 d

ÞR

T ln H

c

T ln Td

ðr

þ r

Þþq

ð77Þ

Note the inclusion of the external derivative for ice. This demonstrates that for the

case of an adiabatic system in equilibrium, and neglect of heat capacity of liquid, y

is conserved.

Note that the more vapor in the air the greater the y

. It is proportional to the

amount of potential energy in the air by the effects of temperature, latent heat, and

even geopotential energy combined. Hence y

tends to be high on humid warm days

and low on cool and=or dry days. It also tends to be greater at high elevations than

low elevations for the same temperature because of the lower pressure present at

higher elevations. The statement: ‘‘The higher the y

is at low levels, the greater the

potential for strong moist convection,’’ is analogous to the statement: ‘‘The higher

the y at low levels, the greater the potential for dry convection.’’ Whereas, we look at

a tank of relatively incompressible water and say warm (cold) water rises (sinks), we

look at the dry atmosphere and say warm (cold) y rises (sinks) and look at the moist

saturated atmosphere and we state warm (cold) y

rises (sinks).

If we ignore diabatic heating effects such as radiation, friction, and heat conduc-

tion at the surface, y

is nearly perfectly conserved in the atmosphere! y

acts like a

tracer such that one can identify an air parcel from its y

and trace where it came

from, even in the midst of moist processes. Figure 7 depicts the 345 K y

surface for

a supercell thunderstorm viewed from the northeast. A thunderstorm occurs when

warm y

builds up under a region of colder y

, creating the condition where the

warm y

air will rise if a cloud forms and the moisture within the warm y

air

condenses. Also, the condition evolves, where the colder y

air at middle levels

will sink if evaporation takes place. Both of these processes are occurring in Figure

7. The rising currents of warm y

air form a ‘‘tree trunk’’-like structure of the 345 K

, very analogous to rising plume in a lava lamp. To the west (right in Fig. 7) rain is

falling into the cold y

air at middle levels where it is evaporating causing the cold y

10 PSEUDO-ADIABATIC PROCESS (y

) 231

air to sink to the surface. The surface, colored according to its temperature, is cold in

the middle of the pool of cold y

air sinking to the ground. The power of using

equivalent potential tem perature to understand the inner str uctures of complex moist

convective weather systems is demonstrated in this ﬁgure. Many other weather

systems evolve from energy released by phase change including tropical cyclones

and some middle latitude cyclones.

10 PSEUDO-ADIABATIC PROCESS (

)

Because entropy is a function of pressure, temperature, and liquid and ice water, a

multiphase process cannot be represented on a two-dimensional thermodynamic

diagram. It is convenient to deﬁne a pseudo-adiabatic process, where the heat

capacity of liquid and ice is neglected.

Omitting the liquid water term (and references to ice) from Eq. (72), and differ-

entiating we can write

¼ðc

þ r

Þd ln T  R

d ln p

þ d



 dðr

ln H

Þð78Þ

Since the ﬁrst term on the RHS now contains r

instead of r

, an exact differential is

not possible. Bolton integrated numerically and derived the following expression for

the pseudo-equivalent potential temperature y

, as:

¼ T



0:2854ð10:28r

exp r

ð1 þ 0:81r

3376

sat

 2:54



ð79Þ

Figure 7 345 K y

surface of a model simulation of supercell thunderstorm observed over

Montana on 2 August, 1981. The view is from the northeast. Generally y

increases with

height, i.e., the warmest air is on top. But summertime and tropical conditions allow warm y

to be produced near the surface creating a situation where plumes of warm y

rise and cold

plumes sink as can be seen in the ﬁgure. The surface plane is colored with surface temperature

where cold air from evaporational cooling is found in the western sector of the storm resulting

from cold evaporating downdrafts carrying cold y

from middle levels to the surface.

232

MOIST THERMODYNAMICS

where T

sat

is a saturation temperature deﬁned as one of:

sat

2840

3:5lnT  ln e  4:805

þ 55; ð80Þ

sat

T  55



lnðH

2840

þ 55: ð81Þ

sat

can also be determined graphically to be the temperat ure of the lowest conden-

sation level (LCL).

The pseudo-adiabatic (y

) isentropes parallel the adiabatic wet-bulb potential

temperature (y

). The y

is related to y

by:

¼ y

exp r

ð1 þ 0:81r

3376

 2:54



; ð82Þ

where

 r

ðp

; y

Þ: ð83Þ

The pseudo-equivalent potential temperature is interpreted as a two-step process

being pseudo-adiabatic ascent to zero pressure followed by dry adiabatic descent to

¼ 1000 mb. This is how we label the moist adiabats on a thermodynamic

diagram.

11 NEGLECTING HEA T STORAGE

A common approximation made to the ﬁrst–second law is to neglect the heat storage

by water. This greatly simpliﬁes the heat capacity and gas constant terms such that

’ c

and R

’ R

. This effectively reduces Eq. (52) to:

d ln T  R

d ln p þ



ð84Þ

Generally the e ffects of this approximation are negligible for meteorological appli-

cations. As a result of this approximation, y

’ y and

’ y exp

 l

LCL

ð85Þ

11 NEGLECTING HEAT STORAGE 233

where T

LCL

is the temperature at the lowest condensation level at which the relative

humidity ðH

Þ is 1. It also follows that:

d ln y 

¼ q

ð86Þ

These approximations are standard in most applications.

12 HYDROSTATIC BALANCE AND HYPSOMETRIC EQUATION

It is sometimes useful to consider the force balance responsible for suspending an air

parcel above the surface. The force upward results from the pressure change across

the parcel per height change, which gives T net force per parcel volume. The down-

ward force per parcel volume is gravity multiplied by parcel density. Setting these

forces equal we obtain the hydrostatic balance:

dp ¼rgdz ð87Þ

where z is the height coordinate.

Strict hydrostatic balance is not adhered to in the atmosphere, otherwise there

would not be vertical acceleration. But the balance is usually very close, and nearly

exact over a time average. Assuming the balance, variations in pressure can be

converted to variations in height.

We can substitute the equation of state for density to obtain the hypsometric

equation:

d ln p

¼

ð88Þ

The hypsometric can be integrated to give

p ¼ p

exp

gDz

ð89Þ

where the subscript 0 refers to an initial value, the Dz is the height change from the

initial value, and the bar represents an average value during the change from the

initial state. This equation is commonly used to ﬁnd the height change between two

pressures or the pressure change between two heights. A common use of this

formula is to ﬁnd the pressure the atmosphere would have at sea level given a

pressure measured at a surface location above sea level.

234 MOIST THERMODYNAMICS

13 DRY AND MOIST ADIABATIC LAPSE RATES ðG

AND G

)

A by-product of assuming hydrostatic balance is that we can determine how

temperature would change with height for different thermodynamic processes. For

an adiabatic process, where dy ¼ 0, it is easily shown that Eq. (88) requires that the

dry lapse rate of temperature (G

)be

¼

¼ 9:8



C=K : ð90Þ

Similar equations can be derived for a moist lapse rate G

occurring in a saturated

(w.r.t. liquid) atmosphere. Then applying Eq. (84) for a no-ice system:

1 þ

; ð91Þ

where r

is the saturation mixing ratio, and where we have assumed that the air

parcel remains at 0% supersaturation. Notice that the moist adiabatic lapse rate is

reduced from the dry adiabatic lapse rate because the latent heating of condensation

counters a portion of the expansional cooling. This effect weakens with decreasing

temperature as the rate of change of saturation mixing ratio with height decreases.

Dry and Moist Static Energy (h and h

)

It is sometimes convenient to work with a thermodynamic variable that is directly

related to enthalpy. Recall that we looked at this in the ﬁrst section where we deﬁned

gravitational potential energy. It is useful to do the same here, further subdividing the

contributing energies. In most applications of static energy, direct measurement of

condensate is not possible and so we cannot consi der the energies stored in the liquid

or ice phases.

The partial work term R

d ln P found in the ﬁrst law is conceptually difﬁcult.

We learned that the term comes from the work performed by expansion that depletes

the parcel of total enthalpy. This can either reduce its temperature or slow it down,

i.e., reduce its kinetic energy. For large-scale ﬂows, we can generally neglect the

effect on the parcel’s kinetic energy and assume a nonaccelerating, hydrostatic

balance. Then we can employ the hydrostatic Eq. (87) and transform R

d ln P

into gdz. Under the hydrostatic assumption, the partial work term is thus shown

to be equivalent to a conversion of enthalpy to geopotential energy.

Ignoring the effects of ice, and diabatic processes, Eq. (87) then is written:

dðc

dT  gdzþ l

Þ¼q: ð92Þ

13 DRY AND MOIST ADIABATIC LAPSE RATES 235